弹体侵彻混凝土的临界跳弹*

段 建,王可慧,周 刚,薛斌杰,初 哲,李 明,戴湘晖,耿宝刚

(西北核技术研究所，陕西 西安 710024)

弹体侵彻混凝土的临界跳弹*

段 建,王可慧,周 刚,薛斌杰,初 哲,李 明,戴湘晖,耿宝刚

(西北核技术研究所，陕西 西安 710024)

为了保证钻地战斗部打击防护层目标时不发生跳弹，需要对弹体侵彻目标的临界跳弹角度进行分析和估算。开展了一定大长径比弹体斜侵彻混凝土的跳弹实验，分析了在250～430 m/s速度下弹体侵彻30和60 MPa钢筋混凝土的临界跳弹角度，给出了弹体临界跳弹角度包络线。当靶板强度相同时，随着侵彻速度的增加，弹体的临界跳弹倾角增大，增大的趋势逐渐变缓；在相同侵彻速度下，随着靶板强度的增加，弹体的临界跳弹倾角减小；经验公式分析得到的弹体临界跳弹倾角偏低于实验，但偏差基本在3°以内。

爆炸力学；跳弹性能；侵彻战斗部；混凝土；临界跳弹角度

钻地战斗部对地下深埋加固目标的有效打击模式是贯穿防护层介质、侵入目标结构内部爆炸，依靠爆炸产生的冲击波和破片等对目标内部的设施和人员进行破坏和毁伤[1]。然而，在实际作战过程中，由于载体作用方式、目标表层特性、弹体的气动性能以及末端制导等因素的影响，战斗部攻击目标时将会有一定的倾角和攻角[2-3]。当战斗部的倾角或攻角大于某一临界角度时，将产生跳弹[4]。

跳弹是弹体在斜侵彻过程中产生的一种特殊现象，就是弹丸侵入或者碰击目标介质后、又从介质表面跳出来并继续在空中运动的现象。弹体一旦跳弹，就失去了对目标的侵彻功能，战斗部侵入不到目标内部，就不能对目标内的设施及人员形成有效打击。因此，为保证战斗部有效侵彻目标，需要对战斗部侵彻目标的临界跳弹角度进行分析和估算，确保战斗部侵彻目标时的角度控制在临界跳弹角度范围以内。一般情况下，弹体的攻角能够控制，而倾角的影响因素多、变化范围大。因此，本文中仅对倾角下的弹体跳弹性能开展研究。

对弹体在倾角下的跳弹研究，相关文献报道主要集中在跳弹现象和数值模拟方面[4-6]，而在实验方面的研究较少。本文中，开展一定大长径比弹体(长径比L/d=8.32)在250～430 m/s速度下侵彻30和60 MPa钢筋混凝土的跳弹实验，分析弹体侵彻钢筋混凝土的临界跳弹角度，结合经验公式分析结果，给出弹体临界跳弹角度包络线，拟为进行战斗部有效作战提供技术指导和依据。

1 实 验

1.1 方案

在130 mm轻气炮上，进行不同倾角下弹体侵彻混凝土靶板实验，研究弹体不同速度下侵彻混凝土靶板的跳弹情况，分析弹体临界跳弹角度。实验原理如图1所示。弹托起定心、闭气的作用。高压气体释放后在膛内形成高压，推动弹托和弹体沿炮膛加速运动，使得弹体以一定的速度撞击斜置的混凝土靶板。调整混凝土靶板的倾斜角度，可以设计不同倾角的弹体撞靶实验，研究弹体产生跳弹的临界角度。

对弹体进行弹托脱壳设计，实现了弹体撞击靶板前的弹、托分离，消除了弹托对弹体撞靶瞬间受力和姿态的影响。脱壳原理如图2所示。弹和弹托向前高速飞行，当弹托接触脱壳器时，脆性材料作为弹托，撞击瞬间发生碎裂，由于弹托结构对称且材料均匀，近似认为破碎沿弹轴对称，可以忽略它对弹体姿态的影响，碎块在气动力的作用下远离弹体。这样，弹体与弹托分离，弹体将在姿态几乎不受干扰的情况下飞行并撞靶。

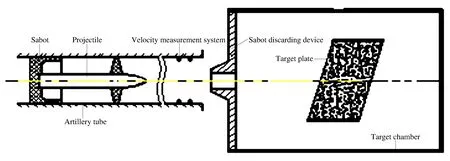
图1 倾角侵彻实验原理示意图Fig.1 Schematics of penetrator impacting targets with oblique angle

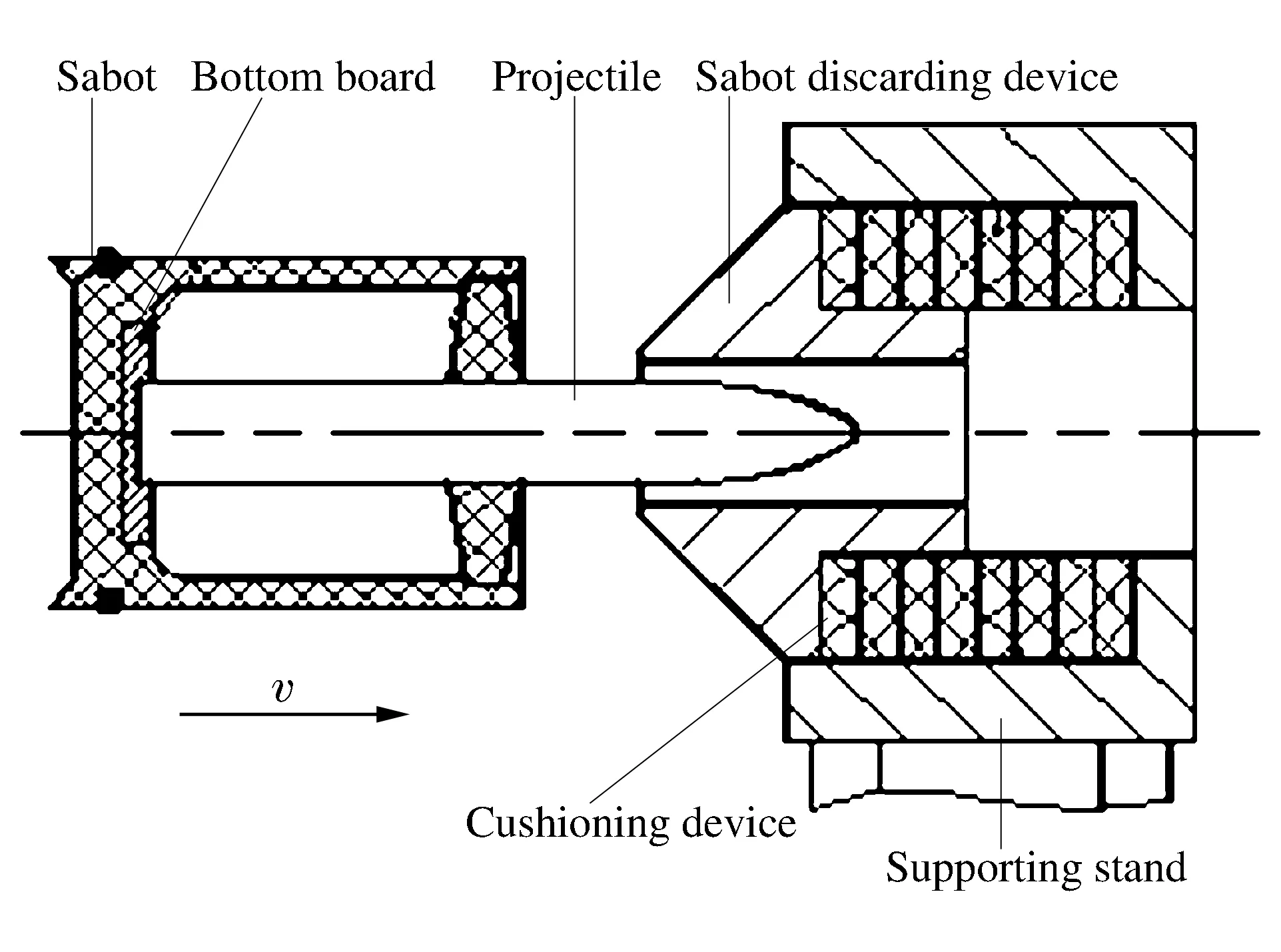
图2 脱壳过程示意图Fig.2 Schematic diagram of sabot discarding

1.2 弹体

小尺寸模拟弹直径为50 mm，长度为416 mm，重量约3.6 kg，弹体内装填模拟装药，如图3所示。弹体材料采用30CrMnSiNi2MoVE高强钢，热处理后的材料力学性能分别为：抗拉强度1 680 MPa，屈服强度1 510 MPa，延伸率14%，冲击功72 J，断裂韧性112 MPa·m1/2。

1.3 靶体

圆柱形钢筋混凝土靶的设计强度为30和60 MPa，体积配筋率为0.2%。靶板直径为1.0 m，厚度为0.7 m，倾角为35°和45°。为减小弹体侵彻过程对混凝土靶边界效应的影响，圆柱靶周围用5 mm厚的钢箍加固，如图4所示。

混凝土靶板制作中，水泥、水和骨料含量依据国军标GJB 1112-91《军用机场场道工程施工及验收规范》。混凝土靶板在标准温度、湿度条件下养护28 d。实验前对加工的钢筋混凝土靶进行强度检测，强度分别为31.5和61.8 MPa。

图3 实验弹体Fig.3 Experimental penetrator

图4 实验用钢筋混凝土靶Fig.4 Experimental reinforced concrete targets

2 结果及分析

2.1 结果

进行了20余发实验弹撞击钢筋混凝土靶板实验，撞靶速度范围为250～430 m/s，撞靶倾角范围为30°～45°。图5给出了弹体分别在约250和420 m/s速度下撞击30 MPa钢筋混凝土靶未跳弹和跳弹情况的典型实验图片。

图5 弹丸侵彻30 MPa钢筋混凝土靶Fig.5 Penetrators impacting 30 MPa reinforced concrete target

弹体侵彻60 MPa钢筋混凝土靶板实验11发，速度约260、310、340、380和420 m/s。约260 m/s速度下的打靶实验3发：第1发实验靶板倾角设计为30°，弹体撞靶速度为258 m/s，弹体撞靶后未发生跳弹，侵入混凝土靶中；根据第1发实验结果，调整靶板倾角至33°，然后进行第2发打靶实验，弹体以254 m/s的速度撞击靶板，由于钢筋的约束，弹体恰好嵌在靶板内部，根据弹道分析，弹体接近临界跳弹；然后继续调整靶板倾角至36°，又进行了第3发打靶实验，弹体在257 m/s速度下撞击靶板，撞靶后弹体明显跳弹，弹体穿入防护钢靶中。约310 m/s速度下的弹体打靶实验2发：第1发实验弹体以308 m/s 速度、35°倾角撞击靶板，撞靶结束后，弹体落入靶箱内，根据弹道分析，弹体未发生跳弹，但由于没有外力约束，实验弹从混凝土靶中滑落；第2发实验弹体以312m/s 速度、38°倾角撞击靶板，撞靶后弹体跳弹，并侵入混凝土靶板上方的防护钢靶中。约340 m/s速度下的弹体打靶实验2发：第1发实验弹体以342 m/s速度、36°倾角撞击靶板，弹体撞击靶板后，未发生跳弹；然后增加弹体撞靶倾角至39°，进行第2发实验，实验弹体以338 m/s 速度、39°倾角撞击靶板，弹体基本处于临界跳弹状态。约380 m/s速度下侵彻钢筋混凝土靶板实验2发：第1发实验弹体撞靶速度为388 m/s，撞靶倾角为40°，撞靶结束后弹体侵入靶中；调整弹体撞靶倾角至42°后进行第2发实验，弹体以383 m/s的速度撞击靶板，发生跳弹。约420 m/s速度下的弹体打靶实验2发：第1发实验弹体以426 m/s速度、43°倾角撞击混凝土靶板，弹体跳弹；第2发实验弹体撞靶倾角设计为42°，弹体以425 m/s速度撞击靶板后发生临界跳弹，并侵入到防护钢靶中。

弹体侵彻30 MPa钢筋混凝土靶板实验10发，速度约260、300、340、380和420 m/s。约260 m/s速度下的实验2发：第1发实验弹体撞靶速度257 m/s、撞靶倾角36°，实验后弹体侵入靶中，弹体在靶中的垂直侵彻深度约11 cm，弹道长度约42 cm；第2发实验弹体撞靶速度256 m/s、撞靶倾角40°，实验后弹体明显跳弹。约300 m/s速度下的实验2发：第1发实验的弹体撞靶速度和撞靶倾角分别为304 m/s和38°，实验后弹体侵入靶中；第2发实验的弹体撞靶速度和倾角为302 m/s和41°，实验后弹体跳弹，落入靶箱中。约340 m/s速度下的实验2发：第1发实验弹体以343 m/s速度、39°倾角撞击靶板后，弹体侵入靶板中，未发生跳弹；调整撞靶角度进行第2发实验，弹体以342 m/s速度、42°倾角撞击靶板，弹体跳弹。约380 m/s速度下的实验2发：第1发弹体以377 m/s速度、41°倾角撞击靶板后，未产生跳弹；第2发弹体以379 m/s速度、44°倾角撞击靶板后，发生跳弹。约420m/s速度下的实验2发：第1发实验弹体撞靶速度432 m/s、撞靶倾角42°，撞靶后弹体滞留在靶板内，弹轴与水平方向夹角65°；第2发实验弹体撞靶速度417 m/s、撞靶倾角45°，实验后弹体跳弹，落入靶箱内。

2.2 分析

2.2.1 实验结果分析

如果每隔1°进行一次弹体侵彻实验，直至相邻两发实验有跳弹和未跳弹情况出现，这样，可以把弹体临界跳弹角度控制在1°范围以内。但是，这样需进行大量的实验。可通过对弹体侵彻靶板弹道分析，如果能够在2°～3°范围内近似给出每组实验下的弹体临界跳弹角度，然后进行数据拟合，根据拟合曲线，可近似分析出弹体的临界跳弹角度。

通过对上述实验结果及弹体侵彻弹道综合分析，可分别得到弹体侵彻60和30 MPa钢筋混凝土靶的临界跳弹角度。在260、310、340、380和420 m/s速度下，弹体侵彻60 MPa钢筋混凝土的临界跳弹倾角角度分别约为34°、37°、39°、41°和42°。在260、300、340、380和420 m/s速度下，弹体侵彻30 MPa钢筋混凝土的临界跳弹倾角角度分别约为38°、40°、42°、43°和44°。

2.2.2 经验结果分析

采用球形空腔理论模型[7]，对弹体斜侵彻靶板过程进行了受力分析，并开展了大量不同尺寸缩比弹在200～860 m/s速度下的侵彻实验(实验数量近百发)。结合实验结果，拟合给出了弹丸末端姿态角ζ与初始倾角β和侵彻能力参数P′的半经验公式：

ζ=c0βc1P′c2

(1)

P′=P/d

(2)

式中：c0、c1和c2是量纲一系数，c0=e1.27，c1=0.99，c2=-0.26；d为弹体直径(m)；P为弹体侵彻深度(m)；P′为量纲一参量，定义为弹体侵彻能力准数；β为初始倾角(弹体速度方向与靶面法向的夹角)；ζ为弹体姿态角(弹体轴线与靶面法向的夹角)。其中P由Young方程计算求得。

Young方程是由C.W.Young[8-11]在3 000多次实验的基础上统计分析得到、用来预估钻地弹侵彻深度的经验方程。Young方程的具体形式如下：

(3)

式中：m为弹体质量(kg)；A为弹体横截面积(m2)；S为可侵彻性指标，与混凝土的配筋率、强度等参数有关；N为弹头形状影响系数；K为侵彻修正系数，与弹体质量有关。

研究表明，在一定速度范围内，当弹体侵彻靶板过程中的末端弹体姿态角大于70°时，弹体开始发生跳弹。可确定当姿态角ζ为70°对应的初始倾角β，作为弹体临界跳弹倾角。根据上述公式，可计算出不同速度下弹体分别侵彻30和60 MPa钢筋混凝土的临界跳弹倾角。

2.2.3 结果对比分析

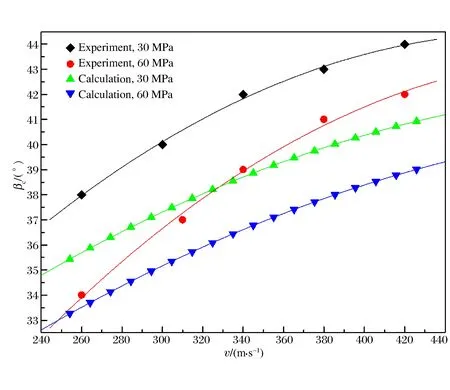
图6 弹体临界跳弹倾角角度与速度关系曲线Fig.6 Relation curves of projectile’s critical ricochet oblique angles and penetration velocities

根据实验和计算分析得到，弹体在250～430 m/s速度下分别侵彻30和60 MPa钢筋混凝土靶的临界跳弹角度，如图6所示。

相对于实验结果，经验公式计算得到的弹体的临界跳弹倾角角度偏低，但偏差不超过3°，且实验结果与经验分析结果的临界跳弹角度变化趋势基本一致。随着侵彻速度的增加，弹体的临界跳弹角度变大，且弹体临界跳弹角度随速度增加而增大的变化趋势逐渐变缓。这说明随速度的增加，弹体临界跳弹角度存在上限。可以想象，在不考虑弹体结构强度情况下，其临界跳弹角度上限为90°，弹体轴线与靶面平行。此种情况下，无论速度多高，弹体都不会对目标进行侵彻，也就是说弹体发生了跳弹。

3 结 论

采用实验和经验分析的方法，对长径比为8.32的弹体在250～430 m/s速度下分别侵彻30和60 MPa钢筋混凝土靶的临界跳弹角度进行了研究，结论如下。

(1)弹体侵彻相同强度靶板，随着侵彻速度的增加，弹体的临界跳弹倾角角度变大，且弹体临界跳弹倾角角度随速度增加而增大的变化趋势逐渐变缓。

(2)弹体在相同速度下侵彻不同强度靶板，随着靶板强度的增加，弹体的临界跳弹倾角角度变小。

(3)实验分析得到的弹体在250～430 m/s速度下侵彻30 MPa钢筋混凝土的临界跳弹角度范围为38°～44°，侵彻60 MPa钢筋混凝土的临界跳弹角度范围为34°～42°；经验公式分析得到的弹体在250～430 m/s速度下侵彻30 MPa钢筋混凝土的临界跳弹角度范围为36°～41°，侵彻60 MPa钢筋混凝土的临界跳弹角度范围为34°～39°；经验公式分析得到的弹体临界跳弹角度结果偏低于实验结果，但偏差基本在3°以内。

(4)实验结果与经验分析结果有一定的偏差，且实验得到的弹体临界跳弹角度结果大于经验分析结果，分析造成这一差别的原因如下：实验所采用的靶板为钢筋混凝土靶，靶板中的钢筋对弹体侵彻过程弹道偏转有约束作用，可抑制弹体发生跳弹，从而提高了弹体的临界跳弹角度；而经验公式是根据弹体侵彻素混凝土靶(靶中无配筋)实验结果建立的，相对于钢筋混凝土靶，素混凝土靶中无钢筋对弹体侵彻过程的偏转进行约束，导致弹体侵彻素混凝土靶的临界跳弹角度小些。因此，经验公式适合于弹体侵彻素混凝土靶的临界跳弹分析，而对于弹体侵彻钢筋混凝土靶的临界跳弹分析，实验结果更接近实际。

结合实验和经验公式分析结果，可对弹体侵彻混凝土靶的临界跳弹角度进行计算、分析，给出弹体有效侵彻靶板目标的角度范围，为进行战斗部作战指导提供技术依据。

[1] Kanchibotla S. Modeling fines in blast fragmentation and its impact on crushing and grinding[C]∥A Conference on Rock Breaking. Kalgoorlie, Australia, 1999:37-44.

[2] Goldsmith W. Non-ideal projectile impact on targets[J]. International Journal of Impact Engineering, 1999,22(2/3):95-395.

[3] Frew D J, Forrestal M J, Hanchak S J. Penetration experiments with limestone targets and ogive-nose steel projectiles[J]. Journal of Applied Mechanics, 2000,67(4):841-845.

[4] Lee W, Lee H J, Shin H. Ricochet of a tungsten heavy alloy long-rod projectile from deformable steel plates[J]. Physics of Journal D: Applied Physicss, 2002,35(20):2676-2686.

[5] 刘晋.跳弹机理研究与数值模拟[D].太原:中北大学,2011.

[6] 吴荣波,陈智刚,王庆华.入射角对跳弹现象影响的数值模拟[J].设计与研究,2011,38(10):18-21. Wu Rongbo, Chen Zhigang, Wang Qinghua. Numerical simulation on the impact effect of incidence angle impacting ricochet[J]. Design and Research, 2011,38(10):18-21.

[7] Forrestal M J, Tzou D Y. A spherical cavity-expansion penetration model for concrete targets[J]. International of Solid Structures, 1997,34(31):4127-4146.

[8] Young C W. Depth prediction for earth-penetrating projectiles[J]. International of the Soil Mechanics and Foundations Division, 1969,95(3):803-817.

[9] Young C W. Development of empirical equation for predicting depth of an earth penetrating projectile[R]. SC-DR-67-60, 1967.

[10] Young C W. Equation for predicting earth penetration by projectiles: An update[R]. SAND-88-0013, 1988.

[11] Young C W. Penetration equations[R]. SAND-97-2426, 1997.

(责任编辑 丁 峰)

Critical ricochet performance of penetrator impacting concrete targets

Duan Jian, Wang Kehui, Zhou Gang, Xue Binjie,Chu Zhe, Li Ming, Dai Xianghui, Geng Baogang

(NorthwestInstituteofNuclearTechnology,Xi’an710024,Shaanxi,China)

The critical ricochet angle of a penetrator impacting hard targets obliquely needs to be analyzed and estimated to ensure that no ricochet occur while the penetrator hits the targets. In this work the experiments on the ricochet performance of the penetrator with a big length-to-diameter ratio impacting reinforced concrete targets at a velocity of 250-430 m/s were conducted, the critical ricochet angles in which it impacts the reinforced concrete targets possessing a compressive strength of 30 MPa and 60 MPa respectively were analyzed and estimated, and the envelope curves of the critical ricochet angle were obtained. The results show that, when the intensity of the target is maintained the same, the projectile’s critical ricochet angle increases with the increase of the penetration velocity. This increase gradually slows down. At the same penetration velocity, with the increase of the targets’ strength, the projectile’s critical ricochet angle decreases. The projectile’s critical ricochet angles from the analysis of the empirical formula were lower than those from the experiments, but the deviation is less than 3°.

mechanics of explosion; ricochet performance; penetrating warhead; concrete target; critical ricochet angle

10.11883/1001-1455(2016)06-0797-06

2015-04-17； < class="emphasis_bold">修回日期：2015-07-21

2015-07-21

段 建(1979— )，男，博士研究生，副研究员，duanjian@nint.ac.cn。

O385 <国标学科代码：1303530 class="emphasis_bold"> 国标学科代码：1303530 文献标志码：A国标学科代码：1303530

A