基于荷载时程分析法的钢板混凝土结构墙的抗冲击性能敏感性分析*

朱秀云,林 皋,潘 蓉,路 雨

(1.大连理工大学海岸与近海国家重点实验室抗震分室，辽宁 大连 116024；2.环境保护部核与辐射安全中心厂址与土建部,北京 100082)

基于荷载时程分析法的钢板混凝土结构墙的抗冲击性能敏感性分析*

朱秀云1,2,林 皋1,潘 蓉2,路 雨2

(1.大连理工大学海岸与近海国家重点实验室抗震分室，辽宁 大连 116024；2.环境保护部核与辐射安全中心厂址与土建部,北京 100082)

选取由表面钢板、拉结筋、剪力钉及混凝土组成的钢板混凝土结构墙为研究对象，运用经典显式非线性动力分析软件ANSYS/LS-DYNA，基于荷载时程分析法进行了一系列影响钢板混凝土结构墙抗冲击性能的参数敏感性分析。这些参数包括：墙体厚度、钢板厚度、拉结筋直径与间距等。分析结果表明，以上参数均会影响墙体的抗冲击性能，尤其是墙体与钢板的厚度以及拉结筋的间距。本文的研究工作对于核电厂核岛厂房钢板混凝土结构外墙的设计具有一定的指导与参考意义。

固体力学；抗冲击性能；荷载时程分析法；钢板混凝土结构墙；敏感性分析

9.11事件后，核电厂在大型商用飞机撞击下的安全问题成为公众的焦点。在美国, 将大型商用飞机撞击作为核电厂一种超设计基准事件，以美国联邦法规的新条款10CFR50.150[1]形式颁布, 要求新设计的核动力堆需就抵御大型商用飞机恶意撞击进行专门的评价。其中，文件NEI07-13[2]提供了美国电力研究院发展的一套评价大型商用飞机撞击的方法，对于构筑物整体破坏的评估，推荐了荷载时程分析法和飞射物-靶体相互作用分析法。在我国，核安全法规中还没有针对核电厂抗大型商用飞机撞击评估提出相关要求，但从国际核行业安全评价的发展趋势看，掌握和发展核电厂构筑物抵御大型商用飞机撞击技术，建立和完善相关法规，具有重大意义。

关于钢板混凝土结构与钢筋混凝土结构的抗冲击性能对比，日本Kobori综合研究所分别对1/7.5缩尺飞机模型垂直撞击不同厚度钢筋混凝土(RC)墙[3]及钢板混凝土(SC)墙[4]进行了实验研究；M.Sadiq等[5]和朱秀云等[6]基于非线性有限元软件ANSYS/LS-DYNA对以上实验分别进行了飞射物-靶体相互作用分析法和荷载时程分析法的有限元数值模拟，并对不同厚度的钢筋混凝土(RC)墙与钢板混凝土(SC)墙的抗冲击性能进行了一系列的对比分析，其结论是钢板混凝土结构墙的抗冲击性能优于钢筋混凝土结构墙，尤其是背面钢板能够有效地约束混凝土在撞击方向上的运动，并限制混凝土碎片的飞溅，因此，用于抗飞机撞击的钢板混凝土结构墙体的厚度可以较钢筋混凝土结构适当减薄。针对大型商用飞机恶意撞击事件的补充考虑，美国西屋公司将AP1000屏蔽厂房结构类型由美国核管会批准的DCD第15版钢筋混凝土结构变更为DCD第16版的钢板混凝土结构；国内新设计的大型先进压水堆CAP1400为了抵抗大型商用飞机的撞击，同样将屏蔽厂房设计为钢板混凝土结构。当然，潘蓉等[7]指出钢板混凝土结构由于钢板暴露在外，没有混凝土面层的保护，受火时比钢筋混凝土结构更易于受到影响而丧失强度，需要进一步研究其防火方法。所以在抗商用飞机撞击分析中，一般只允许钢板混凝土结构墙体发生少量变形，不允许被穿透以防止飞机燃油燃烧对钢板混凝土结构墙体造成破坏影响。

为了探讨影响钢板混凝土结构墙体抗冲击性能的参数，本文中基于非线性有限元动力分析软件ANSYS/LS-DYNA[8]，采用HAD101/04《核电厂厂址选择的外部人为事件》[9]提供的波音707-320撞击荷载函数，进行一系列影响钢板混凝土结构墙体抗冲击性能的参数敏感性研究，其参数包括：混凝土厚度、钢板厚度、拉结筋直径与间距等。

1 撞击荷载时程函数

对于荷载时程分析法，首先是确定飞机撞击荷载时程函数。撞击荷载选用导则HAD101/04《核电厂厂址选择的外部人为事件》[9]附录I中列出的波音707-320在典型起落速度370 km/h的荷载时程曲线，如图1所示；撞击面积时程曲线，如图2所示。可考虑2种不同的均布荷载时间函数加载模式。第1种模式是根据商用飞机的特征，其撞击作用分为机身和机翼部分，其机身和机翼的撞击荷载及撞击面积时程曲线分别如图3～4所示；由此相同时刻对应的撞击荷载除以撞击面积，可得到分别作用于墙体的机身与机翼区域的均布荷载时程曲线，如图5所示。第2种模式是如图1～2所示的撞击荷载和撞击面积时程，两者直接相除得到作用于墙体整个飞机区域的一致均布荷载时间函数曲线，如图6所示。

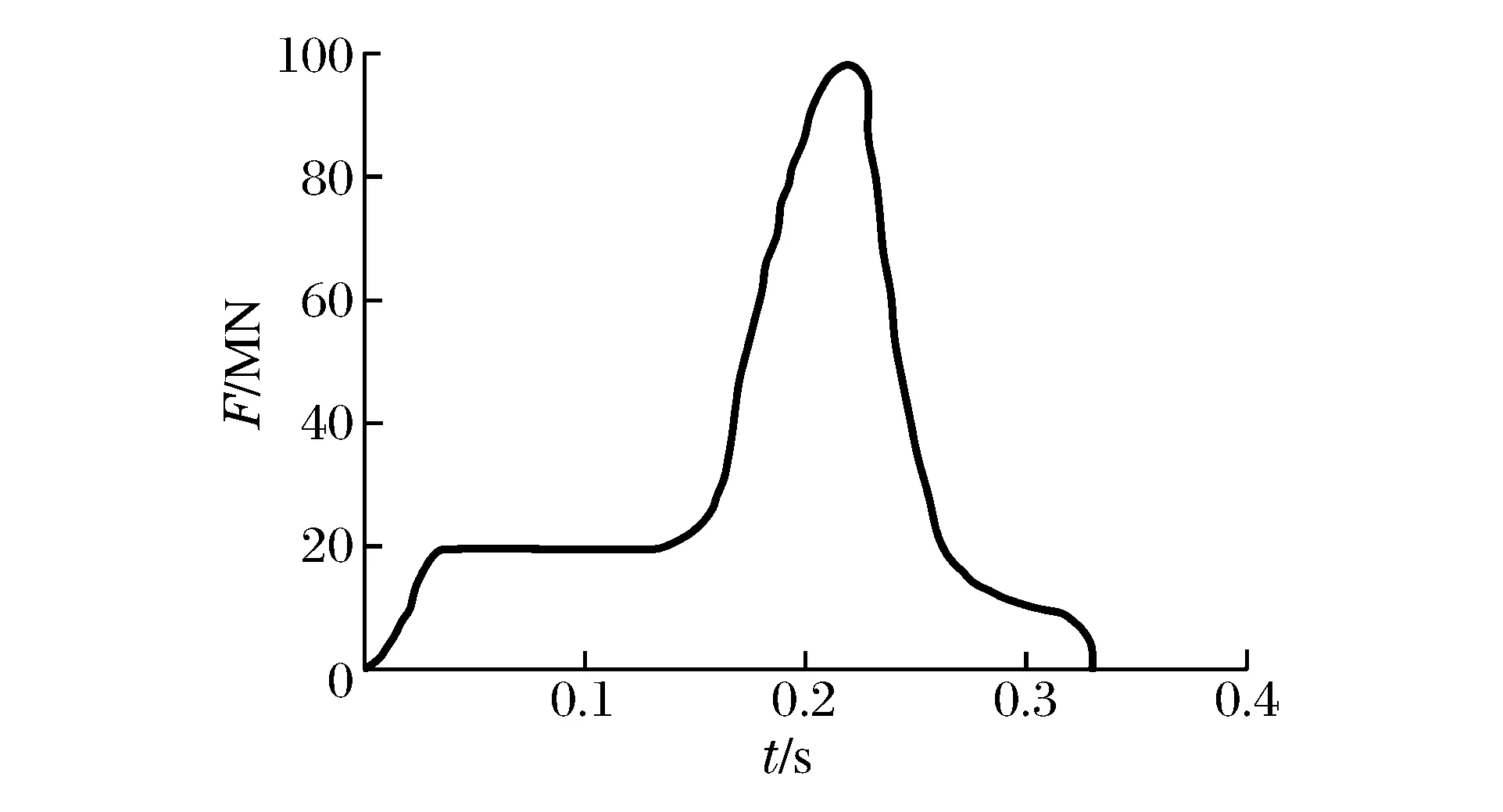
图1 波音707-320的撞击荷载时程曲线Fig.1 Curve of impact force vs. time-history

图2 波音707-320的撞击面积时程曲线Fig.2 Curve of impact area vs. time-history

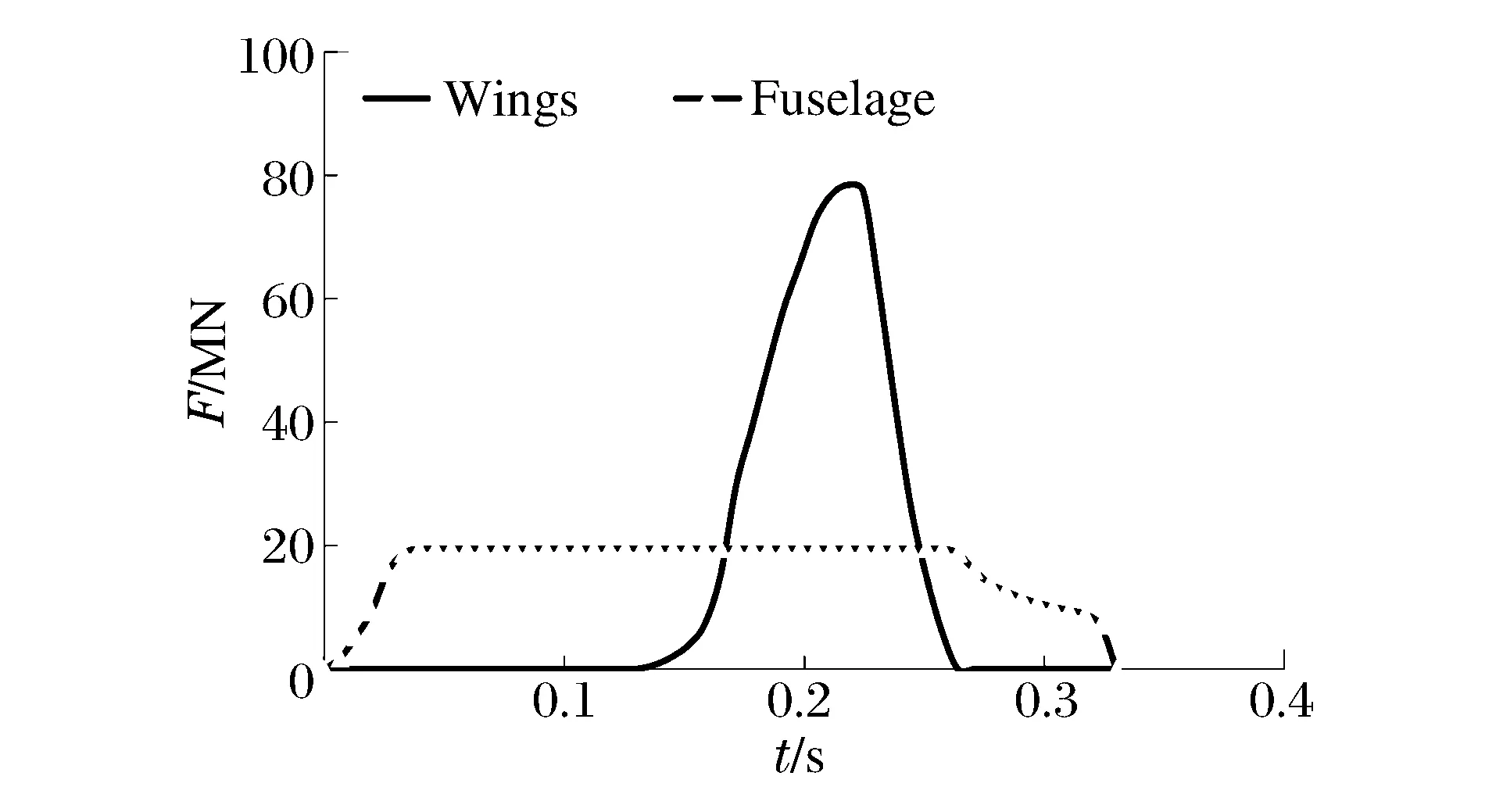
图3 机身和机翼的撞击荷载时程曲线Fig.3 Curves of impact force vs. time-historyfor fuselage and wings

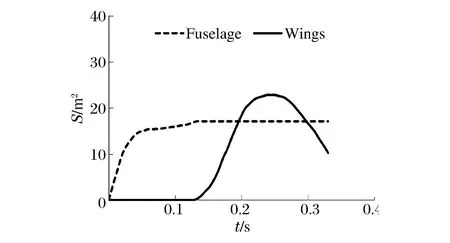
图4 机身和机翼的撞击面积时程曲线Fig.4 Curves of impact area vs. time-historyfor fuselage and wings

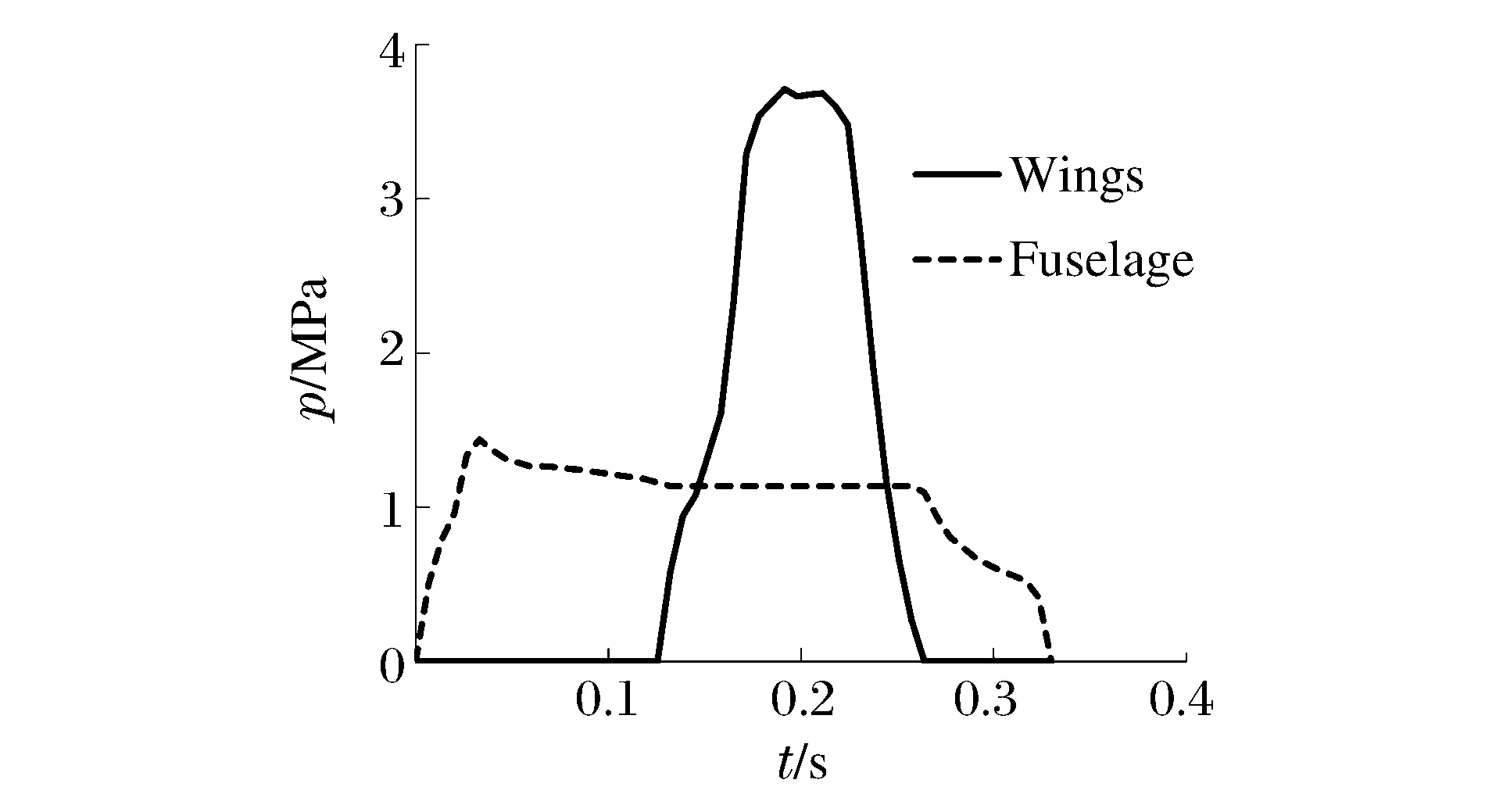
图5 波音707-320机身和机翼的均布荷载时程曲线Fig.5 Curves of evenly distributed impact pressure vs. time-history for fuselage and wings of Boeing 707-320

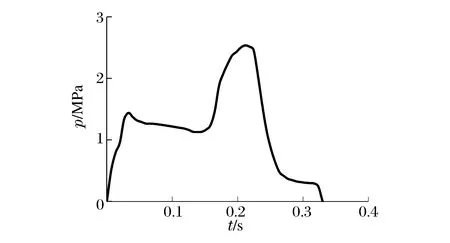
图6 波音707-320整个飞机的均布荷载时程曲线Fig.6 Curve of evenly distributed impact pressure vs. time-history for the whole aircraft of Boeing 707-320

2 数值分析模型

2.1 钢板混凝土结构墙的有限元模型

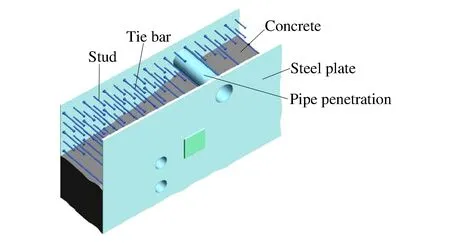
图7 典型的钢板混凝土结构墙示意图Fig.7 Schematic illustration of the typical steel plate concrete (SC) wall

钢板混凝土结构(SC)墙一般由表面钢板、拉结筋、剪力钉以及混凝土等部分组成，其典型的结构形式示意如图7所示。

研究对象为长36 m、高10 m、4个侧立面固定约束的钢板混凝土结构墙体，厚度为0.75～1.0 m，内外层钢板厚12～20 mm，剪力钉直径12 mm、长15 cm，剪力钉间距0.2～0.3 m，拉结筋直径12～20 mm，拉结筋长度与墙体厚度一致，拉结筋间距为剪力钉间距的2倍。通过改变上述参数，进行钢板混凝土墙抗撞击性能的敏感性分析。

钢板混凝土结构墙体的钢板、拉结筋、剪力钉和混凝土分离建模。混凝土、钢板的单元类型分别为solid 164、shell 163，拉结筋和剪力钉的单元类型为beam 161，各个部件的有限元模型如图8所示。混凝土沿墙体的厚度共划分为5层单元，墙体中心区域单元长度约0.2 m，墙体边缘单元长度约为0.4 m，从中间区域向外侧网格渐变；钢板的网格尺寸与剪力钉的间距保持一致，整个墙体模型的单元数为50 721，节点数为70 687。拉结筋、剪力钉及钢板与混凝土之间的连接通过ANSYS/LS-DYNA软件中自带的耦合约束*CONSTRAINED_LAGRANGE_IN_SOLID[8]。撞击荷载作用于墙体中心区域的钢板上，加载区域如图8(b)所示。为有效传递荷载，钢板部件与混凝土部件之间定义为自动面-面接触。

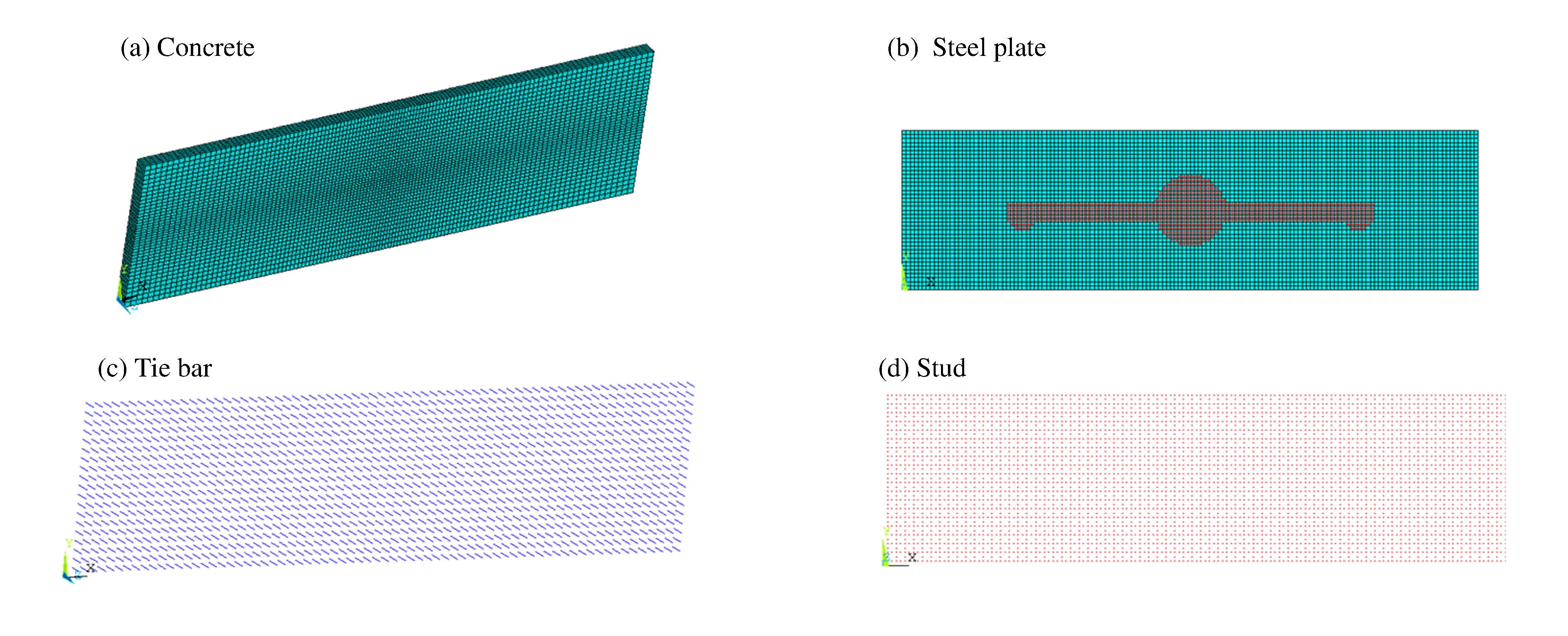
图8 钢板混凝土结构墙的有限元模型Fig.8 FEM model of the steel plate concrete wall

在高速碰撞过程中，钢材和混凝土的强度会随着材料的高应变率有所提高，采用NEI07-13报告[2]中推荐的动力强化系数来考虑此特性。考虑动力强化系数后钢板混凝土结构墙的基本材料参数见表1。表中，ρ为材料密度，E为弹性模量，υ为泊松比，fc为抗压强度,ft为抗拉强度。

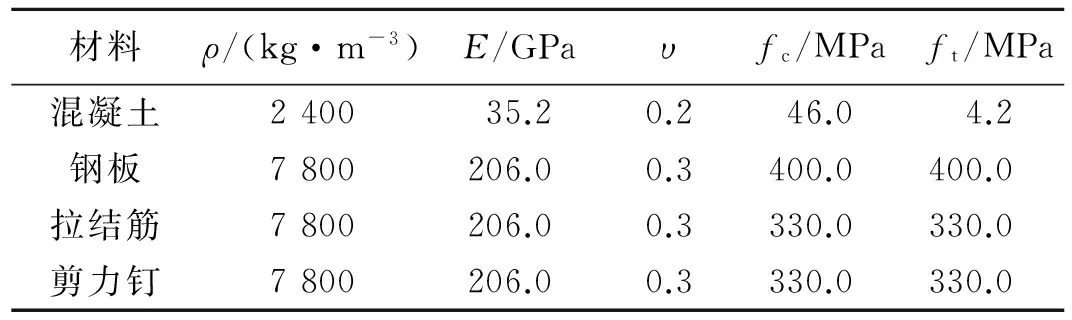
表1 钢板混凝土墙的材料参数Table 1 Material parameters of steel plate concrete wall

2.2 钢板混凝土结构墙的本构模型

2.2.1 钢板、拉结筋及剪力钉材料

由于金属材料在碰撞时材料应变率效应十分明显，故选用考虑屈服、强化及应变率效应的Cowper-Symonds本构模型，该模型为碰撞分析中常用的金属本构。在ANSYS/LS-DYNA软件中Cowper-Symonds本构模型对应于*MAT_PLASTIC_KINEMATIC[8]，其屈服函数为：

(1)

2.2.2 混凝土材料

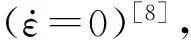
(2)

式中：I1为应力张量第一不变量；J2、J3分别为应力偏张量第二不变量、应力偏张量第三不变量：

(3)

(4)

式中：参数a、b、k1、k2均是混凝土抗拉强度与抗压强度比值(ft/fc)的函数。

通过关键字*MAT_ADD_EROSION[8]控制材料失效，由于冲击荷载作用下，混凝土材料强度会随应变率变化，且在冲击作用下混凝土主要是受压破坏，因此选取主应变作为混凝土材料失效准则。

2.3 数值分析方法的验证

钢板混凝土结构材料本构模型、失效准则以及荷载时程分析方法的合理性验证工作主要基于日本Kobori综合研究所对1/7.5缩尺飞机模型垂直撞击不同厚度钢板混凝土(SC)墙的实验研究[4]。文献[6]中将荷载时程分析法的计算结果与飞射物-靶体相互作用方法计算结果[5,15-16]以及实验结果[4]进行了对比分析，结果表明，荷载时程分析法能够较好地模拟此冲击实验，且计算结果略偏大，验证了钢板混凝土结构墙材料本构模型选取的有效性，以及由于靶体完全刚性假设造成的此方法具有一定的保守性。

3 数值分析结果

基于荷载时程分析法进行一系列影响钢板混凝土墙体抗冲击性能的参数敏感性分析，其中参数包括混凝土厚度(0.75、0.80、0.85、0.90、1.0 m)，钢板厚度(12、14、16、18、20 mm)，拉结筋直径(12、16、18、20 mm)，拉结筋间距(0.4、0.5、0.6 m)。

3.1 不同加载模式的对比分析

为了对比如图5～6所示的2种不同加载模式的保守性，选取钢板厚度为16 mm、拉结筋直径为12 mm、拉结筋间距为0.5 m、墙体厚度为0.90 m的钢板混凝土结构墙为研究对象，进行2种加载模式下的墙体冲击响应对比分析，其墙体背部的最大位移时程曲线与撞击区域混凝土的最大塑性应变时程曲线如图9～10所示。其中，图例“Load case 1”、“Load case 2”分别表示如图5～6所示的加载模式。此外，2种不同的加载模式下混凝土的最大塑性应变云图见图11。

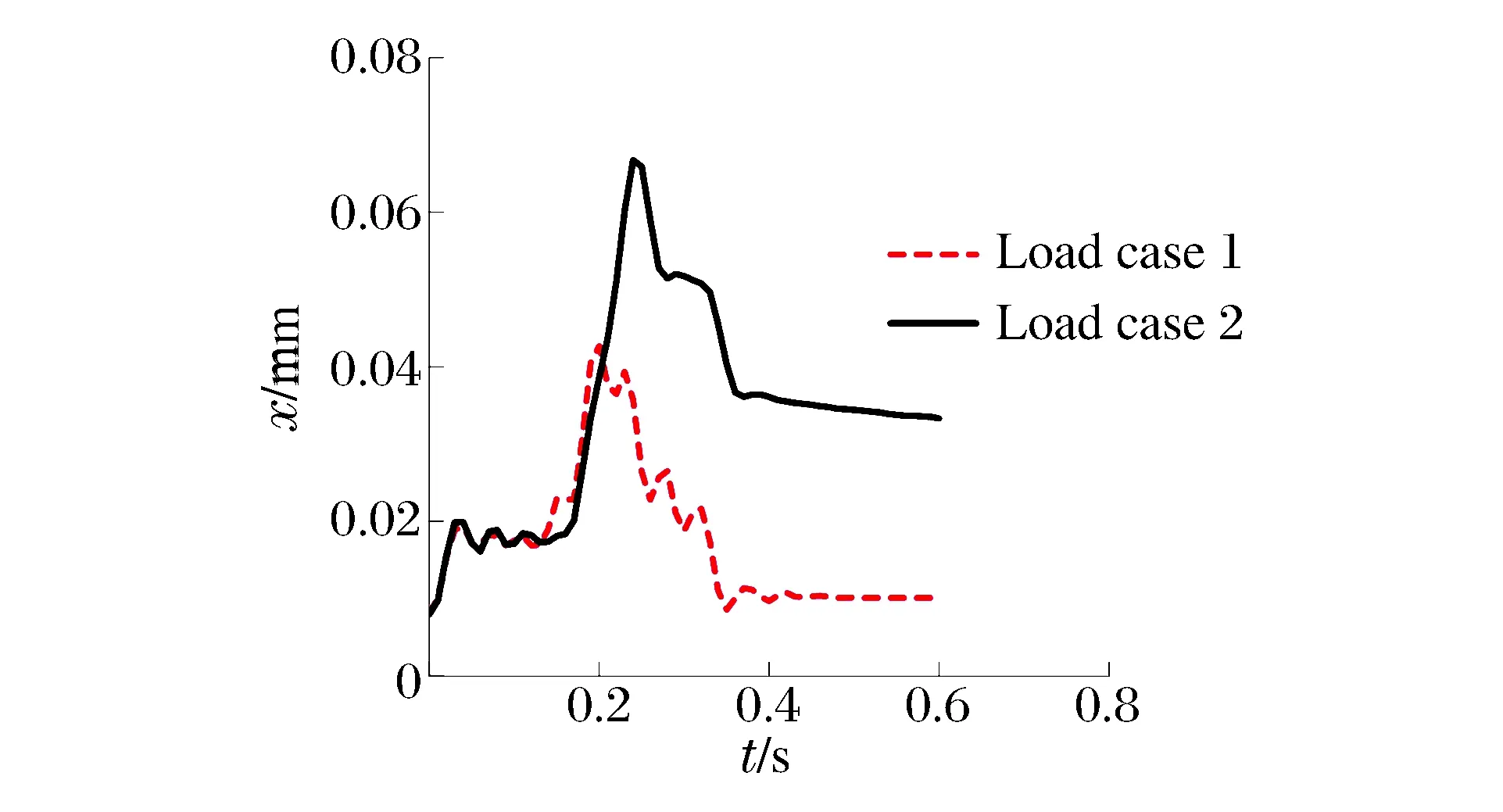
图9 不同加载模式的墙体最大位移时程曲线Fig.9 Curves of max displacement vs. time-historyof SC wall for different loads

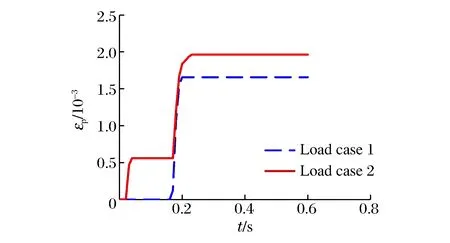
图10 不同加载模式的混凝土最大塑性应变时程曲线Fig.10 Curves of max plastic strain vs. time-historyof concrete for different loads

图11 不同加载模式下混凝土的最大塑性应变云图Fig.11 Contour plot of max plastic strain of concrete for different loads

由图11可见，在不同的加载模式下，其撞击区域混凝土的塑性分布是不同的。第1种加载方式即机身和机翼区域分别加载，由于作用于机翼区域的荷载值远大于机身区域，导致机翼区域的混凝土进入塑性区；而第2种加载方式，即整个飞机撞击区域一致均布加载，则混凝土的塑性区集中于机身及机翼的根部区域。由图9～10中的曲线对比可见，第2种加载模式下墙体的位移响应值和撞击区域混凝土的塑性应变值均比第1种加载模式下的响应值偏大。可见，对于墙体的整体破坏效应评估，其作用于整个撞击区域的较长持时的一致均布加载比单独作用于机身和机翼区域的加载起控制作用。综上所述，鉴于第2种加载模式的保守性，在下文的墙体参数敏感性分析中均采用此整个撞击区域一致均布加载的模式。

3.2 不同钢板混凝土墙厚度的敏感性分析

对钢板厚度16 mm，拉结筋直径12 mm，拉结筋间距0.5 m，墙体厚度分别选0.75、0.80、0.85、0.90、1.00 m的钢板混凝土结构墙体进行抗冲击性能的对比分析。在如图6所示的冲击荷载作用下，以上不同厚度墙体背部的撞击区域处节点沿冲击方向的最大位移时程曲线和撞击区域混凝土的最大塑性应变时程曲线分别如图12～13所示。

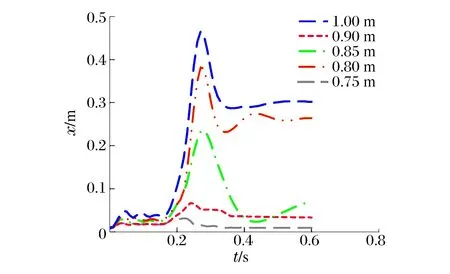
图12 不同厚度SC墙体的最大位移时程曲线Fig.12 Curves of max displacement vs. time-historyfor SC wall with different thickness

图13 不同厚度SC墙体的混凝土最大塑性应变时程曲线Fig.13 Curves of max plastic strain vs. time-historyfor concrete of SC wall with different thickness

从图12～13可见，厚度为0.75、0.80、0.85、0.90、1.0 m的墙体，背部撞击区域的最大位移值分别为46.5、38.2、23.6、6.67、3.13 cm；撞击区域混凝土的最大塑性应变值分别为1.0×10-2、3.68×10-3、2.84×10-3、1.96×10-3、1.24×10-3。可见，墙体厚度对位移响应起到显著的控制作用。比如，墙体厚度从0.8 m增大到0.85 m时，最大位移响应由38.2 cm减小为23.6 cm，相当于减少了38.2%；当墙体厚度从0.8 m增大到0.9 m时，最大位移响应由38.2 cm减为6.67 cm，相当于减少了82.5%；当墙体厚度从0.9 m增大到1.0 m时，最大位移响应由6.67 cm减为3.13 cm。从以上位移对比可得，墙体厚度对于减少位移响应起到显著的控制作用，但当墙体厚度达到一定值(比如0.9 m)，其结构的响应已经较小时，再进一步增大截面的厚度，对于减小位移响应影响不是很显著。同样，当墙体厚度为0.75 m时，撞击区域混凝土的塑性应变达到1.0%，当墙体厚度为0.8 m时，混凝土的塑性应变骤减至3.68×10-3，随着墙体厚度的增大，撞击区域混凝土的塑性应变随之减少。所以，在其他参数不变的情况下，增大墙体的厚度能够非常有效地减小冲击作用下结构的响应。

3.3 不同钢板厚度的敏感性分析

3.3.1 厚度为0.85 m墙的对比分析

对墙体厚度为0.85 m，拉结筋直径为12 mm、间距0.5 m，钢板厚度分别取14、16、18和20 mm的钢板混凝土结构墙，进行墙体的抗冲击性能对比分析。

墙体背部撞击部位区域沿冲击方向的最大位移时程曲线与混凝土的最大塑性应变时程曲线分别见图14～15。从图中可见，随着钢板厚度的增大，墙体背部的最大位移响应以及混凝土的最大塑性应变是减小的；对应钢板厚度为14、16、18和20 mm，其最大位移值分别为24.4、23.6、21.7和19.8 cm，但墙体背部钢板的最终残余位移值相当，可见增大钢板的厚度，可以减小冲击作用下结构的位移响应；撞击区域混凝土的最大塑性应变值分别为2.73×10-3、2.71×10-3、2.65×10-3和2.63×10-3，可见随着钢板厚度的增加，撞击区域混凝土的最大塑性应变值有所减小，但效果并不显著。

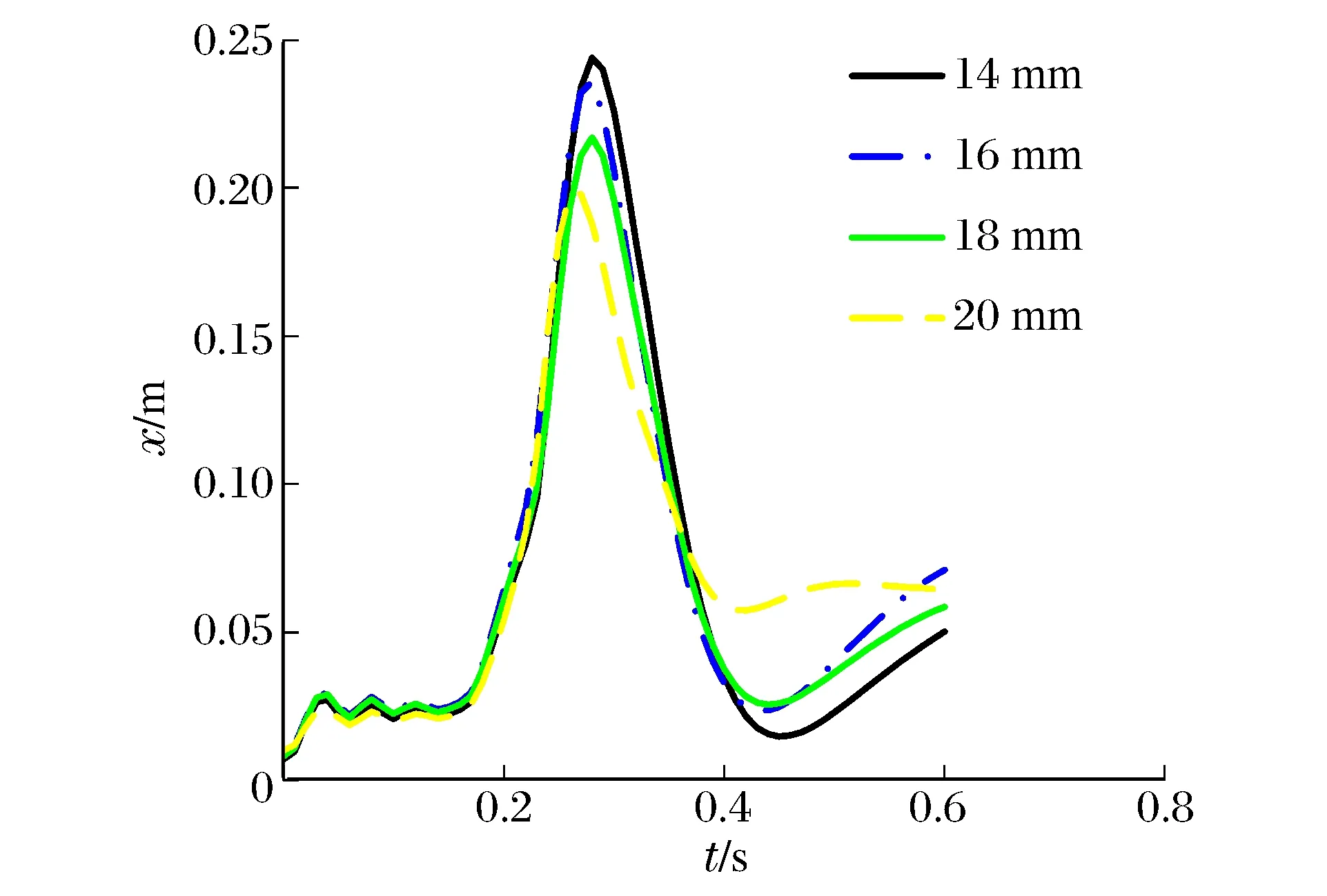
图14 不同钢板厚度的墙体最大位移时程曲线Fig.14 Curves of max displacement vs. time-historyfor SC wall of steel plates with different thickness

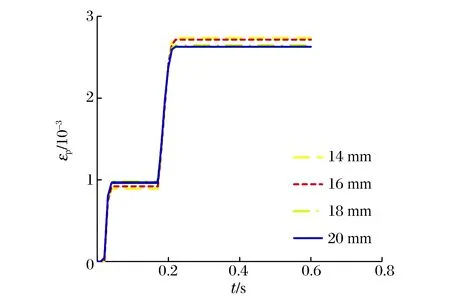
图15 不同钢板厚度的混凝土最大塑性应变时程曲线Fig.15 Curves of max plastic strain vs. time-historyfor concrete for steel plates with different thickness

3.3.2 厚度为0.80 m墙的对比分析

对墙体厚度为0.80 m，拉结筋直径为12 mm、间距为0.5 m，钢板厚度分别为12、14、18和22 mm的钢板混凝土结构墙进行冲击响应的对比分析。

撞击区域墙体背部沿冲击方向的最大位移时程曲线以及混凝土的最大塑性应变时程曲线分别见图16～17。从图中可见，随着钢板厚度的增大，墙体背部的最大位移响应值、最终残余位移值以及混凝土的最大塑性应变均是减小的。钢板厚度为12、14、18和22 mm的墙体，其最大位移值分别为44.8、39.3、31.3和27.0 cm，背部钢板的残余位移值分别为34.3、27.6、15.8、10.0 cm；撞击区域混凝土的最大塑性应变值分别为3.05×10-3、2.84×10-3、2.60×10-3和2.51×10-3。可见，对于相对较薄的钢板混凝土结构墙，增大钢板的厚度，可以有效地减小冲击作用下墙体的位移响应值，以14 mm厚钢板为基准，18、22 mm厚度的钢板墙的最大位移分别减少20.4%与31.3%，残余位移分别减小42.7%与63.8%。同样，随着钢板厚度的增加，撞击区域混凝土的最大塑性应变值也有效地减小。在冲击荷载作用下，钢板厚度分别为14、18 mm的墙体，其最大位移时刻对应的背部钢板的Mises等效应力云图分别见图18～19。背部钢板中心区域的红色云图表示其应力已达到屈服值，通过对比可见，14 mm厚钢板的中间撞击部位区域均已屈服，而18 mm厚钢板的中间撞击部位区域，只有小部分区域达到屈服，大部分区域的应力小于或接近屈服应力。综上可得，对于厚度为0.80 m的钢板混凝土结构墙体，增大钢板的厚度能够有效地减小结构的最大位移、残余位移、混凝土的塑性应变以及钢板的等效应力等。

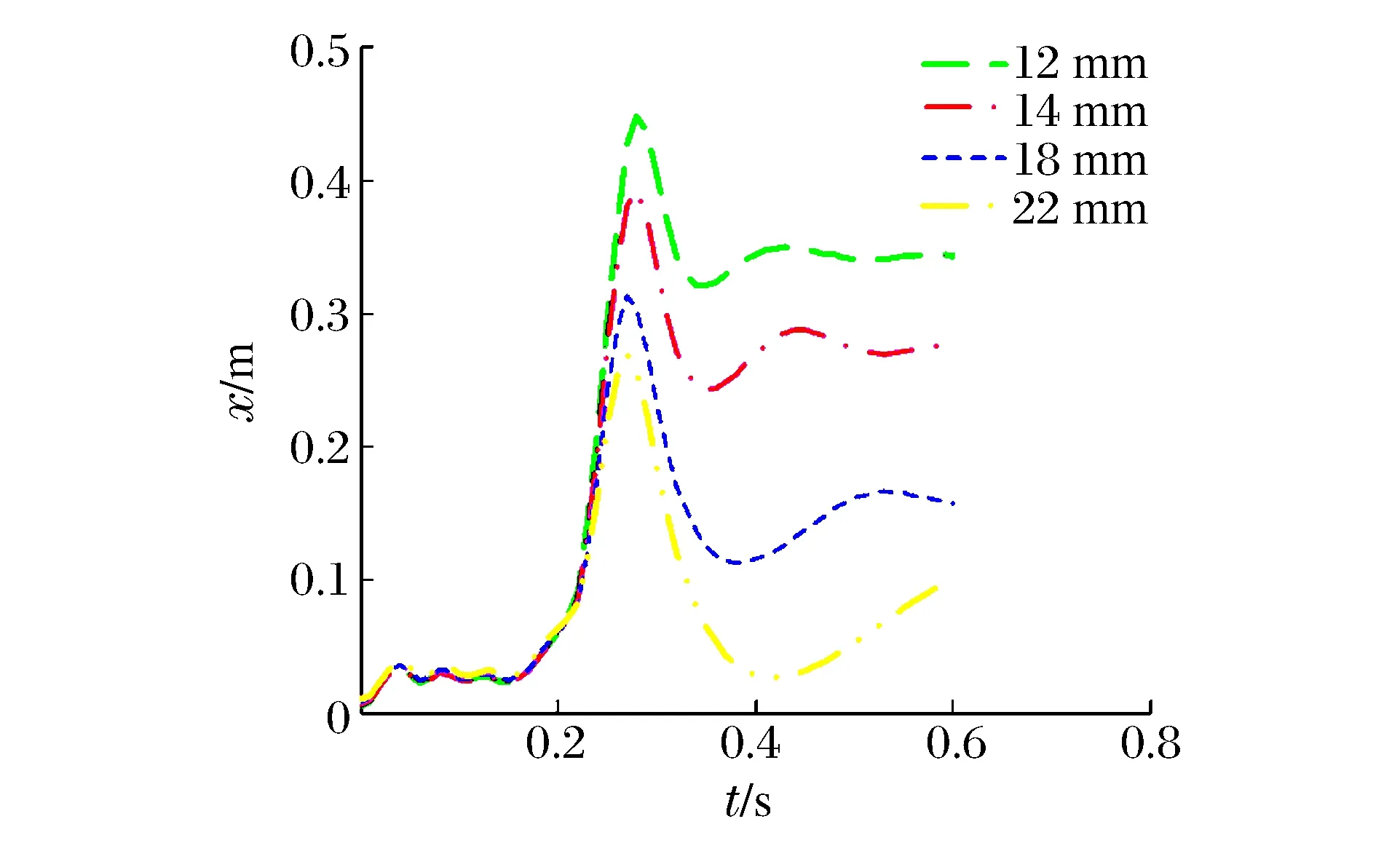
图16 不同钢板厚度的墙体最大位移时程曲线Fig.16 Curves of max displacement vs. time-historyfor SC wall of steel plates with different thickness

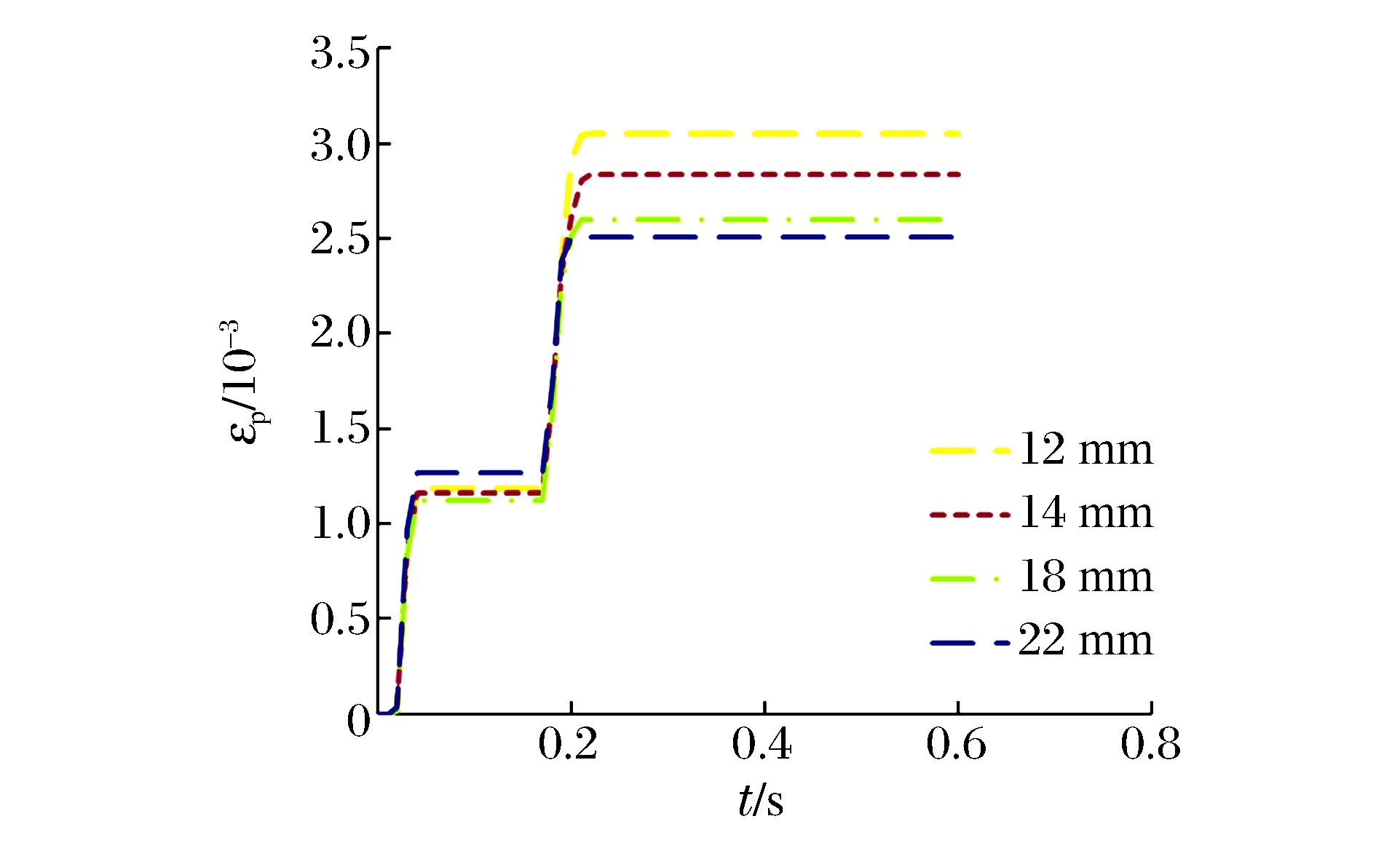
图17 不同钢板厚度的混凝土最大塑性应变时程曲线Fig.17 Curves of max plastic strain vs. time-historyfor concrete of steel plates with different thickness

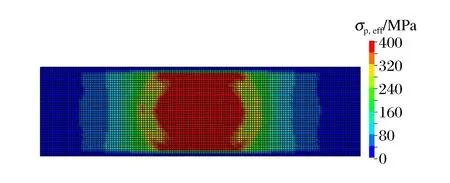
图18 SC墙体14 mm厚背部钢板的等效应力云图Fig.18 Contour plot of the equivalent stress of back faceof 14mm steel plate for SC wall

图19 SC墙体18 mm厚背部钢板的等效应力云图Fig.19 Contour plot of the equivalent stress of back faceof 18mm steel plate for SC wall

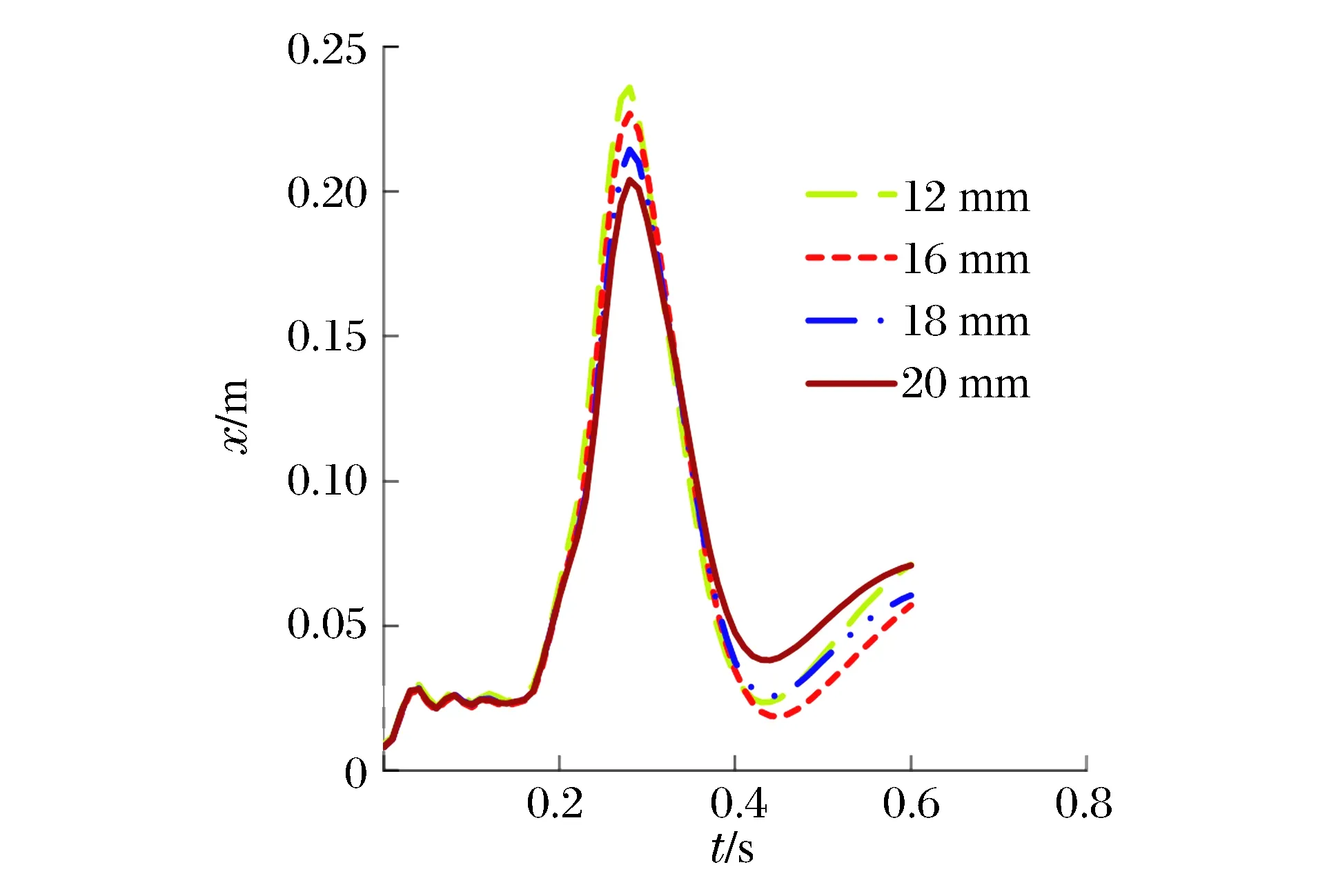
图20 不同拉结筋直径的墙体最大位移时程曲线Fig.20 Curves of max displacement vs. time-historyfor SC wall with different diameter of tie-bar

通过以上厚度为0.85、0.80 m的钢板混凝土结构墙体在不同厚度钢板情况下的冲击响应对比分析可知，总体来讲，增大钢板的厚度能够约束混凝土在撞击方向上的运动，有效地减小冲击作用下结构的响应，对于防护飞机撞击起到良好的作用。特别对于相对较薄的墙体，增加钢板的厚度在减小墙体的残余变形、混凝土的塑性应变以及钢板的有效应力等方面，其效果更显著。

3.4 不同拉结筋直径的敏感性分析

以墙体厚度为0.85 m、钢板厚度为16 mm、拉结筋间距为0.5 m的墙体作为研究对象，其拉结筋直径分别取为12、16、18和20 mm时，进行墙体结构响应的对比分析。通过如图20所示的撞击区域墙体背部沿冲击方向的最大位移时程曲线对比可得，拉结筋直径为12、16、18和20 mm的墙体，其最大位移值分别为23.6 、22.7、21.4和20.4 cm。可见，随着拉结筋直径的增大，墙体的最大响应略有减小，其效果不是很显著。可见增大拉结筋直径可有效地抵抗平面外剪力，但在顺着钢筋长度方向施加冲击荷载，抵抗飞机撞击的效果不明显。

3.5 不同拉结筋间距的敏感性分析

以墙体厚度为0.85 m、钢板厚度为16 mm、拉结筋直径12 mm的墙体作为研究对象，其拉结筋间距分别取为0.4、0.5、0.6 m，进行墙体结构响应的对比分析。当拉结筋的间距取为0.6 m时，墙体混凝土部分的最大位移云图见图21、其墙体背部的残余位移云图见图22、墙体前部和背部钢板的最大塑性应变云图见图23。从图21可见，墙体中心撞击区域的混凝土发生较大位移且部分被压碎，最大位移达到2.137 m，且此区域的剪力钉和拉结筋发生部分脱落。从图22可见，墙体背部中心区域的钢板被撕裂，最后混凝土与钢板的残余变形达到1.824 m；由于具有良好延展性的钢板的存在，约束了混凝土在撞击方向上的运动，虽然位移响应较大，仍限制了混凝土碎片的飞溅。从图23可知，前部和背部钢板均发生了局部破坏，最大塑性应变达到9.95%。当拉结筋间距取为0.5、0.4 m时，墙体背部节点的最大位移时程对比见图24，其最大位移分别为23.6、17.9 cm。墙体的前部和背部钢板仅局部发生塑性变形，没有单元发生失效。

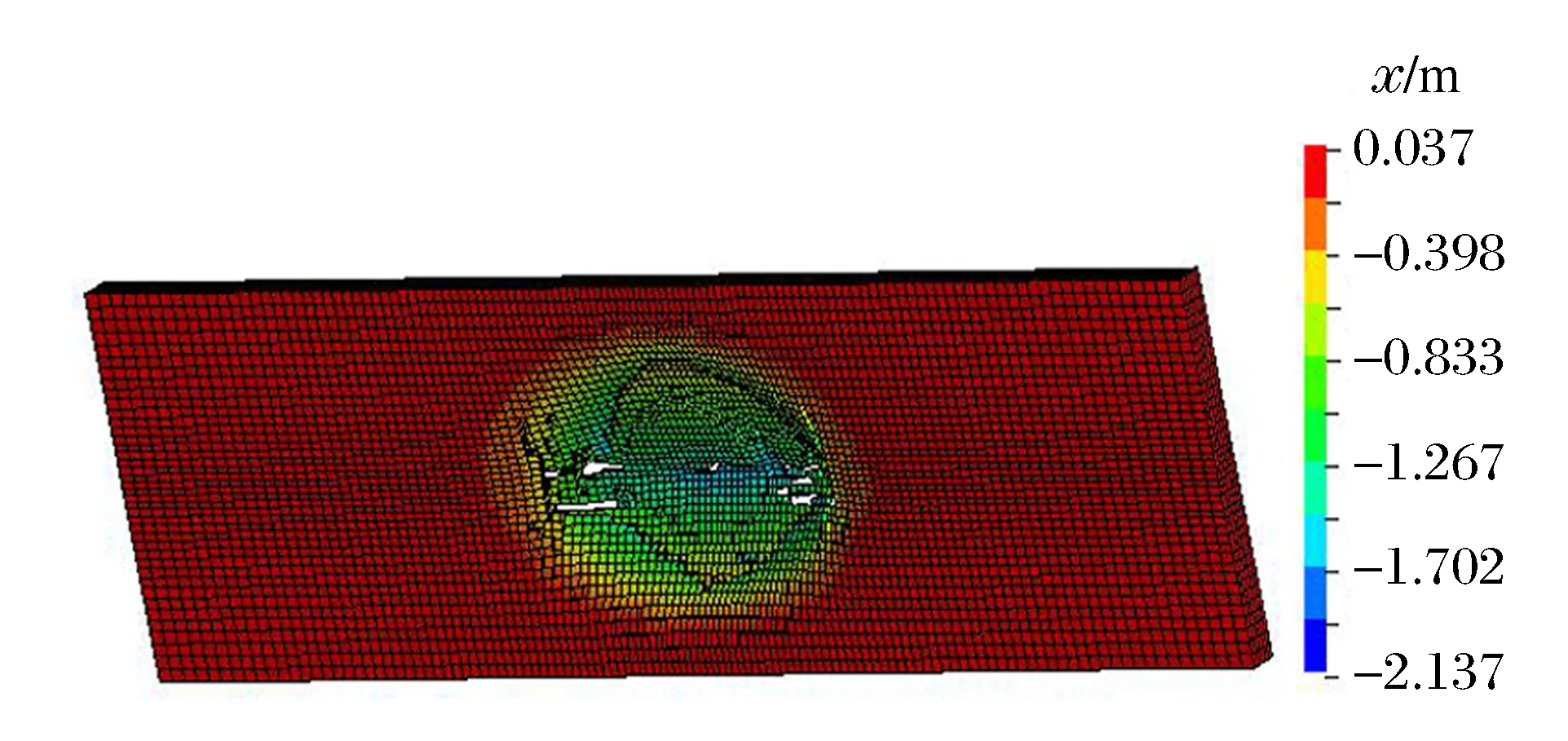
图21 混凝土的最大位移云图Fig.21 Contour plot of max displacement of concrete

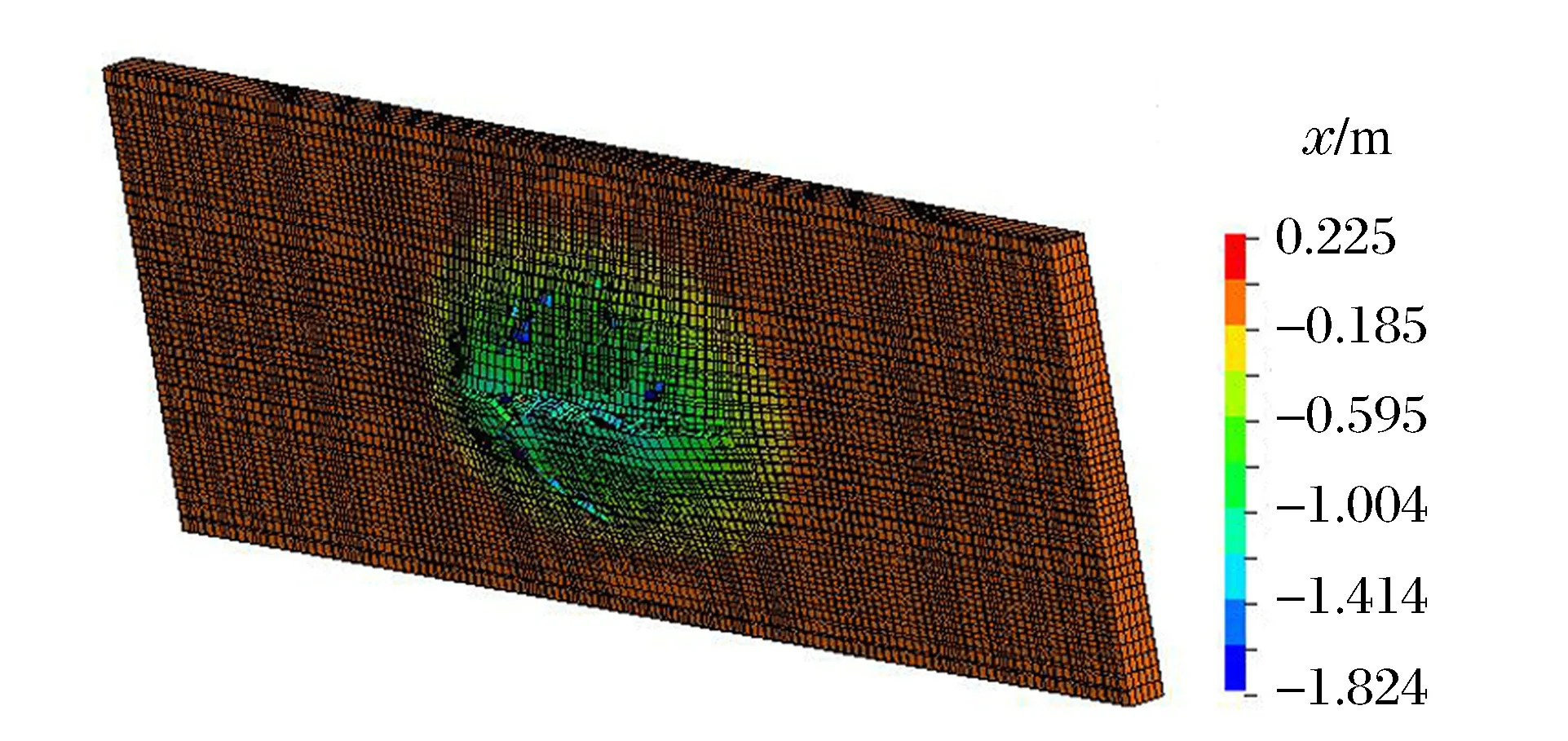
图22 SC墙体背部的残余位移云图Fig.22 Contour plot of residual displacement of SC wall back surface

图23 SC墙体钢板的最大塑性应变云图Fig.23 Contour plot of max plastic strain of SC wall steel plate

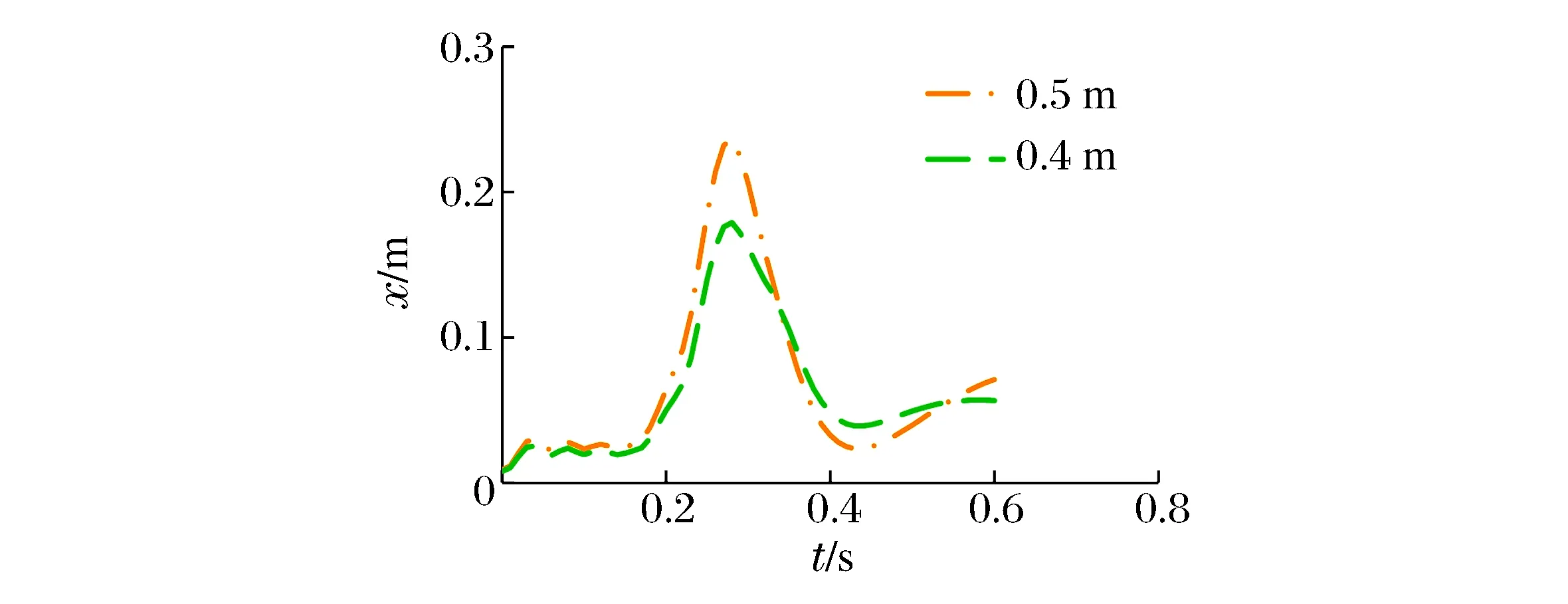
图24 不同拉结筋间距的墙体最大位移时程曲线Fig.24 Curves of max displacement vs. time-history for differently spaced tie-bar

通过对比以上不同拉结筋间距的墙体响应可知，拉结筋间距对墙体的抗冲击性能影响显著。若拉结筋间距过大，墙体的抗冲击性能较差，会发生整体破坏。拉结筋的加密有效地增强了钢板与混凝土之间的连接，提高了墙体构件的整体刚度，能够有效地提高墙体的抗冲击性能，以减小冲击作用下的结构响应，对于防护飞机撞击起到良好效果。

4 结 论

建立了三维钢板混凝土结构墙体的精细化有限元模型，基于荷载时程分析方法对影响钢板混凝土结构墙抗冲击性能的一系列参数进行了敏感性分析。这些参数包括混凝土厚度、钢板厚度和拉结筋直径与间距。得出结论如下：

(1)总体来讲，以上参数均会影响钢板混凝土结构墙体的抗冲击性能。增大混凝土与钢板厚度、增大拉结筋直径以及减小拉结筋与剪力钉间距，均有利于墙体抗冲击性能的提高。

(2)在其他参数不变的情况下，单方面的增大墙体混凝土厚度，即增大墙体的截面尺寸，对于提高钢板混凝土结构墙体的抗冲击性能效果显著，起到决定性作用。

(3)通过不同钢板厚度的结构响应敏感性分析，可以得出，增大钢板厚度能够有效地减小冲击作用下结构的响应，对于防护飞机撞击起到良好的作用。特别对于相对较薄墙体，增加钢板厚度能够有效的减小墙体的残余变形、混凝土的塑性应变以及钢板的有效应力等，其效果更显著。

(4)适当减小拉结筋间距，相对于增大拉结筋的直径，在减小结构的冲击响应、提高墙体的抗冲击性能方面，其效果更显著。

[1] US Nuclear Regulatory Commission.10CFR50.150 Aircraft impact assessment[S]. Washington, DC: US Nuclear Regulatory Commission, 2009.

[2] ERIN Engineering and Research, Inc. NEI 07-13, Revision 8P, methodology for performing aircraft impact assessments for new plant designs[S]. Palo Alto, 2011.

[3] Tsubota H, Koshika N, Mizuno J, et al. Scale model tests of multiple barriers against aircraft impact: Part 1. Experimental program and test results[C]∥Transactions of the 15th International Conference on Structural Mechanics in Reactor Technology (SMiRT-15). Seoul, Korea, 1999: VII137-VII144.

[4] Mizuno J, Koshika N, Sawamoto Y, et al. Investigations on impact resistance of steel plate reinforced concrete barriers against aircraft impact part 1: Test program and results[C]∥Transactions of the 18th International Conference on Structural Mechanics in Reactor Technology, 2005:2566-2579.

[5] Muhammad S, Zhu X Y, Pan R. Simulation analysis of impact tests of steel plate reinforced concrete and reinforced concrete slabs against aircraft impact and its validation with experimental results[J]. Nuclear Engineering and Design, 2014,273:653-667.

[6] 朱秀云,潘蓉,林皋,等.基于荷载时程分析法的钢筋混凝土和钢板混凝土墙的冲击响应对比分析[J].振动与冲击,2014,33(22):172-177. Zhu Xiuyun, Pan Rong, Lin Gao, et al. Comparative analysis of impact response with reinforced concrete and steel plate concrete walls based on force time-history analysis method[J]. Journal of Vibration and Shock, 2014,33(22):172-177.

[7] 潘蓉,吴婧姝,张心斌.钢板混凝土结构在核电工程中应用的发展状况[J].工业建筑.2014,44(12):1-7. Pan Rong, Wu Jingshu, Zhang Xinbin. Application and development of steel plate reinforced concrete structure in nuclear power engineering[J]. Industrial Construction, 2014,44(12):1-7.

[8] Hallquist J Q. LS-DYNA keyword user’s manual, revision 971[M]. California: Livermore Software Technology Corportion, 2007.

[9] 中国国家核安全局.HAD101/04.核电厂厂址选择的外部人为事件[S].北京：中国法制出版社,1989.

[10] Mullapudi T R S, Summers P, Hwan M. Impact analysis of steel plated concrete wall[C]∥Structures Congress 2012.ASCE, 2012:1881-1893.

[11] Arros J, Doumbalski N. Analysis of aircraft impact to concrete structures[J]. Nuclear Engineering and Design, 2007,237(12/13):1241-1249.

[12] Abu-Odeh A. Modeling and simulation of bogie impacts on concrete bridge rails using LS-DYNA[C]∥10th International LS-DYNA Users Conference. 2008.

[13] Comite Euro-International du Beton. CEB-FIP model code 1990[M]. Trowbridge, Wiltshire, U K: Redwood Books, 1993.

[14] Wu Y C, Crawford J E, Magallanes J M. Performance of LS-DYNA concrete constitutive models[C]∥12th International LS-DYNA Users Conference, 2012.

[15] 朱秀云,潘蓉,林皋,等.基于ANSYS/LS-DYNA的钢板混凝土墙冲击实验的有限元分析[J].爆炸与冲击,2015,35(2):222-228. Zhu Xiuyun, Pan Rong, Lin Gao, et al. FEM analysis of impact experiments with steel plate concrete walls based on ANSYS/LS-DYNA[J]. Explosion and Shock Waves, 2015,35(2):222-228.

[16] Mizuno J, Koshika N, Morikawa H, et al. Investigations on impact resistance of steel plate reinforced concrete barriers against aircraft impact. Part 2: Simulation analyses of scale model impact tests[C]∥Transactions of the 18th International Conference on Structural Mechanics in Reactor Technology, 2005:2580-2590.

(责任编辑 曾月蓉)

Sensitivity analysis for impact resistance of steel plate concrete walls based on force vs. time-history analysis

Zhu Xiuyun1,2, Lin Gao1, Pan Rong2, Lu Yu2

(1.LaboratoryofEarthquake,StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,Liaoning,China;2.PlantSiteandCivilEngineeringDepartment,NuclearandRadiationSafetyCenter,MinistryofEnvironmentalProtectionofPRC,Beijing100082,China)

In this paper, to study preventive ways against incidents involving the impact of steel plate concrete (SC) structures, the steel plate concrete (SC) walls composed of surface steel plates, tie-bars, shear studs and concretes were selected as the object of investigation. The impact analysis of the walls was performed using ANSYS/LS-DYNA, the FEM code, based on the force vs. time-history analysis, in which a series of numerical sensitivity studies were conducted to evaluate the effect of several parameters affecting the behavior of the SC wall. These parameters include the thickness of the wall, the thickness of the steel plate, and the diameter and space of tie bars. The results show that they all have an effect on the impact resistance of the SC wall. This is especially true with the thickness of the wall and the steel plate, and the spacing distance between the tie bars. These studies will serve as guidance and reference for the design of SC structures that are to be used in nuclear power plant buildings.

solid mechanics; behavior of impact resistance; force vs. time-history analysis; steel plate concrete wall; sensitivity analysis

10.11883/1001-1455(2016)05-0670-10

2015-02-04； < class="emphasis_bold">修回日期：2015-04-21

2015-04-21

国家科技重大专项基金项目(2011ZX06002-10)

朱秀云(1985— )，女，博士研究生,高级工程师,lyzhuxiuyun@163.com。

O347.1;TL371 <国标学科代码：13015 class="emphasis_bold"> 国标学科代码：13015 文献标志码：A国标学科代码：13015

A