SHPB帽形试样尺寸效应研究
2016-04-17肖大武何立峰
肖大武,马 策,何立峰
(中国工程物理研究院材料研究所,四川 江油 621908)
SHPB帽形试样尺寸效应研究
肖大武,马 策,何立峰
(中国工程物理研究院材料研究所,四川 江油 621908)
利用ANSYS/LS-DYNA软件开展不同尺寸帽形试样的SHPB数值模拟,研究帽形试样的尺寸效应。结果表明,当帽形试样剪切变形区域宽度大于0.2 mm时,根据经典公式处理得到的应力值将随t的增大而显著增大,严重偏离理论值,当t=1.0 mm时,计算得到的应力值甚至接近理论值的2倍。采用分体模型进行的进一步计算表明,数据处理结果中应力偏差主要来源于帽形试样中环状部位的膨胀变形。提出改进的数据处理方法,并采用圆柱样与几种不同尺寸帽形试样开展了验证实验,结果与计算结果基本一致。
固体力学;尺寸效应;ANSYS/LS-DYNA软件;帽形试样;SHPB
Hopkinson杆装置是材料绝热剪切行为研究中最常用的加载手段之一[1]。基于Hopkinson杆对绝热剪切实验的研究思路主要有以下几个方面:(1)利用传统的Hopkinson扭杆或压杆,研究在压缩或剪切状态下材料的绝热剪切行为;(2) 通过设计异形试样,包括帽形试样、斜圆柱样、阶梯圆柱样、圆台样、哑铃样、缺口圆柱样等,或改变加载方式,如双剪、冲压、切削实验装置,从而减小试样有效变形区长度来实现样品局域的高应变率剪切加载[2]。异形试样的使用可以将试样局域的应变率提高至104s-1以上,有利于绝热剪切的出现,但试样受力状态的复杂性也给数据结果的定量分析处理带来了难度。而以上列举的异形试样中除了帽形试样[3]和近年来提出的压剪试样[4],其他几种样品实验方法的基本原理分析不足,未提出成熟的实验方案和定量的数据处理方法。因此,应用最广的就是帽形试样SHPB实验方法,不仅可获得材料的绝热剪切变形特性,还可用于获得高应变率下材料的应力应变曲线。
在采用帽形试样进行材料绝热剪切特性的研究中,帽形试样尺寸各不相同[5-6]。U.Andrade等[3]提出帽形试样数据处理方法时,是假定变形区域为纯剪切应力状态,未对帽形试样的尺寸效应进行详细分析,若在试样剪切区域受力状态较复杂时,仍采用该公式处理数据,可能产生错误[7]。本文中拟通过数值模拟,考察帽形试样的尺寸效应对数据处理的影响,并开展一系列不同尺寸帽形试样的SHPB数值实验来着重研究剪切变形区域宽度对帽形试样局域应力状态及数据处理结果带来的影响,给出了能获得有效应力应变曲线的帽形试样尺寸要求及改进的数据处理方法,并验证方法的有效性。

图1 帽形试样示意图Fig.1 Schematic of hat-shaped specimen
1 数值模拟
1.1 模拟方法
采用ANSYS/LS-DYNA软件开展不同尺寸帽形试样的SHPB数值实验,帽形试样简图如图1所示。模拟中入射杆和透射杆尺寸取为∅14.5 mm×1 000 mm,帽形试样尺寸如表1所示, 在其他部位尺寸不变的同时,通过改变帽形试样底部内径r2来调节剪切区域的宽度t,从而比较分析其对帽形试样变形过程中的剪切区域应力、应变状态和数据处理结果的影响。

表1 帽形试样几何尺寸Table 1 Physical dimensions of the hat-shaped specimens

图2 帽形试样网格划分图Fig.2 Grid partition of hat-shaped specimen
采用二维轴对称模型建模,选取的单元类型为plane 162单元。杆的网格尺寸长度方向为3 mm,直径方向为1 mm,帽形试样网格尺寸为0.5 mm,剪切变形区及附近区域网格细化为约50 μm,如图2所示。压杆材料为60Si2MnA,采用线弹性模型,密度为7 740 g/cm3,弹性模量为206 GPa,泊松比为0.29;试样采用Johnson-Cook本构模型,密度为7 800 g/cm3,弹性模量为200 GPa,泊松比为0.30,屈服强度A=496 MPa,硬化强度B=434 MPa,应变硬化指数n=0.304,应变率敏感系数C=0.07,热软化系数m=0.804,熔点温度Tm=1 765 K,质量定压热容cp=452 J/(kg·K) 。
1.2 结果分析
计算中通过在入射杆端面施加梯形速度脉冲进行加载,速度脉冲幅值为20 m/s,脉冲持续时间为100 μs,上升沿和下降沿均为10 μs。采用U.Andrade等[3]提出的公式对计算结果数据进行处理,得到不同尺寸帽形试样的应力应变曲线与J-C模型(应变率取2×105s-1计算),如图3所示。由图中可以看出,随着剪切区域宽度t的增大,相应的应力应变曲线与J-C模型之间的偏差显著增大,当t=0.2 mm时,应力与模型计算值基本一致。而当t增大至1.0 mm时,应力接近模型计算值的2倍。计算得到的应力值高于模型的,这是由于参与剪切区域变形的载荷被高估造成的。为了分析应力偏差的来源,采用分体模型来考察帽形试样中剪切变形区域外基体发生变形对透射信号的影响。材料模型参数不变,将帽形试样分解为楔块和环状样2个部分,接触面设定为无摩擦接触,如图4所示。

图3 不同尺寸帽形试样计算结果[3]与J-C模型对比图Fig.3 Comparison of calculation between simulation[3] and J-C model

图4 分体模型示意图Fig.4 Schematic of the split model
图5中分别给出了之前3种不同尺寸帽形试样整体模型与分体模型的透射载荷与轴向位移的关系图,实心点为整体模型计算结果,空心点为分体模型计算结果。由图可知,随着剪切区域宽度t增大,环状样部分膨胀变形引起的载荷占整体透射载荷的比例显著提高。当t=0.5 mm时,帽形试样中膨胀载荷占透射载荷的比例约为30%,当t=1.0 mm时,帽形试样中膨胀载荷占透射载荷的比例迅速提高至约70%。而只有当t=0.2 mm时,试样中的膨胀载荷较小,近似满足理论分析时基体弹性变形假设。由此可见,应力偏差主要来源于环状样的膨胀变形。随着t的增大,帽形试样变形过程中有相当可观的载荷会消耗在环状样的变形过程中,使得测量到的透射载荷不断增强,从而整体抬高了透射信号的幅值,处理出来的应力应变曲线也相应偏高。

图5 分体模型膨胀载荷分析Fig.5 Calculation of the expansion load in split model
由前文的分析可知,随着帽形试样中宽度t的增大,剪切变形区的应力状态已不能考虑为单一的剪切变形状态,而是复杂应力、复杂应变状态,这时若仍采用U.Andrade等[3]提出的公式计算应力应变曲线将可能导致严重失真。图6给出了t=0.5 mm的帽形试样的应变云图,由图中可以看到沿剪切变形区域的应变并不均匀。对t>0.2 mm时帽形试样的计算结果进行了进一步的分析处理,试图对相应帽形试样变形区域内的应力、应变状态进行近似的估算。参照D.Rittel等[4]对压剪试样的应力应变曲线数值验证的思路,考虑只有部分轴向加载引起剪切区变形,同时扣去变形过程中的径向载荷,采用的应力、应变表达式如下:
(1)
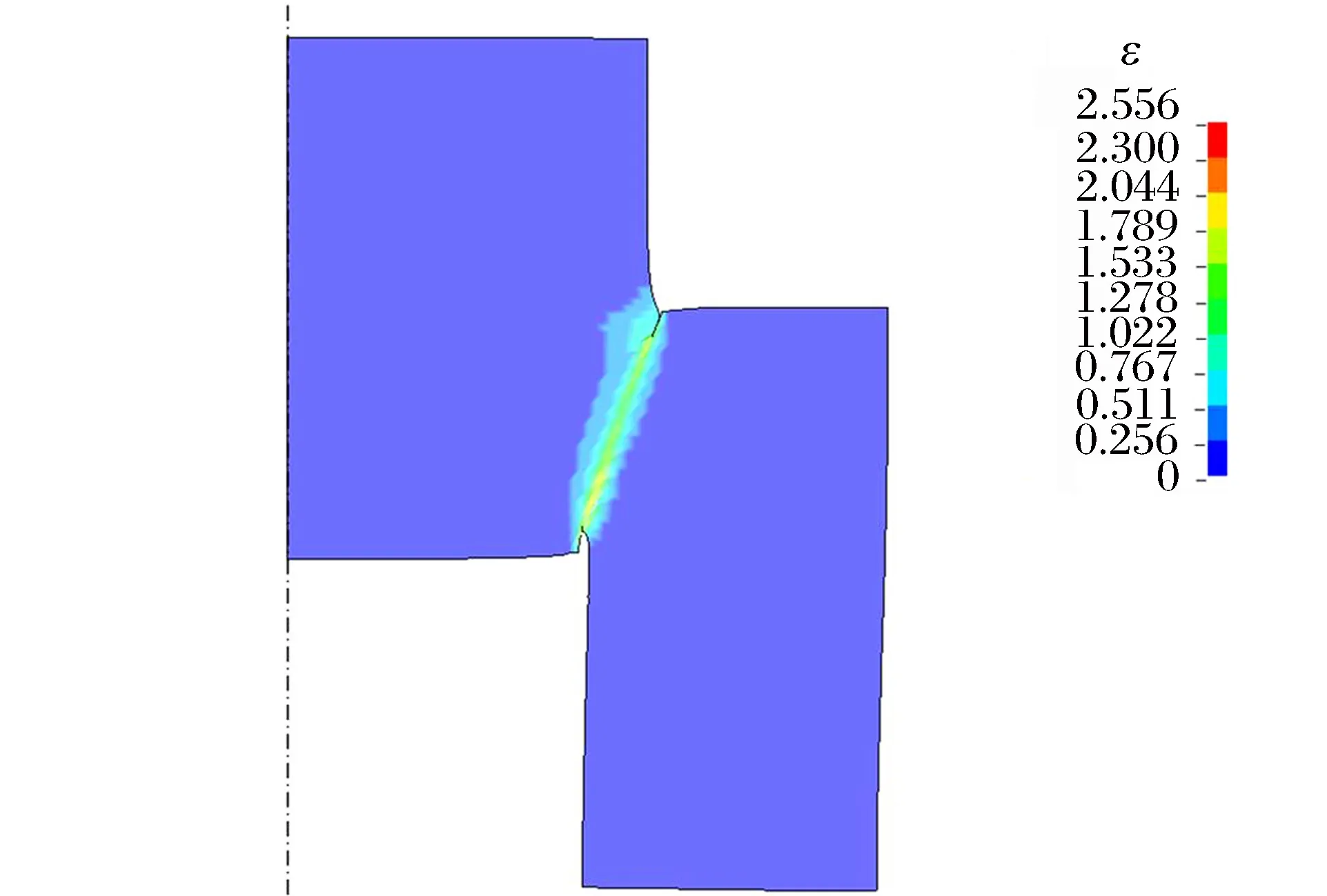
图6 帽形试样应变分布云图Fig.6 Contour graph of strain in hat-shaped specimen


表2 应力、应变表达式形状相关参数Table 2 The geometry-related parameters in stress and strain expressions
2 实验验证
为了考核前面的计算结果,进行圆柱样品与不同尺寸帽形试样的SHPB验证实验,实验结果如图7所示。图7(a)为按照参考文献[3]中公式处理出来的帽形样实验结果与圆柱样结果比对。由图可知,不同t值的帽形试样处理得到的应力应变曲线有较大差异,只有t=0.2 mm时结果与圆柱样结果基本一致,而t值较大的帽形试样处理出来的应力幅值明显高过圆柱试样的处理结果,且t值越大差异也越大,当t=1.0 mm时应力幅值甚至达到圆柱样的3倍,这与前文数值模拟结果反应出来的规律一致。图7(b)所示为采用式(1)处理得到的结果,可以看到此时不同t值帽形试样的应力曲线与圆柱试样的曲线基本一致,这也表明可用该方法对t值较大时的帽形试样中的应力应变状态进行大致估算。对于不同几何尺寸和材料类型的帽形试样,式(1)中参数可采用圆柱样的实验结果结合数值模拟进行估算。当然,若变形区内应力、应变的分布极不均匀时,采用式(1)也无法得到较好的估算结果。

图7 不同公式处理的得到的应力应变曲线对比Fig.7 Comparison of stress-strain curves calculated by different formula
3 结 论
开展了不同尺寸帽形试样的SHPB数值试验,研究了尺寸效应对帽形试样变形状态及数据处理结果的影响,随剪切变形区域宽度的增大,采用传统公式处理得到的应力应变曲线偏差越大。通过进一步的数值模拟分析,发现偏差主要来源于变形过程中帽形试样环状部分的膨胀变形。基于数值模拟结果,针对剪切变形区域宽度较大的帽形试样提出了一套新的数据处理方法,并开展了相关的验证实验。实验结果与数值模拟得到的规律基本一致,新的处理方法可用于近似估算此时帽形试样的变形状态。
[1] Zukas J A , Nicholas T , Swift H F , et al. Impact dynamics[M]. Malabar, Florida: Krieger Publishing Company, 1992.
[2] 肖大武,李英雷,蔡灵仓.绝热剪切研究进展[J].实验力学,2010,25(4):463-475. Xiao Dawu, Li Yinglei, Cai Lingcang. Progress in research on adiabatic shearing[J]. Journal of Experimental Mechanics, 2010,25(4):463-475.
[3] Andrade U, Meyers M A, Vecchio K S, et al. Dynamic recrystallization in high-strain, high-strain-rate plastic deformation of copper[J]. Acta Metallurgica et Materialia, 1994,42(9):3183-3195.
[4] Rittel D, Dorogoy A. Numerical validation of the shear compression specimen. Part I: Quasi-static large strain testing[J]. Experimental Mechanics, 2005,45(2):167-177.
[5] 刘新芹,谭成文,张静,等.应力状态对Ti-6Al-4V绝热剪切敏感性的影响[J].稀有金属材料与工程,2008,37(9):1522-1525. Liu Xinqin, Tan Chengwen, Zhang Jing, et al. Influence of stress-state on adiabatic shear sensitivity of Ti-6Al-4V[J]. Rare Metal Materials and Engineering, 2008,37(9):1522-1525.
[6] 陈思颖,黄晨光,孔卫国,等.结构钢中绝热剪切带形成与扩展的光学观测与数值模拟响[J].高压物理学报,2010,24(1):31-36. Chen Siying, Huang Chenguang, Kong Weiguo, et al. Optical observation and numerical simulation on the evolution of adiabatic shear band in structural steel[J]. Chinese Journal of High Pressure Physics, 2010,24(1):31-36.
[7] Wang B F, Yang Y. Microstructure evolution in adiabatic shear band in fine-grain-sized Ti-3Al-5Mo-4.5V alloy[J]. Materials Science and Engineering: A, 2008,473(1/2):306-311.
(责任编辑 王易难)
本刊关于稿件、版权等的声明
在投稿、稿件处理、发表等过程中,作者需注意如下问题:
1.稿件是作者独立取得的原创性研究成果,无抄袭,无一稿多投,未在国内外公开发表过。
2.稿件无政治错误,不涉及保密和拟申请专利的内容,已经过作者单位保密审查。
3.作者署名和排序无异议,单位署名和排序无争议,且无知识产权纠纷。在稿件处理过程中,如有作者或单位署名变更,需有全体作者亲笔签名和全部单位盖章同意的书面声明。
4.稿件由编辑部组织审稿。自收稿之日时,编辑部将在4个月内反馈处理结果。若超过4个月未答复的,作者有权另行处理稿件,但需事先通知编辑部。
5.对录用的稿件,在尊重稿件内容的基础上,编辑部有权作必要的修改和删减,按规定进行标准化和规范化。
6.稿件录用后,稿件的所有出版权归编辑部。
7.稿件发表后,编辑部赠送样刊,并一次性付给作者稿酬及版权转让费。
爆炸与冲击
2016年1月25日
Dimensional effects of hat-shaped specimen in Hopkinson bar test
Xiao Dawu, Ma Ce, He Lifeng
(InstituteofMaterials,ChinaAcademyofEngineeringPhysics,Jiangyou621908,Sichuan,China)
Numerical Hopkinson bar experiments of hat-shaped specimens with different geometries were carried out using ANSYS/LS-DYNA to investigate the effects resulting from varying the geometrical dimensions of specimens. Results show that the stress value calculated by the classic formula deviated drastically from the theoretical value, when the widthtthe of shear zone was larger than 0.2 mm. When the widthtwas 1.0 mm, the calculated stress value would even rise up to twice as much as close to the theoretical value. Further research with the split model revealed that the deviation of the stress mainly occurred as a result from the expansion deformation of the brim portion of the hat-shaped specimen. An improved method of data processing for the hat-shaped specimen was also presented based on the numerical simulation results. Finally, the method was also validated by SHPB experiments with cylinder specimens and hat-shaped specimens with different dimensions.
solid mechanics; geometry effect; ANSYS/LS-DYNA; hat-shaped specimen; SHPB
10.11883/1001-1455(2016)01-0064-05
2013-11-11; < class="emphasis_bold">修回日期:2014-01-25
2014-01-25
肖大武(1983— ),男,博士,副研究员,hopkinson@163.com。
O347 <国标学科代码:13035 class="emphasis_bold"> 国标学科代码:13035 文献标志码:A国标学科代码:13035
A
