轿车车内中频噪声的FE-SEA混合分析*

贺岩松，张 辉，夏小均，徐中明，张志飞

(1.重庆大学，机械传动国家重点实验室,重庆 400030； 2.重庆大学汽车工程学院,重庆 400030)

2016120

轿车车内中频噪声的FE-SEA混合分析*

贺岩松1,2，张 辉2，夏小均2，徐中明1,2，张志飞1,2

(1.重庆大学，机械传动国家重点实验室,重庆 400030； 2.重庆大学汽车工程学院,重庆 400030)

建立了某一轿车的混合FE-SEA模型和SEA模型，计算了各子系统的模态密度、内损耗因子和耦合损耗因子。通过试验测量了匀速50km/h时的发动机舱的声辐射激励、动力总成悬置点的激励和路面不平度对车身悬置点的激励。采用混合FE-SEA模型和SEA模型分别预测了驾驶员右耳旁声压级，并与试验结果进行对比，表明了200～1 000Hz整个中频范围内混合FE-SEA模型的预测精度比SEA模型高。把能量注入法计算的内损耗因子重新加载到混合FE-SEA模型上进行计算，结果表明，在中频段预测精度得到了提高。最后对混合FE-SEA模型分别施加各悬置点的振动激励和发动机舱声辐射激励进行计算，分析了不同频率段车内噪声的主要激励源。

中频噪声；混合FE-SEA模型；能量注入法；预测

前言

目前，车内低频噪声CAE预测分析可以通过有限元法(finite element method，FEM)和边界元法 (boundary element method，BEM)得到很好的解决，对于车内高频噪声的预测分析使用统计能量分析法(statistical energy analysis，SEA)可以得到比较高的求解精度，而处于200～1 000Hz的中频噪声预测分析目前仍然是一个难题[1-2]。为解决这一难题，国外一些学者将FEM和SEA结合起来，采用动力平衡方程和功率平衡方程计算声振系统的响应，形成了目前的混合FE-SEA方法[3-4]。

混合FE-SEA方法能有效提高传统FEM和SEA在中频域的预测精度，因此该方法在中频声振预测分析领域得到了广泛的应用。文献[5]中使用FE模型来求解SEA子系统的模态密度等参数,由于该方法可以考虑一些子系统的结构细节,从而有助于提高SEA模型的预测精度。该方法说明，使用FE模型求解模态密度可以提高SEA模型的预测精度，但是并未进一步研究使用FE模型来求解内损耗因子时对模型预测精度的影响。文献[6]和文献[7]中建立了全内饰混合FE-SEA模型，对车内200～1 000Hz的中频噪声进行了预测，使用噪声传递路径分析法来确定车内噪声的关键贡献子系统，对它们采用添加阻尼或声学包优化的方法来降低车内噪声。该方法在降低车内中频结构噪声方面取得了良好的效果，但该混合模型没有施加发动机声辐射激励，不能反映真实的车内中频噪声传递路径。文献[8]和文献[9]中建立了网格大小为40mm的混合FE-SEA模型，计算了各子系统的辐射效率，研究了使用FEM计算模态密度时对模型预测精度的影响，比较了20～1 000Hz范围内FE-SEA模型与SEA模型的预测精度。这两篇文献中在车内中频噪声分析领域做了比较深入的研究，但未对不同频率段车内中频噪声的形成机理进行进一步的研究。

本文中总结了混合FE-SEA建模的基本原则，通过试验测量了匀速50km/h工况下发动机舱声辐射激励、动力总成悬置点的激励和路面不平度对车身悬置点的激励。在200～1 000Hz频率范围内分析了使用不同方法计算内损耗因子时对混合FE-SEA模型预测精度的影响；通过在混合模型上施加不同种类的激励，分析了不同频率段车内噪声的主要激励源，对车内中频噪声降噪分析有一定的指导意义。

1 轿车混合FE-SEA模型的建立

在VA One中建立混合FE-SEA模型分两大步:第一步在hypermesh中对几何模型或有限元模型进行适当的简化，然后进行节点耦合处理并调整网格质量；第二步在VA One中根据有限元模型的单元和节点信息分别建立FE子系统和SEA子系统，并生成有效的连接，建立完整的混合FE-SEA模型。

1.1 模型部件的简化

为了便于有效建模，首先要对有限元整车模型进行适当简化。模型简化的原则是：(1)处于车身边缘的小零件，对系统整体振动性能影响不大，建模时可删除；(2)对于大块的平面板件，在混合模型中必须使用SEA子系统来建模，由于SEA板的中部与有限元子系统无法生成混合连接，因此这种板件上面的细小附件要删除；(3)与车内声腔子系统相连的面必须严格封闭且不能重叠，为了方便建模，需要删除声腔包络面上一些对整体振动性能影响不大但很大程度上增加建模难度的部件；(4)VA One软件中不能识别高阶单元，因此用体单元建模的胶粘层必须删除。

1.2 模型的节点耦合处理

为了建立更加精确的混合FE-SEA模型，可按照下列方法进行节点耦合：(1)与车内声腔直接接触的包络面板件，最好在构件的边缘处共节点，或者在合适的位置共节点之后，将重叠或多余的部分单独生成一个部件或者直接删除;(2)对于梁、杆等结构，尽量按照原连接的位置或者相近的位置进行共节点连接;(3)节点耦合后需要在hypermesh中检查相应的自由边并调整网格质量。

1.3 声腔包络面的修补和构件的重划分

在VA One中，声腔包络面必须是严格密封且没有孔洞的，因此建模时要对有限元模型中一些板件上的孔洞进行填补。图1(a)和图1(b)是防火墙孔洞填补前后对比图。

为了方便在VA One中建立SEA声腔子系统，使SEA子系统和FE子系统之间能够生成有效的连接，需要对有限元模型中声腔包络面的构件进行重划分，划分后的子系统放在单独的component中。图1(c)和图1(d)为车身顶部构件划分前后对比图。

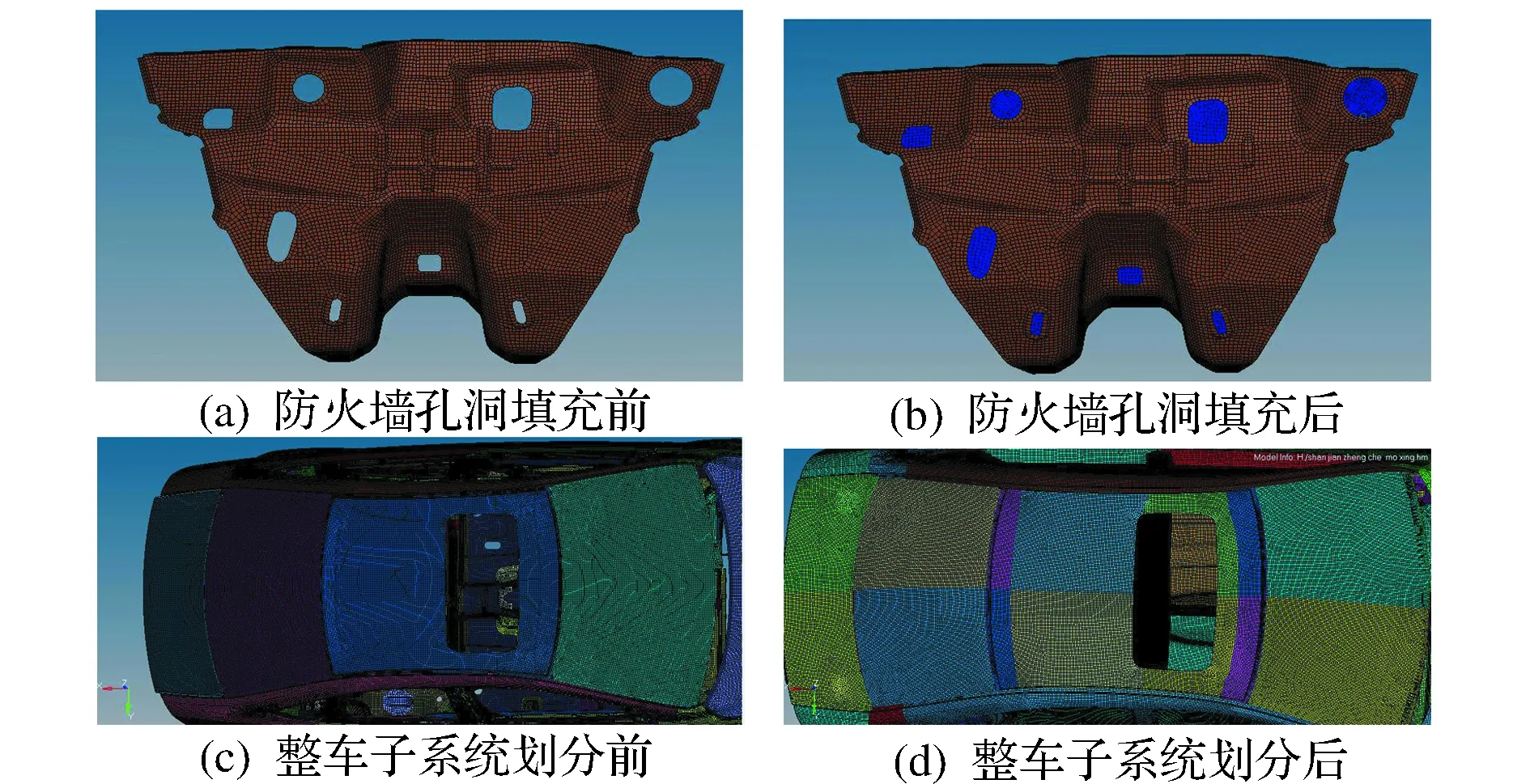
图1 孔洞的填补和构件重划分

1.4 混合FE-SEA模型和SEA模型的建立

在VA One中，将单位频带上模态数小于5的构件(如A柱、B柱和梁结构等)建成FE子系统，如图2(a)所示；将其余的构件建成SEA板子系统；根据建成的FE和SEA板子系统建立相应的声腔，建立的声腔子系统如图2(b)所示。最后对各子系统进行连接，使各个子系统之间耦合良好，保证能量能够在各个子系统中相互传递。

建立的混合FE-SEA模型如图2(c)所示，该混合模型含有130个FE子系统、97个SEA板件子系统和14个声腔子系统。完整的有限元模型中共有732 489个网格大小为8mm的单元，而混合FE-SEA模型中仅包含322 345个网格单元，与完整有限元模型相比网格单元减少了56%，从而大大减少了中频段模型的求解时间。

为了比较混合FE-SEA方法和SEA法在200～1 000Hz中频段的求解精度，本文中还建立了如图2(d)所示的SEA模型，SEA建模过程与混合FE-SEA建模基本相似。

图2 混合FE-SEA模型和SEA模型

2 轿车模型参数的计算

统计能量模型包括模态密度、内损耗因子和耦合损耗因子这3个参数，这些参数计算的准确性直接关系到模型的预测精度，因此在实际应用中须根据不同情况采用不同的方法对各个子系统的模型参数进行计算。

2.1 模态密度

模态密度是描述子系统贮存能量能力大小的一个物理量，表示子系统在单位频段内的模态数[10]。二维平板模态密度的理论计算公式为

(1)

式中：f为1/3倍频程中心频率；A为平板面积;E为平板弹性模量;ρ为平板体积密度;μ为平板泊松比;h为平板厚度。

声腔子系统的模态密度计算公式为

(2)

式中：V为声场的体积;A为声场的表面积;l为声场的棱边长度;c为声音在空气中的传播速度。

简单子系统的模态密度由理论公式计算获得，如图3所示，在200～1 000Hz中频范围内，平板子系统的模态密度为不随频率变化的常量，曲面板和声腔子系统的模态密度随频率的增大而增大。

图3 简单子系统模态密度理论计算值

对复杂子系统模态密度公式的推导非常困难，若对子系统进行简化再利用理论公式进行计算则误差较大[11]。工程上目前得到复杂子系统模态密度的方法主要有导纳实部平均法和FEM，这两种方法各自有自己的优势和局限。由于在中频段模态重叠现象不明显，且在混合FE-SEA建模前期需要初步估计各子系统在单位频带上的模态数，因此本文中对复杂子系统的模态密度采用FEM计算。由定义可知，FEM计算子系统模态密度的公式为

(3)

式中：N为频带上的模态数；fu和fl分别为1/3倍频程中心频率的上限和下限频率。

使用FEM计算得到200～1 000Hz的模态密度如图4所示。

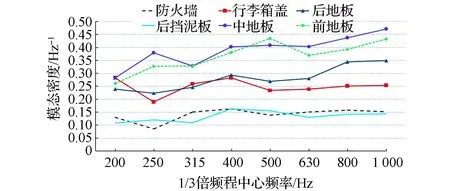
图4 复杂子系统模态密度FEM计算值

2.2 内损耗因子

2.2.1 理论公式计算内损耗因子

在统计能量分析法中，内损耗因子指子系统在单位频率内单位时间的损耗能量与子系统平均存储能量的比值。简单平板和曲面板子系统的内损耗因子可以根据理论公式进行Matlab编程计算获得，声腔内损耗因子可以通过60dB衰减法或者平均吸声系数法获得。当汽车处于研发阶段，无法在实车上进行60dB衰减试验时，则可使用平均吸声系数法来求得各声腔子系统的内损耗因子。根据加载在模型上的声学包装材料，求得各个声腔表面Sn的吸声系数an，则声腔的空间平均吸声系数为

(4)

由于计算频率范围为200～1 000Hz且车内声腔体积不大，因此得到的声腔空间平均吸声系数可以不用修正，根据平均吸声系数可由以下经验公式计算混响时间：

(5)

从而可以计算出声腔内损耗因子：

(6)

式中：S为声腔子系统表面积；V为声腔子系统体积。

根据理论公式计算各平板、曲面板和声腔子系统的内损耗因子如表1所示，在200～1 000Hz范围内各子系统的内损耗因子均随频率的增大而减小。

表1 子系统内损耗因子

2.2.2 能量注入法计算内损耗因子

在工程上获取内损耗因子的最常用和可靠的方法是通过试验测量。测量内损耗因子的方法主要有模态法(又称半功率点带宽法)和脉冲响应衰减[12]。在车辆设计、开发的早期阶段，很难获得各个子系统对应的实际构件，因此无法通过试验测量实际结构的内损耗因子，本文中根据能量注入法的基本原理计算各子系统的内损耗因子。由内损耗因子的定义可得：

(7)

式中：Pd为单位时间损耗的能量；w为1/3倍频程中心圆频率；E为子系统平均存储的能量。

当结构在连续稳定的宽带随机激励下达到稳态振动时，系统输入功率Pin与损耗功率Pd相等，因此式(7)可以改写为

(8)

式中：F为输入点激励力；Vo为输入点的速度响应；m为结构质量；为空间平均的振动速度均方值。

如图5所示，在FE子系统上选择合适位置施加激励力，在激励点上布置传感器测量激励点的振动速度，同时在子系统的其他位置尽可能多地均匀布置传感器，对各个测点的振动速度求均值得到子系统的平均振动速度，进而求得子系统空间平均的振动速度均方值。综合考虑计算精度和计算时间等因素，本文中对每个子系统选择8个点依次进行激励，子系统上总共布置30个传感器用来测量各测点的振动速度，最终的计算结果如图6所示，前车门、防火墙、顶棚和中地板等子系统的内损耗因子的总体趋势是随频率的增大而减小，但在某些频率段有一定的波动。

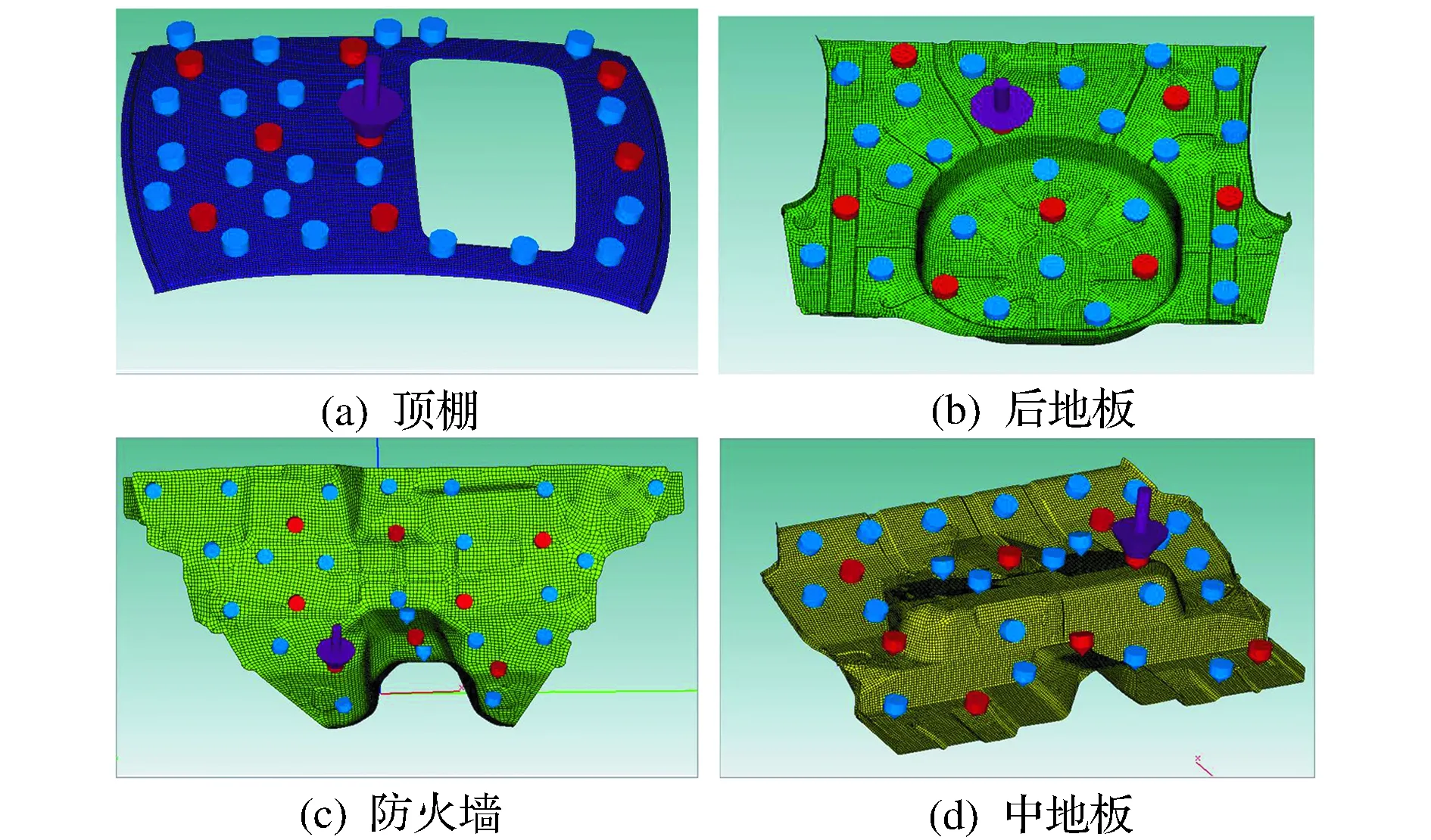
图5 激励点和传感器位置的布置

图6 能量注入法的内损耗因子计算值

2.3 耦合损耗因子

耦合损耗因子ηij是描述能量从子系统i传到子系统j损耗特性的一个物理量,是两个子系统之间耦合程度强弱的一种度量。根据耦合方式的不同,子系统之间的耦合可以分为点连接、线连接和面连接；根据子系统性质的不同，子系统之间的耦合可分为结构-结构耦合、结构-声腔耦合和声腔-声腔耦合。

设子声腔a与子结构s之间存在面连接，记ρa为声场a的体积质量密度，c为声速，ρs为结构的面积质量密度，σsa为结构的辐射比，那么结构s到声场a的耦合损耗因子ηsa为

(9)

驾驶员头部声腔与左前风窗玻璃的耦合损耗因子如图7所示。

图7 驾驶员头部声腔与左前风窗玻璃间的耦合损耗因子

3 轿车模型激励的测试

汽车行驶过程中所受外部激励主要有:发动机舱声辐射激励、动力总成悬置振动激励、路面不平度对车身悬置点的激励和车外风激励。由于本文中测量车速为50km/h，在低速下车外风激励的作用对车内噪声的影响不大[13]。本文中的试验车辆发动机为三点悬置，前悬架为麦弗逊式独立悬架，后悬架为双叉臂式独立悬架。试验仪器主要包含3个传声器、7个三向加速度传感器、一台speedbox、一台32通道B&K数据采集器和一台笔记本电脑，部分传感器安装位置如图8所示。

测试过程中车速以50km/h匀速行驶，采样时间为10s，试验重复进行3次。对测得的时域信号截取时间长度为5s的平稳段进行分析，将3次处理后的信号做平均处理，得到减振器与车身左前减振塔连接处X，Y和Z3个方向上的加速度激励，如图9所示。发动机舱防火墙处的声辐射激励如图10所示。

图8 传感器安装位置示意图

图9 车身左前悬减振塔处振动激励

图10 发动机舱防火墙处声辐射激励

4 车内中频噪声预测分析

4.1 模型验证

根据已有的声学材料参数在VA One中建立相应的声学包材料，进一步建立与整车相同的声学包，并加载在相应的子系统上，整车各子系统声学包如表2所示。

把50km/h车速下测得的激励加载到混合FE-SEA模型和SEA模型上，加载相同的声学包和模型参数，并对驾驶员右耳旁声压级进行仿真计算，结果如图11所示。在200～1 000Hz的中频范围内，与SEA模型相比，混合FE-SEA模型的预测值更加接近试验测量值，不仅验证了在中频范围内混合FE-SEA模型的预测精度更高，而且证明了本文中提出的混合建模方法是可靠的。

4.2 不同方法计算的内损耗因子对车内噪声预测精度的影响

将能量注入法计算的内损耗因子重新加载到混合FE-SEA模型上进行计算，并与加载理论公式计算内损耗因子的混合模型预测值进行对比，结果如表3所示。使用理论公式计算内损耗因子时，车内噪声预测值与试验测量值的最大误差为2.45dB, 误差绝对值的平均值为1.8dB；使用能量注入法计算内损耗因子时，最大误差减小到1.91dB，误差绝对值的平均值为1.44dB，说明采用能量注入法计算内损耗因子时能提高混合FE-SEA模型在中频范围内的预测精度。其主要原因可能是对于某些结构子系统，上面的孔洞和加强筋对内损耗因子影响较大，使用理论公式计算不能反映真实情况，因此计算结果误差较大；采用能量注入法计算内损耗因子时可以考虑结构的细节，计算更加符合真实情况。

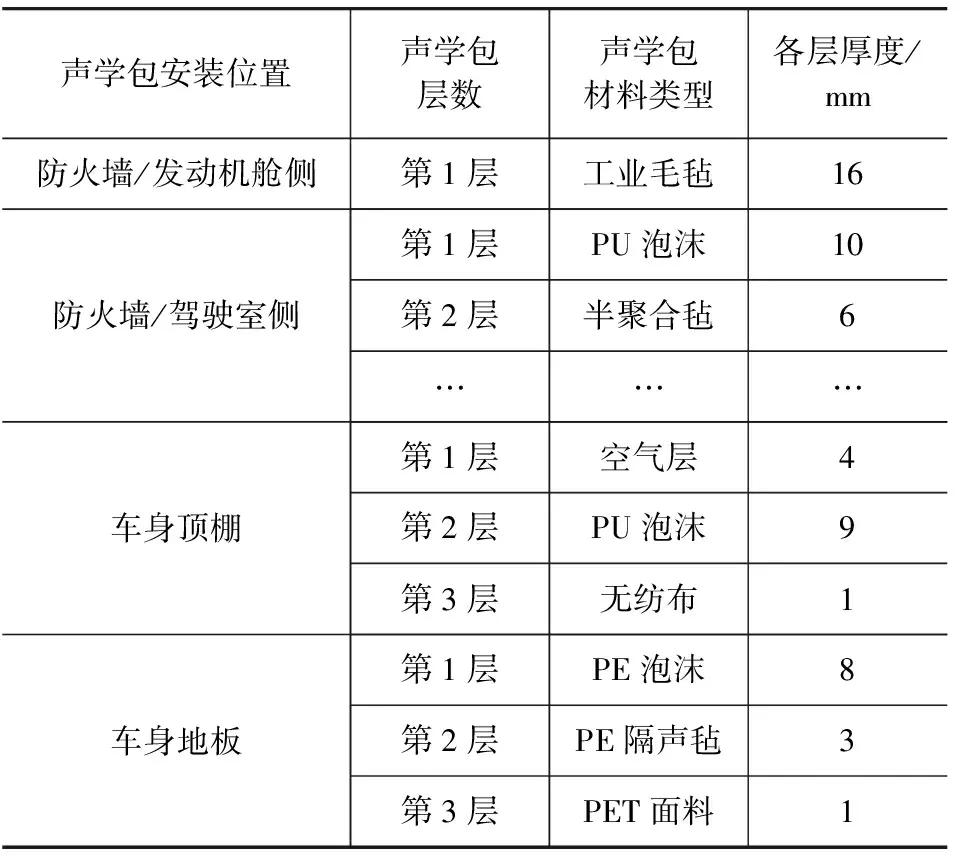
表2 整车各子系统声学包

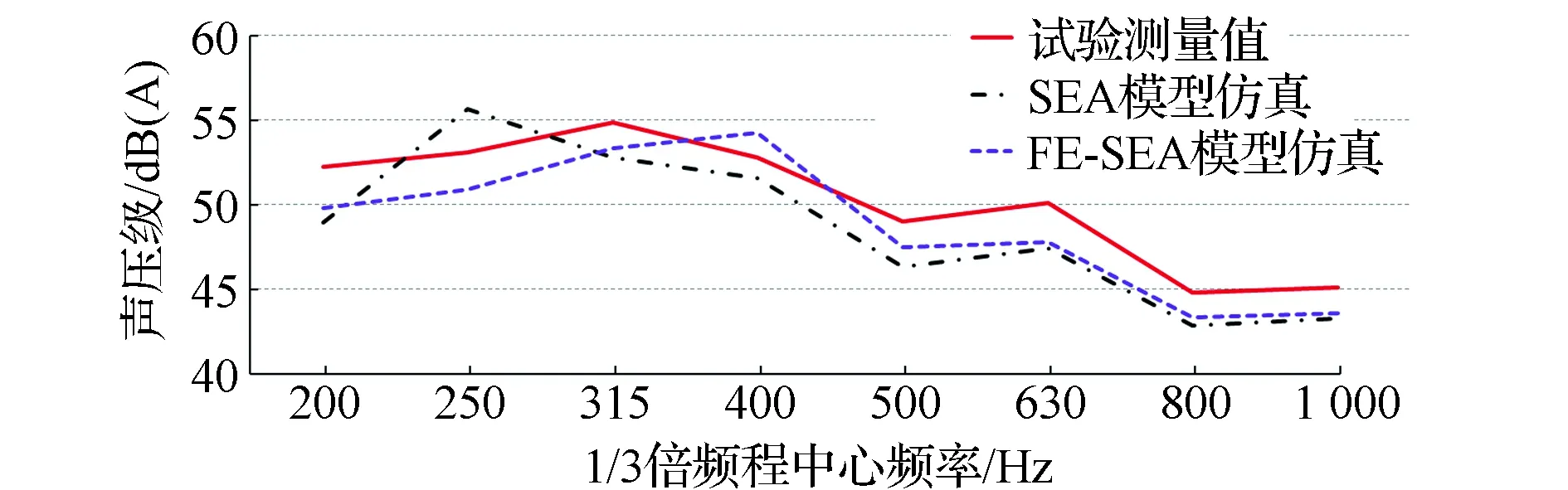
图11 预测值与测量值的对比曲线

4.3 车内中频噪声激励源分析

对混合FE-SEA模型分别只施加发动机舱声辐射激励和只施加各悬置点的振动激励进行仿真，结果如图12所示。由图可见，在680Hz以下，各悬置点的振动激励为主要车内噪声源；在680Hz以上，发动机舱声辐射激励为主要噪声源；且在整个中频范围内各悬置点的振动激励对车内噪声的总体贡献量要大于发动机舱声辐射激励。

表3 不同方法计算内损耗因子时混合FE-SEA模型的预测精度对比

图12 施加不同激励仿真结果对比曲线

5 结论

本文中对混合FE-SEA建模过程中的细节进行了总结，提出了混合建模应遵循的基本原则，为今后进行混合建模提供参考。

建立了轿车混合FE-SEA模型和SEA模型，在50km/h匀速工况下，将预测值分别与试验测量值进行对比。结果表明，中频范围内混合FE-SEA模型的预测精度要高于SEA模型。对比了使用不同计算方法得到的内损耗因子对混合FE-SEA模型预测精度的影响。结果表明，使用能量注入法可以提高中频段混合模型的预测精度。对混合FE-SEA模型施加不同种类的激励进行仿真计算，发现车内中频噪声的主要激励源随频率的变化而不同，且在整个中频范围内各悬置点的振动激励对车内噪声的总体贡献量要大于发动机舱声辐射激励,该仿真结果可对车内中频噪声采取降噪措施时提供一定的指导。

[1]CHUANGChing-Hung,SHUKun-Tien,LIUWei,etal.ACAEOptimizationProcessforVehicleHighFrequencyNVHApplications. [C].SAEPaper2005-01-2422.

[2]GREENIS.Vibro-AcousticFEAnalysisoftheSAAB2000Aircraft[C].Proceedingsofthe4thNASA/SAE/DLRAircraftInteriorNoiseWorkshop-NASAConference, 1992: 47-69.

[3]LANGLEYRS,BremnerP.AHybridMethodfortheVibrationAnalysisofComplexStructural-acousticSystems[J].JournaloftheAcousticalSocietyofAmerical, 1999,105(3):1657-1671.

[4]SHORTERPJ,LANGLEYRS.Vibro-acousticAnalysisofComplexSystems[J].JournalofSoundandVibration,2005, 288(3): 669-699.

[5]YANHH,PARETTA.AFEA-basedProceduretoPerformStatisticalEnergyAnalysis[C].SAEPaper2003-01-1553.

[6]ArnaudCharpentier,PrasanthSreedhar,BryceGardner,etal.UseofaHybridFE-SEAModelofaTrimmedVehicletoImprovetheDesignforInteriorNoise[C].SAEPaper2009-01-2199.

[7]ArnaudCharpentier,KazukiFukui.UsingtheHybridFE-SEAModelofaTrimmedFullVehicletoReduceStructureBorneNoisefrom200Hzto1kHz[C].SAEPaper2011-26-0020.

[8] 陈书明,王登峰,曹晓琳,等.车内噪声FE-SEA混合建模及分析方法[J].振动工程学报,2010,23(2):140-144.

[9] 陈书明,王登峰,昝建明.基于FE-SEA混合模型的轿车车内噪声预测[J].汽车工程,2011,33(3):236-240.

[10] 姚德元,王其政.统计能量分析原理及其应用[M].北京：北京理工大学出版社,1995.

[11] 宋继强,王登峰,马天飞，等.汽车车身复杂子结构模态密度确定方法[J].吉林大学学报，2009,39(2):270-271.

[12] 王彬星.重型汽车车内声压级预测与主要噪声源分析[D].北京：清华大学,2013.

[13] 朱磊. 轿车车内噪声控制的统计能量分析法[D].长春：吉林大学，2007.

FE-SEA Hybrid Analysis on the Interior Middle Frequency Noise of a Passenger Car

He Yansong1,2, Zhang Hui2, Xia Xiaojun2, Xu Zhongming1,2& Zhang Zhifei1,2

1．ChongqingUniversity,TheStateKeyLaboratoryofMechanicalTransmission,Chongqing400030； 2．CollegeofAutomotiveEngineering,ChongqingUniversity,Chongqing400030

Both FE-SEA hybrid model and SEA model for a car are established respectively and the modal density, internal loss factor and coupling loss factor of each subsystem are calculated. The sound radiation excitation of engine compartment, the excitation of powertrain mounting points and the excitation of road roughness to car body suspension points are measured by test at constant speed of 50km/h. The sound pressure level at driver's right ear is predicted with both FE-SEA hybrid model and SEA model respectively, and compared with test results, indicating that at the whole middle frequency range of 200-1,000Hz, the prediction accuracy of FE-SEA hybrid model is higher than that of SEA model. Then the internal loss factors calculated by power injection method are input to FE-SEA hybrid model for recalculation. The results show that the prediction accuracy is further improved at middle frequency range. Finally, the vibration excitation of suspension points and the sound radiation excitation of engine compartment are applied to FE-SEA hybrid model respectively to calculate and analyze the main excitation source of in-car noise at different frequency bands.

middle frequency noise; FE-SEA hybrid model; power injection method; prediction

*国家自然科学基金(51275540)和重庆市研究生科研创新项目(CYB14036)资助。

原稿收到日期为2015年3月26日，修改稿收到日期为2015年12月3日。