花纹结构对轮胎滚动噪声影响的研究*

项大兵,危银涛,冯希金

(清华大学汽车工程系,北京 100084)

2016119

花纹结构对轮胎滚动噪声影响的研究*

项大兵,危银涛,冯希金

(清华大学汽车工程系,北京 100084)

本文中发展了混合拉格朗日-欧拉(MLE)方法以对重载子午线轮胎的冲击振动噪声进行仿真。结合室内近场噪声试验，建立了冲击振动噪声在轮胎滚动噪声中所占比重的分析方法。通过对3款不同花纹结构的轮胎进行冲击振动噪声和滚动噪声的对比分析，找出了轮胎冲击振动噪声在轮胎滚动噪声中所占比重与轮胎花纹主要结构参数的关系。结果表明，对于块状花纹重载子午线轮胎，冲击振动噪声是总滚动噪声的主要成分，可使用MLE方法进行噪声分析与改进。而对于混合花纹和条状花纹，冲击振动噪声所占比重较小。

前言

轮胎是汽车中非常重要的噪声源之一，尤其是汽车行驶速度达到70km/h以上时，轮胎噪声占据了汽车噪声的主要成分[1-3]。因此降低轮胎噪声已成为降低汽车噪声的重要目标。世界各国相继出台了专门的轮胎噪声限制法规，尤其是欧盟于2012年开始实施的轮胎标签法对轮胎噪声水平提出了更加苛刻的要求。面对日益严苛的法规环境，研究轮胎降噪技术、开发低噪声绿色环保轮胎是摆在学术界和企业界面前的一项紧迫任务。

轮胎噪声的产生机理非常复杂，主要包括了与空气动力相关的泵浦噪声、空气柱共鸣噪声、赫姆霍兹共振噪声、空气紊流噪声以及与振动相关的胎面冲击振动噪声、花纹块粘滑振动噪声和粘吸振动噪声[4]。遗憾的是，目前业界对各种噪声机理所占的比重却没有一个准确的定论。由于缺乏有效的试验方法来单独测量轮胎噪声中的某一成分，故对轮胎噪声机理的研究通常采用理论解析的方法得出若干半经验理论公式，或采用非常简化的轮胎模型来进行噪声仿真[5-13]。然而，这些方法在实际运用中很难处理复杂花纹的轮胎，因此研究轮胎花纹结构对噪声的影响十分困难。

本文中发展了混合拉格朗日-欧拉(MLE)方法[14]用于重载子午线轮胎(指载货车和大客车用子午线轮胎)冲击振动噪声仿真，对几款不同花纹结构的轮胎进行了噪声研究。并结合近场噪声试验结果，找出了重载子午线轮胎花纹结构对轮胎滚动噪声影响的一般规律和这种影响的作用机理，为低噪声轮胎花纹设计提供了有效的参考依据。

1 理论基础

1.1 轮胎滚动动力学分析

本文中采用作者提出的混合拉格朗日-欧拉(MLE)方法在拉格朗日体系下分析滚动轮胎表面的振动加速度。轮胎滚动动力学包含大变形和有限转动，对于这种问题的求解，拉格朗日体系具有如下优点：质量矩阵和刚度矩阵都对称，无科氏加速度(陀螺)效应，系统是正定的。从大变形问题的虚功原理出发推导了滚动轮胎的动力学方程：

∫VδuIbIdV-∫ΓδuItIdΓ=0

(1)

式中Π,uI,c,EIJ,SIJ,bI和tI分别是总势能、相对于初始构形的总位移、阻尼系数、格林应变张量，第二类Piola-Kirchhoff应力张量、体应力和边界上的应力。

欧拉坐标和格林应变分别表示为

(2)

用有限元方法的节点插值坐标和插值位移表示为

(3)

位移导数可以表示为

(4)

则格林应变与位移之间的关系可用应变矩阵B表示：

δE=Bδuα

(5)

离散的虚功原理可以表示为

∫VBTSdV-∫VNibIdV-∫ΓNItIdΓ]=

(6)

据此可以得到动力学控制方程为

(7)

式中：M为质量矩阵；C为阻尼矩阵；P(u)为弹性内力矢量；F为外力矢量。显示求解过程可以用如下预测-校正原理来描述。

首先设定初始位移、速度并计算出加速度：

(8)

式中u0,v0和a0分别为位移、速度和加速度分量。

第n+1时间步的位移和速度可以根据n步先预测:

(9)

式中：β,γ为数值常数，一般可以取为0.25和0.5；Δt为时间步长。

由式(10)求解得到拉格朗日节点上的加速度信息。

(10)

在Abaqus中计算得到的轮胎表面节点加速度和位移信息是在随轮胎滚动的拉格朗日网格中，并不能直接作为声学有限元计算的振动边界条件[15-16]。因此需要使用MLE方法对加速度进行网格映射，将跟随轮胎滚动的拉格朗日网格上的加速度信息映射到空间固定的欧拉网格上，从而为声学有限元计算提供完整的振动辐射边界条件。

由于轮胎发生滚动变形，欧拉网格上的节点并不完全处于拉格朗日单元所在平面上，即二者的位置关系是空间几何关系，所以不能直接对节点上所含有的信息进行有限元插值。因此在进行单元识别和数据插值之前，需要对两种网格上的节点进行坐标变换，从整体坐标系变换到每一个拉格朗日单元所在平面的局部坐标系上。

空间节点坐标变换示意图如图1所示。在整体坐标系O-xyz中，拉格朗日单元e由节点1,2,3,4组成；点p为欧拉网格上的任意一个节点；点p′为点p在单元e所在平面内的投影点。O′-uvw是建立在拉格朗日单元所在平面上的局部坐标系。

图1 空间节点坐标变换示意图

下面以拉格朗日单元的中心O′点为原点，以直线O′1方向为坐标轴u的正方向，推导局部坐标系的坐标阵，从而得到坐标变换矩阵。

局部坐标系的坐标阵为H=(u,v,w)。其中u,v,w分别为局部坐标系的3个坐标轴的方向向量，可以由单元所在平面内任意两条相交向量以及平面的法向量n正交化得到。取单元中心点O′和单元节点1,2的连线构成一组平面内的相交向量，记为α,β。单元平面的法向量n可用向量α,β的叉积表示为n=α×β。取向量u=α/|α|,w=n/|n|,v=w×u。则H=(u,v,w)构成了单元局部坐标阵。点p的局部坐标可通过其整体坐标和单元局部坐标阵的逆矩阵求得。

通过坐标变换，将空间中的任意欧拉节点p投影到拉格朗日单元e上得到p′点坐标。然后利用p′点对欧拉节点和拉格朗日单元进行配对。

图2 向量形式下的节点与单元关系

假设拉格朗日单元是四边形单元，其4个节点按逆时针顺序排列。当平面中的欧拉点p处于单元内部时(如图2(a)所示)，则称该拉格朗日单元属于欧拉节点。

一个四边形单元可以分解成4个首尾相连的平面向量(如图2(b)所示)。如果一个拉格朗日单元属于此欧拉节点，那么该欧拉节点应处于所有向量的左侧。即节点p与上述4个向量具有相同的数学关系。下面通过其中一个向量确定这种数学关系，并作为拉格朗日单元识别的判据。

记节点1到2的向量为a,点1到p的向量为b,如图2(b)所示，如果点p在向量a的左侧，那么向量a到向量b的角θ满足不等式0<θ<1800。因此向量a和b的叉积c大于零，即

c=a×b>0

(11)

因此，对于一个拉格朗日单元，当所有向量均满足式(11)不等式时，则判定该拉格朗日单元属于欧拉节点p。

对于某个欧拉节点p，若已经判断其所属的拉格朗日单元为e，则可对其进行信息映射。

拉格朗日单元上的插值坐标系如图3所示，点p为完成坐标变换后的欧拉点，1,2,3,4为拉格朗日单元的4个节点。点A,B,C,D分别是四边形单元每条边的中点。点O是线段AC和BD的交点。以点O为原点，在单元上创建一个插值坐标系O-ζη。以直线OB和OC的方向为插值坐标系的坐标轴方向，插值坐标系的坐标矩阵I可以表示为I=(ζ,η)，则平面内任意节点的插值坐标(ζi,ηi)可以表示为

(12)

式中：(xi,yi)为任意点的平面坐标；(xo,yo)为插值坐标系原点的平面坐标；I-1为I的逆矩阵。将式(12)代入式(13)中，即可求出单元中所有拉格朗日节点的插值形函数：

Ni=(1+ξiξp)(1+ηiηp)/4,i=1,2,3,4

(13)

图3 拉格朗日单元上的插值坐标系

形函数确立以后，拉格朗日网格和欧拉网格中的加速度映射关系可通过下式唯一确定：

(14)

式中：ap为映射到欧拉网格上的振动加速度；ai为映射前的振动加速度。

2 轮胎冲击振动噪声仿真方法

轮胎振动噪声仿真主要包含以下3个流程：(1)复杂花纹轮胎的无缝建模；(2)拉格朗日-欧拉体系下的信息映射；(3)轮胎冲击振动噪声的有限元仿真。

2.1 轮胎花纹的无缝建模

为反映轮胎与路面之间真实的作用机理，提取有效的胎面振动加速度数据。需要建立准确的轮胎三维模型,该模型必须具有完整的胎面花纹结构。由于在轮胎振动噪声的仿真过程中，花纹沟和花纹块的外表面都同时作为轮胎的胎面振动声源，因此在轮胎模型建立的过程中需要将轮胎的花纹沟和花纹块作为同一个结构进行整体建模，使轮胎三维有限元网格中的花纹块与花纹沟之间完全由共节点单元组成。然后将花纹模型贴合到去除胎面的轮胎三维模型上，从而实现胎面花纹与轮胎结构之间的无缝连接。而且这种建模方式还为后续的轮胎胎面加速度的导出提供了便利。建模过程如图4所示。

图4 复杂花纹的三维轮胎模型建立方法

轮胎三维模型建立后，利用Abaqus中的显式有限元算法对轮胎三维模型进行滚动动力学分析，导出轮胎表面节点的振动加速度和位移(空间坐标)信息。基于Fortran语言编制MLE数据映射程序，完成加速度信息从拉格朗日网格向欧拉网格之间的映射,为轮胎的冲击振动噪声仿真提供稳定的加速度边界条件。图5(a)和图5(b)分别给出了轮胎表面某节点在0-0.2s的时间内空间坐标和加速度映射前后的分布。为清楚展示拉格朗日节点运动情况，此处仅选取10个计算步的数据，采样间隔为0.02s，而实际计算步长为0.000 4s。数据映射的目的是消除轮胎刚体滚动效应。

图5 轮胎表面某节点坐标和加速度映射结果

从图5(a)中可以明显看出，数据映射之前的节点随时间的变化形成近似圆形的运动轨迹，反映了拉格朗日体系下轮胎表面节点随轮胎滚动这一事实。所有的轮胎表面节点组成了一系列的旋转声源，这既不符合轮胎噪声来源于接地区域附近的事实，也由于拉格朗日声源和欧拉噪声网格之间的不协调而难以数值实现。处理之后的观察点从轮胎表面转移到轮胎所在的空间上，不随轮胎的运动而运动，此时空间观察点上的加速度信息由当前时刻附近的轮胎节点上的加速度插值得到。

最后，将所有节点信息映射完成以后，则可得到空间固定的欧拉网格上的加速度信息，为轮胎振动噪声仿真提供了“稳定”的加速度边界条件，这里的“稳定”是指网格节点在空间中是稳定不转动的，但是网格上的加速度是随时间变化的。图6给出了映射后的轮胎表面振动加速度分布云图，从中可以明显看出轮胎接地区域附近的胎面振动最为强烈。

图6 映射后的轮胎表面振动加速度分布云图

2.3 轮胎的振动噪声计算

得到空间固定的轮胎表面振动加速度辐射边界条件以后，在LMS.Virtual.Lab平台上，利用声学自动匹配层(automatic matched layer, AML)技术对轮胎进行振动噪声计算。其中AML技术是在声学完美匹配层(perfect matched layer, PML)技术基础之上发展而成的一种高级声学有限元技术[17-20]。

图7给出了某款轮胎的噪声仿真云图和频谱曲线图。其中场点网格的布置与近场试验时传声器位置相同，图7(a)中A点在测量区域的前端，B点在测量区域的后端。从图7(a)中可以明显看出B点的声压要大于A点，而且测量区域后端的高噪声区域要明显大于测量区域前端，这一结果与试验结果相符合。图7(b)是场点网格中A点处的噪声频谱图。

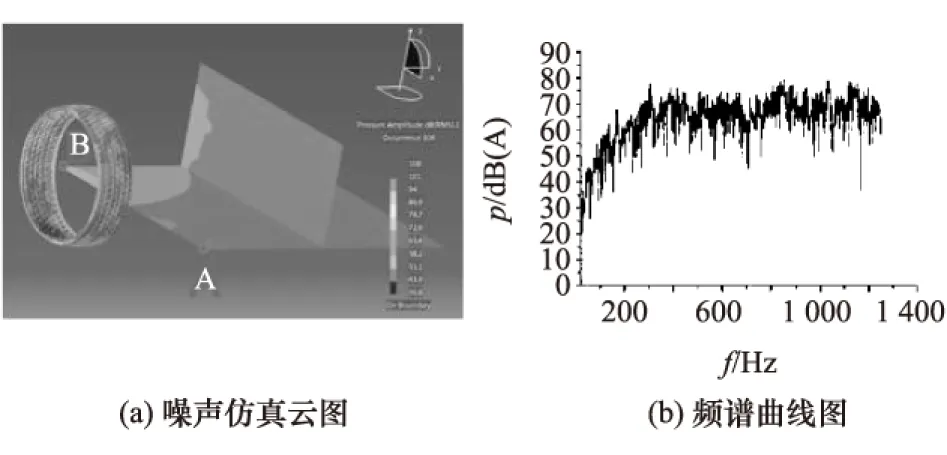
图7 某款轮胎噪声仿真云图和频谱曲线图

3 花纹结构对轮胎振动噪声的影响

3.1 轮胎振动噪声试验

轮胎振动噪声仿真时轮胎是在转鼓的驱动下进行滚动的，而且轮胎中心并没有发生平移运动。为了保持试验与仿真工况的一致，本文中使用轮胎近场噪声试验结果与仿真结果进行对比。近场噪声试验在半消声室内完成，试验照片如图8(a)所示。以轮胎接地中心为圆心、1m为半径的半圆弧上分别放置9个传声器，位置如图8(b)所示。试验方案详见文献[21]。

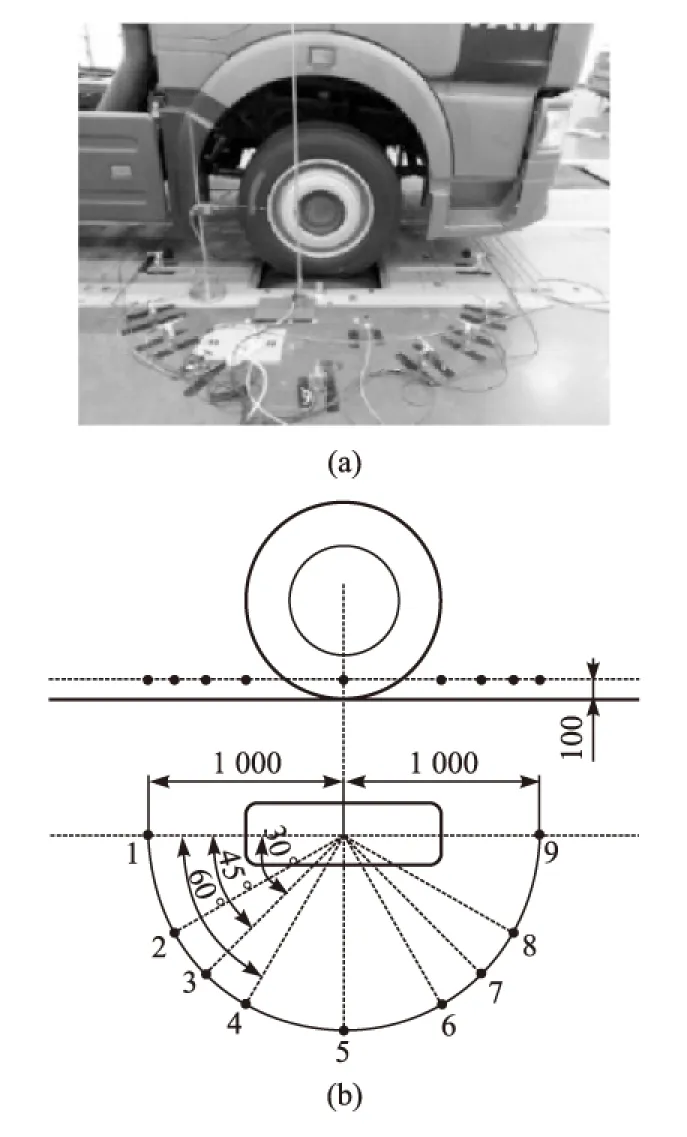
图8 轮胎近场噪声试验传声器布置图

3.2 仿真与试验结果的对比

用上述方法分别对不同花纹的3款重载子午线轮胎进行了噪声仿真和试验研究。3款轮胎的花纹如图9所示，分别为具有代表性的块状花纹结构、混合花纹结构和条状花纹结构。仿真时轮胎载荷和气压与试验时保持一致，轮胎滚动速度为70km/h。

图9 3种不同轮胎的花纹结构图

图10给出了噪声频谱曲线的试验与仿真的结果对比。试验结果为图8中的第8号传声器的采集数据，传声器位置如下：离轮胎中心距离1m，与轮胎前进方向夹角为30°，高度为100mm。仿真结果取自场点网格中的节点A，其空间位置与上述传声器位置相同。

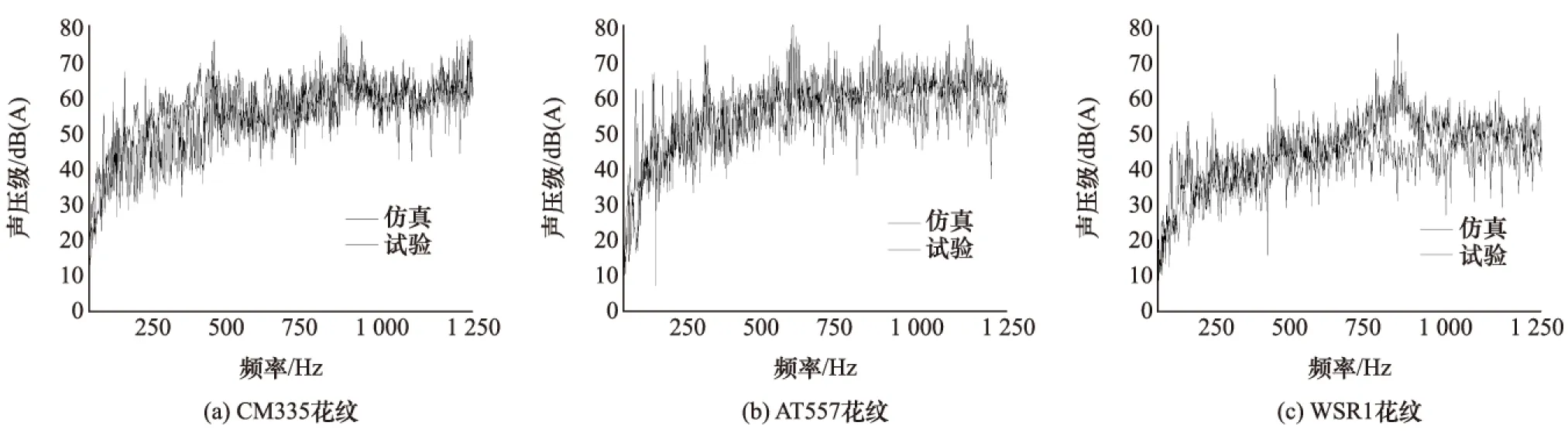
图10 仿真与试验频谱曲线对比图

从图10中可以明显看出，对于CM335和AT557型花纹轮胎，在1-1 250Hz内，轮胎冲击振动噪声频谱曲线与试验频谱曲线趋势一致，吻合较好，而对于WSR1型轮胎花纹，在低频阶段(0-600Hz)轮胎振动噪声仿真频谱曲线能够很好地与试验结果吻合，但是在高频阶段尤其是800Hz左右误差较大，试验结果明显高于仿真结果，说明了在这个频率附近存在某一个未知的与轮胎冲击振动机理无关的声源在起作用。

图11给出了3种花纹轮胎噪声结果的1/3倍频程图。从图11(a)中可以明显看出在各个频段，冲击振动噪声仿真结果与滚动噪声试验结果能量分布非常相似。从而充分说明了对于CM335轮胎，冲击振动是轮胎噪声的主要声源，并对该款轮胎总声压级起了决定性作用。降低该款轮胎冲击振动噪声是降低总声压级的有效方法。从图11(b)和图11(c)中可以看出，对于AT557和WSR1型花纹轮胎，低频阶段冲击振动为轮胎噪声提供了大部分的声能量，但是在高频阶段，试验结果明显高于仿真结果。说明在这一频段，与气流和摩擦有关的噪声对噪声总能量也有较大贡献。

表1为不同花纹轮胎噪声仿真结果与试验结果

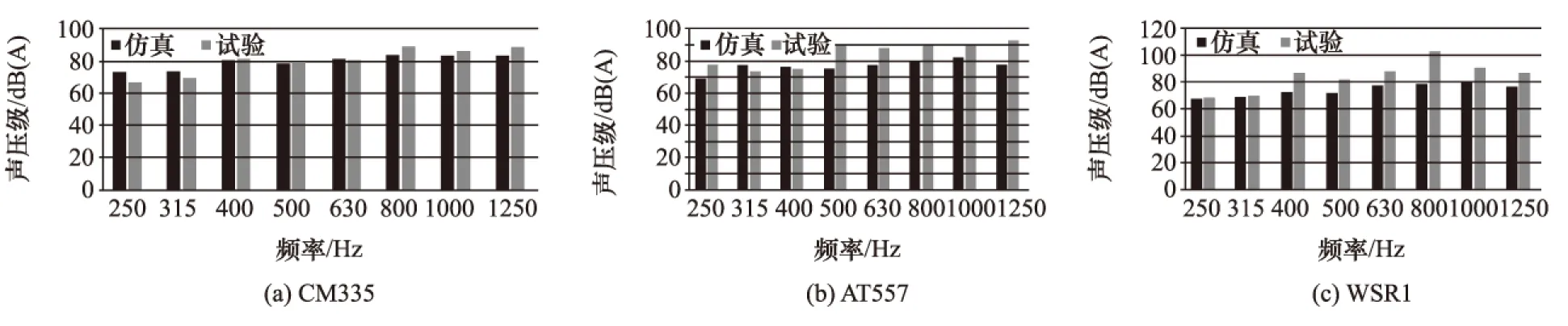
图11 仿真与试验1/3倍频程对比图

及其误差的对比。由于3款轮胎花纹结构不同，冲击振动噪声所占比重不同。因而对于3款花纹结构的轮胎，冲击振动噪声仿真结果与试验整体综合噪声结果误差不同。误差主要来源于其他噪声机理的作用。

表1 试验与仿真声压级对比表 dB(A)

3.3 轮胎噪声与花纹结构关系的研究

3款仿真轮胎主要花纹结构参数如表2所示。

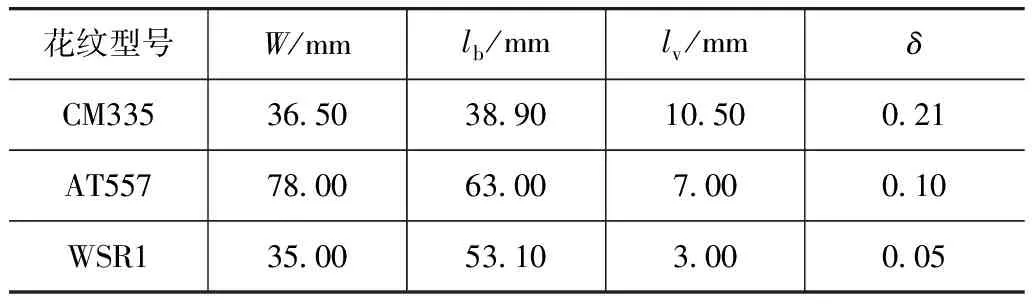
表2 3款轮胎花纹的结构参数

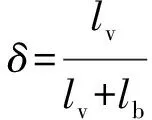
结合3款花纹轮胎的图片和花纹结构参数，可以看出从花纹型号CM335，AT557到WSR1，花纹的形状因子依次减小，花纹块接地时的冲击振动依次减弱，所以冲击振动噪声所占总噪声比重依次下降。其中CM335花纹完全属于块状驱动花纹类型，冲击振动噪声仿真结果与试验噪声结果误差小于1dB(A)，因此可以使用冲击振动噪声来估算整体噪声，并忽略其他噪声成分。而对于WSR1型花纹，属于典型的条状花纹，冲击振动噪声仿真结果和试验结果误差高达15dB(A)，这说明对于条状花纹，轮胎冲击振动噪声只占据了其中较小的部分。对于AT557型混合花纹此项比重则介于二者之间。

实际上，对于上述3种花纹轮胎，由噪声声压级叠加公式可以近似估算出空气泵浦噪声和其他噪声成分。估算公式如下：

L0=10log(100.1Lp-100.1Lvib)

(15)

式中：Lp为轮胎噪声整体声压级，在这里用近场噪声试验值代替轮胎整体声压级；Lvib为冲击振动噪声分量；L0为冲击振动以外机理引起的噪声部分。根据上述公式计算出的不同机理引起的噪声声压级结果如表3所示。

表3 不同噪声成分声压级对比表 dB(A)

从表3中可以明显看出，不同轮胎花纹的噪声成分区别很大。对于CM335型大块状花纹，冲击振动噪声远大于其他噪声成分。然而对于AT557和WSR1型花纹，其他噪声要远大于冲击振动噪声。

4 结论

采用发展的混合拉格朗日-欧拉(MLE)方法对复杂花纹轮胎冲击振动噪声进行有限元仿真，并将仿真结果与近场试验结果进行对比，分析了不同花纹轮胎冲击振动噪声的比重，结论如下。

(1) 混合拉格朗日-欧拉方法可对轮胎冲击振动噪声进行仿真，对于块状驱动花纹结构的重载子午线轮胎冲击振动噪声与试验结果吻合的很好。

(2) 轮胎花纹的结构形式直接影响了其冲击振动噪声在整体滚动噪声中所占比重，其中对于块状驱动花纹轮胎，冲击振动噪声占据主要成分，而对于混合花纹和条状花纹轮胎，冲击振动噪声的贡献较小。

(3) 对于重载子午线轮胎，如果其花纹为驱动花纹且花纹沟具有较大的宽度、花纹块具有较大的体积和花纹形状因子较大，则其冲击振动噪声占据了主要成分。

本文的研究证明作者发展的混合拉格朗日-欧拉方法能够有效地仿真滚动轮胎的冲击振动噪声。为低噪声轮胎的分析与设计提供了可行的方法。

[1] SANDBERG U, DESCORNET G. Road surface influence on tire/road noise[C]. Inter-Noise 80. Noise Control for the 80’s. Proceedings of the 1980 International Conference on Noise Control Engineering,1980:259-266.

[2] SANDBERG U, EJSMONT J A. Basic methods for measurement of tire-road noise[J]. Noise Control Engineering Journal,1984,23(3):98-98.

[3] SANDBERG U, EJSMONT J A.Tyre/road noise reference book[M]. Informex. Kisa. Sweden,2002:202-227.

[4] Tyre/road noise models in the last two decades: a critical evaluation[C]. The 2001 International Congress and Exhibition on Noise Control Engineering, The Hague, The Netherlands,2001 August 27-30.

[5] DUBOIS G, CESBRON J, YIN H P, et al. Statistical estimation of low frequency tyre/road noise from numerical contact forces[J]. Applied Acoustics,2013,74:1085-1093.

[6] LOPEZ I, BLOM R E A, ROOZEN N B, et al. Modelling vibrations on deformed rolling tires-a modal approach[J]. Journal of Sound and Vibration,2007,307:481-494.

[7] BRINKMEIER Maik. A finite element approach for the simulation of tire rolling noise[J]. Journal of Sound and Vibration,2008,309(2-1-2):20-39.

[8] BERCKMANS D, KINDT P, et al. Evaluation of substitution monopol models for tire noise sound synthesis[J]. Mechanical Systems and Signal Processing,2010,24:240-255.

[9] O’BOY D J, DOWLING A P. Tyre/road interaction noise-numerical noise prediction of a patterned tyre on a rough road surface[J]. Journal of Sound and Vibration,2009,323:270-291.

[10] 刘聚德,陈志芳.轮胎垂直振动动力学模型[J].汽车工程,1993,15(5):263-267.

[11] 于增信.轮胎噪声机理与仿真研究[D].哈尔滨:哈尔滨工业大学,2001.

[12] 陈理君,魏波涛.非小块状轮胎花纹噪声仿真试验模型[J].轮胎工业,2006,26(2-12):718-722.

[13] 包秀图,张涛,李子然,等.轮胎振动噪声的数值模拟[J].振动与冲击,2008,11(27):6-11.

[14] 冯希金,危银涛,项大兵,等.基于MLE方法的滚动轮胎冲击振动噪声仿真分析[J].噪声与振动控制,2015,35(4).

[15] OERTEL C, WEI Y. Tyre rolling kinematics and prediction of tyre forces and moments: part I-theory and method[J]. Vehicle System Dynamics,2012,50(11):1673-1687.

[16] WEI Y, OERTEL C, SHEN X. Tyre rolling kinematics and prediction of tyre forces and moments: part II-simulation and experiment[J]. Vehicle System Dynamics,2012,50(11):1689-1706.

[17] 詹福良,徐俊伟.Virtual.Lab Acoustics声学仿真计算从入门到精通[M].西安:西北工业大学出版社,2013:6-9.

[18] HU F Q. A stable perfectly matched layer for linearized euler equations in unsplit physical variables[J]. Journal of Computational Physics,2001,173(2):455-480.

[19] ATASSI O V. Nonreflecting boundary conditions for the time-dependent convective wave equation in a duct[J]. Journal of Computational Physics,2004,197:737-758.

[20] HU F Q. Development of PML absorbing boundary conditions for computational aeroacoustics: a progress review[J]. Computers & Fluids,2008,37(4):336-348.

[21] 陈亚龙.C3轮胎通过噪声的室内外对比研究[D].北京:清华大学,2014.

A Study on the Influence of Tread Structure on Tire Rolling Noise

Xiang Dabing, Wei Yintao & Feng Xijing

DepartmentofAutomotiveEngineering,TsinghuaUniversity,Beijing100084

In this paper, mixed Lagrange-Euler (MLE) method is extended to simulate the vibration noise of truck and bus radial (TBR) tires. Combined with in-door near field noise tests, an analysis method of the proportion of vibration noise in the total rolling noise of tire is established. By a comparative analysis on the vibration noise and total rolling noise of three TBR tires with different tread patterns, the relationship between the proportion of vibration noise in total rolling noise and the main structural parameters of tire pattern is found. The results show that for a TBR tire with block treads, its vibration noise dominates the main components of rolling noise and can be analyzed and improved by MLE method, while for a tire with ribbed and compound treads, the proportion of vibration noise in total rolling noise is relatively small.

tire tread structure; vibration noise; mixed Lagrange-Euler method

*国家自然科学基金(51275265，51175286)资助。

原稿收到日期为2015年4月10日，修改稿收到日期为2015年5月24日。