一种基于最优多项式模型的车身耐撞性敏感性分析法*
2016-04-17刘光昭于钟博
刘 杰,刘光昭,许 灿,于钟博
(湖南大学机械与运载工程学院,汽车车身先进设计制造国家重点实验室,长沙 410082)
2016109
一种基于最优多项式模型的车身耐撞性敏感性分析法*
刘 杰,刘光昭,许 灿,于钟博
(湖南大学机械与运载工程学院,汽车车身先进设计制造国家重点实验室,长沙 410082)
为评价车身耐撞性对结构参数的敏感性,提出了一种基于最优多项式模型的新型全局敏感性分析方法。通过误差减少比率的结构选择技术构造了描述耐撞性指标和结构设计参数之间关系的最优多项式模型,并利用基于直接积分的Sobol方法进行全局敏感性分析。该方法克服了传统方法计算量大、结果不稳定等缺点,车辆正撞和侧撞工程算例的敏感性分析结果表明了该方法的有效性和实用性。
车身耐撞性;全局敏感性;最优多项式;Sobol方法
前言
结构敏感性分析通过分析各设计参数与设计目标之间的变化规律,并以敏感性指标为基准对车身各结构参数的影响程度进行有效排序和评估[1],这对于提高车身产品的设计效率,缩短设计周期,快速有效地确定结构修改方案有着重要意义和实际价值。
目前敏感性分析分局部和全局分析两大类方法[2]。局部敏感性分析方法[3-5]主要包括直接求导法、有限差分法和摄动法,其分析简单,但只能检验单个参数的变化对设计目标的影响程度,适用于线性模型且参数范围较小情况。全局敏感性分析方法[6-9]包括回归分析法、方差分析法、傅里叶幅值分析法和Sobol法,其参数变动范围可扩展到参数的整个定义域,允许多个参数同时变化,且不受模型的限制,但全局法往往通过采样技术来分析,其计算量较大。其中,Sobol法[10-11]是一种应用较广泛的全局敏感性分析方法,该方法基于方差分析,通过计算单个或多个设计参数对设计目标方差的贡献来评估各参数的敏感性,同时还能给出多个参数的交互作用对设计目标的影响。传统Sobol法通常采用蒙特卡洛采样进行求解[12-13],这需要大量的样本信息,且敏感性分析结果的稳定性严重依赖于样本。对于车身耐撞性设计这类复杂问题,单次有限元模拟计算就已经非常耗时,因此通过大量采样进行Sobol全局敏感性分析是很难实现的。虽然有些学者建立了设计参数与车身耐撞性指标之间的各类近似模型,再在近似模型的基础上进行基于蒙特卡洛采样的Sobol敏感性分析,这一定程度克服了计算量大的问题,但分析结果依然存在对样本的依赖性,尤其是对于高维变量的设计问题,近似模型的精度、采样的方法、样本量的大小等都可能使分析结果存在较大偏差,特别是对于高阶交叉项的敏感性分析存在较大的偏差和数值不稳定性。
为更有效准确地量化车身耐撞性设计中结构参数的敏感性指标,本文中提出了一种新型基于最优多项式模型的全局敏感性分析方法。该方法根据误差减少比率对耐撞性指标和设计参数之间的多项式结构进行寻优,这种最优多项式模型不仅结构简洁、近似精度高,而且非常适用于直接积分的Sobol敏感性分析。正撞和侧撞工况下的车身结构的全局敏感性分析结果验证了本文中方法的有效性和实用性。
1 车身耐撞性的Sobol敏感性分析
针对车身耐撞性设计问题,利用Sobol敏感性分析方法对关键设计参数进行识别和定量化评估时,可将耐撞性指标分解成单个设计参数和参数之间的正交函数组合,即
f12…n(x1,x2,…,xn)
(1)
式中:x为n维设计参数向量;f(x)为耐撞性指标,如最大侵入量、加速度峰值等。
式(1)右边共有2n项,若除常数项f0外,各子项满足对其包含的参数积分为零,即

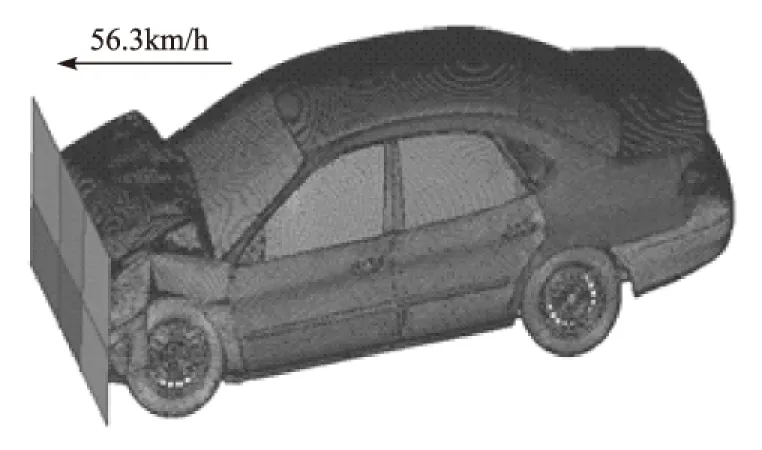
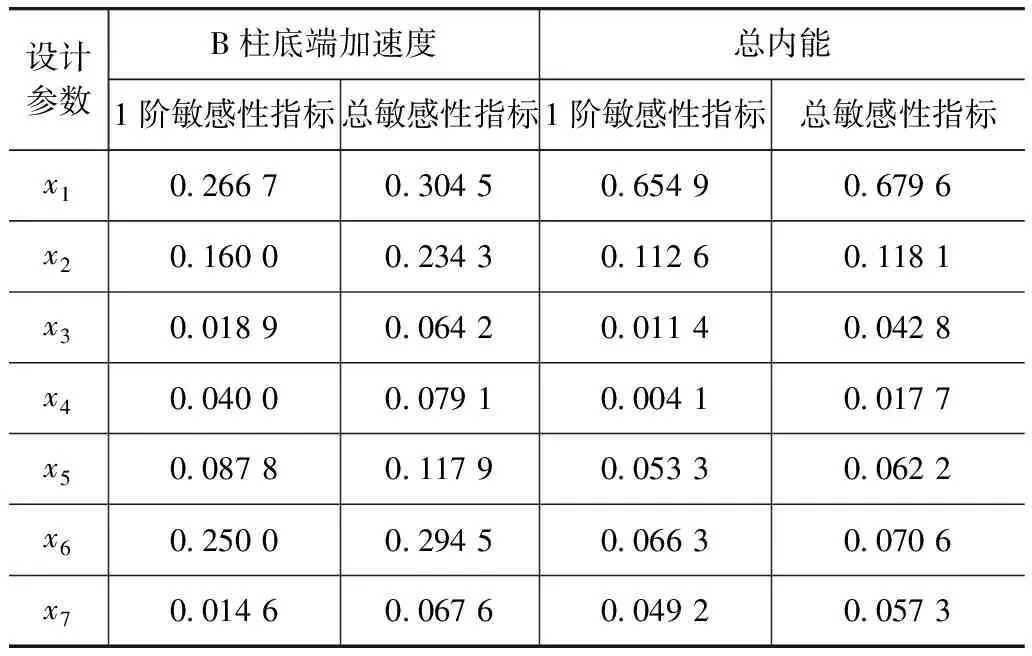
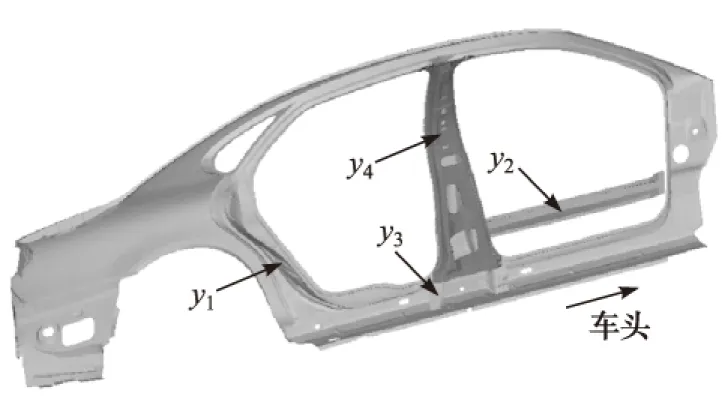
1≤i1<… (2) 则式(1)可唯一分解,且各项可通过下列多重积分求得 f0=∫f(x)dx (3) (4) (5) 同理可求得各阶高次项f12…k(x1,x2,…,xk)。 Sobol敏感性分析法通过偏方差和总方差之比来表示设计参数及其交互作用对耐撞性指标的影响程度[10-11],其中耐撞性指标f(x)的总方差D为 (6) 式(1)中各项的偏方差Di1…is为 (7) 对式(1)两边先平方再积分,并由各项正交的性质可得 (8) 则式(1)中各项的敏感性指标Si1i2…is为 Si1i2…is=Di1i2…is/D (9) 单个设计变量xi的总敏感性指标TS(xi)为 TS(xi)=1-S-i (10) 式中S-i为不包含变量xi的所有Si1i2…is项之和。 Sobol敏感性分析方法在构造正交函数和计算方差的式(3)~式(7)中,都涉及多重积分的计算,传统是利用蒙特卡洛法进行求解。由于蒙特卡洛积分的准确性和稳定性往往取决于抽样的规模和均匀性,因此这将导致一方面对于车辆碰撞这类复杂工程问题,其计算量太大;另一方面对于高维设计变量问题,其敏感性分析结果不够准确。如果能构造出耐撞性指标和高维设计变量之间的较准确且便于直接积分的近似模型,则基于直接积分进行Sobol敏感性分析,能有效提高敏感性分析的效率和精度。 在利用各类响应面对车辆耐撞性进行Sobol敏感性分析时,多项式响应面非常适合直接积分计算。为在高维设计向量下较准确地替代耗时的模型仿真,下面采用误差比例结构选择技术[14-15]构造耐撞性指标和结构设计参数之间的最优多项式模型。 将耐撞性指标f(x)表示为n维设计参数的完全多项式组合,即 (11) 式中:ui为设计变量xi在m次方下的完全多项式;ai为待定多项式系数;多项式总项数为N=(n+m)!/(n!m!)。一般来说幂指数m可足够大,能包含全部有效的多项式项。多项式结构选择技术将对式(11)中每一项的显著性进行评估,并按照误差减小比率选择出有效的多项式项,从而获得耐撞性指标关于设计参数的最佳多项式模型。 为确定多项式模型及其系数,假定在n维设计参数空间进行L次抽样,并将式(11)的右边进行变换用正交集表示为 (12) 式中:f(k)为第k次抽样计算的耐撞性指标;pi(k)为第k次抽样下的正交项,由式(11)中各项经正交变换而得到;hi为正交项的系数。由于式(12)各项正交,故有 (13) pi(k)可以用Gram-Schmidt正交化得到 (14) (15) 式中:ui(k)为第k次抽样下式(11)中的各多项式;αij为系数。 在正交化过程中p0(k)=1。 定义误差函数MSE为 (16) 根据极值条件,式(16)右边表达式对hi求导,并令其等于0,可得 (17) 将式(17)代入式(16),并由pi(k)各项两两正交,可得 (18) (19) 每次正交变换后,计算各项对MSE减小的贡献率ERRi,选出误差减小比率最大的一项保留,剩余项重新按照上述方法做正交化处理并评价贡献率,直至剩余项中最大ERRi小于设定的阈值,则这些项可被舍弃。求解得到hi,再通过反正交变换可获得式(11)中保留项的系数为 (20) 式中:qi=1,且 (21) 由此可确定耐撞性指标关于设计参数的多项式模型的最佳结构及系数,在此基础上可方便地进行直接积分运算并评价各参数敏感性。 基于最优多项式模型和直接积分的Sobol敏感性分析法对车辆耐撞性进行全局敏感性分析的流程如图1所示,具体步骤为: 图1 直接积分全局敏感性分析流程 ①确定耐撞性指标、设计参数及其范围;②对设计参数进行实验设计,如利用拉丁超立方方法进行抽样;③计算仿真模型抽样点的耐撞性指标;④通过误差减少比率的结构选择技术构造了耐撞性指标和结构设计参数之间的最优多项式模型;⑤在最优多项式模型基础上,利用式(3)~式(5)进行直接积分,求得式(1)中各项;⑥对式(1)各项,利用式(6)和式(7)进行直接积分,求得总方差和偏方差;⑦利用式(9)和式(10)对各设计参数的各阶敏感性进行评价。 通过一个数值算例验证本文中所述方法的正确性和敏感性分析结果的准确性。数值算例的模型为 f(x)= 0.810-0.116x1+0.121x2+0.152x3+ (22) 式中:x∈[-1,1],其Sobol敏感性指标可以通过直接积分法得到。利用拉丁超立方法在x定义域内进行30次抽样,并代入式(22)求解函数值。为验证基于结构选择构造最优多项式模型的稳定性和准确性,在计算的函数值中加入10%水平的噪声,模拟实际测量或计算误差,带噪函数响应fδ为 fδ=fc+lδ·std(fc)·rand (23) 式中:fc为样本处计算的函数值;std(fc)为计算函数值的标准差;lδ为百分数,表示噪声水平;rand为均值是0,方差是1的随机数。利用样本点先建立完全多项式模型,进行结构选择,得到最优多项式模型: (24) 对比式(22)和式(24)可知,结构选择技术能选择出所有有效的多项式项,且具有很好的抗噪能力。表1列出本文方法和对式(22)进行不同规模蒙特卡洛抽样的敏感性指标计算结果,其中抽样Ⅰ和Ⅱ为不同批次下抽样5 000,抽样Ⅲ和Ⅳ为不同批次下抽样10 000。从表1结果可看出,基于蒙特卡洛方法的Sobol敏感性分析方法在不同抽样批次和规模下,其敏感性结果不稳定,特别是对于高阶敏感性指标其分析结果误差较大,而基于本文方法构造的最优多项式(24)与式(22)相近,因此对其进行直接积分的敏感性分析结果准确性较高。 表1 不同方法的敏感性分析对比 5.1 正撞工况车身结构的全局敏感性分析 建立某型车正面碰撞刚性墙有限元模型[16],如图2所示,碰撞速度为56.3km/h。车辆正撞时前端部件为主要变形吸能部件,因此选取该车前端7个部件的厚度作设计参数,这7个部件分别为左侧长纵梁x1、左侧子框架臂x2、前部子框架x3、左侧脚踏板梁x4、左侧防护罩x5、发动机内盖x6和发动机外盖x7,如图3所示。 图2 车辆正撞有限元模型(碰撞后100ms) 图3 车辆正撞的设计部件 选择左侧B柱底端加速度A和碰撞发生后总内能E作为车辆正面碰撞的耐撞性评价指标,利用拉丁超立方法进行50次抽样,并分别建立加速度a和总内能E的最优多项式模型: a= 55.80-6.55x1+6.39x2+5.15x3+0.59x4+ 0.34x1x3-0.46x1x4-3.00x1x5+2.01x1x6+ (25) E= 144.64+7.15x1+2.72x2+1.81x3+25.34x5- 0.77x1x3+0.20x1x4-0.64x1x5-0.33x1x6+ (26) 基于直接积分法进行Sobol敏感性求解,表2中列出了敏感性分析所得的各设计参数的1阶敏感性指标和总敏感性指标的值。 表2 正撞工况的全局敏感性分析结果 由表2可以看出,该车型在正碰工况下长纵梁、发动机内盖、子框架臂和防护罩对其B柱底端加速度影响较大,其余3个部件影响较小;对于碰撞总内能,长纵梁对其影响最大,在7个部件中占吸能比的60%以上,是车辆正面碰撞主要的吸能部件,这与长纵梁变形最大吸能最多的实际情况相符。通过正撞工况的敏感性分析结果,能有效筛选出对耐撞性指标影响较大的关键结构参数,从而为其优化设计提供指导。 5.2 侧撞工况车身结构的全局敏感性分析 建立某车侧撞工况下的有限元模型[17],如图4所示。碰撞速度为50km/h。当车辆受到侧面碰撞时,一方面变形较大的部位为车体左侧的框架、车门和B柱等,它们在侧撞中起着主要的吸能作用;另一方面可利用的缓冲吸能空间有限,又要求车门有足够的刚度,不应发生较大的变形。因此,在车辆侧撞工况的耐撞性设计中要兼顾碰撞吸能和侧面刚度两方面的需求。选取4个部件的厚度作为设计参数,即左侧一体式框架y1、侧前门加强筋y2、左侧B柱内板y3和外板y4,如图5所示。 图4 车辆侧撞有限元模型(碰撞后100ms) 图5 车辆侧撞的设计部件 选择B柱的最大侵入量U,B柱中部最大侵入速度v和非碰撞侧B柱下端加速度的第一个峰值M作为侧面碰撞的耐撞性指标,分别建立U,v和M的最优多项式模型: U= 349.90+18.03y1-95.32y1y4-8.91y2y3+ (27) (28) (29) 表3列出各设计参数的敏感性分析结果。 表3 侧撞工况的全局敏感性分析结果 由表3可知,侧撞工况下一体式框架是影响B柱侵入量的最主要因素,约占总影响的68%;前门加强筋横向布置于车门处,故侧撞过程中对侵入量影响较小,这与敏感性分析结果相符,另外前门加强筋对B柱中部最大侵入速度、非碰撞侧B柱下端加速度峰值影响较大;B柱内板和外板连接在一起,内板对外板起加固作用,其对各耐撞性指标的影响趋势较一致,敏感性分析结果也表明了这一点;各参数的相互作用对耐撞性指标影响较小,1阶和2阶敏感性指标之和近似等于1,故更高阶敏感性值非常小。 针对车身耐撞性问题,结合最优多项式选择技术提出了一种新型全局敏感性分析方法。该方法基于误差比例对多项式每一项的有效性进行评价,并构造了耐撞性指标和结构设计参数之间的最优多项式模型,这使采用直接积分法求解Sobol敏感性成为可能,有效提高了车身结构参数全局敏感性分析的效率和精度。基于该方法能准确地评价车身设计参数对耐撞性指标的敏感性,为车辆耐撞性设计和优化等提供了重要依据。 [1] CHOI K K, KIM N H. Structural Sensitivity Analysis and Optimization[M]. New York: Springer,2005. [2] SALTELLI A, CHAN K, SCOTT M. Sensitivity Analysis[M]. West Sussex: John Wiley & Son,2000. [3] HOLVOET K, VAN GRIENSVEN A, SEUNTJENS P, et al. Sensitivity analysis for hydrology and pesticide supply towards the river in SWAT[J]. Physics and Chemistry of the Earth,2005,30(8-10):518-526. [4] SALTELLI A, ANNONI P. How to Avoid a Perfunctory Sensitivity Analysis[J]. Environmental Modeling & Software,2010,25:1508-1517. [5] 张健,张鑫,李江,等.典型汽车碰撞模型自选参数的敏感性分析[J].汽车工程,2012,34(10):905-908. [6] CLOKE H L, PAPPENBERGER F, RENAUD J P. Multi-method Global Sensitivity Analysis (MMGSA) for Modeling Floodplain[J]. Hydrological Processes,2008,22(11):1660-1674. [7] TONG C. Self-validated Variance-based Methods for Sensitivity Analysis of Model Outputs[J]. Reliability Engineering & System Safety,2010,95(3):301-309. [8] SALTELLI A, RATTO M, ANDRES T, et al. Global Sensitivity Analysis: the Primer[M]. West Sussex: John Wiley & Sons,2008. [9] 陈涛,魏朗,龚标,等.车对车碰撞事故再现系统的参数敏感性分析[J].汽车工程,2012,34(9):771-776. [10] SOBLO I M. Sensitivity Estimates for Nonlinear Mathematical Models[J]. Mathematical Modeling and Computational Experiment,1993,1:407-414. [11] SOBLO I M, KUCHERENKO S. Derivative Based Global Sensitivity Measures and Their Link with Global Sensitivity Indices[J]. Mathematics and Computers in Simulation,2009,79:3009-3017. [12] SOBLO I M. Global Sensitivity Indices for Nonlinear Mathematical Models and Their Monte Carlo Estimates[J]. Mathematics and Computers in Simulation,2001,55:271-280. [13] YANG J. Convergence and Uncertainty Analysis in Monte Carlo Based Sensitivity Analysis[J]. Environmental Modeling & Software,2011,26(4):444-457. [14] KORENBERG M, BILLINGS S A, LIU Y P, et al. Orthogonal Parameter Estimation Algorithm for Non-linear Stochastic Systems[J]. International Journal of Control,1998,48:193-210. [15] XU D, LU F. Modeling Global Vector Fields of Chaotic Systems from Noisy Time Series with Aid of Structure-selection Techniques[J]. Chaos,2006,16:109-116. [16] HOU S J, DONG D, REN L L, et al. Multivariable Crashworthiness Optimization of Vehicle Body by Unreplicated Saturated Factorial Design[J]. Structural and Multidisciplinary Optimization,2012,46(6):891-905. [17] HOU S J, LIU T Y, DONG D, et al. Factor Screening and Multivariable Crashworthiness Optimization for Vehicle Side Impact by Factorial Design[J]. Structural and Multidisciplinary Optimization,2014,49(1):147-167. A Novel Sensitivity Analysis Method for Vehicle BodyCrashworthiness Based on Optimal Polynomial Models Liu Jie, Liu Guangzhao, Xu Can & Yu Zhongbo CollegeofMechanicalandVehicleEngineering,HunanUniversity,StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,Changsha410082 A novel global sensitivity analysis method based on optimal polynomial model is proposed to evaluate the sensitivity of structure parameters to vehicle body crashworthiness. The optimal polynomial models describing the relationship between crashworthiness indicators and structural design parameters are constructed with the structure selection technique for error reduction ratio, and the Sobol global sensitivity analysis is performed by direct integration. The method proposed overcomes the shortcomings of much computation efforts required and insecure results with traditional method. The results of sensitivity analysis for engineering examples of vehicle frontal and side crashes demonstrate the effectiveness and practicality of the method. vehicle body crashworthiness; global sensitivity; optimal polynomial; Sobol method *国家自然科学基金(11572115,11232004)和汽车车身先进设计制造国家重点实验室自主研究课题(51475003)资助。 原稿收到日期为2014年6月16日。2 基于结构选择的最优多项式模型
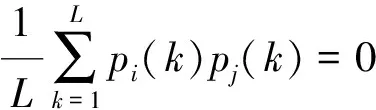

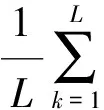
3 直接积分全局敏感性分析流程

4 数值算例

5 工程应用


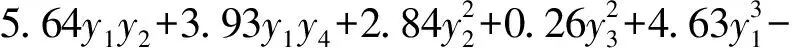

6 结论
