基于多学科设计优化的悬架互换研究

王 彧，闫瑞雷，黄向东

(广州汽车集团股份有限公司汽车工程研究院,广州 511434)

2016117

基于多学科设计优化的悬架互换研究

王 彧，闫瑞雷，黄向东

(广州汽车集团股份有限公司汽车工程研究院,广州 511434)

针对底盘平台前双叉臂悬架和麦弗逊悬架互换的问题，为兼顾具有耦合效应的静力学、运动学和动力学性能3个关键设计要素，根据多学科设计优化理论将其优化问题分解为一个系统级优化问题和3个关键设计要素优化问题，同时进行不同性能的并行设计，满足两种悬架结构在相同空间约束的前提下，实现各自性能目标。通过试验设计构建3个关键设计要素的Kriging模型，进行优化。结果表明，该方法较好地平衡了底盘静力学、运动学和动力学性能，具有较强的工程实用性。

多学科设计优化; 静力学; 运动学; 动力学; 悬架互换

前言

产品系列化、零部件通用化和产品设计标准化是现代汽车设计的基本要求。车型平台化结合系统集成与模块化技术，将车型平台分为车身、动力和底盘等模块，有利于降低设计和零部件成本，缩短开发周期。目前车身、动力等模块化技术比较成熟，而在底盘设计中更多的是同一悬架型式模块化，不同悬架型式可互换的底盘模块化技术尚不成熟。具体到底盘硬点设计优化方面，国内外很多学者都对底盘硬点进行了优化[1-4]，但只是针对K&C(kinematics & compliance)性能单一设计要素的优化，未能从底盘空间布置和零部件强度等学科综合考虑，只有将多学科的设计综合在一起进行协同优化，才能获得底盘的最佳性能。

多学科设计优化(multidisciplinary design optimization，MDO)是一种通过充分利用和探索系统中相互作用的协同机制来设计复杂系统和子系统的方法论，获得系统的整体最优解。国外大型汽车公司早已把多学科设计优化应用于车身结构设计[5-7]，而国内在汽车设计领域，如车身轻量化领域[8]，也开展了一些MDO研究，因此在汽车底盘设计领域开展MDO研究也非常必要。本文中对底盘的设计领域主要涵盖3个关键设计要素，分别是车辆动力学、运动学和静力学性能，建立了评价底盘性能的系统模型和涉及上述3个关键设计要素的数学模型，利用多学科协同优化方法对底盘硬点和零部件进行多学科优化，较好地解决了将双叉臂悬架换为麦弗逊悬架的底盘多学科设计问题。

1 底盘多学科设计优化

MDO研究的是复杂系统的设计优化问题，其通用的数学模型为

(1)

式中：f(x,y(x))为目标函数；hi(x,y(x))为等式约束；gj(x,y(x))为不等式约束，x为设计变量；y(x)为系统分析方程A(x,y(x))确定的状态方程。

系统分析方程A(x,y(x))为

(2)

式(2)即为多学科分析方程，其中N为MDO子系统的数目，各个子系统分析方程确定了学科分析和交叉耦合关系，状态方程y(x)一般以耦合差分方程描述。

针对本文中的研究对象，考虑到所要解决的是动力学、运动学和静力学交叉耦合关系，按多学科设计优化思路建立底盘多学科设计优化模型，如图1所示。底盘系统作为系统级优化目标，包含运动学、动力学和静力学性能3个关键设计要素，每个设计要素有各自的优化目标，例如动力学目标为K&C特性、静力学目标为质量和强度等，它们之间通过共享变量、耦合变量和局部变量进行信息传递，将复杂优化设计问题分解为各学科优化设计问题，并通过系统级约束条件来协调各学科之间的共享设计变量和耦合状态变量。每个子系统在子空间的设计变量子集与子空间分析得到的计算结果以最小方差方法进行优化。为提高计算效率，对3个关键设计要素建立了Kriging模型，使得在子学科优化中调用Kriging模型而不是仿真模型，从而减小计算量。

图1 底盘多学科协同优化流程图

2 底盘跨学科模型建立

在同一底盘平台上实现前悬架麦弗逊结构和双叉臂结构自由切换，可提升底盘平台车型的可拓展性和性能的多样化，提高底盘零部件沿用率，提高开发效率，降低开发成本，缩短底盘开发周期。

本文中所要解决的悬架互换工程问题为：(1)在底盘设计空间约束一致的情况下，两种悬架共用副车架、下摆臂和转向机及车身模块，将减振器上、下点，转向拉杆外点和下摆臂外点作为优化变量，转向节做适应性修改，如图2所示；(2)根据车型定位的不同，麦弗逊悬架和双叉臂悬架有不同的K&C特性范围，如前束、外倾、轮心纵向和侧向位移变化，两种悬架均存在差异，但需满足各自悬架的性能要求；(3)满足底盘零部件质量和成本要求，保证零部件强度和刚度。

图2 悬架互换示意图

2.1 动力学模型分析

悬架的K&C特性是底盘开发的关键环节，对整车的操纵稳定性和平顺性等具有重要的影响，研究悬架K&C特性的关键参数，可为底盘开发与调校工作提供理论依据。

本文中首先根据多体动力学理论，采用固联在构件上的连体坐标系来确定悬架系统的运动关系，如图3所示。连体坐标系o′x′y′z′的原点o′在全局坐标系oxyz下的坐标为T=[x,y,z]T， o′x′y′z′相对于全局坐标系oxyz的方位可用方向余弦矩阵表示。

图3 坐标变化示意图

用欧拉角表示的方向余弦矩阵为

C=

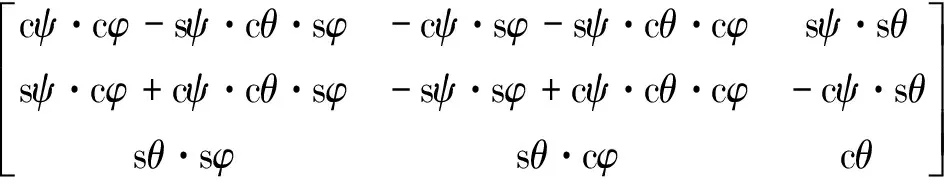
(3)

式中：c=cos；s=sin；ψ为进动角；θ为章动角；φ为自转角。

一般的坐标变换式为

rS=T+Cr′S

(4)

根据式(4)，建立麦弗逊悬架的运动约束方程，可求解得到轮心位移、前束及外倾的数学表达式为

(5)

式中：(xW,yW,zW)为轮心坐标；xW0和yW0为轮心初始位置的横、纵坐标；(xD,yD,zD)为轮心方向点；Δx和Δy分别为轮心纵向和侧向位移变化；toe和camber分别为车轮前束及外倾变化。

为描述悬架系统对车轮的约束作用，根据影响车轮姿态的主要因素，建立悬架K&C特性修正模型：

(6)

式中：d为轮心跳动量；矩阵[K]和[C]中的各元素分别为悬架K&C试验中的运动学及弹性运动学特性；Ftx，Fty和Mtz分别为轮胎接地点位置的纵向力、侧向力及回正力矩。

最后，根据各K&C参数对整车性能影响的灵敏度不同，对每一个K&C指标分配不同的权重系数，本文中动力学模型的优化目标为悬架K&C参数与其目标值的综合差异程度，其定义为

(7)

式中：Hi(i=1,2,3,4)分别为轮心纵向、侧向位移及前束、外倾特性；Hi0为悬架K&C特性目标值；ωi为各K&C指标的权重系数。

2.2 运动学模型分析

底盘数字样机(digital mock-up，DMU)分析是对产品的真实化计算模拟，主要用来模拟各种工况下底盘零部件的运动空间，从而分析在运动过程中，各个零部件之间的间隙是否满足设计要求，避免装车和车辆行驶时的干涉问题。

由于篇幅所限，本文中仅详细阐述下摆臂的运动学数学模型，其它零部件(如转向拉杆和车轮)类似。

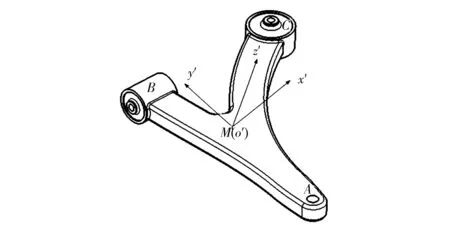
图4 下摆臂示意图

将“Y型臂”拆解成MA，MB和MC3段，在连体坐标系o′x′y′z′中分别建立数学模型：

(8)

式中：i=1,2,3分别表示“Y型臂”的MA，MB和MC3段；αi为各段与坐标轴的夹角。

根据式(4)，将“Y型臂”模型转化到惯性系下并进行简化，得

(9)

式中：A，B，C和M分别表示“Y型臂”的外点、前点、后点和中间点在全局坐标系下的坐标值。

图5和图6分别为转向拉杆和车轮的示意图。

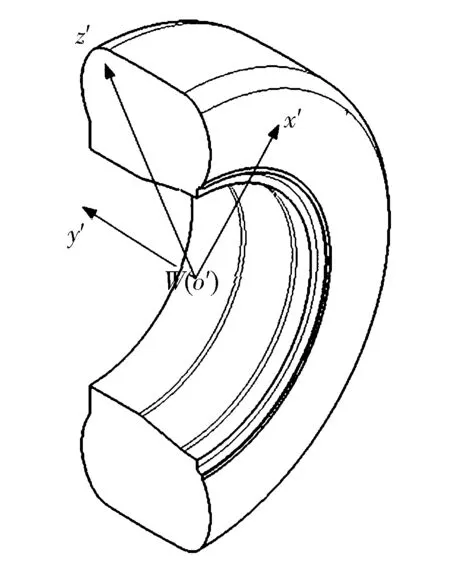
图6 车轮示意图

将转向拉杆模型转换到全局坐标系中并进行简化，得

frod=f(E,F,N,r)

(10)

式中：E，F和N分别表示转向拉杆外点、内点和质心位置在全局坐标系下的坐标值。

将车轮模型转化到全局坐标系中并进行相应简化，得

ftire=f(W,Ri,Ro,Rt)

(11)

式中：W表示轮心在全局坐标系下的坐标值；Ri，Ro和Rt分别为车轮内、外圈半径和胎冠半径。

综上所述，下摆臂、转向拉杆及轮胎之间的最小间隙可表示为

(12)

式中：i和j分别表示下摆臂、转向拉杆以及车轮中的任意两个零件。

2.3 静力学模型分析

本文中采用基结构方法对底盘零部件进行结构拓扑优化，以底盘轻量化为设计目标，以底盘基本拓扑结构的硬点和尺寸参数作为设计变量，约束条件为底盘的强度和刚度，下文以下摆臂为例进行拓扑优化。

2.3.1 载荷工况的确定

结构拓扑优化设计是建立在一定载荷工况约束条件的基础上，底盘拓扑优化的约束条件就是在各种典型载荷工况下的刚度和强度设计要求。典型载荷工况主要有：3.5g单轮冲击、0.7g倒车制动、1g制动、1g侧向加速度和撞击路肩5种工况，计算加载力如表1所示。

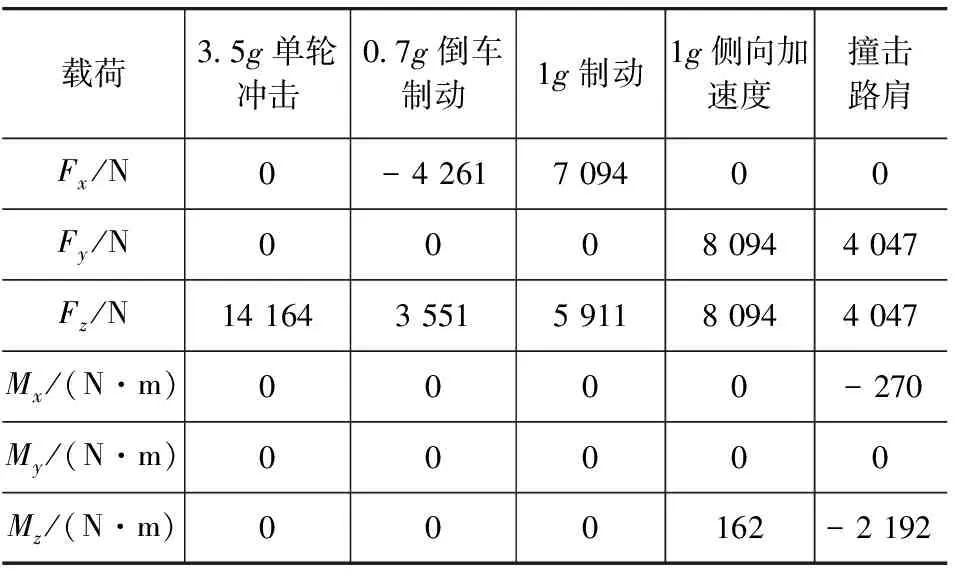
表1 下摆臂载荷工况

优化目标即为在上述5种工况载荷下，保证下摆臂的刚度和强度，使质量最小。

2.3.2 优化变量和约束条件

下摆臂优化设计变量为构件的截面尺寸与厚度，计算中材料为F45MnVS，密度为7 850kg/m3，弹性模量为210GPa，泊松比为0.3，屈服强度为550MPa。

底盘拓扑优化设计的目标是满足强度和刚度的前提下质量最小，其设计指标约束条件为：取第四强度理论，许用应力取屈服强度550MPa，安全系数为1.5，刚度要求最大挠度小于10mm，在此约束下实现底盘质量轻量化，其约束函数可表述为

(13)

式中：Umax(x)和σmax(x)为所有工况下底盘最大位移和最大正应力；[U]为许可挠度；[σ]为许用应力；n为安全系数。

3 优化模型的建立

3.1 优化问题表达

按照协同优化框架，将悬架系统的一体化设计问题分解为1个系统级优化问题和3个关键设计要素优化问题，分别是动力学、运动学和静力学性能。此外，从性能、装配及应力等方面对悬架系统进行系统级优化，优化目标为基于量纲为1的线性加权综合评价函数U最大化，U表示为

U=-λ1K+λ2G/G0-λ3m/m0

(14)

式中：λ1，λ2和λ3分别为加权性能指标函数K、加权间隙指标函数G和加权质量指标函数m的权重；下标0表示相应参数的初始值。

系统级优化模型为

(15)

式中：VU，VM和VL分别为共享变量、耦合变量和局部变量；角标“*”为各个学科系统级优化的最优值；ε为目标函数一致性约束松弛因子。

动力学优化问题描述为

(16)

式中：xi0，yi0，zi0表示各硬点的初始坐标值；V1为动力学子系统的局部变量且各硬点的约束空间为半径为r0的球体空间；P，Q表示减振器上、下点。

运动学优化问题描述为

(17)

式中：G0为零部件间的最小间隙值，此处规定G0=10mm；V2为运动学子系统的局部变量。

静力学优化问题描述如下。

设在底盘基础结构中有n个构件作为可设计域，其优化设计的数学模型为

(18)

式中：A=[A1,A2,…,An]T为摆臂和加强角片截面设计变量；n为底盘构件数；t=[t1,t2,…,tn]T为构件的拓扑设计变量，0表示构件不存在，1表示构件存在；J3为构件质量；ρi为构件密度；li为摆臂长度；ei为摆臂厚度；gi为约束函数，包括安装尺寸约束、强度刚度约束和动态特性约束等；Si为横截面设计变量的可取集；V3为静力学子系统的局部变量。

3.2 灵敏度与耦合强度分析

设计函数对设计变量的灵敏度可用函数的偏导数表示，因此，在某个设计点Xk处，设计函数φj(X)对设计变量xi的灵敏度可表示为

(j=1,2,…,m;i=1,2,…,n)

(19)

式中：m和n分别为设计函数和设计变量的个数。根据式(19)，计算各变量之间耦合因素的灵敏度，计算结果如表2所示。

表2 共享变量灵敏度计算结果

为减轻各学科之间的耦合程度，提高解耦效率，结合设计函数灵敏度值|Sji|的大小，通过建立隶属度函数，对共享变量的耦合强度进行判定：

μA(|Sji|)=

(20)

其中：

式中：max|Sji|和min|Sji|分别表示同一学科内最大与最小灵敏度值。

根据式(20)计算|Sji|的隶属度，计算结果如表3所示。

表3 耦合因素的隶属度

根据表3和强弱耦合因素的判断准则可知，zA为系统级强耦合因素，xA，yA，h和e为运动学和静力学的强耦合因素，因此，需要进行两次协同优化，获得底盘系统整体最优解。

3.3 近似模型

目前，Kriging模型已经成为MDO中比较有代表性的一种代理模型近似方法。底盘设计优化过程是一个高度非线性的动态过程，Kriging方法适用性强，对线性模型和非线性模型近似时都有比较明显的优势[9]。它由全局模型和局部偏差迭加而成，表示为

y(x)=f(x)+Z(x)

(21)

式中：y(x)为未知的Kriging模型；f(x)为已知的关于x的函数，一般用常数β代替；Z(x)为均值为零、方差为σ2、协方差不为零的随机过程。

未知x处响应值y(x)预测近似模型表达式为

y(x)=β+rT(x)R-1(y-fβ)

(22)

式中：R为样本的相关矩阵；y为样本数据的响应值；f为全1列向量；r(x)为样本点和预测点所组成的相关变量。

其中：

rT(x)=[R(x,x1),R(x,x2),…，R(x,xn)]T

β=(fTR-1f)-1fTR-1y

采样点xi,xj的相关函数为

(23)

式中：θk为未知相关参数向量；n为采样点个数。

全局模型的方差估计值为

(24)

式中ns为采样点数。

通过极大似然估计确定参数θk，即可求解非线性无约束最优化问题：

(25)

当θk求出后，就可得到未知点x和已知样本数据之间的相关矢量rT(x)，通过式(25)得到其响应值，完成Kriging近似模型的构建。

考虑到底盘多学科仿真计算时间相对较长，在底盘优化中，调用的是Kriging模型而不是仿真模型，图7为构造K&C性能目标得到的Kriging模型在试验样本点的相对误差。

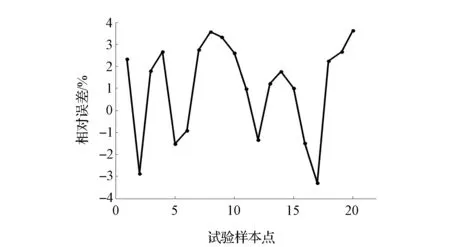
图7 K&C性能近似模型的相对误差

4 优化结果验证

本节将各关键设计要素综合在一起，采用NSGA-II算法对系统级和子系统级模型进行协同优化[10]，获得满足底盘设计要求的硬点和底盘零件的结构参数，并对优化结果进行K&C试验验证，如表4、图8和图9所示，图8中试验值即为优化后结果。

表4 优化结果

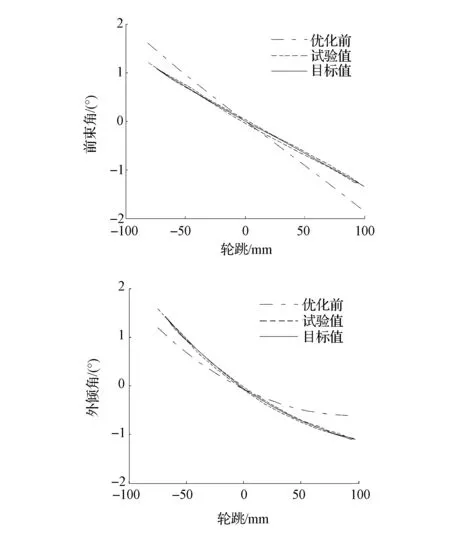
图8 K&C性能对比图

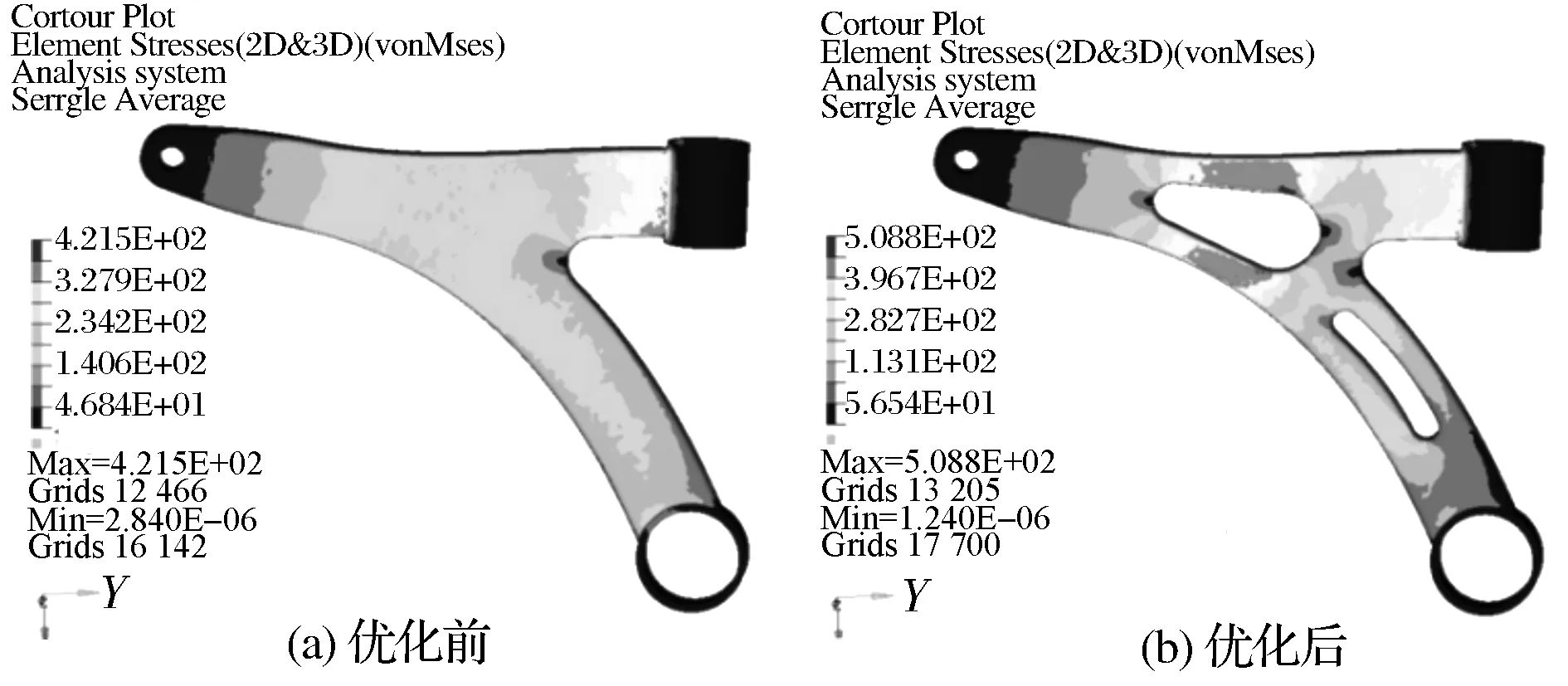
图9 下摆臂应力示意图

从优化结果来看，悬架K&C特性得到明显改善且与设计目标吻合较好；各零部件间的间隙得到改善，降低了布置风险；在满足强度要求的前提下，底盘下摆臂质量减小了0.77kg，达到底盘整体性能最优。

5 结论

(1)悬架互换技术是底盘模块化的一部分，能够有效提高底盘零部件的通用率，降低底盘研发成本，提高研发效率。

(2)将多学科协同优化方法与Kriging模型技术应用到悬架互换设计中，避免了传统底盘开发过程的串行设计，实现了3个关键设计要素的并行设计，大大提高了研发效率。

(3)对悬架硬点及底盘零部件的结构优化实例研究表明，该方法具有较强的工程实用性，能够有效提高悬架系统的整体性能。

[1] TOTU Vlad, ALEXANDRU Catalin. Multi-criteria kinematic opti-

mization of a front multi-link suspension mechanism using DOE screening and regression model[J]. Applied Mechanics and Materials,2013,332:351-356.

[2] MANTARAS D A,LUQUE P,VERA C. Development and validation of a three-dimensional kinematic model for the McPherson steering and suspension mechanisms[J]. Mechanism and Machine Theory,2004,39(6):603-619.

[3] 丁飞，韩旭，刘桂萍，等.悬架导向机构硬点灵敏度分析及多目标优化设计[J].汽车工程，2010，32(2)：137-142.

[4] 奉铜明，钟志华，闫晓磊，等.基于NSGA-II算法的多连杆悬架多目标优化[J].汽车工程，2010,32(12)：1063-1066.

[5] SOBIESZCZANSI-SOBIESKI J,KODIYALAM S,YANG R Y. Optimization of car body under constraints of noise, vibration，and harshness(NVH), and crash[J]. Structural and Multidisciplinary Optimization,2001,22(4):295-306.

[6] CRAIG K J, NIELEN S, DOOGE D A, et al. MDO of automotive vehicle for crashworthiness and NVH using response surface methods[C]. The 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization,Atlanta，Georgia，2002：1-12.

[7] ADI A H，PANAH M S.Multi-objective optimal design of a passenger car’s body[C].ASME 10th Biennial Conference on Engineering Systems Design and Analysis，Istanbul,2010.

[8] 张勇，李光耀,孙光永，等.多学科设计优化在整车轻量化设计中的应用研究[J].中国机械工程,2008,19(7)：877-881.

[9] SIMPSON T W,MAUERY T M, KORTE, J J, et al.Comparison of response surface and kriging models for multidisciplinary design optimization[J].7th Symposium on Multidisciplinary Analysis Optimization,St.Louis,MO,AIAA-98-4755.

[10] CHEN S, SHI T,WANG D,et al. Multi-objective optimization of the vehicle ride comfort based on Kriging approximate model and NSGA-II[J]. Journal of Mechanical Science and Technology, 2015,29 (3) :1007-1018.

A Research on Suspension Exchange Based on Multidisciplinary Design Optimization

Wang Yu,Yan Ruilei & Huang Xiangdong

GACEngineering，Guangzhou511434

Aiming at the problem of exchange between front double wishbone suspension and Macpherson suspension, for concurrently considering three key design factors, i.e. statics, kinematics and dynamics performances having coupling effects each other, their optimization problems are divided into a system level optimization problem and three key design factor optimization problems based on multidisciplinary design optimization (MDO) theory. With parallel designs proceeded concurrently, on the premise of meeting the same spatial constraints for both suspension structures, each realizes its own performance objective. The Kriging models for three key design factors are constructed by the design of experiment with optimizations performed. The results show that the method proposed achieves better balance among chassis performances of statics, kinematics and dynamics with strong engineering practicality.

multidisciplinary design optimization; statics; kinematics; dynamics; suspension exchange

原稿收到日期为2015年5月25日，修改稿收到日期为2015年8月5日。