动力总成液压悬置系统固有属性的拉普拉斯域分析方法*

2016-04-17陈潇凯

汽车工程 2016年6期

关键词：幅值流体坐标系

宋康, 陈潇凯, 林逸

(1.北京理工大学机械与车辆学院,北京 100081； 2.北京汽车股份有限公司汽车工程研究院,北京 101300)

2016116

动力总成液压悬置系统固有属性的拉普拉斯域分析方法*

宋康1, 陈潇凯1, 林逸2

(1.北京理工大学机械与车辆学院,北京 100081； 2.北京汽车股份有限公司汽车工程研究院,北京 101300)

针对液压悬置随激振频率呈非线性变化的动刚度特性，采用了一种拉普拉斯域分析方法计算动力总成液压悬置系统的固有属性。首先，建立液压悬置的集中参数线性流体模型，分析悬置在低频段和高频段的稳态动刚度特性，而得到悬置的宽频动刚度表达式。接着建立悬置系统在曲轴坐标系下的振动模型，在拉普拉斯域内直接应用液压悬置的动刚度表达式推导系统固有属性的分析方法。最后采用这一新方法计算了某液压悬置系统的固有属性。结果显示，液压悬置系统具有复特征值和复模态向量。复特征值同时包含系统的固有频率和阻尼比信息；根据阻尼比、复模态向量的幅值等信息可对模态类型作出判断；结合复模态向量的相位信息可确定模态的具体形状。

动力总成悬置系统；液压悬置；动刚度；固有属性；拉普拉斯域

前言

在动力总成悬置系统的设计中，理想的悬置元件应该具有低频大刚度、大阻尼，高频小刚度、小阻尼的特性。与弹性体悬置相比，液压悬置所具有的动刚度特性更加符合该设计要求，因此，液压悬置在悬置系统的设计中得到了越来越广泛的应用。

鉴于液压悬置在特性上的优势，国内外对液压悬置开展了广泛研究，包括对悬置建模、性能分析和对采用液压悬置的机械系统性能的研究等。文献[1]中提出了线性时不变集中参数流体-机械模型，该模型在低频段与试验数据拟合良好，前人提出的多数模型均可看作该模型在特定条件下的简化版本。文献[2]中提出了基于有限测量数据对液压悬置的性能参数进行预测的方法，分别给出了悬置在低频段和高频段的等效机械模型，并在此基础上提出了液压悬置的宽频模型。文献[3]中建立了惯性通道-解耦盘式液压悬置的力学模型和数学模型，分析了模型各参数对悬置动特性的影响。文献[4]和文献[5]中建立了液压悬置的线性和非线性集中参数模型并提出了模型参数的识别方法。虽然集中参数模型已能对液压悬置的频变刚度特性进行较为精确的预测，但由于该模型具有不同的驱动点刚度和被动点刚度，因此在机械系统的建模中须要对二者加以区别[2,6-7]。文献[8]中将液压悬置动刚度的测量值引入车辆或通用机械系统的建模，并根据系统阻尼的不同处理方式总结了特征值问题的多种计算方法。文献[9]和文献[10]中在动力总成悬置系统的设计中考虑了液压悬置内部流体的惯性，增加了振动系统的自由度，建立了扩展系统的时域运动方程，扩展后的模型能同时对动力总成和液压悬置的固有属性进行预测。对于动力总成液压悬置系统，时域方法虽然能够对系统属性进行全面预测，但运动方程的建立过程较为繁琐，并且扩展模型的物理意义不明确；尤其是当扩展系统的维数较大时，计算效率和精度均会下降。

本文中首先建立了液压悬置的集中参数流体模型，得到悬置动刚度的解析表达式；然后建立了动力总成悬置系统的振动模型，推导得出了系统在拉普拉斯域内的固有属性分析方法；最后以某液压悬置系统为例，采用新方法计算得到系统的固有属性。

1 液压悬置的集中参数线性模型

以惯性通道-解耦盘式液压悬置为例，该类型悬置可以简化为如图1所示的集中参数流体模型。液压悬置内部分为2个液室：上液室和下液室。上液室的压强为p1，体积柔度为C1；下液室的压强为p2，体积柔度为C2。上、下液室之间通过惯性通道和解耦盘通道相连通。惯性通道的液体惯量为Ii，阻力为Ri，流量为qi；解耦盘通道的液体惯量为Id，阻力为Rd，流量为qd。橡胶主簧的刚度为kr，阻尼为cr，液室的有效作用面积为A。

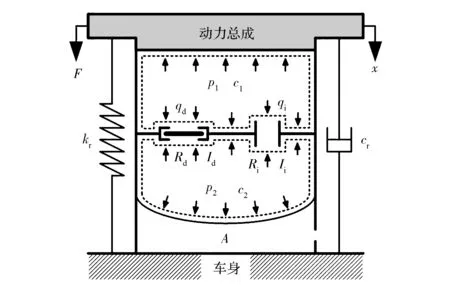
图1 液压悬置集中参数流体模型

液压悬置内部流体的动力学方程为

(1)

式中：前2个方程为流体的动量方程；后2个方程为流体的连续性方程。

已知液压悬置的上端与动力总成相连，下端与车身相连。假设悬置上端的位移为x，悬置受到的作用力为F，则F为

(2)

现定义如下：mi=A2Ii，ci=A2Ri，md=A2Id，cd=A2Rd，dxi/dt=qi/A，dxd/dt=qd/A，k1=A2/C1，k2=A2/C2。根据各变量的定义，式(1)与式(2)可改写为

(3)

方程的改写表示，由式(1)和式(2)表征的液压悬置流体模型被转化为由式(3)表征的机械模型。该等效机械模型在作用效果上与原流体模型相同。

当激励频率较低而幅值较大时，解耦盘基本保持关闭状态，液体主要通过惯性通道进行流动，此时悬置所表现出的性能与惯性通道式液压悬置相似，悬置动刚度与流体通过惯性通道的能量损失密切相关。当激励频率接近惯性通道内液体的固有频率时，悬置动刚度将达到最大。悬置在低频段(qd= 0)的动力学方程为

(4)

当激励频率较高而幅值较小时，惯性通道内的液体几乎不再流动，此时液体主要通过解耦盘进行流动。悬置在高频段(qi= 0)的动力学方程为

(5)

假定系统具有零初始条件(如不作特殊说明，下文在作拉普拉斯变换时均假定初始条件为0)并考虑到k1远大于k2，对式(4)和式(5)进行拉普拉斯变换得到悬置的动刚度表达式为

(6)

对于式(6)，在低频段内，m0=mi，c0=ci；在高频段内，m0=md，c0=cd。式(6)对应液压悬置的宽频模型，研究结果表明，该模型的有效频率范围可达300Hz[2]。

需要说明，上述给出的液压悬置集中参数流体模型或等效机械模型属于稳态模型，该模型只能针对低频激励或高频激励作稳态分析，但无法对频率的过渡段给出可信的结果，这是由于该频段涉及解耦盘工作状态的选择机制。另外，建模过程中还忽略了诸如真空效应、湍流等典型的非线性效应[11]。

2 动力总成悬置系统的固有属性分析方法

对于采用弹性体悬置的动力总成悬置系统，在小阻尼条件下，系统的固有属性可根据质量(惯量)特性和刚度特性进行确定，计算得到的特征值为实数，特征向量为实向量。如果考虑阻尼对系统振动特性的影响，则确定系统的固有属性时还要用到阻尼特性，此时计算得到的特征值一般为复数，特征向量为复向量。

对于弹性体悬置，动刚度和滞后角基本随频率呈线性变化，这就说明悬置的刚度kr和阻尼cr基本可以是频率恒定的。弹性体悬置动刚度的表达式为

(7)

对于液压悬置，随着激励频率的增加，悬置的动刚度和滞后角均呈现出典型的非线性变化关系，因此，对于采用液压悬置的动力总成悬置系统，其固有属性的分析将更加复杂。针对该问题，本节提出了悬置系统在拉普拉斯域内的固有属性分析方法。

2.1 系统建模

在对动力总成悬置系统建模时，将动力总成简化为刚体；弹性体悬置与液压悬置均简化为3个相互正交的弹簧，各弹簧刚度以动刚度的形式给出。动力总成悬置系统的振动模型如图2所示。

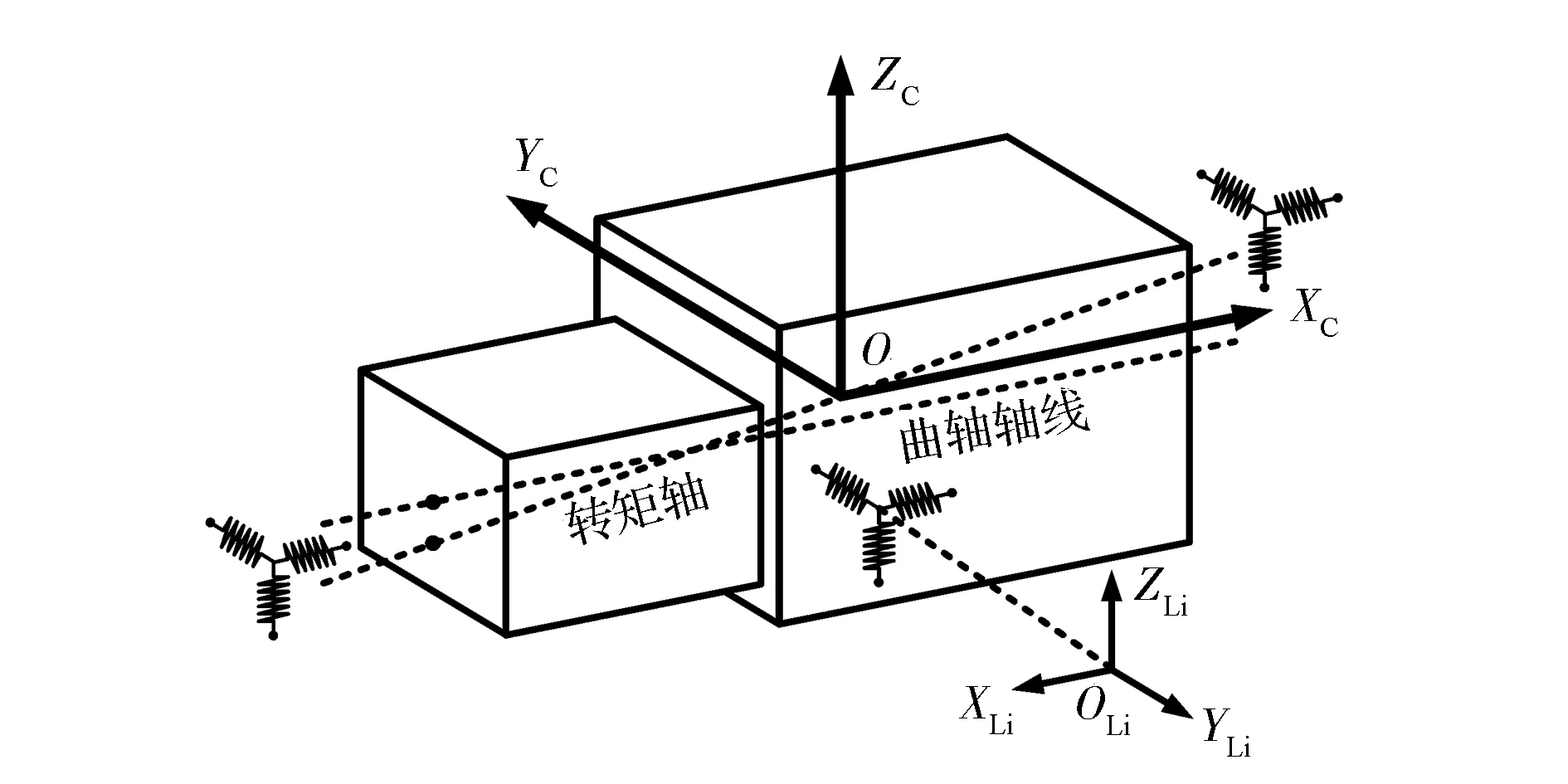
图2 动力总成悬置系统的振动模型

以曲轴坐标系{XC，YC，ZC}作为建立系统运动方程和计算固有属性的参考坐标系。曲轴坐标系的原点位于动力总成质心处，XC轴沿曲轴轴线指向汽车前方，ZC轴沿直列气缸轴线或V型气缸角平分线指向上方，YC轴根据右手定则确定。同时，在每个悬置处建立局部坐标系，第i个悬置处的局部坐标系定义为{XLi，YLi，ZLi}，悬置的动刚度在局部坐标系中表示。

2.2 拉普拉斯域内的固有属性分析方法

在拉普拉斯域内，液压悬置在流体起作用方向(通常定义为垂向)的动刚度与频率呈典型的非线性关系，而在另外两个方向的动刚度则近似认为与弹性体悬置相同。在局部坐标系内，悬置的动刚度可表示为

(8)

重新观察式(8)，对于液压悬置的垂向动刚度表达式，如果将公式中的参数m0与c0设置为0，则该式在形式上就与弹性体悬置的动刚度表达式相同。因此，通过对液压悬置刚度矩阵中的参数作不同设置，可以得到弹性体悬置与液压悬置刚度矩阵的通用表达式。根据液压悬置的物理结构，将参数m0与c0设置为0是忽略悬置内部流体的作用，这种情况相当于去除液压悬置的液压油，只有橡胶主簧发挥作用。

根据旋量理论，第i个悬置局部坐标系原点的位移dLi与动力总成质心的位移d满足如下关系式：

(9)

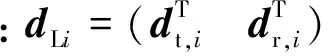
式中：RC,Li为由第i个局部坐标系至曲轴坐标系的旋转矩阵；ri为第i个局部坐标系在曲轴坐标系中的位置向量；ad(ri)为向量ri的伴随变换形式。

对式(9)等号左右两侧同时进行拉普拉斯变换L可得

(10)

根据第i个悬置在局部坐标系中的位移dLi及由此产生的反作用力FLi计算得到悬置动刚度KLi(s)的表达式为

(11)

其中动刚度KLi(s)表示为

根据旋量理论，作用在动力总成质心且与悬置作用力FLi等效的作用力Fi表示为

Fi=AdgC,LiFLi

(12)

对所有力旋量Fi进行求和计算，所得结果即为动力总成质心的位移向量d引起的作用力旋量F：

(13)

对式(13)等号左右两侧同时进行拉普拉斯变换可得

(14)

将式(10)～式(12)代入式(14)可得

(15)

根据式(15)可得系统动刚度矩阵K(s)的表达式为

(16)

动力总成悬置系统的运动方程可写为

(17)

式中：M为系统的广义质量矩阵；FE为系统受到的外部激励。

对式(17)等号左右两侧同时进行拉普拉斯变换并代入式(15)和式(16)可得

s2ML[d]+K(s)L[d]=L[FE]

(18)

令

Z(s)=s2M+K(s)

系统传递函数T(s)的表达式为

(19)

式中adj[Z(s)]表示Z(s)的伴随矩阵。

根据振动模态理论，式(19)的分母，即Z(s)的行列式，称为系统的特征方程。特征方程的根，即为系统的特征值，每个特征值都同时包含系统的固有频率与模态阻尼比信息[12]。

对于系统的第r个特征值λr，记与之相应的特征向量为ur。特征值λr与特征向量ur满足如下方程：

(20)

根据式(20)计算得到的特征向量只含有6个元素，对应动力总成的6个自由度。对于液压悬置的等效机械模型，当系统发生固有振动时，流体集中质量元素也具有相应的位移xM,i(xi或xd)。对于系统的第r阶固有振动，根据式(6)计算得到位移xM,i：

(21)

式中：uLi,r为第i个悬置在系统发生第r阶固有振动时的位移向量，该向量在局部坐标系中表示，可参照式(10)坐标系转换方法进行计算；uLi,r(3)为向量的第3个元素。

对于采用了N个液压悬置的动力总成悬置系统，完整的系统特征向量Ur可写为

(22)

至此，根据式(19)和式(22)可分别计算得出系统的全部特征值和完整的特征向量。由于系统的传递函数在拉普拉斯域中表示，因此推导过程中可直接采用式(6)给出的液压悬置动刚度表达式。与时域方法相比，传递函数矩阵仍然为6维矩阵，但是却可以一次性计算得到6+N个特征值和相应的特征向量，无须对振动系统的自由度进行扩展。而且，式(21)具有明确的物理意义，反映了当系统发生固有振动时，流体集中质量元素的位移与动力总成位移之间的传递关系。

3 应用算例

以某2.3L直列四缸四冲程动力总成的悬置系统为例，说明拉普拉斯域分析方法在系统固有属性计算中的应用。已知动力总成的质量为216kg，惯量参数在曲轴坐标系中测量，结果如表1所示。

表1 动力总成惯量参数 kg·m2

系统共采用3处悬置，分别为安装于变速器一侧的左悬置、安装于发动机一侧的右悬置和安装于发动机后方的后悬置。其中，左悬置与后悬置为弹性体悬置，右悬置为惯性通道式液压悬置。系统中各悬置的安装位置、安装方向和弹性体悬置的刚度值分别如表2～表4所示。悬置的安装位置在曲轴坐标系中描述；安装方向以局部坐标系与曲轴坐标系各坐标轴之间的夹角表示；悬置的刚度和阻尼在局部坐标系中描述。

表2 悬置安装位置 mm

表3 悬置安装方向 (°)

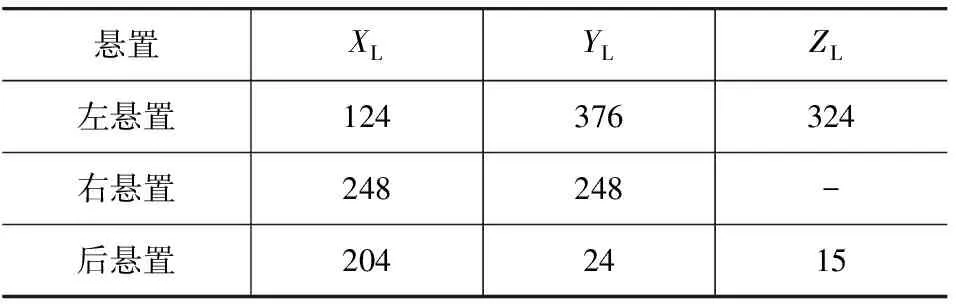
表4 悬置刚度 N·mm-1

液压悬置的结构参数为：橡胶主簧刚度kr= 168N/mm，主簧阻尼cr= 100N·s/m，流体等效集中质量mi= 50.3kg，等效刚度ki= 250N/mm，等效阻尼ci= 2582N·s/m。另外，所有弹性体悬置的阻尼均设置为100N·s/m。

根据第2节给出的动力总成液压悬置系统在拉普拉斯域内的固有属性分析方法，计算系统的特征值与特征向量(模态向量)。对计算得到的特征值作进一步处理而得到系统的固有频率和模态阻尼比，结果如表5所示；由于模态向量以各元素(复数)比值的形式给出，因此设定向量中第1个元素(对应动力总成的侧向平动自由度)的幅值为1，相位角为0，参考该设定计算得出向量中的其他各元素。系统复模态向量的幅值和相位信息分别如表6和表7所示。在表6中，Tx，Ty和Tz分别表示模态向量幅值在XC轴，YC轴和ZC轴平动自由度上的分量；Rx，Ry和Rz分别表示向量幅值在相应各轴转动自由度上的分量；Tm表示向量幅值在流体等效集中质量平动自由度上的分量。

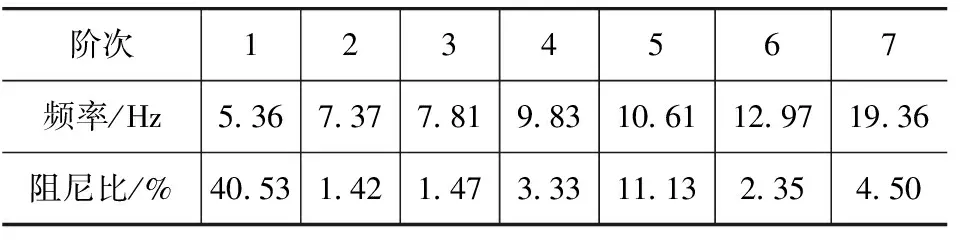
表5 系统各阶固有频率与阻尼比

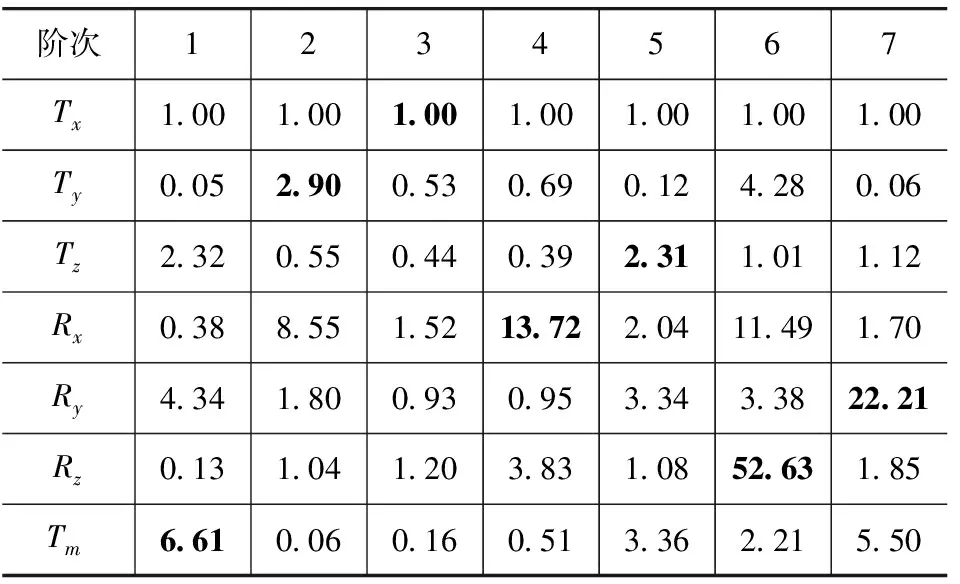
表6 系统复模态向量的幅值

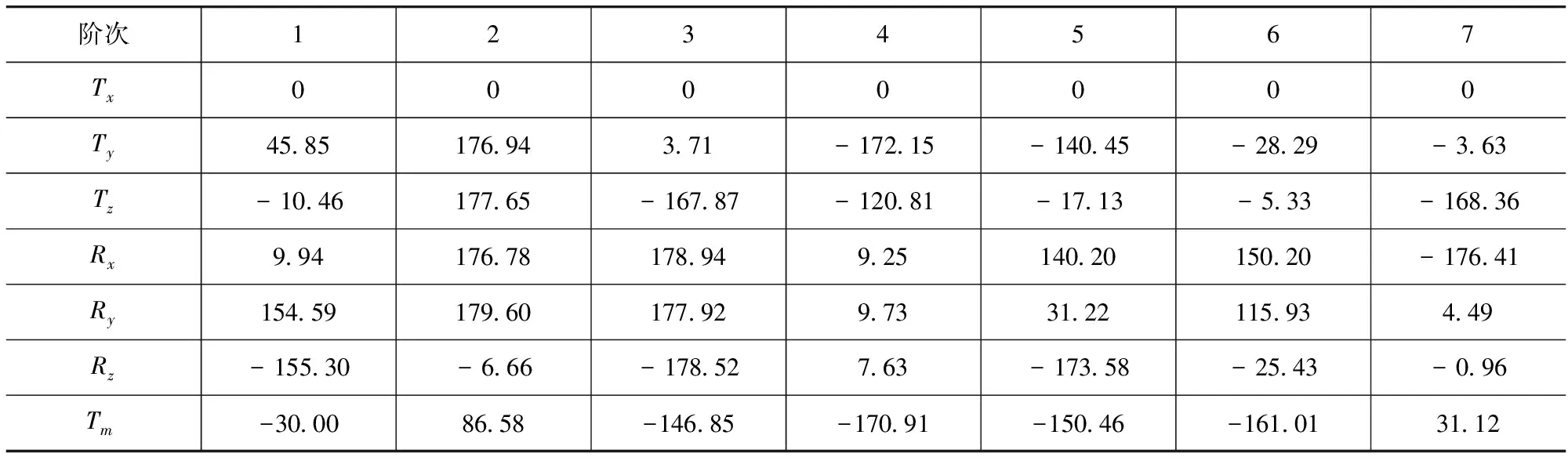
表7 系统复模态向量的相位 (°)

该动力总成悬置系统具有7阶固有频率。其中，6阶固有频率对应动力总成刚体的共振频率，1阶固有频率对应液压悬置惯性通道内流体的共振频率。

根据表5中的结果可知，第1阶模态的阻尼比为40.53%，远大于其他各阶模态的阻尼比；同时，根据表6中的结果可知，在第1阶模态向量中，流体等效集中质量的相对幅值Tm为6.61，是向量中的最大分量。因此，根据上述分析可以判定，系统的第1阶固有频率对应液压悬置惯性通道内流体的共振频率；由于悬置内部的等效阻尼非常大，因此系统的阻尼比处于相对较高的水平。

根据表6中的幅值信息可知，系统的第4阶、第6阶和第7阶模态向量中均存在幅值占比较大的元素，因此判定这3阶模态分别对应系统的俯仰模态、横摆模态和侧倾模态。其中，系统的第4阶模态尤为重要，这是因为该阶模态与系统在转矩作用下的隔振性能设计密切相关。

对于系统的第2阶、第3阶和第5阶模态，无法根据幅值信息对模态类型作出直观判断。例如，对于第2阶模态向量，虽然最大元素对应Rx方向，但与第4阶模态相比，Rx元素在模态向量中所占的比重显然要小一些；对于第3阶和第5阶模态，模态向量中存在多个幅值相差不大的元素，因此不易作出直观判断。

为了对模态的类型进行判定，现提出2条参考标准：第1条标准是模态能量百分比。由于动力总成的质量与惯量在大小上基本相差一个数量级，因此，模态向量中的平动分量对模态能量百分比的影响更大。参考这一标准，判定第2阶模态对应系统的纵向平动模态，第3阶模态对应系统的侧向平动模态，第5阶模态对应系统的垂向跳动模态。

第2条标准是液压悬置集中流体质量的运动与动力总成各向运动之间的耦合程度。由于液压悬置安装于动力总成右侧，因此，集中流体质量的运动将与动力总成的垂向跳动和侧倾转动产生较强的耦合，这一点可以根据第1阶模态向量和第7阶模态向量进行验证。前述分析已经判定第1阶频率对应液压悬置惯性通道内流体的共振频率，根据表6中的信息可知，第1阶模态向量中除了最大的Tm分量外，Tz分量和Ry分量的幅值也较大；对于第7阶模态，已经判定该阶模态对应系统的侧倾模态，模态向量中除了最大的Ry分量，Tm分量的幅值也较大。第1阶模态和第7阶模态的分析结果符合第2条标准。因此，对于系统的垂向跳动模态，模态向量中的Tz分量和Tm分量一定同时具有较大的幅值，据此判定第5阶模态对应系统的垂向跳动模态。

根据表6中的幅值信息虽然可以对模态的类型作出判断，但是还需要根据表7中的相位信息确定模态的具体形状。相位信息对系统第1阶、第5阶和第7阶模态形状的判断尤为重要。对于集中流体质量的运动和动力总成的垂向跳动，虽然由第1阶和第5阶模态向量中的幅值信息可以看出二者的耦合效应非常明显，但根据表7中的相位信息可知，二者在第1阶模态中的相位差为15.54°，而在第5阶模态中的相位差为133.33°，因此，二者在系统发生第1阶固有振动时倾向于同相运动，而在第5阶固有振动时倾向于反相运动。同样，对于集中流体质量的运动和动力总成的侧倾转动，二者在第1阶固有振动时倾向于反相运动，而在第7阶固有振动时倾向于同相运动。

4 结论

(1)液压悬置的集中参数流体模型或等效机械模型可较为准确地反映悬置的频变动刚度特性，能够同时用于悬置在低频段与高频段的稳态性能分析；但由于该模型为稳态模型，因此无法模拟悬置的解耦盘选择机制等非线性行为。

(2)拉普拉斯域分析方法可直接将液压悬置的动刚度表达式用于系统传递函数的推导；在不增加系统自由度的前提下，该方法可以一次性计算出系统的全部特征值；推导过程同时涉及系统的总体刚度特性和液压悬置的结构特性，因而物理意义明确。

(3)动力总成液压悬置系统具有复特征值及复模态向量。复特征值同时包含系统的固有频率及阻尼比信息；根据阻尼比、复模态向量的幅值等信息可以对模态类型作出判断；结合复模态向量的相位信息可以确定模态的具体形状。

[1]SINGHR,KIMG，RAVINDRAPV.Linearanalysisofautomotivehydro-mechanicalmountwithemphasisondecouplercharacteristics[J].JournalofSoundandVibration, 1992, 158(2): 219-243.

[2]HES,SINGHR.Estimationofamplitudeandfrequencydependentparametersofhydraulicenginemountgivenlimiteddynamicstiffnessmeasurements[J].NoiseControlEngineeringJournal, 2005, 53(6): 271-285.

[3] 冯振东，王立公，宋传学．动力总成液力悬置的动特性仿真[J]．汽车工程，1994，16(4)：193-198.

[4] 吕振华，梁伟，上官文斌．汽车发动机液阻悬置动特性仿真与实验分析[J]．汽车工程，2002，24(2)：105-111.

[5] 上官文斌，吕振华．液阻型橡胶隔振器非线性特性仿真分析[J]．振动工程学报，2003，16(4)：393-398.

[6]LEEJH,BAEMS,KIMKJ.Limitationsofmechanicalmodelwithlumpedmassinrepresentingdynamiccharacteristicsofhydraulicmount[C].SAEPaper2003-01-1466.

[7]LEEJH,SINGHR.Criticalanalysisofanalogousmechanicalmodelsusedtodescribehydraulicenginemounts[J].JournalofSoundandVibration, 2008, 311(3-5): 1457-1464.

[8]JEONGT,SINGHR.Inclusionofmeasuredfrequencyandamplitude-dependentmountpropertiesinvehicleormachinerymodels[J].JournalofSoundandVibration, 2001, 245(3): 385-415.

[9]PARKJY,SINGHR.Roleofspectrallyvaryingmountpropertiesininfluencingcouplingbetweenpowertrainmotionsundertorqueexcitation[J].JournalofSoundandVibration, 2010, 329(14): 2895-2914.

[10]HUJF,CHENWW,HUANGH.Decouplinganalysisforapowertrainmountingsystemwithacombinationofhydraulicmounts[J].ChineseJournalofMechanicalEngineering, 2013, 26(4): 737-745.

[11]ADIGUNAH,TIWARIM,SINGHR,etal.Transientresponseofahydraulicenginemount[J].NoiseControlEngineeringJournal, 2003, 268(2): 217-248.

[12] 沃德·海伦，斯蒂芬·拉门兹，波尔·萨斯．模态分析理论与试验[M]．北京：北京理工大学出版社，2001：3-26.

Analysis Method of Natural Properties of Powertrain Hydraulic Mounting System in Laplace Domain

Song Kang1, Chen Xiaokai1& Lin Yi2

1.SchoolofMechanicalEngineering,BeijingInstituteofTechnology,Beijing100081; 2.BeijingAutomotiveTechnologyCenter,BAICMotorCorporationLtd.,Beijing101300

In view of that the dynamic stiffness of hydraulic mount nonlinearly changes with excitation frequency, a Laplace domain analysis method is adopted to calculate the natural properties of powertrain hydraulic mounting system. Firstly a linear fluid model with lumped parameters for hydraulic mount is built, the steady state dynamic stiffness characteristics of powertrain mount in both low and high frequency bands are analyzed, and the dynamic stiffness expression for powertrain mount in a wide frequency range is obtained. Then a vibration model for powertrain mount is created in crankshaft coordinates and an analysis method of the natural properties of system is derived by directly applying dynamic stiffness expression of hydraulic mount in Laplace domain. Finally this new method is used to calculate the natural properties of a hydraulic mounting system. The results indicate that hydraulic mounting system has complex eigenvalues and complex modal vectors, in which eigenvalues contain information of the natural frequency and damping ratio of system. The type of mode can be judged according to damping ratio and the magnitude of complex modal vector, while the specific mode shapes can be determined based on phase information of complex modal vectors.

powertrain mounting system; hydraulic mount; dynamic stiffness; natural properties; Laplace domain

*国家自然科学基金(51275040)资助。

原稿收到日期为2014年12月25日。