基于小信号模型的新型Buck变换器补偿网络设计*

夏兴国， 陈乐柱， 潘小波， 张庆丰

(1.马鞍山职业技术学院 电气工程系, 安徽 马鞍山 243031；2.安徽工业大学 电气与信息工程学院, 安徽 马鞍山 243002)



基于小信号模型的新型Buck变换器补偿网络设计*

夏兴国1， 陈乐柱2， 潘小波1， 张庆丰1

(1.马鞍山职业技术学院 电气工程系, 安徽 马鞍山 243031；2.安徽工业大学 电气与信息工程学院, 安徽 马鞍山 243002)

摘要：对Buck变换器主电路在CCM工作模式下进行动态小信号分析，详细推导其状态方程得出小信号模型.先后设计3种闭环控制补偿网络，即PD，PID和双极点-双零点补偿网络，推导出补偿网络后系统的开环传递函数，由Matlab仿真出补偿网络补偿前后的开环传递函数的伯德图.结果表明，双极点-双零点补偿网络设计后，相角裕度为51.1°，稳态误差为0，在高频段幅频特性的下降频率为-40 dB/dec，获得了更好的稳态和动态性能，能更好地抑制高频干扰，这对研究其他开关电源有着非常好的借鉴作用.

关键词：Buck变换器；补偿网络；CCM模式；小信号模型；双极点-双零点

在Buck变换器的设计中，反馈补偿控制电路尤为重要，关系到整个电路及系统的稳定性、响应速度、过冲等性能指标.建模是研究和分析其稳定性和瞬态响应的基础，对变换器的分析和设计具有重要意义[1,2].传统建模方法一般采用理想变换器模型，控制采用模拟电路实现，这已无法满足当今开关电源的高性能要求[3].通过对相关文献的阅读发现，该变换器是一个带有闭环控制的高阶-离散-非线性-时变复杂系统，其动态模型的准确建立是一个难题[4].近几十年来，有众多国内外研究者对此展开研究，并且取得了不错的成果.开关电源的建模方法主要有4种：状态空间平均法(小信号建模法)[5-7]、电路平均法[8]、等效小参数量法[9]和描述函数法[10].小信号建模为当前最常用的开关变换器动态建模方法.关于双零点-双极点补偿网络，有学者将此补偿网络应用于开关变换器中，对网络零、极点配置方法进行了阐述[11].有学者将它应用于Buck电路中，建立了小信号模型等效电路，运用Matlab对补偿网络和整个电路进行了仿真分析，从阶跃响应和负载扰动上验证了理论分析与设计的正确性，虽尝试了一种新型补偿网络控制器，然而对小信号建模方面没深入研究，给出的仿真波形不甚理想[12].

针对结合小信号模型和新型补偿网络设计二者来研究Buck变换器不多的情况不多，此处基于电感电流连续状态(CCM模式)的模式，详细推导小信号建模的过程，阐述了PD，PID和双极点-双零点3种补偿网络的设计，首先采用PD补偿网络，使得闭环系统的穿越频率和相位裕量满足了要求，但稳态误差还是较大，同时抑制高频干扰的能力不是很强.在此基础上，增加积分环节得到PID补偿网路，解决了PD补偿网络的不足.考虑到滤波电容ESR带来的零点影响，抑制高频干扰的能力不够理想，以及Buck变换器传函的双重零点带来的幅频尖峰的影响，最后在PID补偿网路的基础上再增加一个极点，用原来的PID补偿网络两个零点来抵消双重极点的影响，这样得到双零点-双极点补偿网络.经Matlab仿真，补偿后的开环传递函数伯德图，获得了具有更为优越的动态品质和稳态特性的闭环系统.

1Buck变换器的小信号分析

图1为Buck变换器的主电路，有一个功率管与负载串联而成.但作为调压的直流变换器应用时，输出纹波太大.为了降低输出纹波，输出接入滤波电路，VD为续流二极管，通常变换器的工作频率很高，若电感L足够大，可认为理想元件，电路工作在CCM状态下，进入稳态后，可认为输出电压为恒定值.在工作中，电路输出纹波电压主要是由于滤波电容C的电容有效等值电阻RESR引起的，虽然其值很小，但在开关电源设计中必须要考虑到，相当于在滤波电容C处串联一个阻值很小的电阻RESR.

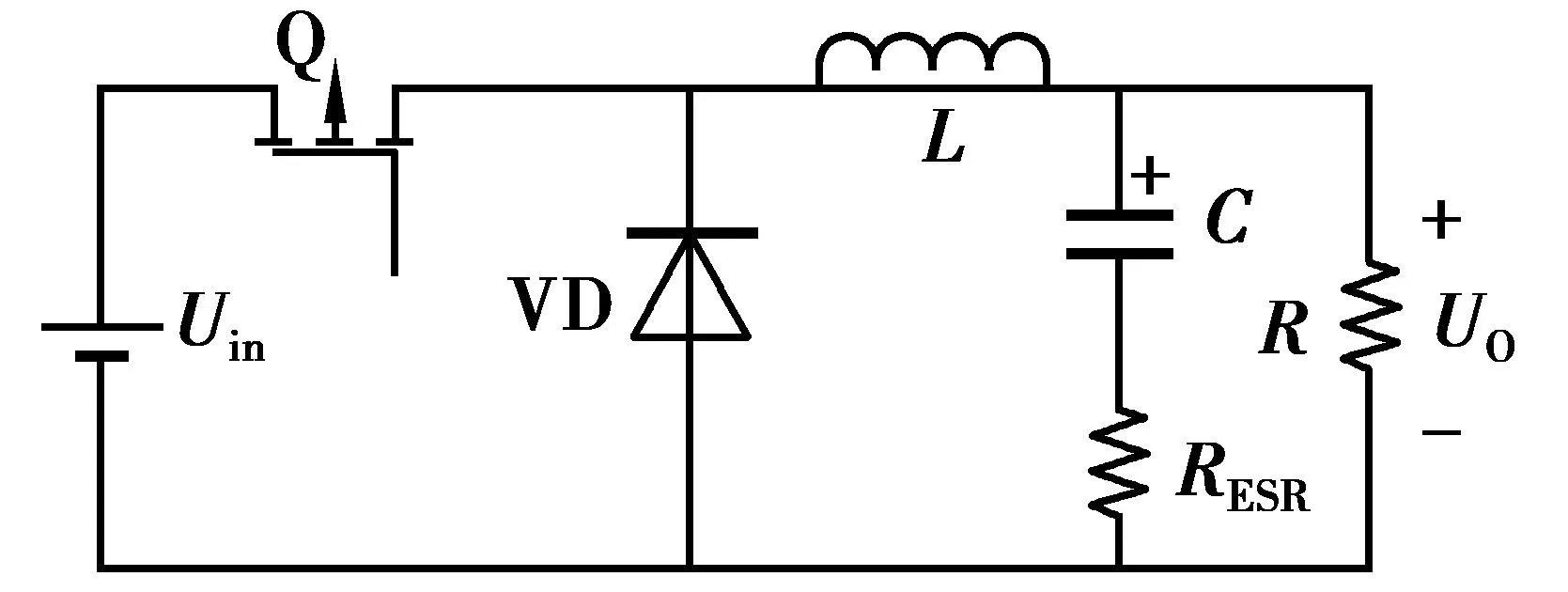
图1　Buck变换器主电路Fig.1　Buck converter main circuit

电感电压状态方程有

(1)

由Buck变换器电路图，知

(2)

由式(1)(2)知

(3)

此时由式(3)，加小信号波动值可建立小信号分析

(4)

由式(3)(4)得

(5)

开关电源在其开关频率的频带范围内，输入电压Uin是不变的，在设计中令Uin=0，且在电感电流连续状态下Uo=DUin，RESR≤R，稳态时Uo=iLR.

故由式(5)经拉普拉斯变换可得主电路控制与输出小信号传递函数.

(6)

2闭环补偿网络的设计

图2为典型的Buck变换器的闭环控制系统.

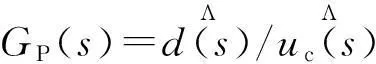
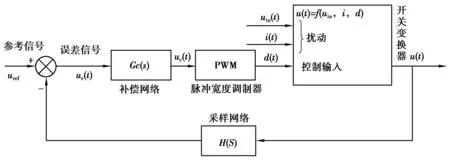
图2　Buck变换器闭环控制系统Fig.2　Closed loop control system of Buck converter

2.1超前补偿(PD)的设计

为了解决比例控制器存在没有相位补偿功能,且会造成一定程度的相位滞后等问题，需要增加相位超前补偿电路，采用PD补偿网络，如图3(a).

PD补偿网络的传递函数为

(7)

2.2超前滞后补偿(PID)的设计

在PD补偿网络上增加倒置零点，即在PD补偿网络的基础上增加积分环节得到PID补偿网络，从而解决了PD补偿网络的不足，PID补偿网络电路，如图3(b).

PID补偿网络的传递函数为

(8)

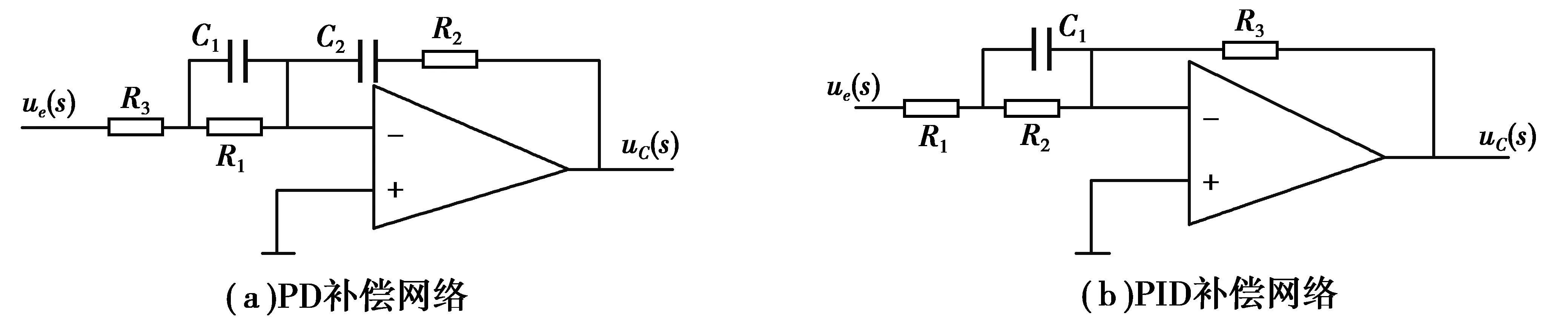
图3　PD,PID补偿网络Fig.3　PD,PID compensation network

2.3双极点-双零点补偿网络的设计

该文采用的闭环控制系统的补偿网络是双极点-双零点补偿网络，在PD和PID补偿网络设计基础上，在PID补偿网络上再增加一个极点，用原来的PID补偿网络两个零点抵消双重极点的影响，这样得到双零点-双极点补偿网络，如图4.

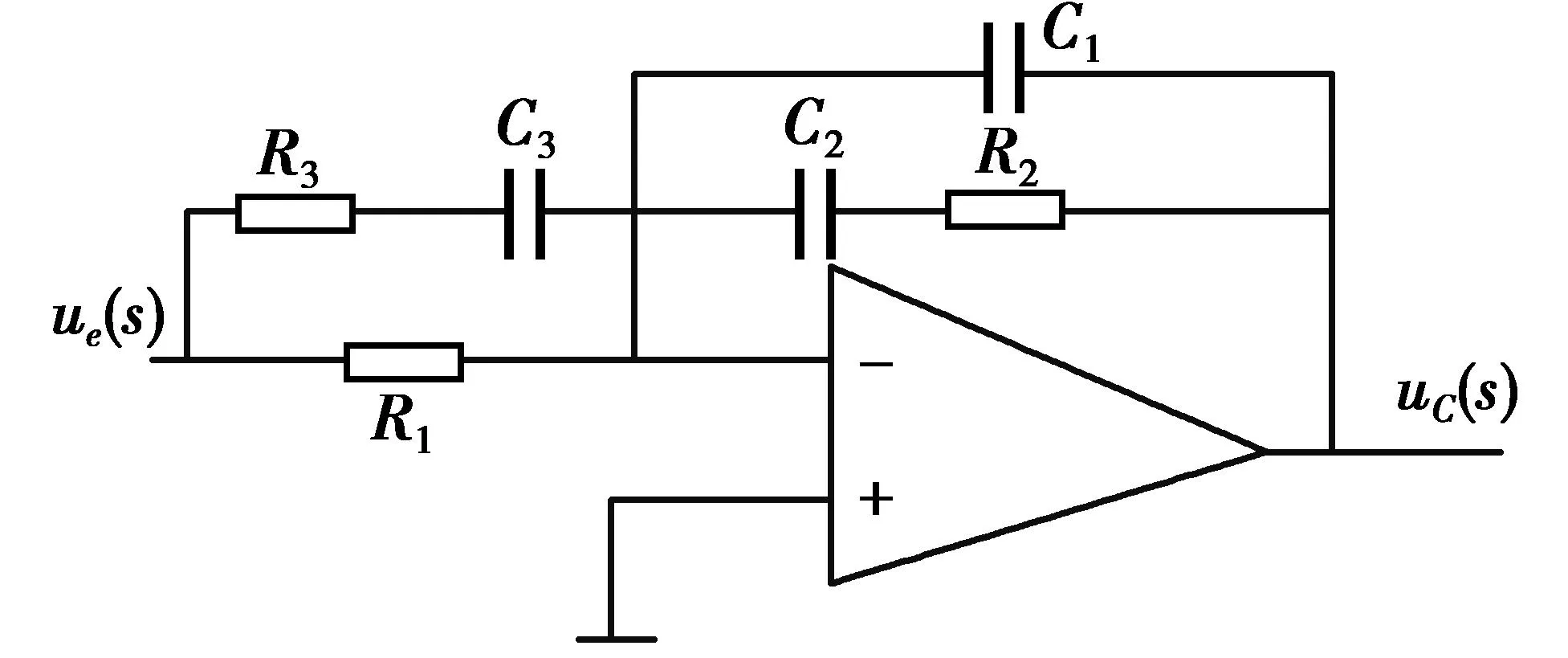
图4　“双极点-双零点”补偿网络Fig.4　Compensation network of double-pole-double -zero

其传递函数为

在此，C2≥C1，C2≥C3，R1≥R3，故ωz1<ωz2<ωp1<ωp2.

所设计的双零点-双极点补偿网络的传递函数为

(9)

经上述设计，补偿后的的开环传递函数为

(10)

其中，Vm为驱动芯片的工作电压，Vg为电路输入电压，ωz0为输出电容ESR引起的零点频率，ωp0为双重极点频率，Q0为品质因数.

3仿真与结果讨论

为了验证上述设计的正确性和实用性，采用了挂接在Matlab 6.5环境上的Simulink进行搭建电路模型和仿真分析，这种实体图形化模型的仿真具有简单、节约设计时间等特点，应用非常广泛.

某车载Buck变换器，开关频率选择为10 kHz，各元件选取为C=6 800 μm，L=8.8×10-3mH，Vg=12 V，R=2.5Ω；RESR=0.01 Ω.

将以上取值代入式(6)得

按照3种补偿网络设计推算，补偿网络元件取值为R1=10 kΩ，R2=10 kΩ，R3=1.3 kΩ，C1=2×10-9F=2 pF，C2=47 nF，C3=47 nF.

代入式(7)(8)(9)(10)，分别得到加补偿网络后系统的开环传递函数：

经Matlab仿真出开环传递函数伯德图，如图5，6，7.图5中，PD补偿网络在范围15.4~62 krad/s(2.45~10 kHz)内，开环传递函数的相位裕量φm都大于45°，但当元件稍有变化时，穿越频率会稍稍偏离5 kHz，对相位裕量影响较小.由于在范围0~0.5 kHz内，幅频特性曲线是平坦的，因此稳态误差大.在高频段曲线是-20 dB/dec，斜率下降，抑制高频干扰的性能不强.PID补偿网络Matlab仿真后，在ωc=2πfc=31.4 krad/s，相位裕量为φm=67°.但在高频段，曲线是以-20 dB/dec下降，抑制高频干扰的能力还是不够强.

用开环伯德图判定闭环系统是稳定的.从图6中可以显示出，相角裕度为51.1°(大于45°)，比原来的32.7°大，可见加补偿网络后系统稳定性提高.采用双零点-双极点补偿网络与PID补偿网络一样在低频段提供了一个极点，其稳态误差为零.由图7可以看出，双零点-双极点补偿网络的第一个极点是用来抵消输出电容的零点，第二个极点用来保证开环传函有一个较好的相位裕度和增益裕度.同时在高频段，幅频特性的下降频率为-40 dB/dec，对高频具有很好的抑制作用.与PID和PD补偿网络相比具有更好的抑制高频干扰的能力.

图5　PD和PID补偿网络的开环传递函数伯德图的比较Fig.5　Bode diagram comparison between PD and PID compensation network

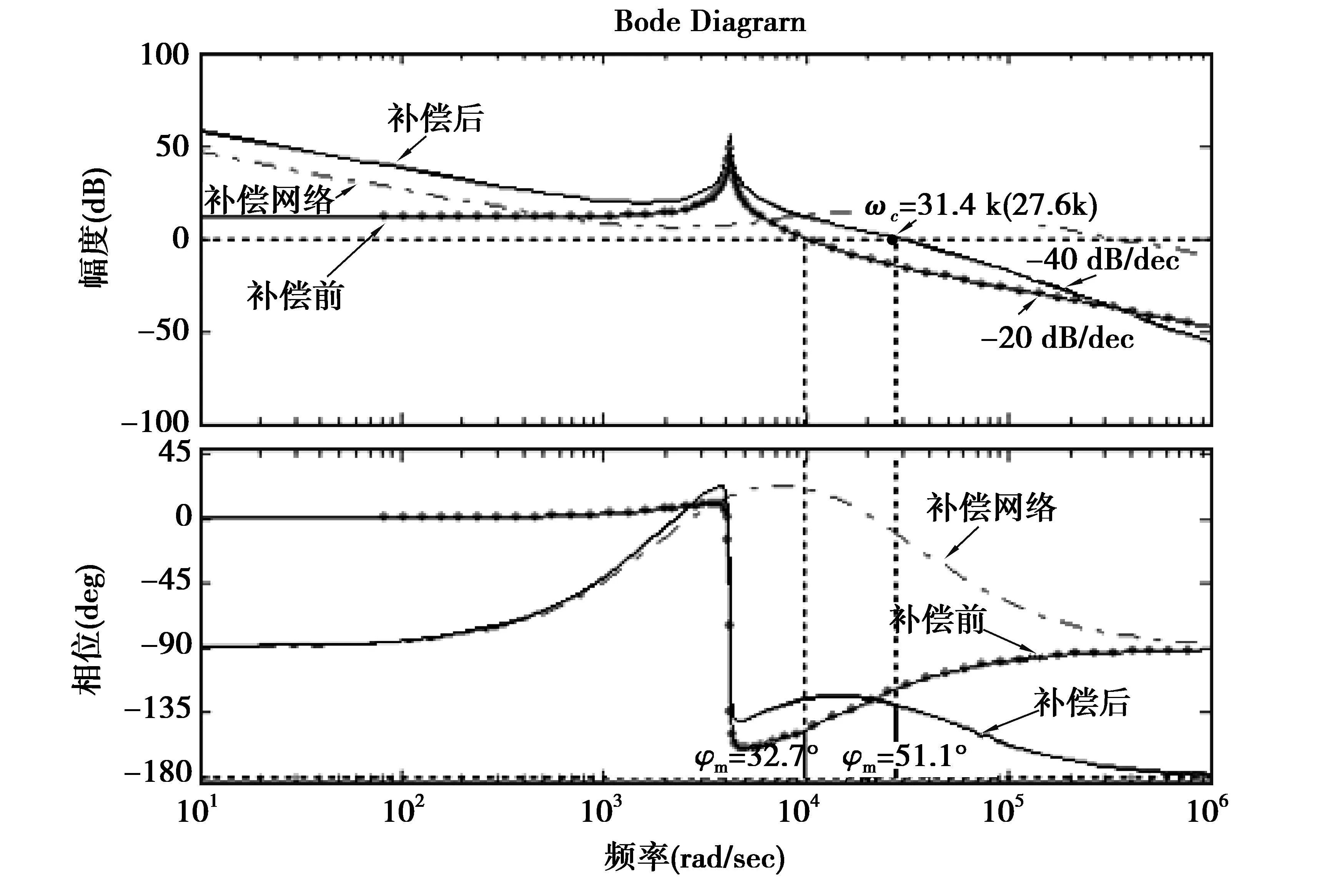
图6　双零点-双极点补偿网络前后的开环传递函数伯德图的比较Fig.6　Open-loop-function Bode comparison of double-pole-double-zero

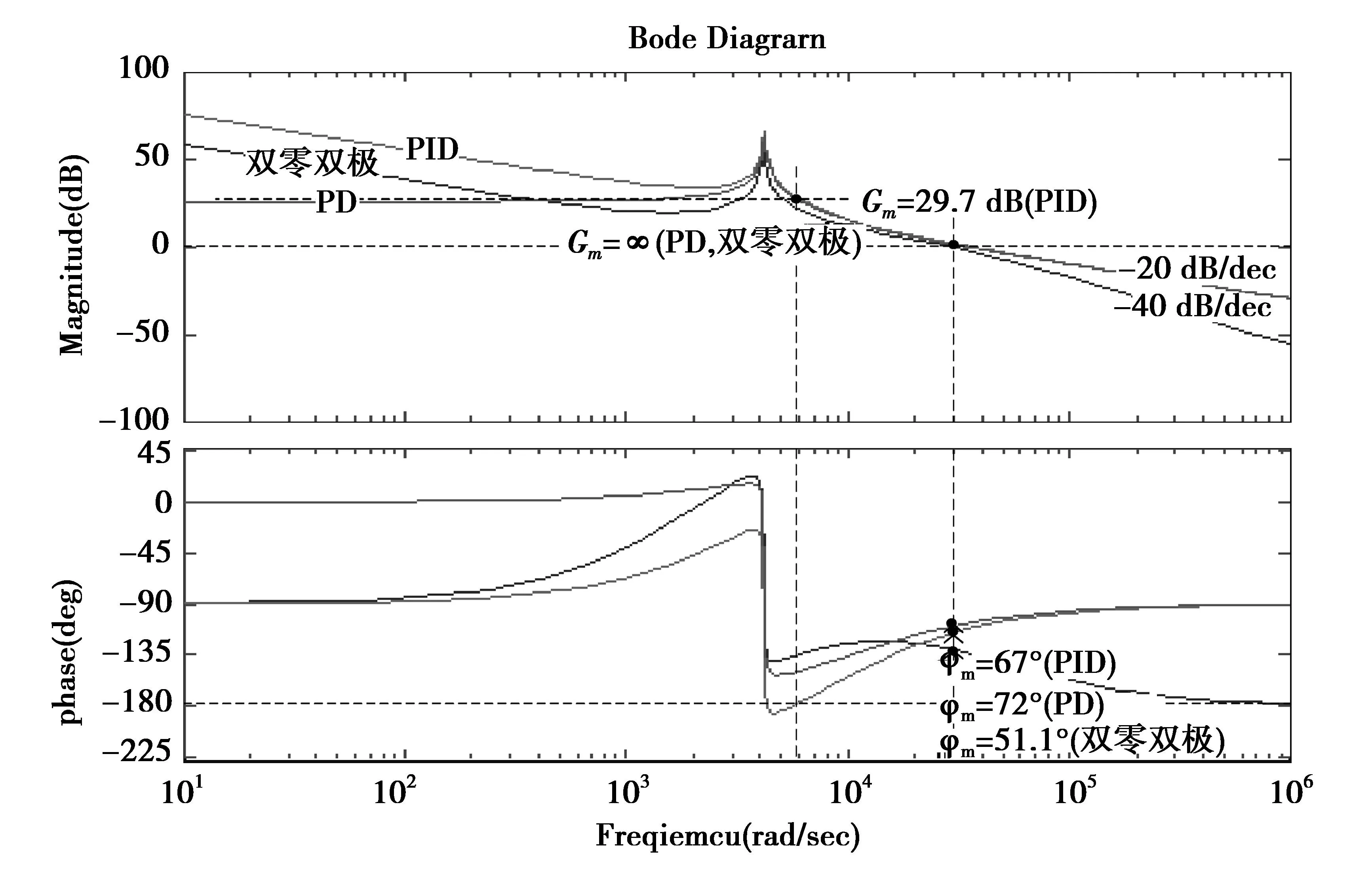
图7　双零点-双极点、PID和PD补偿网络得出的开环伯德图的比较Fig.7　Open-loop Bode comparison between PD and PID compensation network

4结论

在对Buck变换器的小信号建模分析的基础上，先后设计了PD，PID补偿网络和新型双零点-双极点补偿网络，对系统仿真出的各自开环传递函数伯德图的比较得出，双零点-双极点补偿网络相位和增益裕度较好，体现了稳态误差低，稳态和动态性能更好，对高频有更好的抑制等特点，验证了小信号建模分析和新型补偿网络设计的正确性，设计思路可以应用到其他开关电源中.

参考文献(References)：

[1]DONG M.Designing Stable Compensation Network for Single Phase Voltage Mode Buck Regulators[R].Intersil Technical Brief,2003

[2] 邵桂荣,苏世栋,詹平红.DC-DC开关变换器的动力学建模与稳定性分析[J].重庆理工大学学报(自然科学版),2010,24(11):93-96

SHAO G R,SU SH D,ZHAN P H.Dynamic Modeling and Stability Study of DC-DC Switching Converter[J].Journal of Chongqing University of Technology(Naturnal Science Edition),2010,24(11):93-96

[3] 宣传,徐慧芳,解光军.CCM模式下非理想Buck变换器的建模和仿真[J].电子器件,2012,35(1):70-74

XUAN C,XU H F,XIE G J.Modeling and Simulation of Non-ideal Buck Converters Operating in CCM[J].Journal of Electron Devices,2012,35(1):70-74

[4] 王英武,王俊峰,刘佑宝，等.DC/DC变换器小信号建模与补偿网络设计[J].电力电子技术,2009,43(3):26-28

WANG Y W,WANG J F,LIU Y B，et al.Small-signal Equivalent Circuit Modeling and Compensation Network Design of DC/DC Converter[J].Power Electronics,2009,43(3):26-28

[5] 潘小波,宁平华,夏兴国.BUCK电路的状态分析与仿真研究[J].齐齐哈尔大学学报(自然科学版),2015,31(5):33-38

PAN X B,NING P H,XIA X G.Working State Analysis and Simulation Research on BUCK Circuit[J].Journal of Qiqihar University(Naturnal Science Edition),2015,31(5):33-38

[6] 曹雪,乔科佳,付光杰.带补偿网络的Buck变换器小信号模型[J].电气开关,2011(3):40-43

CAO X,QIAO K J,FU G J.The Small Signal Model of Buck Converter with Compensating Network[J].Journal of Electrical switches,2011(3):40-43

[7] GAZINEU R,QUEVEDO C A.Non-linear Controller Applied to Boost DC-DC Converters Using the State Space Average Model[C].Power Electronics Conference,IEEE,2009:734-740

[8] ABRISHAMIFAR A，RAHMATI S M，KHAZRAEI.Small Signal and Large Signal Charge Control Models for a Phase-Shifted PWM Converter[C]∥IEEE International Conference on Industrial Technology,2008:1-6

[9] QIU S S,FILARMSKY L M,LIN B T.A New Method of Analysis for PWM Switching Power Converter[J].IEEE Int J of Electronics,1999,86(11):1395-1410

[10]QIAN Z J,ABDEL-RAHMAN O,AL-ATRASH.Modeling and Control of Three-Port DC/DC Converter Interface for Satellite Applications[J].IEEE Transactions on Power Electronics,2010,25(3):637-649

[11] 章赛军,杨永宏,柯建兴,等.电压反馈型Buck变换器环路补偿设计[J].通信电源技术,2004,21(6):4-6

ZHANG S J,YANG Y H,KE J X,et al.Design of Compensation Network for Voltage Mode Buck Regulators[J].Telecom Power Technologies,2004,21(6):4-6

[12] 司伟.基于MATLAB设计电压型Buck变换器[J].科技信息,2011(3):360-362.

SI W.Design of Voltage Mode Buck Converter Based on MATLAB[J].Science & Technology Information,2011(3):360-362

[13] 王金龙,张方华,张帅.高效率准谐振Buck变换器设计与研究[J].电工电能新技术,2014,33(4):11-15

WANG J L,ZHANG F H,ZHANG S.Design and Study of High Efficiency Quasi Resonant Buck Converter[J].Advances Technology of Electrical Engineering & Energy,2014,33(4):11-15

[14](美)ABRAHAM I,PRESSMAN,KEITH B,等.开关电源设计[M].3版.王志强等译.北京:电子工业出版社,2013

ABRAHAM I.PRESSMAN,KEITH BILLINGS,,et al.Switching Power Supply Design[M].3rd ed.WANG Zhiqiang,et al.Translation.BeiJing:Electronic Industry Press，2013

责任编辑：李翠薇

Design of a Novel Buck Converter Compensation NetworkBased on Small Signal Model

XIA Xing-guo1, CHEN Le-zhu2, PAN Xiao-bo1, ZHANG Qing-feng1

(1.Department of Electrical Engineering, Maanshan Technical College, Anhui Maanshan, 243031,China;

2.School of Electrical and Information Engineering, Anhui University of Technology, Anhui Maanshan, 243002, China)

Abstract：The main circuit of Buck converter is analyzed in CCM mode, and the small signal model is derived in detail. Three kinds of closed-loop control compensation networks have been designed and named PD, PID and the “double-pole and double-zero” compensation networks. This paper derived the system of the open-loop transfer function after compensation network, and simulated the Bode plot of the open-loop transfer function before and after the compensation network in matlab. The results indicated that the phase margin was 51.5 degrees, the steady-state error was zero, and the down frequency of amplitude-frequency characteristics was -40dB/dec at high frequencies after“double-pole and double-zero” compensation network. The results had better stability and dynamic performance, and better suppress in high frequency interference. The result has a very good reference for further research of other switching power supply.

Key words：Buck converter; compensation network; inductor current continuous mode; small signal model; double-pole and double-zero

中图分类号：TN624

文献标志码：A

文章编号：1672-058X(2016)01-0052-07

作者简介：夏兴国(1983-)，男，安徽当涂人，讲师，硕士研究生，从事电力电子及其控制技术、自动化控制技术研究.

*基金项目：安徽省高校省级优秀青年人才基金重点项目(2013SQRL145ZD).

收稿日期：2015-10-13；修回日期：2015-11-20.

doi:10.16055/j.issn.1672-058X.2016.0001.012