关于不定方程x(x+1)(x+2)(x+3)=30y(y+1)(y+2)(y+3)*

王　聪

(西南大学 数学与统计学院，重庆 400715)



关于不定方程x(x+1)(x+2)(x+3)=30y(y+1)(y+2)(y+3)*

王聪

(西南大学 数学与统计学院，重庆 400715)

摘要：主要运用Pell方程、递归数列、同余式及平方(非)剩余等一些初等方法，证明了不定方程x(x+1)(x+2)(x+3)=30y(y+1)(y+2)(y+3)无正整数解.

关键词：不定方程；整数解；递归数列

设p是素数，对于形如

的不定方程曾引起很多人的研究兴趣[1-7].此处将证明当p=30时的情况，即不定方程

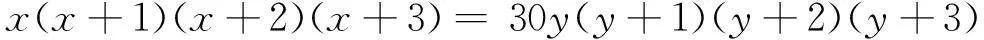
(1)

无正整数解.

先将式(1)化为如下形式：

(x2+3x+1)2-30(y2+3y+1)2=-29

(2)

易知方程x2-30y2=-29的全部整数解由以下两个(非结合)类给出：

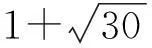
(3)

(4)

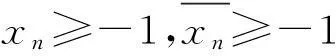
不难推出下列关系式：

(5)

(6)

(7)

(8)

(9)

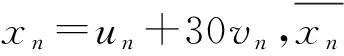
(10)

(11)

(12)

将证明式(3)仅当n=0，1时成立，式(4)仅当n=0时成立，由此求得方程(x2+3x+1)2-30y2=-29的全部整数解，可作为推论得到p=30时方程(1)的全部正整数解.

1(2x+3)2=4xn+5

考察式(3)的解，即n取何值时4xn+5为完全平方数.

引理1设2|n,n>0,则

引理2设n≡0(mod 84)，且n>0，则式(3)不成立.

i)k≡1(mod 4).令

则有表1：

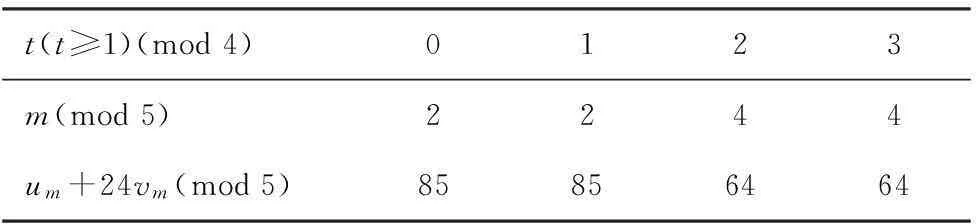
表1　k≡1(mod 4)情况下的数据

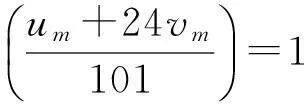
4xn+5≡4x2m+5≡120v2m+5(modu2m)

从而

所以4xn+5为非平方数，故式(3)不成立.

ii)k≡-1(mod 4).令

则有表2：

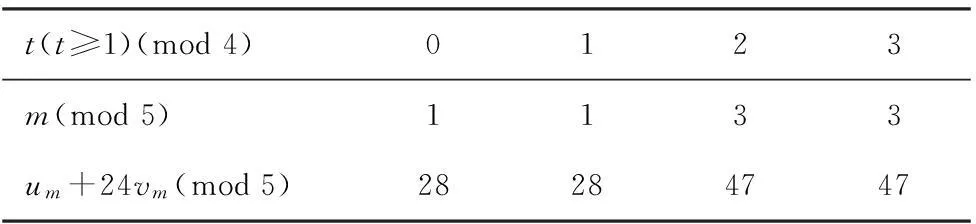
表2　k≡-1(mod 4)情况下的数据

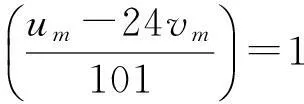
从而

所以4xn+5为非平方数，故式(3)不成立.

引理3设n≡1(mod 12)，且n>1，则式(3)不成立.

证明令n=1+2·3rm,r≥0,2|m,3|m，则m≡±6,±12(mod 32)，由式(12)，4xn+5≡-4x1+5≡-279(modum)，得

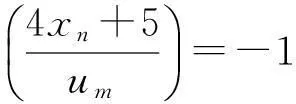
推论1设n≡0,1(mod 84)，且n>1，则式(3)不成立.

引理4若式(3)成立，则必需n≡0,1(mod 84).

证明采用对序列4xn+5取模的方法来证明.

mod 29，排除n≡2,4,6,8,11,12,13(mod 14)，此时4xn+5≡14,18,27,11,21,10,12(mod 29),剩n≡0,1,3,5,7,9,10(mod 14).

mod 349，排除n≡5,9(mod 14)，此时4xn+5≡133,43(mod 349),剩n≡0,1,3,7,10(mod 14).此等价于n≡0,1,3,7,10,14,15,17,21,24,28,29,31,35,38(mod 42).

mod 41，排除n≡3,15,17,28,38(mod 42)，此时4xn+5≡26,29,22,6,29(mod 41).

mod 463，排除n≡14,24,29(mod 42)，此时4xn+5≡157,432,176(mod 463).

mod 881，排除n≡35(mod 42)，此时4xn+5≡94(mod 881),剩n≡0,1,7,10,21,31(mod 42).此等价于n≡0,1,7,10,21,31,42,43,49,52,63,73(mod 84).

mod 503，排除n≡7,10,31,49,52(mod 84)，此时4xn+5≡151,109,491,362,404(mod 503).

mod 1 091，排除n≡21,43,63,73(mod 84)，此时4xn+5≡878,812,223,925(mod 1091),剩n≡0,1,42(mod 84).

mod 4 703，排除n≡14,42(mod 56)，此时4xn+5≡1 260,3 453(mod 4 703)，故式(3)不成立.

从而排除n≡42(mod 84)，剩余n≡0(mod 84).

对式(4)进行讨论.

引理5设n≡0(mod 84)，且n>0，则式(4)不成立.

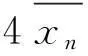
引理6 若式(4)成立，则必需n≡0(mod 84).

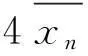
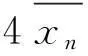
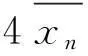
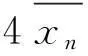
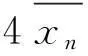
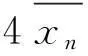
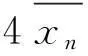
3结果

根据前两节的讨论，现在可给出主要结果.

定理1不定方程

(x2+3x+1)2-30y2=-29

(13)

的全部整数解是 (x,±y)=(0,1),(-3,1),(7,13),(-10,13),(-1,1),(-2,1).

证明由推论1和引理4知若式(3)成立，必需n=0,1，此时x=0,-3,7,-10，这给出方程(13)的前4组解.又由引理5和引理6知若式(4)成立，必需n=0，此时x=-1,-2，这给出方程(13)的后2组解.

作为定理1的推论，得到

定理2不定方程

(14)

无正整数解.

证明由式(2)和定理1，应有y2+3y+1=±13，但这两个方程都无正整数解，从而方程x(x+1)(x+2)(x+3)=30y(y+1)(y+2)(y+3)无正整数解.

参考文献(References)：

[1]COHN J.The Diophantine Equationx(x+1)(x+2)(x+3)=2y(y+1)(y+2)(y+3)[J].Pacific J Math,1971,37:331-335

[2] PONNUDURAI T.The Diophantine Equationx(x+1)(x+2)(x+3)=3y(y+1)(y+2)(y+3)[J].J London Math Soc,1975(10):232-240

[3] 宣体佐.关于不定方程x(x+1)(x+2)(x+3)=5y(y+1)(y+2)(y+3)[J].北京大学学报(自然科学版)，1982(2)：27-34

XUAN T Z.On the Diophantine Equationx(x+1)(x+2)(x+3)=5y(y+1)(y+2)(y+3)[J].Journal of Beijing Normal University(Natural Science Edition),1982(2):27-34

[4] 罗明.关于不定方程x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)[J].重庆师范学院报(自然科学版)，1991,8(1)：1-8

LUO M.On the Diophantine Equationx(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)[J].Journal of Chongqing Normal University(Natural Science Edition),1991,8(1):1-8

[5] 程瑶，马玉林.关于不定方程x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)[J].重庆师范大学学报(自然科学版),2007(1)：27-30

CHENG Y,MA Y L.On the Diophantine Equationx(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)[J].Journal of Chongqing Normal University(Natural Science Edition),2007(1):27-30

[6] 罗明，郭凤明.关于不定方程x(x+1)(x+2)(x+3)=13y(y+1)(y+2)(y+3)[J].重庆师范大学学报(自然科学版)，2014,30(5):101-105

LUO M,GUO F M.On the Diophantine Equationx(x+1)(x+2)(x+3)=13y(y+1)(y+2)(y+3)[J].Journal of Chongqing Normal University(Natural Science Edition),2014,30(5):101-105

[7] 张洪,罗明.关于不定方程x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(D=21,23)[J].重庆工商大学学报(自然科学版)，2015,32(7):56-61

ZHANG H，LUO M.On the Diophantine Equationx(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(D=21,23)[J].Journal of Chongqing Technology and Business University(Natural Science Edition),2015,32(7):56-61

[8] 柯召，孙琦.谈谈不定方程[M].哈尔滨：哈尔滨工业大学出版社，2011

KE Z,SUN Q.About Indeterminate Equation[M].Harbin:Harbin Institute of Technology Press,2011

责任编辑：李翠薇

On the Diophantine Equationx(x+1)(x+2)(x+3)=30y(y+1)(y+2)(y+3)

WANG Cong

(School of Mathematics and Statistics, Southwest University, Chongqing 400715, China)

Abstract：In this paper, with the method of pell equation, recurrence sequences, congruence and square non-residual and so on, we have shown that the Diophantine equation x(x+1)(x+2)(x+3)=30y(y+1)(y+2)(y+3) has no positive integer solution.

Key words：Diophantine equation; integer solution; recurrence sequence

中图分类号：O156.2

文献标志码：A

文章编号：1672-058X(2016)01-0029-04

作者简介：王聪(1991-)，女，河南濮阳人，硕士研究生，从事计算数论研究.

*基金项目：国家自然科学基金资助(11471265).

收稿日期：2015-09-13；修回日期：2015-10-30.

doi:10.16055/j.issn.1672-058X.2016.0001.007