关于p次幂平均函数对数凸性的探讨

官 春 梅

(喀什大学 数学与统计学院,新疆 喀什 844006)



关于p次幂平均函数对数凸性的探讨

官 春 梅

(喀什大学 数学与统计学院,新疆 喀什 844006)

摘要：众所周知，两个正实数a与b的p次幂平均函数为 .证明了当p≤0时，幂平均函数Mp(a,b)关于参变数p是凸的; 进一步，在p≤0和p≥0时，幂平均函数Mp(a,b)关于参变数p还分别是对数凸及对数凹的.

关键词：幂平均函数；对数凸性；偏导数

1知识回顾

一直以来，幂平均函数始终是中学数学重点研究的主题之一.所谓两个正实数a与b的p次幂平均函数Mp(a,b)被定义为

其中参变量p∈R.为此，可从文献中找到有关Mp(a,b)的众多优美不等式，包括其他类型均值函数的不等式.

对固定的a,b>0，a≠b和p∈R，Mp(a,b)是参变量p的严格递增连续函数[1].同时，Mp(a,b)=aMp(1,b/a).Mildorf[2]研究了函数

并证明了对任给的正实数a和参变量p∈R，分别有

(A) 当p≥1时，f(p,a)关于p是凹的;

(B) 当p≤-1时，f(p,a)关于p是凸的.

此处将进一步研究幂平均函数Mp(a,b)关于参变量p的对数凸性.在此基础上，推广了一些已知的均值不等式.

2判别定理

定理1如果令f(p,a)=Mp(1,a)，那么下列结论成立:

(i) 当p≤0时，函数f(p,a)是对数凸的;

(ii) 当p≥0时，函数f(p,a)是对数凹的;

(iii) 当p≤0时，函数f(p,a)是凸的.

证明直接验证可知，对任意实数t，都有

(1)

在式(1)两边取对数，并令g(p,a)=lnf(p,a)可得tg(pt,a)=g(p,at)，对p分别求一阶和二阶导数有

(2)

特别地，在式(2)中取p=1，可得

(3)

由Mildorf所获得的结论(A)可知，g(p,a)关于参变量p单增且当p≥1时为凹函数.因此，对∀a>0和t∈R，g″11(1,at)≤0.

现在，讨论式(3)左边的函数.由于t3g″11(t,a)≤0，所以当p>0时，g(p,a)关于p是凹的.在此情况下，f(p,a)关于p对数凹，并且当p<0时，g(p,a)关于p是凸的.这就证明了结论(i)与(ii)成立.显然，由结论(i)立即可得结论(iii)成立.

3推广

下面，利用定理1的结论，给出一些已知均值不等式的推广.由定理1的结论(iii)立即可得推论1.

推论1对所有a,b>0，α∈[0,1]和p,q≤0，均值不等式

(4)

成立.

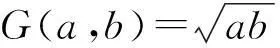
该均值不等式的另一种证明可参见文献[3].

由定理1的结论(ii)直接可得下面的均值不等式.

推论2对所有a,b>0，α∈[0,1]和p,q≥0，均值不等式

(5)

成立.

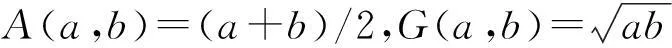
(6)

和式(5)，可得

(7)

特别地，在式(7)中若取p=1或p=0，则可以分别得到下面的两个均值不等式

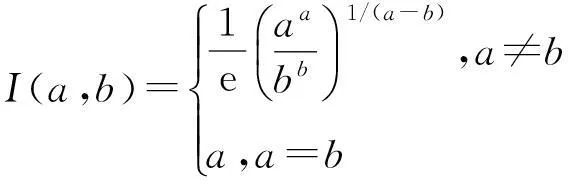
(8)

联合使用式(5)，(6)和(8)，可得

(9)

借助定理1的帮助，还可以证明更多其他类似的均值不等式，在此就不赘述了.

参考文献(References)：

[1]王继岳，徐沥泉.幂平均函数及其平均不等式[J].数学通报，1985(6)：45-46

WANG J Y，XU L Q.Power Mean Function and Its Inequality[J].Mathematics Bucletin,1985(6)：45-46

[2] Mildorf T J.A Sharp Bound on the Two Variable Powers Mean[J].Mathematical Refiections,2006,(2):3-7

[3] CHU Y M,XIA W F.Two Sharp Inequalities for Power Mean,Geometric Mean and Harmonic Mean[J].Journal of Inequalities and Applications,2009(1155):1-6

[4] 廖秋根.与幂平均相关的若干不等式[D].长沙：湖南大学，2010

LIAO Q G.Some Inequalities Related to power Mean[D].Changsha:Hunan University,2010

[5] 王姗姗.一个平均值不等式[J].湖州师范学院学报， 2010，32(1):38-41

WANG SH SH.An Inequality for Means[J].Journal of Huzhou University,2010，32(1):38-41

责任编辑：李翠薇

Discussion on Logarithm Convexity of pth Power Mean Function

GUAN Chun-mei

(School of Mathematics and Statistics, Kashgar University, Xinjiang Kashgar 844006, China)

Abstract：It is well-known that the pth power mean function of two positive real number a and b is defined as Mp(a,b)=((aspan+bspan)/2)1/,p≠0 while p=0. This paper proves that power mean function Mp(a,b) is convex for parameter p≤0, that furthermore, power mean function Mp(a,b) is log-convex for parameter p≤0 and is log-concave for parameter p≥0 respectively.

Key words：power mean function; logarithmic convexity; partial derivative

中图分类号：O178

文献标志码：A

文章编号：1672-058X(2016)01-0023-03

作者简介：官春梅(1976-)，女，湖北省竹山人，讲师，研究生学历，从事基础数学研究.

收稿日期：2015-09-04；修回日期：2015-10-23.

doi:10.16055/j.issn.1672-058X.2016.0001.005