半无限长弦振动问题的讨论*

刘　岩

(兰州财经大学 信息工程学院，兰州 730020)



半无限长弦振动问题的讨论*

刘岩

(兰州财经大学 信息工程学院，兰州 730020)

摘要：讨论了半无限长弦的自由振动问题和强迫振动问题,在牛顿定律的基础上建立了弦振动方程并进行了求解;结果表明强迫振动下各质点的振动位移与时间的关系要复杂得多,它不仅与边界点x=0处的振动有关，还与力密度有直接的关系.

关键词：弦振动方程;定解问题;达朗贝尔公式;延拓

弦振动问题是数学物理的经典问题之一.所谓弦振动问题，是对弦上各点位移在空间的特定区域中的分布情况以及随时间变化情况的研究.

1747年,达朗贝尔关于弦振动的著名研究，导出了弦振动方程及其最早的解，成为偏导数方程论的发端.通过对琴弦横向振动逆命题的研究，得到柔索的张紧力与索的密度、索横向振动的固有频率、索的长度有关,应用这个理论可以对大型斜拉桥的索力、体育馆的吊索力以及特大型水坝的起吊闸门的索力等进行检测,并可以识别吊索故障.弦振动力学的学科特点和发展规律对振动力学的研究和教学都有所启发和助益.通过应用声电转换分对弦振动的研究，可以通过测定弦振动的频率对乐器进行调音.通过建立弦振动模型，导出了输电带张力和转速的匹配关系.应用弦振动理论建立了计及某自动行火炮自动供弹机链传动机构的啮合冲击和多边形效应的横向振动模型，并编制了相应的计算程序，进行仿真计算,得出了自动供弹机横向振动的定性分析结果.综上所述，弦振动理论及模型在现实生活中的应用是十分广泛的，在工程设计中提供了必要的数据，在科研、技术和其他方面都发挥着巨大的作用[1，2].

1弦振动方程的建立及其解法

1.1一维弦振动方程的建立

条件：设弦是均匀的、柔软的，所谓柔软，即在放松条件下可把弦弯成任意形状，它都保持静止，但在绷紧的情况下，相邻小段之间有拉力，称为张力.假设弦是很轻的，它的重力只是张力的几万分之一，与张力相比，弦的重力可以略去.

设弦的长度为l，密度为ρ，把它绷紧固定在OL上，在不振动时是一条直线，取直线的方向为x轴，如图1所示,当它在平衡位置附近作垂直于x轴的微小振动时，研究弦上各点的位移u与坐标x及时间t的关系即u=u(x,t).

(1) 分段：把弦分成许多极小的小段，任取一段MM′：(x,x+Δx),研究它的情况.

(2) 受力分析：假设作用于弦上的横向外力的线密度为F(x,t)，则MM′段所受外力为：F(x,t)Δx.如果受到邻段的张力T和T′(图1)，由于不考虑重力，而且振动只是横振动.

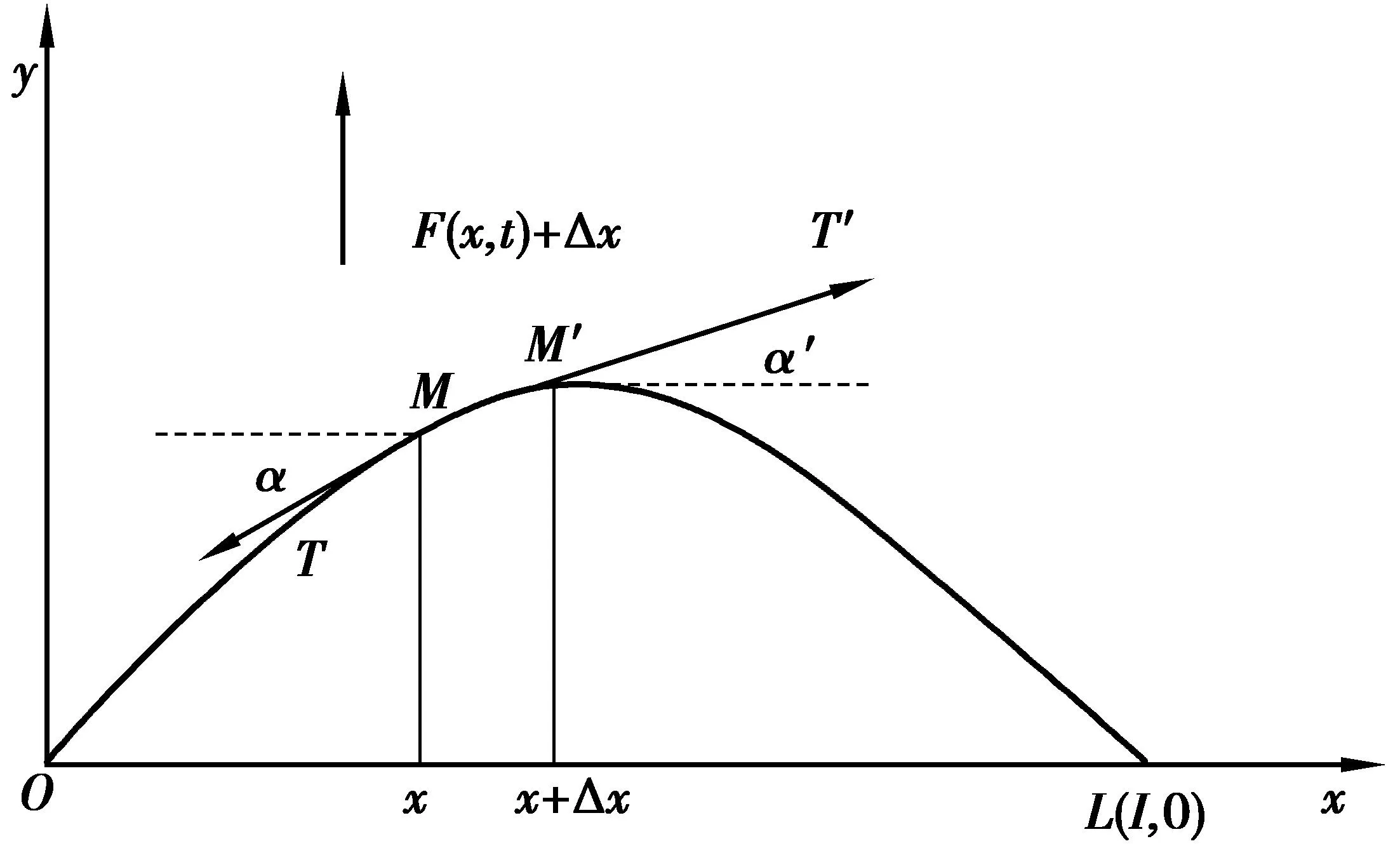
图1　弦上任意部分的受力分析Fig.1　Any part stress on string analysis

作用在MM′上纵向合力为零，即：

T′cosα′-Tcosα=0

横向合力为

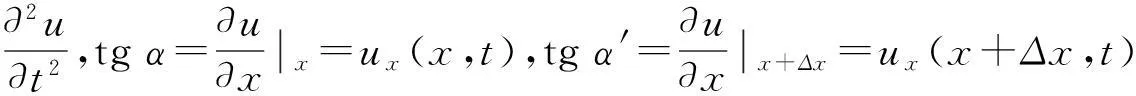
有：

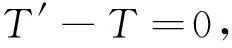
由方程组可得：T=T′即张力不随地点而异，它在整根弦中取同一数值.代入方程可得：

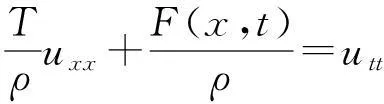
如果弦不受外力作用，即f=0，则方程为：utt-a2uxx=0，为弦的自由横振动方程.其中,a是振动传播的速度[3].

1.2弦振动方程的解法

通常采用分离变量法求解弦振动方程，但不同的问题也有不同的解法，例如无限长弦和半无限长弦的自由振动用达朗贝尔公式法去求解更为简单.[3-6]

下面以无限长弦的自由振动问题为例说明达朗贝尔公式的求解法.

一根无限长的均质柔软轻弦在初始条件作用下所引起的自由横向振动在弦中的传播的情况，其定解问题为

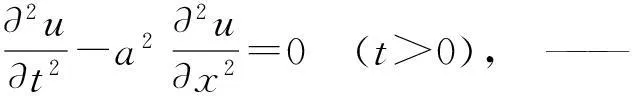
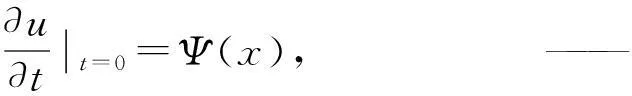
其中u(x,t)表示在时刻t弦上x点的横向位移.(此定解问题中不包含边界条件，是因为此弦是无限长的，所以没有边界，弦上每一点的振动规律都满足弦振动方程.)

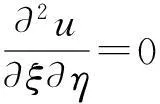
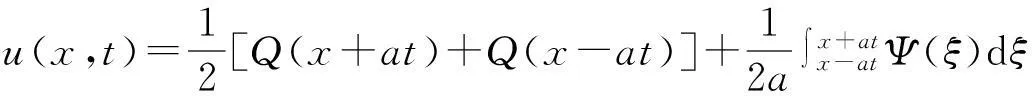
如果将公式写成如下形式：

这样就对达朗贝尔公式中各项的物理含义有一个清晰的理解.第一项是以速度a向左传播的波，第二项是以速度a向右传播的波.u(x,t)的形式说明了弦上任一点的振动都会引起两个相反方向的波动，那么任一点的振动位移u(x,t)应是两种波动分别引起的振动位移的叠加.

2半无限长弦振动问题的具体分析

2.1半无限长弦的自由振动问题

设有一个半无限长的弦，一个端点在x=0处，初始静止在x轴上，在端点x=0处，弦的位移是Asinωt≥0,ω是常数，求弦在任何时刻t在点x处的位移.

设所求的位移是u(x,t)，其定解问题是：

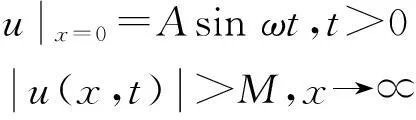
根据无限长弦振动方程的解，可以把这根半无限长弦当作某根无限长弦的x≥0的部分，由初始条件可知，在半无限长弦的振动过程中，点x=0处为振源，那么在x<0区间内各点必须保持不变.可以把半无界区间做延拓到整个无界区间，再应用达朗贝尔公式求解无限长弦的自由振动.它的x≥0的部分正是考察的半无限长弦.

作延拓后，方程组为

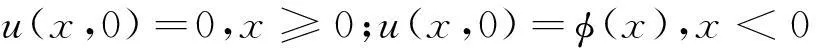
Q(x)0=,x≥0

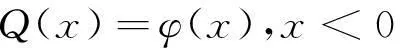
在x<0区间内各点必须保持不变，取ψ(x)=0,x<0可得：

Q(x)=0,x≥0

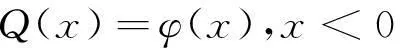
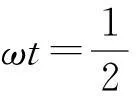
由此可得出：

Q(x-at)=0,x-at≥0

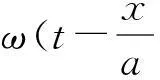
Q(x+at)=0,x+at≥0

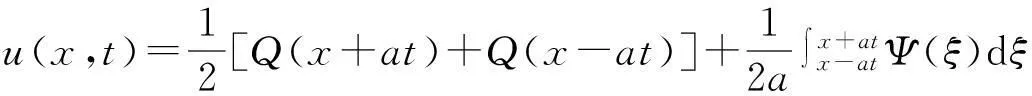
x-at<0,x+at<0时；

x-at<0,x+at≥0时；

u(x,t)=0,x-at≥0,x+at≥0时.

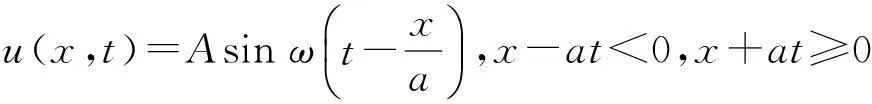
u(x,t)=0,x-at≥0,x+at≥0时.

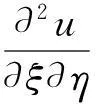
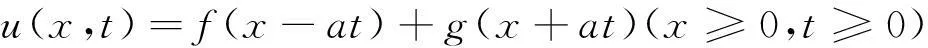
由边界条件和初始条件可得：

(1)

(2)

(3)

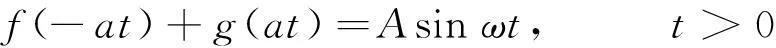
(4)

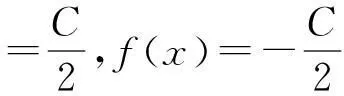
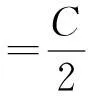
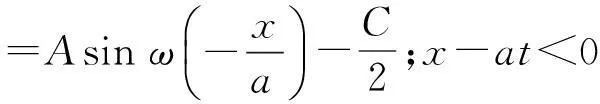
(5)

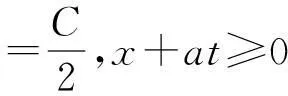
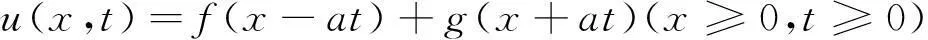
得:

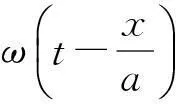
u(x,t)=0(x+at≥0,x-at>0).

2.2半无限长弦的强迫振动问题

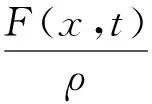
设所求的位移是u(x,t)，其定解问题是：

utt-a2uxx=tsinx,x>0,t>0

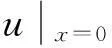
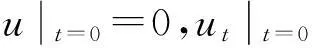
作特征变换ξ=x+at,η=x-at，则方程化为

分别对ξ,η积分，并代入原变量，求得通解

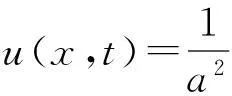
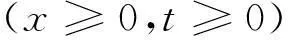
由初值条件得：

(6)

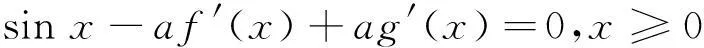
(7)

由式(7)得：

(8)

联立式(6)和式(8)解得：

(9)

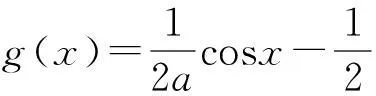
(10)

为了利用通解，须求出在x<0时f(x)的表达式.利用边界条件，有：

f(-at)+g(at)=Asinωt,t≥0

即

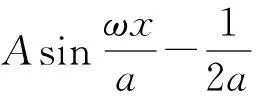
所以

(11)

把式(9)(10)(11)代入通解得所求定解问题的解为

3结论

基于达朗贝尔公式，对非齐次边界条件下半无限长弦的自由振动进行了延拓求解，结果表明弦振动时，波因受到边界点x=0的影响而沿x轴正向传播，即右传播波.用特征量代换的方法对半无限长弦的强迫振动也进行了求解，结果表明强迫振动下各质点的振动位移与时间的关系比自由振动复杂得多，不仅与边界点x=0处的振动有关，而且与力密度有直接的关系.

参考文献(References)：

[1]梁昆淼.数学物理方法[M].南京：高等教育出版社，1998

LIANG K M.Mathematical Physics Method(Simplified Chinese Third Edition) [M].Nanjing:Higher Education Press,1998

[2] 吴崇试.数学物理方法[M].北京：北京大学出版社，2003

WU C S.Mathematical Physics Method (Simplified Chinese Second Edition) [M].Beijing:Peking University press,2003

[3] 竺江峰.对半无限长弦振动问题的讨论[J].牡丹江教育学院学报，2004(3):17-18

ZHU J F.Discussion on the Vibration of Half-infinite of Long Chord[J].Journal of Mudanjiang College of Education,2004(3):17-18

[4] 臧涛成 潘涛.非齐次边界条件时的半无界弦自由振动问题[J]. 大学物理，2006(10):47-49

ZANG T C,PAN T.Free Vibration of Semi-boundless string with inhomogeneous boundary[J].College physics,2006(10):47-49

[5] 周青青. 无限长与半无限长弦振动的分离变量解法[J]. 中国科技信息，2009,21:49-50

ZHOU Q Q.Separation of Variables for Vibration Problems of Infinite and Semi-infinite Strings[J].China Science and Technology Information,2009,21:49-50

[6] 刘锐，李树生. 无界域上二阶非线性脉冲边值问题解的存在性[J]. 重庆工商大学学报(自然科学版)，2011,28(5):441-443

LIU R,LI S SH.Existence of Second-order Nonlinear Boundary Value Problem [J]. Journal of Chongqing Technology and business University(Natural Science Edition)，2011,28(5):441-443

责任编辑：田静

Discussion on the Vibration of Half Infinite Long String

LIU Yan

(School of Information Engineering, Lanzhou University of Finance and Economics, Lanzhou 730020, China)

Abstract：This paper discusses free vibration and forced vibration of half infinite long string, sets up string vibration equation on the basis of Newton Law and tries to solve the equation. The results show that the relation between the time and the vibration displacement of each particle under the forced vibration is much more complex, and that the vibration displacement is not only related to the vibration at the boundary point x=0 but also is directly related to force density.

Key words：string vibration equation; definite solution problem; d’Alembert formula; extension

中图分类号：O241

文献标志码：A

文章编号：1672-058X(2016)01-0047-05

作者简介：刘岩(1980-) ，女，河北定州人，讲师，硕士，从事凝聚态物理研究.

*基金项目：国家自然科学基金资助(61102002).

收稿日期：2015-08-06；修回日期：2015-09-06.

doi:10.16055/j.issn.1672-058X.2016.0001.011