讲活习题 提升能力

朱向阳



讲活习题提升能力

朱向阳

美国著名数学教育家波利亚指出，“掌握数学意味着什么呢？这就是善于解题，不仅善于解一些标准的题，还善于解一些要求独立思考、思路合理、见解独到和有发明创造的题”。解题是学生学习数学的必由之路，通过解题活动培养学生良好的思维能力，是数学教学的中心目标。教师在教学中，要善于利用习题，充分挖掘课本习题的思维训练功能，激发学生兴趣，开拓学生思路，培养学生的思维品质和应变能力。只有站在这样的高度，才能把习题吃透、讲活，使学生在巩固知识的同时培养思维能力。

一、一题多解，拓宽解题思路

学生在解题中常会出现一题多解。一题多解不仅可以充分提高学生综合运用知识解决问题的能力，锻炼思维的灵活性，还可以开拓学生的思路，帮助学生发现并掌握知识之间的联系，达到举一反三、融会贯通，培养思维的创造性。需要注意的是，一题多解并非单纯追求多解，重要的是针对不同目的，有的放矢。

1.多中立序，突出递进功能

面对一个新的数学问题，学生会依据已有知识和经验，从不同的方向和角度尝试解答。而教师则要针对出现的多种解法，在讲解时理清层次，循序渐进，推进学生数学能力的发展。

例1.教学北师大版教材一年级下册“两位数加减一位数不进位、不退位”这一内容，学生在解决“25+4=”时出现了以下不同的解法：

（1）数一数：从25开始往后数4个数，是29；

（2）画一画：在25根小棒基础上再画4根，是29根小棒（也可以是其他图形）；

（3）拨一拨：在计数器上先拨出25颗珠子，个位上再拨4颗珠子，是29；

（4）算一算：5+4=9，20+9=29。

这些解法，不仅是运用的知识方法不同、思考问题的角度不同，体现的思维层次和水平也不同。在解法交流时，教师要准确把握其层次性，从数一数、画一画到拨一拨，最后到列式算一算，促使学生的思维从具体到半抽象再到抽象的发展。

2.多中求质，突出基本解法

面对学生的多种解法，教师要善于抓住其中最基础、最本质的解法进行讲解，帮助学生透彻把握知识的本质。

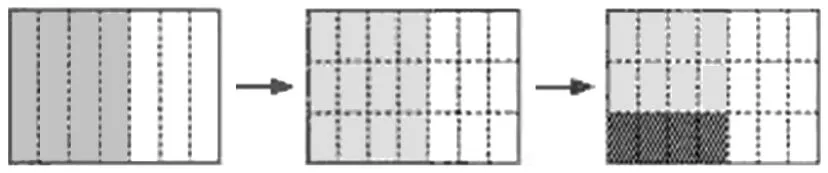
将几种方法进行比较，不难发现，学生依据除法运算的意义容易想到前两种方法，但方法（3）却是分数除法运算的一般方法。在解法交流时，教师要重点引导学生理解方法（3），帮助学生透彻把握分数除法的算理和算法。

3.多中求联，突出内在联系

同一个问题的多种解法之间往往并不是孤立的。沟通这些解法之间的联系，不仅有利于学生对问题的理解和方法的掌握，更有助于思维的完善和能力的提高。

例3.解决42×26这道题时，学生出现了以下一些方法：

接下来，教师让学生将这些解法进行分类。学生按横式、竖式、列表等形式将这些方法分为（1）（2）、（3）（4）、（5）（6）三类。在此基础上，教师引导学生按联系进行分类，发现其实（1）和（4）、（2）和（3）、（5）和（6）所体现的思路是一样的，只是形式有所区别；进一步观察，还发现在（5）和（6）中能找到（1）和（4）、（2）和（3）所对应的各部分。在比较和联系中，学生把握住这些方法的内在联系，从而完善自己的认知结构。

进行一题多解教学，能最大限度地调动学生已有的生活经验和认知基础，沟通多种解法之间的内在联系，抓住数学方法的本质，提高系统性，做到融会贯通，从而促进学生思维的发展。

二、一题多变，提高解题能力

解题的价值不在于答案本身，而在于弄清“是怎样想到这个解法的”“是什么促使你这样想或这样做的”。这就要求我们善于利用习题的变化，提高学生综合运用知识和方法的能力，培养良好的思维品质。

1.变单一为复合，提高综合性

有的习题涉及的知识单一，运用的方法简单，解决这样的习题，仅仅起到巩固知识的作用，对提高学生综合运用知识的能力、发展思维的作用有限。教师要善于对这些基本习题进行必要的改编。

例4.学了“数对”后，教材安排了如图1所示的练习，旨在考查学生是否会用数对确定位置。教师将它进行了改编：如图2，在长方形ABCD中，A点用数对表示为（1，5），C点用数对表示为（6，2），请你求出长方形的面积。

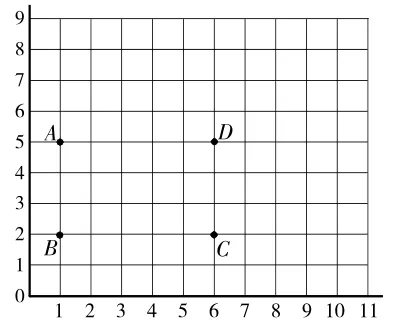
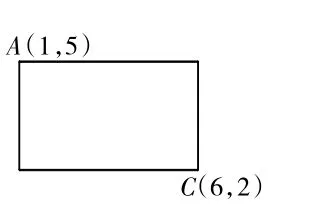
图2

不难发现，较之图1，图2的问题要求学生不仅要看懂数对、理解数对的意义，还要在不同数对相同项的比较中发现“差”就是长方形的长和宽，并运用长方形面积计算的方法得出结果。

剖析学生的解题过程，可以发现其分析问题的经历：这两个数对表示什么意义？跟长方形的长和宽有什么关系？如何找到长方形的长和宽？怎样求出长方形的面积？

提高习题的综合性，不仅仅是增加了知识的量，更重要的是学生的解题能力和思维品质都能在解题中得到提高。

2.变顺向为逆向，增强灵活性

我们都有这样的感受，顺走容易逆走难，解题也是如此。如果将习题中的已知条件和所求问题进行交换或改造，将顺向思维的习题改编成逆向思维的习题，适当增加解题的难度，对提高思维的灵活性和开放性大有裨益。

例5.“长方形的周长”这一内容中安排了这样一道习题：一个长方形的长是9cm，宽是4cm，它的周长是多少？

对已知条件和问题进行交换，可以得到下面的开放题：一个长方形的周长是26cm，它的长和宽各是多少？

如果原题中的问题是“它的面积是多少”，则可以得到这样的开放题：一个长方形的面积是36cm2，求它的长和宽。

上述两题的答案有无数个，为便于学生解答，可附加“它的长和宽都是整厘米数”这一条件。

若进一步加工，把长方形的长、宽、周长和面积都放在一道题里联系起来考虑，就可编出知识涉及面更宽的开放题：一个长方形的周长是26cm，它的长、宽各是多少？面积是多少？一个长方形的面积是36cm2，求它的长、宽和周长。

这两题还分别孕伏了最大值和最小值的知识：当长方形的周长一定，其面积具有最大值；当长方形的面积一定，其周长具有最小值。

一题多变的方式还有很多，重要的不在于变的形式，而在于变的目的和价值。只要教师注重知识方法的应用和学生思维品质的提高，解题就能成为培养学生思维能力的良好载体。

（作者单位：浙江省义乌市义亭小学）