分数的乘法和除法
2016-04-18胡重光
胡重光 周 志
分数的乘法和除法
胡重光周志

分数的加减法本文不作探讨,但需要指出一点:由于异分母分数的加减法可转化为同分母分数的加减法,而同分母分数的加减法只需将分子相加减,所以整数加减法的运算定律和性质都适合分数加减法。
一、分数乘法
分数乘法运算是小学数学的难点之一,教材分为分数乘整数、整数乘分数和分数乘分数三类分别教学。这一分法就表明,乘法是需要区分因数顺序的。从教材中的例题可知,分数乘整数表示若干个相同的分数相加,整数乘分数则表示求一个数的几分之几是多少,意义完全不同。
(一)分数乘整数
分数乘整数的教学过程如下图所示。

这里有一个矛盾:既然把分数乘整数与整数乘分数分开教学,就表明两者的意义是不相同的,但是上面的“男嘉宾”却说3个既可写成×3,又可写成3×。那么两者就没有区别了。
还有一个问题是,这里其实不需要画图分析。因为对六年级的学生来说,分数的加法无论是意义还是算法都已非常熟悉。不必要的重复不但浪费时间,而且影响学习兴趣。这个问题完全可以让学生独立解答,自己列式、自己计算,以提高他们独立思考和主动探索的能力。
(二)整数乘分数
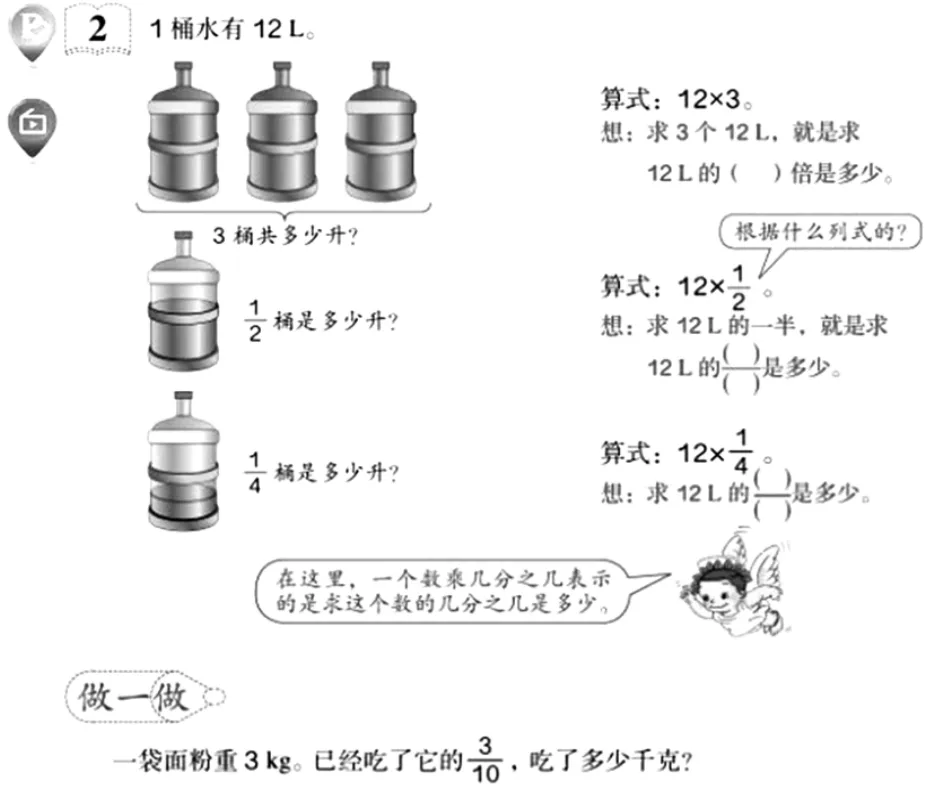
这里采用了类比的方法,先给出一个整数的例子,再将分数的情况与它作类比。但既然是类比,第二个“想”就应与第一个“想”结构相同,即应为:
但是纯粹从数学的角度教学,儿童是难以理解的,必须从儿童熟悉的实例出发。教材虽然举了实例,接下来却没有继续贯彻“现实数学”的原则。这时应该首先揭示问题的数量关系:水的总升数=每桶升数×桶数。
然后与学生讨论:如果桶数为分数怎样列式计算?最后得出,由于数量关系相同,不管是为整数还是为分数,都应用同样的算法,所以求桶的升数应该用每桶升数乘。
由此我们看到,抽象的数学与学生熟悉的现实问题相结合,就变得具体、亲切,容易接受了。紧密联系儿童的生活实际,是小学数学教学的一个法宝。
例如:火车每小时行驶120公里,照这样的速度,3小时行驶多少公里?小时行驶多少公里?
分析:根据“路程=速度×时间”的数量关系式,第一问的算式是:120×3,其意义是:求120的3倍是多少。
综上所述我们得到:整数乘分数,把这个整数与分子相乘作积的分子,分母不变。
这一法则与分数乘整数的法则相同。由此立即得出,乘法交换律对整数乘分数也成立。
以上的推导过程有两点值得注意,一是始终根据实际意义得出算法。这样做不但联系了生活实际,儿童感兴趣,而且道理表述清楚,儿童容易理解。二是先学习分子是1的情况,再学习分子不是1的情况,则后者的推导就很容易了。
(三)分数乘分数
这一部分内容的教学过程如下图所示。
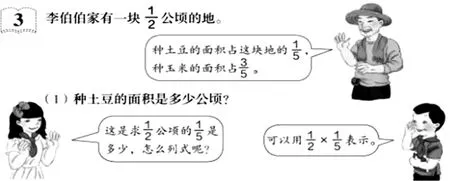

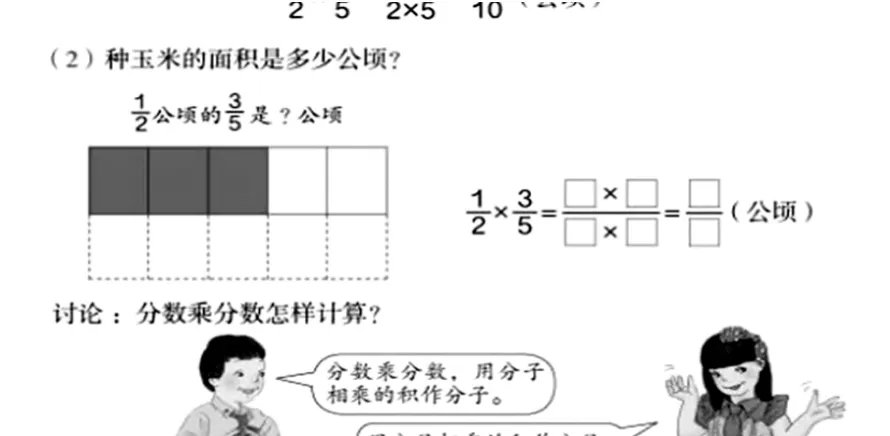
与整数乘分数的教学不同,这里用图详细地介绍了算理和算法,有理有据。但这一过程是相当繁琐的。实际上,分数乘分数的算理和算法都可以用实例很简单地得出。例如:拖拉机每小时耕地公顷,小时耕地多少公顷?
因为“耕地总面积=每小时耕地面积×耕地时间”,所以算式是:×,其意义是:求的是多少,因此算法是:先将平分成4份,再乘3,即:
这表明,两个分数相乘,只需将分子、分母分别相乘即可。由此我们得出:分数乘分数,把分母与分母相乘作积的分母,分子与分子相乘作积的分子。
这里利用了这样一个道理:将一个分数缩小(扩大)几倍,相当于将它的分母扩大(缩小)几倍。根据分数的意义,这是很明显的。类似地,将一个分数扩大(缩小)几倍,相当于将它的分母缩小(扩大)几倍。这两条性质很有用,我们完全可以在学习分数的基本性质时把它们作为推论提出来(当然不出现“推论”这一术语)。
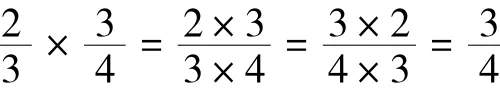
有了交换律和结合律,几个分数相乘就可以按任意的顺序进行,十分方便。
三、分数的除法
(一)分数除以整数
分数除以整数的教学与分数乘整数类似,过程如下图所示。
这类问题意义明确,算法简单,既然已要求学生“自己试着折一折,算一算”,教材再画图分析、详细推导,似乎就越俎代庖了。
由此我们得到:分数除以整数,可以用分数的分子除以整数的商作分子,分母不变。但是第二问÷3不能用这种方法,因为4不能被3整除。这时联想到前面一个数乘分数的意义或分数的性质可知也就是说:除以整数,等于乘这个整数的倒数。
二、整数除以分数和分数除以分数


这两类问题教材用同一个例子引入,教学过程如下图所示。这里应对“÷”写成“×”的道理进行细致的教学,不能简单地要求学生说出来。一个数除以分数比分数乘法更难理解,需要结合实例并与整数除法作类比。
分析:第一问的数量关系是:速度=路程÷时间,算式是:6÷2,其意义是:已知一个数的2倍是6,求这个数是多少。第二问的数量关系相同,算式应该是:÷,其意义是:已知一个数的(或倍)是,求这个数是多少。
于是我们得到:分数除以分数,等于乘这个分数的倒数。
综合前面分数除以整数的法则,我们得到:分数除以一个数,等于乘这个数的倒数。(本文是基金项目湖南省教育科学“十一五”规划课题(编号:XJK013 CGD051),“课程标准小学数学实验教材研究”、湖南省教育科学规划课题(编号:XJK013CJC004)、湖南省省级重点建设学科“课程与教学论”建设项目部分成果)
(作者单位:湖南第一师范学院长沙市实验小学)