求解更多极大T-传递内部的方法

杨晓晨,武彩萍,刘雪琴

(太原理工大学 数学学院,太原 030024)



求解更多极大T-传递内部的方法

杨晓晨,武彩萍,刘雪琴

(太原理工大学 数学学院,太原 030024)

摘要:在Fodor等给出的求解有限论域上极大T-传递内部构造方法的基础上,对求解一个模糊关系的更多极大T-传递内部的方法进行了讨论。首先,从任意行出发，对一个模糊关系的极大T-传递内部进行讨论;其次,从任意列出发对其进行了研究;最后,对与一个模糊关系最近的极大T-传递内部的求解方法进行了研究。

关键词:模糊关系;T-传递性;极大T-传递内部

模糊二元关系自Zadeh[1]提出以来,已被广泛应用于决策科学的诸多领域中,例如:聚类分析[2]、模糊量排序[3]、模糊选择函数[4]、模糊偏好结构[5]等。而在模糊关系的讨论中,传递性占据着相当重要的地位。1971年,Zadeh[6]提出了传递的概念,Ovchinnikov[7]又于1984年将它拓展为T-传递。

我们知道,从实际中获取的数据往往很难满足性质P,特别是在模糊情况下。因此,Bandler，et al[8]提出了模糊关系具有某种性质P的内部与闭包的概念。接下来的问题是用一个关系的内部或闭包代替原来不具有性质P的关系。然而,并不是所有模糊关系的内部与闭包都是存在的。例如,一个模糊关系的传递内部就不存在。1978年,Defays[9]提出了极大传递内部的概念,并给出了有限论域上任意模糊关系极大传递内部的构造方法。1994年, Fodor，et al[10]又给出了T为左连续t-模时,极大T-传递内部的求解方法。具体方法如下:保持已知模糊关系的第一行不变,在第一行的基础上构造第二行,又通过第一行和第二行构造第三行,依次进行下去,即可得到该关系的极大T-传递内部。2010年,韩和王[11]又从最后一行出发得到已知关系不同的极大T-传递内部。

基于上述构造方法,我们从任意行或列出发寻找已知关系的极大T-传递内部,并通过一个例子加以说明。由于一个模糊关系的极大T-传递内部不是唯一的,我们还试图寻找与已知关系距离最近的极大T-传递内部。

1预备知识

本节我们给出了t-模、模糊蕴涵以及模糊关系T-传递性的相关定义与结论。

定义1.1[12]设，T:[0,1]×[0,1]→[0,1],若T满足:

1) 对称性:∀x,y∈[0,1],

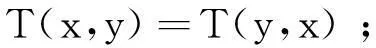
2) 单调性:∀x1≤x2,y1≤y2,

3) 结合律:∀x,y,z∈[0,1],

4) 边界条件:∀x∈[0,1],T(1,x)=x,则称T为一个t-模。例如:T(x,y)=min(x,y)为一个t-模,我们称之为取小t-模。T(x,y)=max(x+y-1,0)为一个t-模,我们称它为Lukasiewiczt-模,记作W.

定义1.2[10]设，R为A上的模糊关系,T是一个t-模。若R满足:∀a,b,c∈A,T(R(a,c),R(c,b))≤R(a,b),则称R是T-传递的。

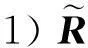
定义1.4[7]设,I:[0,1]×[0,1]→[0,1],若I(x,y)对x单减,对y单增,且满足:I(1,0)=0,I(0,0)=I(1,1)=1,则称I为一个模糊蕴涵,简称蕴涵。

2极大T-传递内部求解的方法

首先介绍Fodor[10]等给出的求解有限论域上模糊关系的极大T-传递内部的构造方法。设有限论域A={a1,a2,…,an},R是A上的一个模糊关系,T是一个左连续t-模。

第一步:定义∀a∈A,

其中

下面我们从R的任意行或列出发,构造R的不同的极大T-传递内部。文中,设有限论域A={a1,a2,…,an},R是A上的一个模糊关系,记作n×n矩阵。T是一个左连续t-模。

2.1从任意行出发构造R的极大T-传递内部

定理2.1若R是A上的一个T-传递关系,R′是通过交换R的第l行与第m行,同时交换R的第l列与第m列得到的,则R′也是一个T-传递关系。

证明因为R是A上的一个T-传递关系,则∀i,j,k,(1≤i,j,k≤n)有:

现交换R的第l行与第m行,得到:

再交换R1的第l列与第m列,得到:

综合,即得:

下证R′是一个T-传递关系,即对∀i,j,k,(1≤i,j,k≤n)有:

(Ⅰ)

以下分9种情况进行讨论。

1) 当i,j≠l,m时。

若k≠l,m,则

若k=l,则

若k=m,则

故，T(R′(ai,ak),R′(ak,aj))≤R′(ai,aj) .

2) 当i≠l,m,j=l时。

若k≠l,m,则

若k=l,则

若k=m,则

故，T(R′(ai,ak),R′(ak,aj))≤R′(ai,aj).

3) 当i≠l,m,j=m时。

若k≠l,m,则

若k=l,则

若k=m,则

故,T(R′(ai,ak),R′(ak,aj))≤R′(ai,aj).

4) 当i=l,j≠l,m时。

若k≠l,m,则

若k=l,则

若k=m,则

故,T(R′(ai,ak),R′(ak,aj))≤R′(ai,aj) .

5) 当i=m,j≠l,m时。

若k≠l,m,则

若k=l,则

若k=m,则

故,T(R′(ai,ak),R′(ak,aj))≤R′(ai,aj).

6) 当i=l,j=m时。

若k≠l,m,则

若k=l,则

若k=m,则

故,T(R′(ai,ak),R′(ak,aj))≤R′(ai,aj).

7) 当i=m,j=l时。

若k≠l,m,则

若k=l,则

若k=m,则

故,T(R′(ai,ak),R′(ak,aj))≤R′(ai,aj).

8) 当i,j=l时。

若k≠l,m,则

若k=l,则

若k=m,则

故,T(R′(ai,ak),R′(ak,aj))≤R′(ai,aj).

9) 当i,j=m时。

若k≠l,m,则

若k=l,则

若k=m, 则

故,T(R′(ai,ak),R′(ak,aj))≤R′(ai,aj).

综上,(Ⅰ)成立。因此,R′是一个T-传递关系。

1) 若i,j≠l且i,j≠m,则

2) 若i≠l,m且j=l,则

3) 若i≠l,m且j=m,则

4) 若i=l且j≠l,m,则

5) 若i=m且j≠l,m,则

6) 若i=l且j=m,则

7) 若i=m且j=l,则

8) 若i=j=l,则

9) 若i=j=m,则

2.2从任意列出发构造R的极大T-传递内部

本节我们先从R的第一列出发构造R的极大T-传递内部。

定理2.3若R是A上的一个T-传递关系,RT也是一个T-传递关系。

证明由R是A上的一个T-传递关系,则对∀i,j,k,(1≤i,j,k≤n)有:

又因为

因此,T(RT(ai,ak),RT(ak,aj))≤RT(ai,aj),即RT是一个T-传递关系。

下面我们从任意列出发求解一个模糊关系的极大T-传递内部。

证明由定理2.2、定理2.3及定理2.4立得。

2.3举例

在下面的例子中,若将R的第i行作为第一行,第j行作为第二行,第k行作为第三行,同时将第i列作为第一列,第j列作为第二列,第k列作为第三列,则将得到的关系记作Rijk.

例1设A={a,b,c},定义R如下:

令T(x,y)=W(x,y)=max(x+y-1,0),IW(x,y)=min(1-x+y,1).显然,R不是一个T-传递关系。现在我们根据上述方法求解R的极大T-传递内部。

方法1：从任意行出发求解R的极大T-传递内部。由Fodor等的方法得到的极大T-传递内部:

与由R123得到的极大T-传递内部相同。

令R的第一行为第一行,第二行为第三行,第三行为第二行,同时将R的第一列为第一列,第二列为第三列,第三列为第二列,即交换R的第二行和第三行,第二列和第三列,得到:

求得R132的极大T-传递内部:

类似的,由R213,R231,R312,R321求得R的极大T-传递内部分别为:

方法2：从任意列出发求解R的极大T-传递内部。

首先,求R123的转置,即求R的转置为:

然后,求得RT的极大T-传递内部为:

因此,求得R的极大T-传递内部:

类似的,由(R132)T,(R213)T,(R231)T,(R312)T,(R321)T,求得R的极大T-传递内部分别为:

3与R距离最近的极大T-传递内部

一般的,一个模糊关系的极大T-传递内部是不唯一的。在实际应用中,我们常需求得与该模糊关系最近的极大T-传递内部。下面我们给出与R最近的极大T-传递内部的求解方法。

证明定义R1(ai,aj)如下:

下面分5种情况进行讨论。

1) 若i≠j≠k,则

2) 若i≠j且i=k,则

3) 若i≠j且j=k,则

4) 若i=j=k,则

5) 若i=j且i,j≠k,则

总之,对任意i,j,k有：

下面将详细讨论距该关系海明距离最近的极大T-传递内部。

根据海明距离，

注:R的极大T-传递内部不一定距R最近。

下面给出距R最近的极大T-传递内部的求解方法。具体步骤如下:

第一步:定义

第二步:求解下列规划问题:

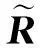
(Ⅱ)

由定理3.1及(Ⅱ)可得:

解得:

y=3.4,

故与R距离最近的极大T-传递内部:

且最小距离为:

4结论

我们给出了求解一个模糊关系更多极大T-传递内部的方法。现对本文的结论进行概括总结,并与文献[10-11]中的结果进行对比。

首先,Fodor等和韩等分别从第一行与最后一行出发构造R的极大T-传递内部。然而, 我们从R的任意行或任意列出发,求得更多的极大T-传递内部。

其次,通过对极大T-传递内部特征的研究,给出了求解距一个模糊关系最近的极大T-传递内部的求解方法。鉴于计算过程的复杂性,尤其是当n较大时,我们通过计算机编程实现这些求解方法,将进一步延伸T-传递在计算机科学领域的应用。

参考文献：

[1]ZADEH L A.Fuzzy sets[J].Information and Control,1965,8:338-353.

[2]WANG X Z,RUAN D,KERRE E.Mathematics of fuzziness-basic issues[M].Berlin:Springer-Verlag,2007.

[3]WANG X Z,KERRE E.Reasonable properties for the ordering of fuzzy quantities：Ⅱ[J].Fuzzy Sets and Systems,2001,118:387-405.

[4]GEORGESCU I.Fuzzy choice functions[M].Berlin:Springer-Verlag,2007.

[6]ZADEH L A.Similarity relations and fuzzy ordering[J].Information Sciences,1971,33:177-220.

[7]OVCHINNIKOV S.Representations of transitive fuzzy relations[C].Skala H J,Termini S，Tvillas E.Aspects of vagueness.Reidel.Dordrecht-Boston,1984：105-118.

[8]BANDLER W,KOHOUT L J.Special properties, closures and interiors of crisp and fuzzy relations[J].Fuzzy Sets and Systems,1988,26:317-331.

[9]DEFAYS M.Analyse hiérarchique des préfrences et généralisations de la transitivit？[J].Math Sci Hum,1978,16:5-27.

[10]FODORJC,ROUBENSM.Fuzzypreferencemodellingandmulticriteriadecisionsupport[M].Dordrecht:KluwerAcademicPublishers,1994.

[11]韩红娟,王绪柱.求极大T-传递内部的新方法[J].模糊系统与数学,2010,24:92-97.

[12]KLEMENTE,MESIARR,PAPE.Triangularnorms[M].Dordrecht,Boston,London:KluwerAcademicPublishers,2000.

[13]FODORJC,ROUBENSM.Structureoftransitivevaluedbinaryrelation[J].MathematicalSocialSciences,1995,30:71-94.

(编辑：朱倩)

A Method to Find More MaximalT-Transitive Interiors

YANG Xiaochen,WU Caiping,LIU Xueqin

(CollegeofMathematics,TaiyuanUniversityofTechnology,Taiyuan030024,China)

Abstract:On the basis of the constructive approach of finding a maximal T-transitive interior of a fuzzy relation on a finite universe proposed by Fodor et al,we suggest a method to find more maximal T-transitive interiors. First,we construct different maximal T-transitive interiors from any rows. Then,we find different interiors from any columns. Finally,we present a method to find the maximal T-transitive interior that is the closest to the original fuzzy relation.

Key words:fuzzy relation;T-transitivity;maximal T-transitive interior

中图分类号:O159

文献标识码:A

DOI：10.16355/j.cnki.issn1007-9432tyut.2016.01.023

作者简介：杨晓晨(1991-),女,山西灵石人,硕士生,主要从事模糊决策研究,(E-mail)tyyangxiaochen@sohu.com通讯作者：武彩萍,女,副教授,硕导,主要从事模糊决策的研究，(E-mail)wucaiping2010@163.com

基金项目：国家自然科学基金青年基金资助项目:基于模糊信息粒化方法的耦合性多灾种综合风险评估模型的研究(41101507);山西省自然科学基金资助项目(2013011004-1);山西省研究生教育改革研究课题(20142028)

收稿日期：2015-04-21

文章编号:1007-9432(2016)01-0120-07