非对称弹道四终端纳米结构中的热整流性质研究

冯　卉,杨　平,郭　玮,朱思宇,张文星

(太原理工大学 物理与光电工程学院,太原 030024)



非对称弹道四终端纳米结构中的热整流性质研究

冯卉,杨平,郭玮,朱思宇,张文星

(太原理工大学 物理与光电工程学院,太原 030024)

摘要:对非对称弹道四终端纳米结构中的热整流性质进行了研究。研究结果发现，导致该结构出现热整流现象的两个必要因素是能量输入端与能量输出端应具有不等的横向声子模密度;除了与输入端和输出端连接的热源以外,还需有与该结构连接的其他附加热源的存在；只有这两个因素共同作用才能产生热整流行为,任何一个因素都不能单独引发弹道系统的热整流现象。

关键词:热整流;非对称;弹道;四终端纳米结构;声子模密度

如何控制热流、消除热的不良影响及合理利用热能当属国际上广泛关注的研究方向。为实现上述目标就需要充分了解介观/纳观量子系统中热流的非线性输运性质,譬如热整流行为或热不对称性,即在保持连接纳米结构两终端热源温差不变的情况下,调换两端的热源,会发现沿正反两方向热流不相等的现象。到目前为止,关于两终端纳米结构[1-3]、三终端纳米结构[4-6]、碳纳米管[7]以及石墨烯纳米带[8]中的热整流现象的理论研究已先后被完成。与此同时,一个重要的实验观察到了纳米管中的热整流行为[9],并且这个实验结果又被在一个质量不对称的纳米管中通过非平衡态分子动力学方法成功复制[10]。以上的研究结果表明,导致热整流行为的关键因素是低维纳米结构中的相互作用势或材料的质量或材料的形状具有不对称性。最近,有研究者通过一个具有不同热接触尺寸的金字塔结构并利用非平衡态分子动力学方法对三维非对称纳米结构的热整流性质进行了研究[11]。然而,研究结果却表明,以前关于纳米结构形状的不对称性单独引发热整流行为的结论是不完整的。因此,考虑多种不同因素对热整流性质的研究是必不可少的。

尽管在研究电子输运及微电子设置(包括电二极管和电整流器[12-14])方面普遍使用两终端结构,但三终端和四终端结构仍可呈现出更多的物理新现象,譬如三终端或更多终端结构在能量输运过程中其它终端(非能量输入、输出终端)可被用作控制端,起到调控结构中能量传输的作用[15-17]。随着纳米实验技术的迅速发展,在过去的10年里已经完成了对各种纳观系统及两终端[18-26]、三终端[27-28]以及四终端纳米结构[29]中的介观热输运性质的研究。结果显示,多终端结构比两终端结构能够展示出更多有趣的物理性质。

本文研究了低温下非对称弹道四终端电介质纳米结构(DABFTS)中的热整流性质。根据有关介观弹道声子输运的研究[18-29],展示了非对称弹道四终端电介质纳米结构中的热整流行为、声子输运的非线性特性,并阐述了产生热整流的机制,提出了非对称弹道四终端电介质纳米结构中产生热整流的两个必要因素，能量输入端与能量输出端应具有不等的横向声子模密度;除了具有连接热源的输入端和输出端以外,还需有连接其它热源的终端。此外,还具体讨论了这两个必要因素是如何导致非对称弹道四终端电介质纳米结构中产生热整流的物理机理。由此得到一个关于弹道系统中热整流的新观点,即热整流现象不是由单一的非对称性因素导致的,而是由多个因素共同导致的。

1模型与方法

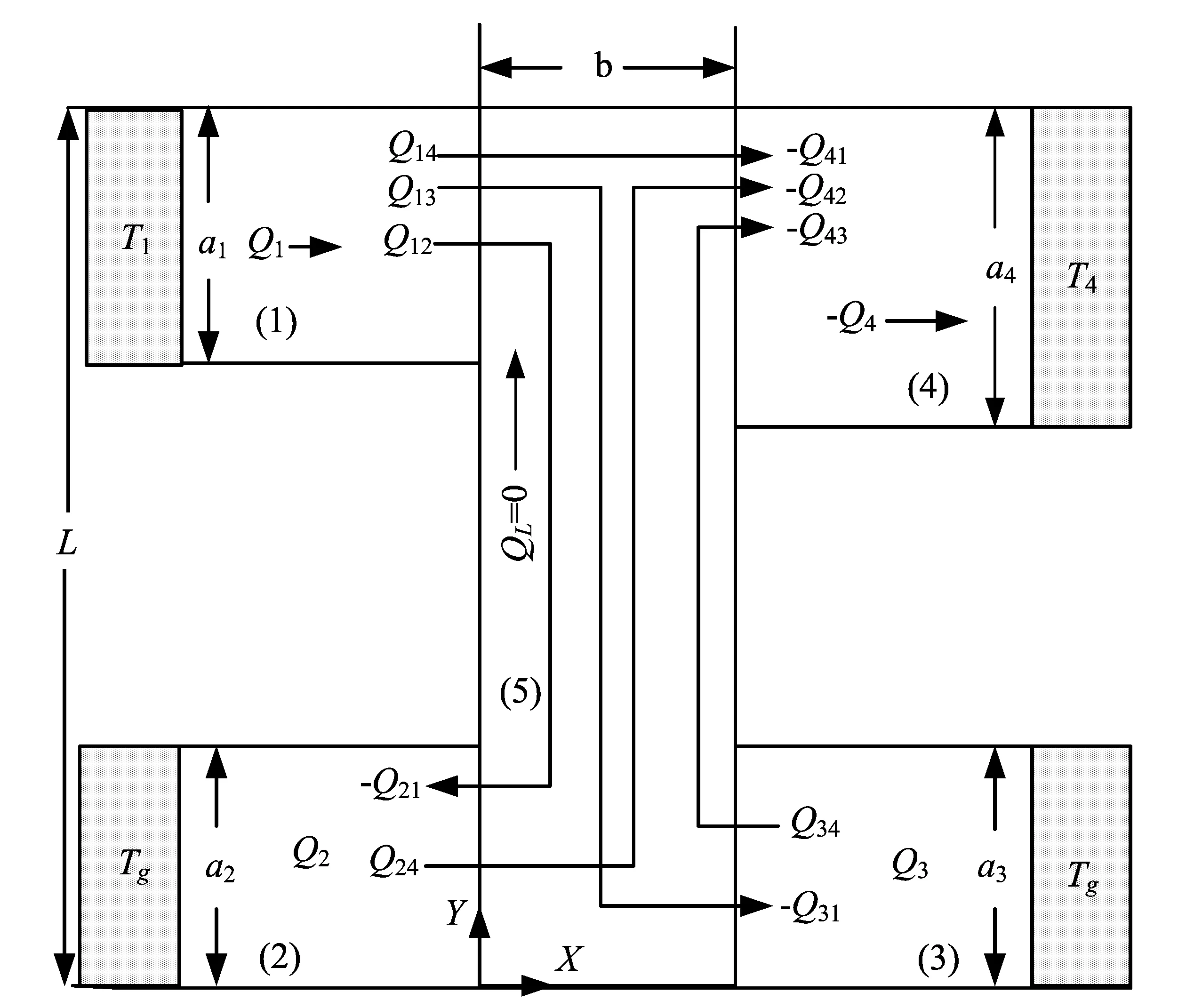
图1　非对称弹道四终端电介质纳米结构示意图Fig.1　Schematic illustration of a dielectric asymmetricfour-terminal ballistic junction structure (DABFTS)

图1是一个二维非对称弹道四终端电介质纳米结构,由1个矩形散射区和4条纳米线组成,其中的4条纳米线分别与4个热源连接。在低温情况下,由于声子的平均自由程大于系统尺寸,因此只有在纳米线与矩形散射区的连接处发生声子散射,声子在纳米线和矩形散射区的内部隶属于弹道输运。因此,这个非对称弹道四终端电介质纳米结构可以看做是一个弹道系统。根据Landauer和Buttiker的关于输运的理论构架,第i个终端(第i个纳米线)中的净热流Qi的表达式为[29]:

(1)

为了研究非对称弹道四终端电介质纳米结构中的热整流行为,将终端1作为热能输入端,终端4作为热能输出端,分别与热源1和热源4连接,而且假设热源1和热源4的温度有如下关系:T1≥T4。热源2和热源3分别与两个温度相等的热源连接,即T2=T3。由式(1)可以清楚地看到,终端1或终端4的热流是一个关于热源2和热源3的温度的函数,相应温度T2和T3可以看做是阀门温度:Tg=T2=T3,阀门温度T2和T3能够影响终端1和终端4的热流。

当系统达到稳定状态时,让沿矩形区域5内垂直方向的净热流QL为零,由图1可得:

(2)

由式(1)可得:

式(2)说明从终端1流向终端2和终端3的热流等于从终端2和终端3流向终端4的热流。如图1所示,在整个热流的流动过程中,热能在终端2和终端3保持守恒,终端2和终端3相当于一个能量转换器,这意味着终端1的热能能够毫无损失的传输到终端4。很明显地,式(2)中的温度T2和T3必须满足如下关系:T1≥T2=T3≥T4。根据式(1),将式(2)改写为

(3)

是单位阶梯函数。与式(2)不同的是,式(3)中的每一项都是只关于单一热源温度的函数,而且式(3)可以写为

(4)

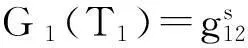
2结果与讨论

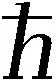
图中结构的几何参数a1=a2=a3=20 nm；a4=40 nm；b=20 nm；L=100 nm；v=5 000 ms-1图2　热流Qsd随温度ΔT14变化情况示意图Fig.2　Thermal flow Qsd vs temperature ΔT14

图3　非对称弹道四终端电介质纳米结构的终端1、矩形区域5以及终端4内的离散横向声子模的截止频率示意图Fig.3　Schematic illustration of the cutoff frequencies of discrete transverse phonon modes (straight lines) forterminal 1,rectangle region 5,and terminal 4 in the DABFTS

2.1正方温差的声子模

根据终端1的

2.2反方温差的声子模

2.3热整流

(5)

(6)

如图2所示,由于式(5)和式(6)中的第一项比第二项和第三项大至少一个数量级,所以保留第一项,忽略第二项和第三项。式(5)和式(6)的近似形式可以表示为

(7)

(8)

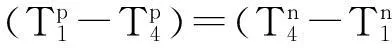
图4　热流 随温度T的变化情况示意图Fig.4　Thermal flow vs temperature T

2.4热整流的两个必要因素

为了进一步探究引起热整流的原因,交换一下非对称弹道四终端电介质纳米结构中终端3与终端4的横向尺寸,用a1=a2=a4=20nm,a3=40nm代替a1=a2=a3=20nm,a4=40nm。在改变后的非对称弹道四终端电介质纳米结构中,终端1和终端4具有相等的横向尺寸,终端2和终端3具有不等的横向尺寸,所以改变后的非对称弹道四终端电介质纳米结构仍是非对称的。如图5所示,当Tg=15K时,Qsd随ΔT14的变化曲线在改变后的结构中是对称的,与在改变前的结构中是非对称的结果不同。通过比较以上结果总结出非对称弹道四终端电介质纳米结构发生热整流行为的一个必要因素是:终端1和终端4应具有不等的横向声子模密度。此外,热源2和热源3的存在是该结构发生热整流行为的另一个必要因素。如果移除此结构中的热源2和热源3或终端2和终端3,此结构将变成具有两个热源的T型弹道结构[28],那么即使终端1和终端

4具有不等的横向声子模密度,也不会出现热整流行为。换句话说,热源2和热源3为产生热整流创造了一个有效环境,同时,终端1和终端4的不等横向声子模密度导致了非对称弹道四终端电介质纳米结构的热整流行为。

图5　Tg=15K时,Qsd随ΔT14的变化曲线Fig.5　Thermal flow Qsd vs ΔT14for Tg=15 K

3结束语

展示了非对称弹道四终端电介质纳米结构中的热整流行为,通过分析横向声子模中声子输运的非线性特性解释了热整流的机制。能量输入端(终端1)和能量输出端(终端4)间的不等横向声子模密度导致非对称弹道四终端电介质纳米结构中产生热整流,该不等横向声子模密度使得相关温度对(T1,T4)在正、反方温差两种情况下分别处于不同的温度范围。在正方温差情况下,相关温度对(T1,T4)处于能够输运较多热能的高温范围;相反地,在反方温差情况下,相关温度对(T1,T4)处于能够输运较少热能的低温范围。因此,能量输入端和能量输出端之间的不等横向声子模密度是非对称弹道四终端电介质纳米结构中产生热整流的一个必要因素,但它不是唯一因素。就像上面讨论的,该纳米结构中产生热整流的另一个必要因素是除了具有连接热源的输入端和输出端以外,还具有连接其它热源的终端。更重要的是,只有这两个因素共同作用才能导致热整流行为,其中的任何一个都不能单独引发弹道系统的热整流行为。

参考文献：

[1]TERRANEO M,PEYRARD M,CASATI G.Controlling the energy flow in nonlinear lattices:a model for a thermal rectifier[J].Phys Rev Lett,2002,88(9):094302(1)-094302(5).

[2]LI B,WANG L,CASATI G.Thermal diode:rectification of heat flux[J].Phys Rev Lett,2004,93(18):184301-184301.

[3]YANG N,LI N,WANG L.Thermal rectification and negative differential thermal resistance in lattices with mass gradient[J].Phys Rev B,2007,76(2):020301-020301.

[4]MING Y,WANG Z X,DING Z J.Ballistic thermal rectification in asymmetric three-terminal mesoscopic dielectric systems[J].New J Phys,2010,12(10):103041-103041.

[5]WU L A,SEGAL D.Sufficient conditions for thermal rectification in hybrid quantum structures[J].Phys Rev Lett,2009,102(9):095503-095503.

[6]ZHANG L,WANG J S,LI B.Ballistic thermal rectification in nanoscale three-terminal junctions[J].Phys Rev B,2010,81(10):100301-100301.

[7]WU G,LI B.Thermal rectification in carbon nanotube intramolecular junctions:Molecular dynamics calculations[J].Phys Rev B,2007,76(8):085424(1)-085424(8).

[8]HU J,RUAN X,CHEN Y P.Thermal conductivity and thermal rectification in graphene nanoribbons:a molecular dynamics study[J].Nano Lett,2009,9(7):2730(1)-2730(13).

[9]CHANG C W,OKAWA D,MAJUMDAR A.Solid-State thermal rectifier[J].Science,2006,314(5):1121-1124.

[10]ALAGHEMANDI M,LORY F,ALGARLGAR E.Nanotechnology,2010,21(7):075704.

[11]LEE J,VARSHNEY V,ROY A K.Thermal rectification in three-dimensional asymmetric nanostructure[J].Nano Lett,2012,12(7):3491-3496.

[12]BÜTTIKER M.Four-terminal phase-coherent conductance[J].Phys Rev Lett,1986,57(14):1761-1764.

[13]WU H,SPRUNG D W L,MARTORELL J.Quantum wire with periodic serial structure[J].Phys Rev B,1991,44(12):6351-6360.

[14]WANG J,WANG Y J,GUO H.Ballistic-electron transport through a coupled-quantum-wire system[J].Phys Rev B,1992,46(4):2420-2427.

[15]SOLS F,MACUCCI M,RAVAIOLI U.On the possibility of transistor action based on quantum interference phenomena[J].Appl Phys Lett,1988,54(4):350-352.

[16]ANDRIOTIS A N,MENON M,SRIVASTAVA D.Ballistic switching and rectification in single wall carbon nanotube Y junctions[J].Appl Phys Lett,2001,79(2):266-268.

[17]WORSCHECH L,XU H Q,FORCHEI A.Bias-voltage-induced asymmetry in nanoelectronic Y-branches[J].Appl Phys Lett,2001,79(2):3287-3289.

[18]CAHILL D G,FORD W K,GOODSON K E.Nanoscale thermal transport [J].J Appl Phys,2003,93(2):793-818.

[19]REGO L G C,KIRCZENOW G.Quantized termal conductance of dielectric quantum wires[J].Phys Rev Lett,1998,81(1):232-235.

[20]SCHWAB K,HENRIKSEN E A,WORLOCK J M.Measurement of the quantum of thermal conductance[J].Nature (London),2000,404(10):974-977.

[21]GLAVIN B A.Low-temperature heat transfer in nanowires[J].Phys Rev Lett,2001,86(19):4318-4321.

[22]YAMAMOTO T,WATANABE K.Nonequilibrium green’s function approach to phonon transport in defective carbon nnotubes[J].Phys Rev Lett,2006,96(25):255503(1)-255503(4).

[23]WANG J,WANG J S.Mode-dependent energy transmission across nanotube junctions calculated with a lattice dynamics approach[J].Phys Rev B,2006,74(5):054303(1)-054303(5).

[24]ANGELESCU D E,CROSS M C.Roukes M L.Heat transport in mesoscopic systems[J].Superlattices and Microstructures,1998,23(3):673(1)-673(22).

[25]BLENCOWE M P.Quantum energy flow in mesoscopic dielectric structures[J].Phys Rev B,1999,59(7):4992-4998.

[26]SANTAMORE D H,CROSS M C.Effect of surface roughness on the universal thermal conductance[J].Phys Rev B,2001,63(18):184306(1)-184306(6).

[27]MING Y,WANGA Z X,LI Q.Nonlinear thermal properties of three-terminal mesoscopic dielectric systems[J].Appl Phys Lett,2007,91(14):143508(1)-143508(9).

[28]YANG P,SUN Q F,GUO H.Thermal transport in a dielectric T-shaped quantum wire[J].Phys Rev B,2007,75(23):235319(1)-235319(6).

[29]SUN Q F,YANG P,GUO H.Four-terminal thermal conductance of mesoscopic dielectric systems[J].Phys Rev Lett,2002,89(17):175901(1)-175901(4).

(编辑：刘笑达)

Thermal Rectification in an Asymmetric Ballistic Four-terminal Nanostructure

FENG Hui,YANG Ping,GUO Wei,ZHU Siyu,ZHANG Wenxing

(CollegeofPhysicsandOptoelectronics,TaiyuanUniversityofTechnology,Taiyuan030024,China)

Abstract:Thermal rectification is studied theoretically in an asymmetric ballistic four-terminal nanostructure.Different from previous studies,we find two necessary factors that cause thermal rectification in the structure:1) the existence of the unequal density transverse phonon modes among energy input terminal and energy output terminal,2) the existence of thermal reservoirs connected to the other two terminals.Only the combination of two necessary factors can bring about thermal rectification; a single factor is not enough to induce thermal rectifying behavior independently.

Key words:thermal rectification;asymmetric;ballistic;four-terminal nanostructure;density phonon modes

中图分类号:O469

文献标识码:A

DOI：10.16355/j.cnki.issn1007-9432tyut.2016.01.022

作者简介：冯卉(1989-)，女，山东临沂人，硕士生，主要从事凝聚态物理研究，(E-mail)meety89@163.com通讯作者：杨平，博士，副教授，主要从事凝聚态物理研究-介观输运研究，(E-mail)yangping01@tyut.edu.cn

基金项目：国家自然科学基金资助项目:单分子磁体的输运电流噪声特性研究(11204203)

收稿日期：2015-04-15

文章编号:1007-9432(2016)01-0113-07