轴向压缩下泡沫铝填充薄壁圆管吸能特性研究

黄　睿,刘志芳,路国运,闫庆荣

(太原理工大学 应用力学与生物医学工程研究所,太原 030024)



轴向压缩下泡沫铝填充薄壁圆管吸能特性研究

黄睿,刘志芳,路国运,闫庆荣

(太原理工大学 应用力学与生物医学工程研究所,太原 030024)

摘要:利用有限元软件ABAQUS对7种不同几何尺寸的泡沫铝填充管进行准静态轴向压缩的数值仿真分析,系统地研究了管的高度、壁厚、直径以及泡沫铝的填充对圆管吸能性能的影响；与实验对比，分析了7种泡沫铝填充试件的平均载荷、初始峰值载荷、比吸能(ESA)和压缩力效率(ECF)等吸能评价指标。研究结果表明,泡沫铝填充管在准静态轴向压缩时,管的壁厚与直径对管的吸能性能有显著影响;管的高度对其吸能性能影响较小,但高度的增加可以增加管的总吸能;泡沫铝的填充提高了管的承载力、总吸能、比吸能和压缩力效率。本研究成果可为设计理想的缓冲吸能装置提供一定的技术依据。

关键词:泡沫铝填充管;轴向压缩;能量吸收;数值模拟

薄壁金属管是工程结构中常用的一种构件,也是一种理想的缓冲吸能元件。因其结构简单、易于加工、具有良好的能量吸收特性,而广泛应用于航空航天、交通运输、石油化工等领域。但是，薄壁金属单管结构的承载力较弱,且变形不稳定,容易发生欧拉失稳。因此，为了提高管件的吸能效率,泡沫填充管作为一种新型的缓冲吸能元件被广泛地应用于飞行器设计、汽车耐撞性等领域。泡沫金属是一种轻质高效的材料,它有着几乎不变的平应力,而且压缩行程较长,具有较高的吸能效率,将其填充到薄壁金属管中，可构成一种性能良好的抗冲击吸能装置,具有广阔的应用前景。因而对泡沫金属填充薄壁管状结构的研究具有十分重要的意义。

近年来,国内外学者对于薄壁金属管及其泡沫填充结构的吸能特性做了大量的研究,并取得了一些研究成果。早期ANDREWS，et al[1]，GUILLOW,et al[2]通过大量的实验,观察薄壁金属圆管的轴向压溃变形,发现变形模式的不同主要与管件的长度与直径比值L/D以及直径与厚度的比值D/d有关；CHEN,et al[3]通过有限元模拟法预测了轴向冲击下圆管的初始峰值载荷，讨论了影响初始峰值载荷大小的因素，如管的几何尺寸、材料的属性和冲击速度等；KARAGIOZOVA,et al[4]研究了圆管结构的几何尺寸、材料参数以及边界条件对结构的屈曲变形模式和吸能的影响；SEITZBERGER,et al[5]对泡沫填充管的轴向压缩特性分别进行了实验和数值模拟研究,发现填充泡沫对圆管吸能性能的提高有很大的作用；桂良进等[6-7]对轴向压缩及轴向冲击下泡沫填充管的吸能特性进行了研究,系统地分析了结构的几何尺寸、材料参数、加载速率对吸能的影响，并对结构进行了优化设计；SANTOSA,et al[8]通过实验和数值模拟的方法对轴向压缩下的泡沫铝填充管的力学响应进行了研究,在模拟中用动态显式分析法模拟准静态实验,所预测出的变形模式以及压溃力，与实验得到的结果吻合较好。基于在高速列车上的应用,张志新[9]设计了管长度不同的泡沫铝填充装置，并将它带入到列车模型中,通过数值模拟分析发现，该装置对保护乘客安全起到很大的作用。

综上所述,前人的研究都只单独考虑几何尺寸或是填充泡沫对薄壁金属管吸能性能的影响。在此基础上,笔者同时考虑管的几何尺寸的改变和泡沫铝填充效果对薄壁金属管吸能性能的影响。首先通过轴向压缩实验给出了两组试件的变形模态图与载荷-位移曲线,利用ABAQUS软件建立了与实验对应的有限元模型,并与实验进行对比,验证了有限元模型的可靠性与有效性；之后利用初始峰值载荷、平均载荷、比吸能、压缩率等吸能评价指标系统地分析了圆管的壁厚、高度、直径和泡沫铝的填充对其能量吸收的影响。

1数值模拟

为研究准静态轴向载荷作用下泡沫铝填充薄壁金属管的吸能性能,制备了7种不同几何尺寸的泡沫铝填充薄壁金属圆管与空圆管。其中，金属外管的高度为h=30,45,60 mm；壁厚为d=0.9,1.2,1.5 mm；外径为D=30,35,40 mm。针对不同的薄壁金属外管,内部填充泡沫铝的高度与金属圆管相同,直径为薄壁金属圆管的内径。

1.1有限元模型

利用有限元软件ABAQUS/Explicit，对泡沫铝填充薄壁金属圆管在准静态轴向载荷作用下的吸能性能进行了数值模拟,并与空管进行了对比。有限元模型主要由上端刚性板、中间泡沫铝填充圆管结构或圆管、下端刚性板3部分组成。圆管或者泡沫铝填充管放置在下端刚性板的中间,上端刚性板向下移动实现对管结构的准静态轴向加载。下端的刚性板约束了全部6个自由度,而上端刚性板约束了除Z轴方向的平动自由度以外的其他自由度。

圆管采用4节点壳单元(S4R),沿厚度方向设置5个积分点。泡沫铝采用8节点六面体实体单元(C3D8R)。上、下的刚性板为离散刚体模型,采用六面体网格划分。圆管与泡沫铝之间,圆管与上、下刚板之间,以及圆管自身在压缩过程中的接触采用通用接触，接触面间的摩擦系数为0.2。

1.2有限元模型的可靠性验证

为了验证建立的有限元模型的有效性与计算的可靠性,与实验结果进行了比较。实验使用的薄壁金属圆管材料为铝合金AA6061-T6,弹性模量E=68.2 GPa,泊松比μ=0.33,密度ρ=2.7 mg/mm3,材料的应力-应变曲线如图1所示。作为填充材料的泡沫铝,密度ρ=0.33 mg/mm3,弹性模量E=80 MPa,泊松比μ=0.01,泡沫铝材料的应力-应变曲线如图2所示,其平台应力σp=3.6 MPa。实验中泡沫铝填充物自由放入圆管内,其柱面与管内壁不做任何粘结处理。实验在万能材料试验机上完成,试件中心放在底板上,上板以3 mm/min的速度向下移动，通过计算机自动记录载荷-位移曲线。空管与填充管的变形通过照相机以间隔40~60 s记录。

图1　铝合金的拉伸应力-应变关系曲线Fig.1　Tensile stress-strain curve of aluminum alloy

图2　泡沫铝的应力-应变关系曲线Fig.2　Stress-strain curve of aluminum foam

图3　圆管的实验与模拟变形模态对比Fig.3　Comparison of experimental and simulativedeformation modes of tube

图4　圆管的实验与模拟载荷-位移曲线对比Fig.4　Comparison of experimental and simulativeforce-displacement curves of tube

图3和图4分别给出了直径为20 mm,高度为30 mm,壁厚为1.7 mm的铝合金圆管在准静态压缩实验与有限元模拟中的变形模态与载荷-位移曲线图。由图可知,圆管的准静态实验和数值模拟中变形模态相似,都产生了2个轴对称的褶皱,并且都是向外折叠,圆管的下端都是向外翻出,没有形成第三个完整的褶皱。数值模拟的载荷-位移曲线与准静态实验吻合较好。

图5和图6分别给出了直径为30 mm,高度为30 mm,壁厚为1.2 mm,泡沫铝密度为0.33 mg/mm3的泡沫铝填充管在准静态压缩实验和数值模拟中的变形模态与载荷-位移曲线。从图中可以看出,数值模拟与准静态实验中的变形模态基本相同,均产生了2个轴对称的褶皱,载荷-位移曲线吻合较好。

图5　泡沫铝填充管的实验与模拟变形模态对比Fig.5　Comparison of experimental and simulativedeformation modes of foam-filled tube

图6　泡沫铝填充管实验与模拟载荷-位移曲线对比Fig.6　Comparison of experimental and simulativeforce-displacement curves of foam-filled tube

2数值模拟结果与讨论

2.1圆管的承载力和吸能

分别对不同高度h、不同壁厚d、不同直径D的铝合金圆管进行准静态轴向压缩载荷下的数值模拟,分析了几何尺寸对其承载力和吸能性能的影响。圆管的材料为铝合金,与实验中的材料参数相同。

图7给出了直径30 mm,高度45 mm,壁厚d分别为0.9,1.2,1.5 mm的3种不同圆管的载荷-位移曲线、吸能-位移曲线,以及平均载荷-位移曲线。从载荷-位移曲线a可以看出,圆管的轴向压缩过程分为明显的3个阶段:初始弹性阶段,稳定渐进屈曲阶段，密实化阶段。随着壁厚的增大,圆管的承载力也增大,其初始峰值载荷、平均载荷以及总能量吸收都有提高。

图7　不同壁厚d的圆管准静态轴向压缩曲线Fig.7　Curves of tubes with different thicknesses d under quasi-static axial compression

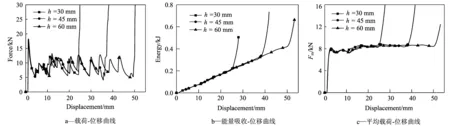
图8　不同高度h的圆管准静态轴向压缩曲线Fig.8　Curves of tubes with different heights h under quasi-static axial compression

图8为直径30 mm,壁厚0.9 mm,高度h分别为30,45,60 mm的3种不同圆管的载荷-位移曲线、吸能-位移曲线以及平均载荷-位移曲线。由图可知,圆管的轴向压缩位移随着高度的增加而增大。在进入密实阶段之前,不同高度的圆管的初始峰值载荷、平均载荷以及总能量吸收基本相同。因此在选择圆管的高度时主要考虑所需要的压缩行程。

图9为壁厚1.5 mm,高度45 mm,直径D分别为30,35,40 mm的3种不同圆管的载荷-位移曲线、吸能-位移曲线以及平均载荷-位移曲线。从图中可以看出，圆管的直径越大,压缩到同一位移时的压溃力、平均载荷以及能量吸收都越大，管的初始峰值载荷也随着直径的增大而增大。

图9　不同直径D的圆管准静态轴向压缩曲线Fig.9　Curves of tubes with different diameters D under quasi-static axial compression

2.2泡沫铝填充圆管的承载力和吸能

泡沫铝填充管中的外部金属圆管与上一节中的圆管几何尺寸相同,泡沫铝的直径为管的内径,高度与外管的高度相同,其外部的圆管与泡沫铝的材料参数与实验中试件的材料参数相同。

图10　不同壁厚d的泡沫填充管准静态轴向压缩曲线Fig.10　Curves of foam-filled tubes with different thicknesses d under quasi-static axial compression

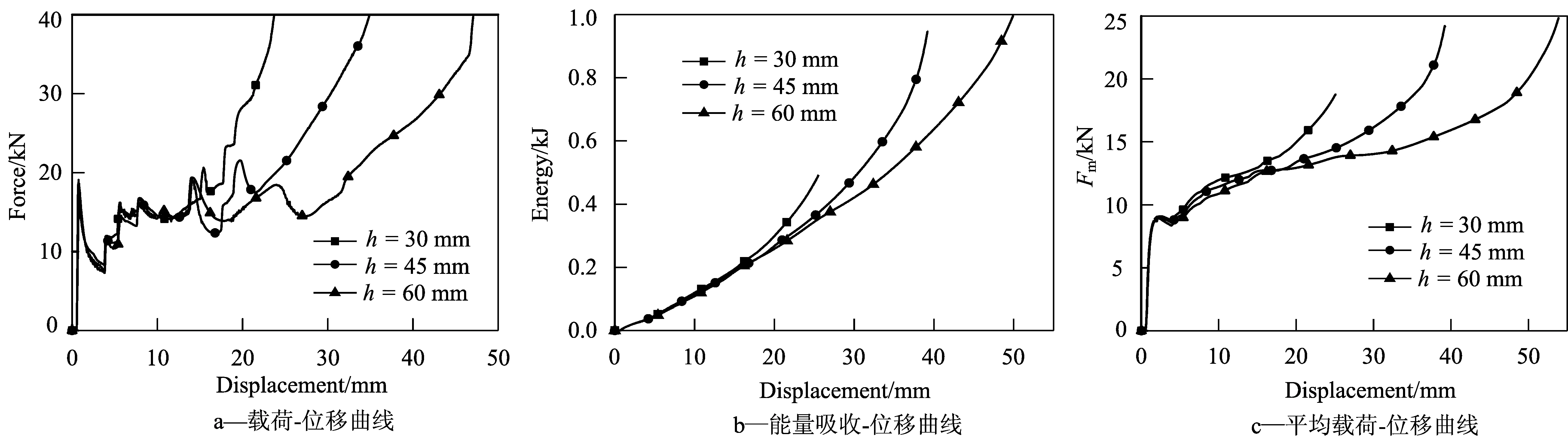
图11　不同高度h的泡沫填充管准静态轴向压缩曲线Fig.11　Curves of foam-filled tubes with different heights h under quasi-static axial compression

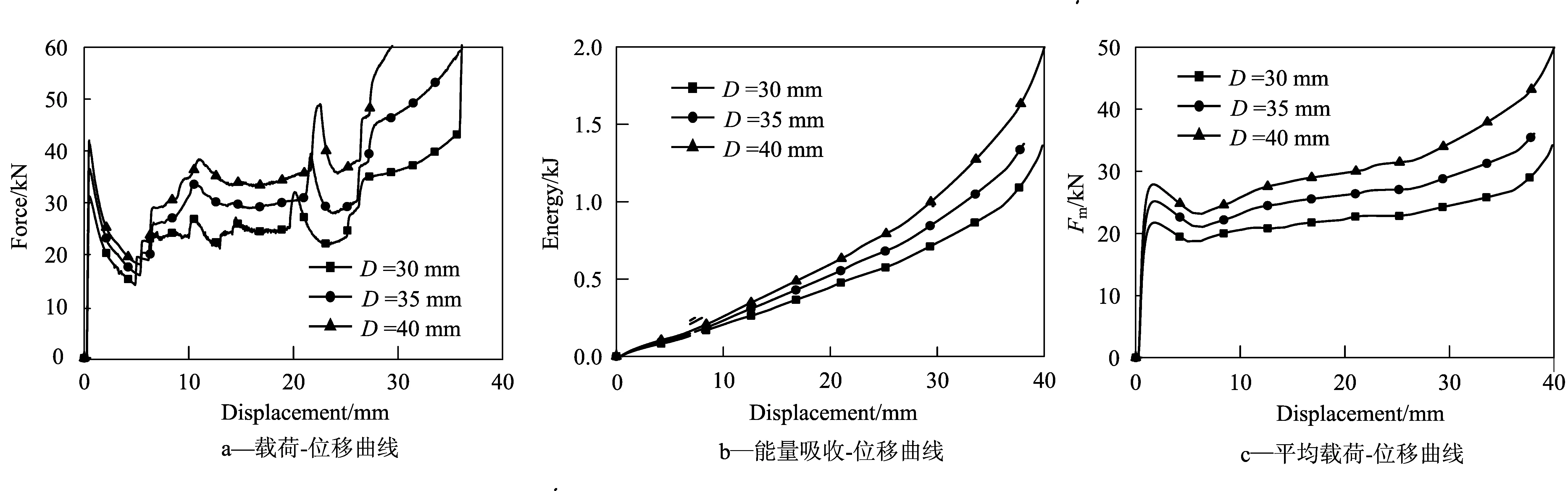
图12　不同直径D的泡沫填充管准静态轴向压缩曲线Fig.12　Curves of foam-filled tubes with different diameters D under quasi-static axial compression

图10—图12分别给出了不同的壁厚d、不同高度h、不同直径D的泡沫铝填充圆管的载荷-位移曲线、吸能-位移曲线以及平均载荷-位移曲线。可以看出,与圆管相比,泡沫铝填充管的轴向载荷波动较小,在达到初始峰值载荷之后,呈逐渐上升趋势。其原因可能是在轴向压缩过程中,圆管和填充物泡沫铝之间存在相互作用,这种相互作用效应随着压缩位移的增大而增大,并且泡沫铝本身也随着压缩位移的增大而逐渐被压实。泡沫铝填充管的平均载荷随着位移的增大而逐渐增大,不同于空管的平均载荷在渐进屈曲阶段几乎保持不变的情况。由图10可知,随着填充管壁厚的增加,其初始峰值载荷、平均载荷和总吸能增加。由图11可以看出,填充管的高度对其初始峰值载荷、平均载荷和总吸能的影响较小,在密实化之前,不同高度填充管的压缩载荷、总吸能与平均载荷几乎重合,表明填充管的吸能与管的高度成线性关系。由图12可知,随着填充管直径的增加,其初始峰值载荷、总吸能,平均载荷都增大。

2.3吸能指标

为评价泡沫铝填充管与圆管的耐撞性,引入了以下几种参数[10]:

1) 初始峰值载荷Fmax;

2) 压缩到某一位移时的总吸收能量E;

3) 比吸能ESA(Specific Energy Absorption),即单位质量的试件所吸收的能量:

(1)

式中:m为对应模型的质量;F为管在某时刻的轴向压缩载荷;l为该时刻载荷所对应的位移值。

4) 压缩到某一位移时的平均载荷Fm:

(2)

5) 压缩力效率ECF(Crush Force Efficiency),

定义为初始峰值载荷Fmax与平均载荷Fm之比:

(3)

表1给出了不同尺寸的泡沫铝填充管和圆管在压缩距离为初始管长的80%时的各项吸能指标。

表1　圆管及泡沫填充管的吸能评价指标

2.3.1不同壁厚的泡沫填充管与圆管的吸能性能

考虑直径为30 mm,高度为45 mm,壁厚d分别为0.9,1.2,1.5 mm的泡沫填充管与空圆管的吸能指标。表1给出了压缩距离为原管长的80%时的比吸能、平均载荷、初始峰值载荷及压缩力效率，可以看出，空管的比吸能、平均载荷、初始峰值载荷及压缩力效率都随着管壁厚的增大而增大。每一种规格的空管填充了泡沫铝之后,其各项吸能指标都较原来有所提高；但不同壁厚的管填充泡沫之后吸能指标提高的程度有所差别，壁厚越小的管件,对应的泡沫铝填充管的各项吸能指标提升的比例越大,即泡沫填充效果越明显。如，壁厚为0.9 mm的圆管填充泡沫铝之后其比吸能、平均载荷、初始峰值载荷及压缩力效率较原来分别提高了17.7%,125.8%,4.4%,116.5%；壁厚为1.2 mm的填充管相应指标分别提高了5.3%,76.3%,3.2%,70.8%；壁厚为1.5 mm的填充管对应的数值为1.9%,55.7%,2.2%,53%。

2.3.2不同高度的泡沫填充管与圆管的吸能性能

为对比直径为30 mm,壁厚为0.9 mm,管的高度h分别为30,45,60 mm的泡沫填充管与空圆管的吸能性能,表1给出了其压缩距离为初始管长的80%时的比吸能、平均载荷、初始峰值载荷及压缩力效率值。从表中可以看出，泡沫铝填充管的比吸能、平均载荷、初始峰值载荷与压缩力效率均高于空管。随着高度的增加,这些指标的变化较小,表明高度对泡沫铝填充管与空管的吸能性影响较小。因而增加泡沫铝填充管或空管的高度,可以增加其可利用的压缩距离，从而使整体结构的总能量吸收得到提高,对其他吸能指标的影响较小。该组对比中泡沫铝填充管的压缩力效率都大于1,这是由于该组模型壁厚都较薄；管的壁厚越薄,填充结构受轴向压缩时泡沫铝的承载力与吸能所占比例越大；随着压缩位移的增大,管和泡沫之间的相互作用也随之增大,泡沫铝也慢慢被压实,使得压缩载荷在达到峰值之后呈现逐渐上升趋势,因而压缩力效率较高。

2.3.3不同直径的泡沫填充管与圆管的吸能性能

考虑高度为45 mm,壁厚为1.5 mm,直径D分别为30,35,40 mm的泡沫铝填充管与空圆管的吸能指标。从表1给出的泡沫填充管与空圆管的比吸能、平均载荷、初始峰值载荷及压缩力效率对比中可以看出，泡沫铝填充管的各项吸能指标均高于空管。随着直径的增大,泡沫铝填充管的比吸能、平均载荷与压缩力效率较空管增加的比例增大。如，直径为30 mm的管件填充泡沫铝之后其比吸能、平均载荷及压缩力效率较空管分别提高了1.9%，55.7%，53%；直径为35 mm的填充管相应指标分别提高了10.4%，78.3%，70.8%；直径为40 mm的填充管对应的数值为20.8%，109.2%，105.9%。空管的初始峰值载荷以及平均载荷都随着管直径的增大而增大,相反的比吸能以及压缩力效率都随着管的直径的增大而减小。

3结论

利用有限元软件ABAQUS对泡沫铝填充薄壁金属圆管和圆管在轴向准静态压缩时的吸能性能进行了数值模拟。首先，通过与实验结果的对比验证了有限元模型的有效性与计算的可靠性；之后，根据建立的模型系统地研究了管的高度、壁厚、直径以及泡沫铝的填充对圆管吸能性能的影响；利用初始峰值载荷、平均载荷、总吸能与比吸能等吸能评价指标对结构的吸能特性进行了分析。结果表明,铝合金圆管受到轴向压缩时的载荷-位移曲线分为明显的三个阶段:初始弹性阶段，塑性变形阶段，密实化阶段。圆管在准静态轴向压缩时的初始峰值载荷、平均载荷、总吸能、比吸能随着管壁厚的增加而增大;初始峰值载荷、平均载荷以及总吸能随着管直径的增大而增大，但是比吸能和压缩力效率随管直径的增大而减小;当管的高度增大时,其比吸能、平均载荷、初始峰值载荷及压缩力效率都没有发生明显变化,即高度对空管的吸能效率影响不是很大，与空管相比,泡沫铝填充管的比吸能、平均载荷、初始峰值载荷及压缩力效率均高于对应的空管,但增大的程度随着管的几何参数的不同而变化。填充管的壁厚越小,其各项吸能指标较空管提升的比例越大;填充管的直径越大,其比吸能、平均载荷、压缩力效率增大的比例越大;填充管的高度对泡沫填充管的吸能性能影响较小。研究表明，泡沫铝填充薄壁金属圆管是一种理想能量吸收元件。

参考文献：

[1]ANDREWS K R F,ENGLAND G L,GHANI E.Classification of the axial collapse of cylindrical tubes under quasi-static loading[J].International Journal of Mechanical Sciences,1983，25(9/10):687-696.

[2]GUILLOW S R,LU G,GRZEBIETA R H.Quasi-static axial compression of thin-walled circular aluminium tubes[J].International Journal of Mechanical Sciences,2001,43(9):2103-2123.

[3]CHEN D H,VSHIJIMA K.Estimation of the initial peak load for circular tubes subjected to axial impact[J].Thin Walled Structures,2011,49(7):889-898.

[4]KARAGIOZOVA D,NORMAN J.Dynamic effects on buckling and energy absorption of cylindrical shells under axial impact[J].Thin-Walled Structures,2001,39(7):583-610.

[5]SEITZBERGER M,RAMMERSTORFER F G,DEGISCGER H P,et al.Crushing of axially compressed steel tubes filled with aluminium foam[J].Acta Mechanica,1997,125(1/2/3/4):93-105.

[6]桂良进,范子杰,王青春.泡沫填充圆管的轴向压缩能量吸收特性[J].清华大学学报(自然科学版),2003,43(11):1526-1529.

[7]桂良进,范子杰,王青春.泡沫填充圆管的动态轴向压缩吸能特性[J].清华大学学报(自然科学版),2004,44(5):709-712.

[8]SANTOSA S,WIERZBICKI T.Experimental and numerical studies of foam-filled sections[J].International Journal of Impact Engineering,2000,24(5):509-534.

[9]张志新,田爱琴,车全伟,等.高速列车车体端部吸能结构研究[J].机车电传动,2013(1):43-47.

[10]李志斌,虞吉林,郑志军,等.薄壁管及其泡沫金属填充结构耐撞性的实验研究[J].实验力学,2012,27(1):77-86.

(编辑：庞富祥)

Study on Energy Absorption Properties of Thin-walled Circular Tubes Filled with Aluminum Foam under Axial Compression

HUANG Rui,LIU Zhifang,LU Guoyun,YAN Qingrong

(InstituteofAppliedMechanicsandBiomedicalEngineering,TaiyuanUniversityofTechnology,Taiyuan030024,China)

Abstract:Numerical simulation analysis of tubes filled with aluminum foam of seven different geometric sizes under quasi-static axial compression was conducted using the finite element software ABAQUS. The influence of the height,thickness and diameter of tubes on the energy absorption properties of the tubes and the foam-filled tubes was studied systematically.Comparative analysis was conducted on the evaluation indexes of energy absorption such as average load,initial peak load, specific energy absorption (ESA) and compression force efficiency (ECF) for seven types of foam-filled tubes. The results show that the thickness and diameter of the tubes have a significant effect on energy absorption properties of the structures when the tubes with aluminum foam filler are under quasi-static axial compression.The effect of height is not evident but the increase of the height can improve the total energy absorption of the tube. Aluminum foam filler improves the bearing capacity,total energy absorption, specific energy absorption and compression force efficiency of the tubes. The results of the research can provide some technical basis for the design of ideal energy absorption devices.

Key words:tubes filled with aluminum foam;axial compression;energy absorption;numerical simulation

中图分类号:O347.3

文献标识码:A

DOI：10.16355/j.cnki.issn1007-9432tyut.2016.01.020

作者简介：黄睿(1991-),女,山西运城人,硕士生,主要从事泡沫铝夹芯冲击动力学研究,(E-mail)rui152@126.com通讯作者：闫庆荣(1960-),女,高级工程师,主要从事冲击动力学研究,(E-mail)yanqingrong@tyut.edu.cn,(Tel)0351-6010560

基金项目：国家自然科学基金资助项目:浆砌多级构建(层合)壳体的冲击动力学行为研究(11372209);山西省自然科学基金资助项目:柱壳结构中的非线性弥散波与波致失效的研究(2013011005-2)

收稿日期：2015-04-30

文章编号:1007-9432(2016)01-0101-07