空心金属光纤导引原子和Monte-Carlo模拟

赵连洁，严小军，张国万, 张安宁

（北京航天控制仪器研究所，北京 100039）

空心金属光纤导引原子和Monte-Carlo模拟

赵连洁，严小军，张国万, 张安宁

（北京航天控制仪器研究所，北京 100039）

在空心金属光纤，首先计算了TE01模的电磁场分布和光强分布。其次以85Rb原子为例，计算了TE01模和85Rb原子相互作用的光学势。研究表明，TE01模在空心金属光纤中集中分布在空心区，沿光纤截面呈环状分布。最后采用Monte-Carlo方法，分别模拟了原子在直空心金属光纤和弯曲空心金属光纤中的直导引效率和弯曲导引效率，相比直导引方案，弯曲导引方案效率明显偏低。空心金属光纤原子导引不仅可用于原子干涉仪研究，采用环形空心金属光纤的原子导引还可用于角速度测量研究。

原子导引；Monte-Carlo模拟；空心金属光纤；导引效率；光学势

空心光纤原子导引技术能够控制原子沿特定路径移动，实现原子的精确导引和控制，这在原子光学实验中具有重要应用价值[1]，可用于原子漏斗[2]、原子刻印

[5]、原子干涉[6]和原子分束器[8]等的研制，尤其在原子干涉陀螺仪研制中能有效解决原子团分束角度小的问题[7]。1993年，俄罗斯M. A. Ol’Shanii等人首先提出采用红失谐高斯模式的激光场来导引中性原子思想[9]。1994年，澳大利亚S. Marksteiner等人基于蓝失谐消逝波光场也提出了蓝失谐消逝波光场的原子导引方案[10]。1995年，美国JILA的Cornell小组在实验上首先实现了上述两种导引方法的实验验证[11]，但导引效率较低。之后还陆续出现了很多光纤导引原子的实验研究，但都存在导引效率较低的问题。为提高原子的导引效率，1999年，Herschel S. Pilloff等人提出采用空心金属光纤导引原子的思想[12]，空心金属光纤的空心区域尺寸较大，约为几十个微米，可以大大提高原子的导引效率。2005年，印建平小组提出了一种采用空心金属光纤中TE01模式实现原子导引的新方案，并对空心金属光纤中TE01模实现原子导引的理论进行了分析[13]。但是由于原子光学实验发展限制，到目前为止还未见有空心金属光纤中导引原子的实验研究报道。

本文基于空心金属光纤的原子导引具有较高效率的优势，就空心金属光纤中TE01模导引原子进行了研究。首先计算了空心金属光纤中TE01模的场分布、光强分布和原子与 TE01模相互作用光学势；其次采用Monte-Carlo方法分别模拟了原子在直空心金属光纤中的原子导引效率和弯曲空心金属光纤中的原子导引效率，并对直导引和弯曲导引效率和速率分布情况进行了比较；最后进行总结和展望。

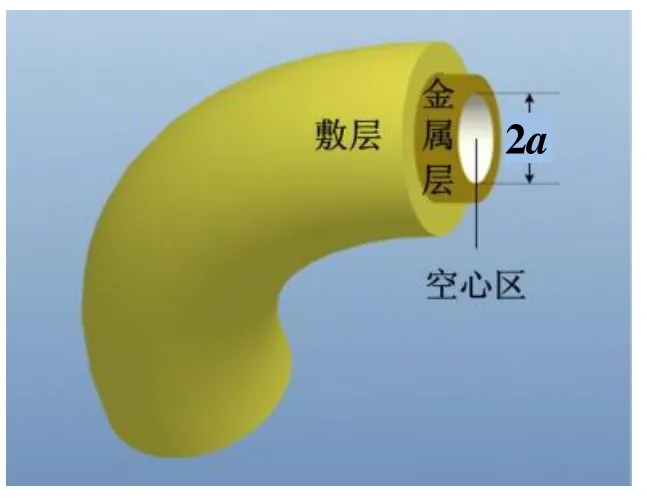
图1 空心金属光纤示意图Fig.1 Hollow metallic optical fiber

1 空心金属光纤中TE01模原子导引

1.1 空心金属光纤中TE01模的场分布

本文研究的空心金属光纤由空心区、金属层和敷层构成，如图1所示。空心区内径一般为几十个微米，具有较高的真空度；金属层为一层薄的金属薄层，构成了限制激光传输和原子导引的空心区域；敷层用于保护金属薄层与外界隔离。

将激光耦合进入空心金属光纤将会激发出三种传输模式：横电模 TE0m模、横磁模 TM0m模和混杂模EHnm模。根据空心金属光纤中电磁场的传输损耗研究发现，空心金属光纤不仅对TE0m模具有模式选通作用，对TM0m模和EHnm模还具有模式滤波作用，因此在空心金属光纤中TE0m模具有较高的传输效率。本文主要研究TE0m模的最低阶模式TE01模。

根据空心金属光纤中纵向和横向分量间的一般关系式，可以得到TE01模在空心金属光纤中的电磁场分布：

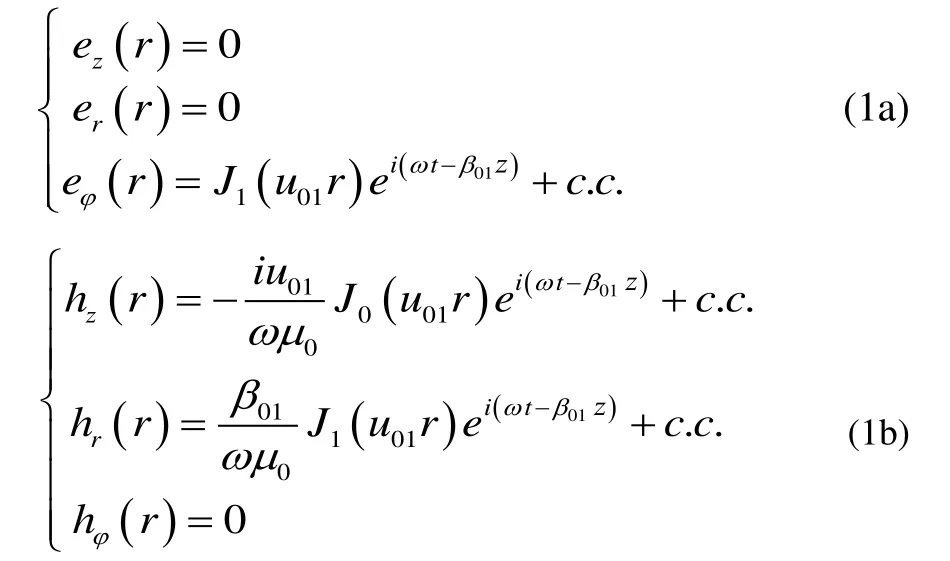
电磁场中的电场分量通常是磁场分量的几百倍甚至几千倍，在讨论光场强度时通常只考虑电场分量，而忽略磁场分量。在仅考虑电场分量条件下，空心金属光纤中TE01模的径向强度分布可以表示为

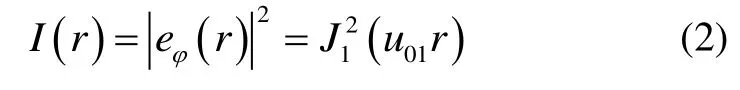
分析一般情况，选取空心区半径a分别为15 μm、20 μm、30 μm的空心金属光纤，可以得到三种空心金属光纤中TE01模的场分布和强度分布，如图2所示。

从图2可以看出：在空心金属光纤中TE01模集中在空心区，在光纤轴线位置强度为零，且强度分布沿光纤轴线呈圆环形；对于不同内径空心金属光纤，各光强梯度存在很大差别。

图2 空心金属光纤中TE01模场分布和强度分布Fig.2 Distributions of TE01mode in hollow metallic optical fiber

1.2 冷原子在空心金属光纤中的光学势

以上为空心金属光纤中 TE01模的场分布和强度分布。为计算TE01模与冷原子之间的相互作用光学势，还需要计算在一定输入激光功率条件下，空心金属光纤中TE01模的绝对光强分布。根据能量守恒定律，空心金属光纤中电磁场的绝对光强分布为

在此我们假设激光从自由空间被完全耦合进入空心金属光纤空心区，其中，Pin为输入光功率，I(r)为半径r处的光强分布，a为空心金属光纤空心区半径。

有了空心金属光纤中电磁场的绝对光强分布，就可以得到电磁场和原子之间相互作用的光学势。对于一个二能级原子而言，电磁场和原子之间相互作用的光学势U（r）可以写成如下形式：

式中：δ为入射激光场相对于原子共振的失谐量；IS和Γ分别是原子的饱和吸收强度和自然线宽。

对于85Rb原子而言，IS=1.6 mW/cm2，Γ=6.1MHz，如果入射光场功率P=5mW，失谐量δ=10GHz ，对于半径a分别为15 μm、20 μm、30 μm的空心金属光纤，我们可以得到各空心金属光纤中 TE01模的绝对光强分布和光学势沿光纤截面的径向分布，如图3所示。

图3(a) 绝对强度沿光纤截面的径向分布Fig.3(a) Absolute intensity distribution of TE01mode against radial position for85Rb atoms with different radii

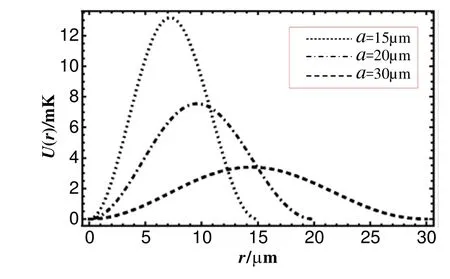
图3(b) 光学势沿光纤截面的径向分布Fig.3(b) Optical-potential distribution of the TE01mode against radial position for85Rb atoms with different radii.

从图3可以看出空心金属光纤中的绝对光强沿光纤截面呈环状分布，且随空心区半径不同光功率密度分布差别很大。光学势分布沿光纤截面同样呈环状分布，随空心区半径不同，光学势梯度分布差别很大。对于空心区半径a=20μm 的空心金属光纤，当入射光功率P=5mW，入射激光场相对于原子共振的失谐量δ=10 GHz时，在空心金属光纤内部产生的最大光学势约为7.5 mK，要远大于标准磁光阱中85Rb原子的温度（约为 120 μK），在空心区运动的原子将在该光学偶极力束缚下在空心金属光纤中心轴线附近，因此如果此时原子存在一个沿光纤轴向的速度，原子流将在偶极力作用下沿光纤轴运动。

2 原子导引效率的Monte-Carlo模拟

2.1 原子导引动力学理论

在估算原子导引效率时，我们采用经典理论模型：首先，将原子看作是一系列独立的经典粒子；其次，原子系综遵循能量守恒定律；最后，在模拟原子导引过程中，如果原子碰触到空心金属光纤内壁，就认为原子在导引过程中损失掉，而那些没有碰触空心金属光纤内壁的原子就被成功导引。同时根据TE01模在空心金属光纤中沿光纤轴线的传输损耗非常小的特点，在计算中我们认为在空心金属光纤中传输的 TE01模基本没有衰减。

假设在光纤截面入射原子的空间分布、速率分布都满足高斯分布：

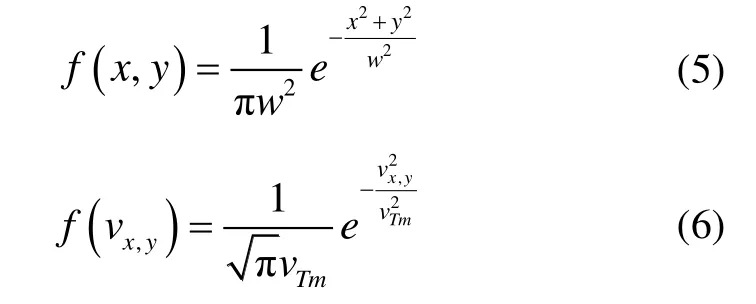
式中：w为原子系综空间分布束腰。沿z方向的速率满足修正的高斯分布：

对于直导引情况，入射到空心金属光纤空心区的原子和TE01模将会发生偶极相互作用，原子在该偶极相互作用下被束缚在空心金属光纤中心轴线附近，如果存在沿光纤轴线运动的速度，有一部分原子将在光学势束缚下在空心金属光纤中导引一定长度，而不会碰撞到光纤内壁损失掉。对于弯曲的空心金属光纤情况，对于沿空心金属光纤中心轴线方向速度较大的原子，如果其动能大于TE01模的最大光学势，该部分原子将会因为动能过大碰触到空心金属光纤内壁损失掉而不能被成功导引。尤其对于曲率半径R小于几厘米时的弯曲空心金属光纤导引原子情况，就必须考虑原子的弯曲导引效率。

2.2 直导引效率的Monte-Carlo模拟

在以上原子导引动力学理论假设基础上，我们采用 Monte-Carlo方法模拟原子在空心金属光纤空心区导引的动力学过程。参照在空芯光纤中原子和激光场相互作用产生的光学势式(4)，原子在空心金属光纤中受到的偶极力就可以表示为

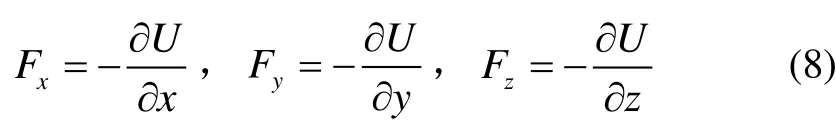
原子在空心金属光纤中的运动加速度为

我们基于Matlab语言在包含8个CPU的并行计算机上对直空心金属光纤中原子的导引效率进行了Monte-Carlo模拟。模拟参数包括：空心金属光纤金属层为铝材Al，其复折射率η=25+i67，入射激光波长为780 nm，空心区半径a=20μm ，TE01模的直线传输损耗α01=0.138249。假设初始截面上原子的空间分布和速率分布都满足高斯分布，沿z方向的速率满足修正的高斯分布，沿光纤截面的横向温度TTm和沿光纤轴线 z方向的纵向温度TLm分别为TTm=5 mK，TLm=5K 。原子入射到空心金属光纤空心区后，将会受到光学偶极力作用沿特定路径运动，采用 Monte-Carlo方法模拟其运动轨迹。最后，我们统计出射后落在空心区域内的原子作为有效导引的原子数，其他区域原子都视为损失掉。

为了研究原子在直空心金属光纤中直导引效率和入射激光功率的关系，我们对包含10 000个原子的原子束流进行了6次Monte-Carlo模拟，得到如图4所示的出射原子数和入射激光功率之间的关系曲线。

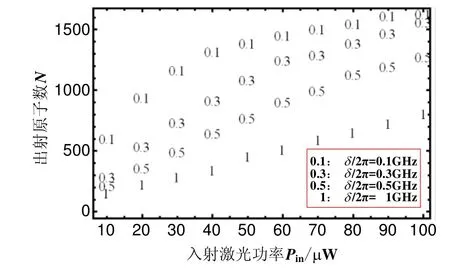
图4 出射原子数和入射激光功率的关系曲线Fig.4 Relationship of between the number of exiting atoms and the incident laser power

图4中的数据点为6次Monte-Carlo模拟的平均结果，从图4可以看出，在一定入射激光功率范围内被成功导引的原子数将随激光功率的增大逐渐上升。当入射激光功率为0.1 mW，入射激光场相对于原子共振的失谐量时，原子的导引效率为7.94%；当入射激光场相对于原子共振的失谐量δ2π=0.1GHz时，原子的导引效率达16.22%。

为了进一步研究直空心金属光纤中原子导引后的速度分布，当入射激光场相对于原子共振的失谐量我们对包含10 000个原子的原子束流进行了Monte-Carlo模拟，得到如图5所示出射原子束流的横向速度分布和纵向速度分布图，图中的柱状图是 Monte-Carlo模拟结果，实线分别是采用高斯分布和瑞利分布公式拟合的结果。

图5 出射原子束流的横向速度分布和纵向速度分布Fig.5 Distributions of transverse velocities (vx,vy) and longitude velocity vzfor the exiting atoms

从图5可以看出，导引前后原子的横向速度分布相差很大，而纵向速度分布相差相对较小。这主要是由于横向速度较大的原子在导引过程中很容易碰撞空心金属光纤内壁损失掉，只有横向速度较小的原子在光学偶极力的束缚下才能被成功导引。纵向速度基本不受光学偶极力作用，只有合适速度的原子被成功导引。因此在直空心金属光纤中导引原子，主要影响原子的横向速度分布，对纵向速度分布影响较小。

2.3 弯曲导引效率的Monte-Carlo模拟

为实现原子束流的弯曲传输和操作，在实际应用中空心金属光纤都呈弯曲形状，因此讨论原子的弯曲导引效率是非常必要的。在弯曲空心金属光纤中，我们引入曲线坐标系，假设空心金属光纤弯曲平面在y-z平面上，并沿z轴弯曲，那么原子在弯曲空心金属光纤中运动的加速度就可以表示为

式(10)表明原子在弯曲空心金属光纤中除了要受到光学偶极力外，还要受到一个在y-z平面上额外的惯性力作用。同样，我们采用Monte-Carlo方法模拟弯曲空心金属光纤中原子的导引效率。在弯曲导引效率模拟中我们同样采样金属层为铝材 Al的空心金属光纤，入射激光波长为 780 nm，空心区半径a=20μm，曲率半径R=2cm，TE01模的弯曲传输损耗α01=0.352466。在初始截面上同样认为原子的空间分布和速率分布满足高斯分布，沿z方向的速率满足修正的高斯分布，沿光纤截面的横向温度TTm和沿光纤轴线 z方向的纵向温度TLm分别为TTm=5mK ，TLm=5K。原子束流入射到空心金属光纤空心区后，不仅受到光学偶极力所用，还要受到一个额外的惯性力作用，原子将在弯曲空心金属光纤中作曲线运动，采用 Monte-Carlo方法模拟其运动轨迹。最后，统计出射后落在空心区域内的原子作为有效导引的原子数，其他区域原子都视为损失掉。

为了研究原子在弯曲空心金属光纤中弯曲导引效率和入射激光功率的关系，同样对包含有10000个原子的原子束流进行了6次Monte-Carlo模拟，得到如图6所示的原子在弯曲空心金属光纤中弯曲导引效率和入射激光功率的关系曲线。

同样，图6中的数据点为6次Monte-Carlo模拟的平均结果。从图6可以看出：类似直导引效率，在弯曲导引中，在一定入射激光功率范围内被成功导引的原子数也随激光功率的增大逐渐上升，但是在一定入射激光功率下，不同失谐量条件下的导引效率也存在很大差别，因此在导引原子时要选择合适的激光功率和失谐量。

同样，为进一步研究弯曲空心金属光纤中原子导引后的速度分布，当入射激光场相对于原子共振的失谐量时，同样对包含有10 000个原子的原子束流进行了 Monte-Carlo模拟，如图 7所示的弯曲导引后原子束流的横向速度和纵向速度分布图，图中的柱状图是 Monte-Carlo模拟结果，实线分别是采用高斯分布和瑞利分布公式拟合的结果。

图6 出射原子数和入射激光功率的关系曲线Fig.6 Relationship between the exiting atoms and the incident laser power.

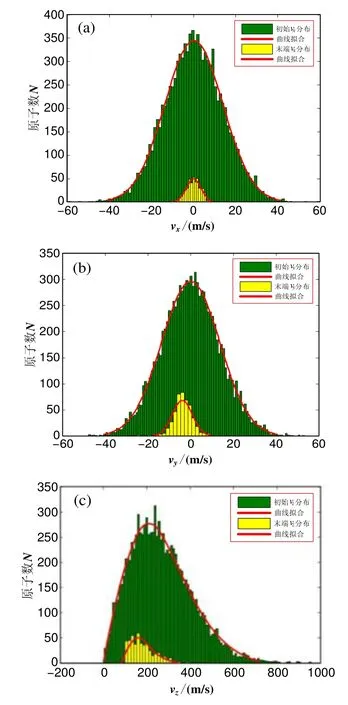
图7 出射原子束流的横y向速度分布和纵向速度分布Fig.7 Distributions of transverse velocities (vx,vy) and longitude velocity vzfor the exiting atoms

从图7可以看出，与直导引相比，弯曲导引前后原子的横向速度分布相差更为明显，原子的导引效率明显偏低。在垂直于弯曲平面x方向上横向速度vx集中分布在零点附近，而y方向上横向速度vy分布明显偏离零点，这是在y方向附件一个额外惯性力的结果。此外，与直导引相比，弯曲导引后原子的纵向速度分布更为集中，且导引后原子数明显偏低，这主要是由于纵向速度较大的原子在导引过程中很容易被抛出空心金属光纤空心区损失掉，只有合适速度的原子在光学偶极力和附加惯性力的共同作用下才能被成功导引。因此在弯曲空心金属光纤中导引原子，不仅会影响原子的横向速度分布，对纵向速度分布影响也较大，且相比直导引，弯曲导引效率偏低。

3 总结与展望

本文首先基于空心金属光纤，对TE01模的场分布和光强分布进行了计算，研究表明：空心金属光纤中的TE01模集中在空心区，在光纤轴线位置强度为零，且强度分布沿光纤轴线呈圆环形；对于不同内径空心金属光纤，各光强梯度存在很大差别，可用于实现在空心金属光纤中的原子导引。其次，针对85Rb原子，计算了当入射光功率P=5mW，入射激光场相对于原子共振的失谐量δ=10GHz 时，TE01模和原子的相互作用光学势，完成了在空心金属光纤中采用TE01模实现原子导引的可行性分析。此外，采用 Monte-Carlo方法分别模拟了原子在直空心金属光纤中的直导引效率和弯曲空心金属光纤中的弯曲导引效率，模拟结果和理论分析一致。在直导引方案中，主要影响原子的横向速度分布；在弯曲导引方案中，不仅影响原子的横向速度分布，对纵向速度分布影响也较大，且相比直导引，弯曲导引效率明显偏低。基于弯曲原子导引特点，可尝试采用环形空心金属光纤实现加速度测量研究。

（References）：

[1] 刘院省, 王巍, 王学锋. 微型核磁共振陀螺仪的关键技术及发展趋势[J]. 导航与控制, 2014, 13(4): 1-6. Liu Yuan-xing, Wang Wei, Wang Xue-feng. Key technology and development tendency of micro nuclear magnetic resonance gyroscope[J]. Navigation and Control, 2014, 13(4): 1-6.

[2] Yu J, Djemaa J, Nosbaum P, et al. Funnel with orientated Cs atoms[J]. Optics Communications, 1994, 112(3-4): 136-140.

[3] Schiffer M, Christ M, Wokurka G, et al. Temperatures near the recoil limit in an atomic funnel[J]. Optics Communications, 1997, 134(1-6): 423-430.

[4] Yoo S H, Won C, Kim J A, et al. Diffracted near field of hollow optical fibre for a novel atomic funnel[J]. J. Opt. B: Quantum Semiclass. Opt., 1999(1): 364-370.

[5] Sakaki H I K, Ohtsu M, Jhe W. Evanescent-light guiding of atoms through hollow optical fiber for optically controlled atomic deposition[J]. Appl. Phys. Lett, 1997, 70(19): 2496-2498.

[6] Lenef A, Hammond T D, Smith E T, et al. Rotation sensing with an atom interferometer[J]. Physical review letters, 1997, 78(5): 760-763.

[7] 王巍, 王学锋, 马建立, 等. 原子干涉陀螺仪关键技术及进展[J]. 导航与控制, 2011, 10(2): 55-60 Wang Wei, Wang Xue-feng, Ma Jian-li, et al. Key technology and development of atom interferometric gyroscope[J]. Navigation and Control, 2011, 10(2): 55-60.

[8] Cassettari D, Hessmo B, Folman R, et al. Beam splitter for guided atoms [J]. Phys. Rev. Lett., 2000, 85(26): 5483-5487.

[9] Ol’Shanii M A, Ovchinnikov Yu B, Letokhov V S. Laser guiding of atoms in a hollow optical fiber[J]. Optics Communications, 1993, 98: 77-79.

[10] Marksteiner S, Savage C M, Zoller P. Coherent atomic waveguides from hollow optical fibers: quantized atomic motion [J]. Physical Review A, 1994, 50(3):2680-2690.

[11] Renn M J, Montgomery D, Vdovin O, et al. Laser-guided atoms in hollow-core optical fibers[J]. Physical Review Letters, 1995, 75(18): 3253-3256.

[12] Pilloff H S. The effect of the van der Waals interaction on the excited state for atom guiding in metal-coated, hollow-core optical fibers[J]. Optics Communications, 2000, 179:123-127.

[13] Wang Zheng-ling, Dai Meng, Yin Jian-ping. Atomic(or molecular) guiding using a blue-detuned doughnut mode in a hollow metallic waveguide[J]. Optics Express, 2005, 13(21): 8406-8423.

[14] Dai Meng, Yin Jian-ping. A novel atomic guiding using a blue-detuned TE01 mode in hollow metallic waveguides [J]. Chin. Phys. Lett., 2005, 22(5): 1102-1105.

Atomic guiding of hollow metallic optical fiber and its Monte-Carlo simulation

ZHAO Lian-jie, YAN Xiao-jun, ZHANG Guo-wan, ZHANG An-ning
(Beijing Institute of Aerospace Control Device, Beijing 100039, China)

At first, the distributions of the electromagnetic field and the optical intensity are calculated for the TE01mode in hollow metallic optical fiber. Then, taking85Rb atom as an example, the optical potential between85Rb atom and TE01mode is calculated, and the study results show that the TE01mode is basically distributed in the hollow region of the metallic optical fiber, i.e. it is circularly distributed along the fiber cross section. Finally, the guiding efficiencies of the straight guide and the bent guide in the hollow metallic optical fiber are simulated respectively by Monte-Carlo method, which show that the guiding efficiency by the bent scheme is obviously lower than that by the straight scheme. The characteristics of the bent guiding scheme show that the atomic guiding in hollow metallic optical fiber not only can be used in atom interference, but also can be used as a velocity measurement instrument based on a circular hollow metallic optical fiber.

atomic guiding; Monte-Carlo simulation; hollow metallic optical fiber; guiding efficiency; optical potential

O431.1

：A

2016-08-14；

：2016-10-26

国家自然科学基金（11304007）；国家自然科学基金（61501015）

赵连洁（1985—），女，博士研究生，主要从事原子波导方面的研究。E-mail: ap_mail@yeah.net

联 系 人：严小军（1972—），男，研究员，博士生导师。E-mail: yanxiaojun@139.com

1005-6734(2016)06-0809-06

10.13695/j.cnki.12-1222/o3.2016.06.020