提高载体驱动硅微陀螺灵敏度的方法
2016-04-15张增平张福学乔晓华
张增平,张福学,乔晓华,张 岚
(1. 内蒙古财经大学 计算机信息管理学院,呼和浩特 010070;2. 北京信息科技大学 传感技术研究中心,北京 100101)
提高载体驱动硅微陀螺灵敏度的方法
张增平1,2,张福学2,乔晓华1,张 岚1
(1. 内蒙古财经大学 计算机信息管理学院,呼和浩特 010070;2. 北京信息科技大学 传感技术研究中心,北京 100101)
载体驱动硅微陀螺是一种利用体微工艺制备的新型电容式振动MEMS陀螺,它安装于旋转飞行器上,利用载体的自旋作为驱动。当载体发生横向转动时,敏感质量受到周期性科氏力的作用,产生振动,从而敏感输入角速度。针对该种MEMS陀螺,首先介绍了陀螺的工作原理和电容式检测结构,然后详细分析了差分电容与敏感质量偏转角之间的关系,最后提出了一种通过调节电容拾取电路的脉冲信号的占空比,来提高陀螺灵敏度的方法。实验测试结果表明,当占空比由50%调整到75%时,相应输出电压峰峰值可由10.7 V提高到13.1 V,提高幅度达22.43%。理论分析和实验结果均表明,该方法可简便有效地提高陀螺灵敏度,具有实际应用价值。
陀螺灵敏度;占空比;电容式检测结构;MEMS陀螺
微机械MEMS陀螺是一种利用IC工艺加工制作的新型陀螺。它具有尺寸小,重量轻,响应快,抗冲击能力强,适用于恶劣环境等优点[1-2]。MEMS陀螺以其优越的特点,有着十分喜人的应用前景,例如,计算机鼠标、智能手机稳定系统、飞行器姿态控制系统等[3-6]。
微机械陀螺的种类很多,不过绝大多数是利用科里奥利力的振动式微机械陀螺[7-10]。它们的工作原理是:由弹性挂件将敏感质量块悬挂在基座上,敏感质量块在驱动力的作用下产生振动,当基座发生转动时,产生作用于敏感质量块上的科里奥利力,科氏力使质量块沿着与驱动力相垂直的方向发生位移,位移大小与基座转动角速度成比例,实现输入角速度的敏感。通常为了获得较大灵敏度,设计中往往通过匹配驱动结构以及检测结构的谐振频率,使得位移达到最大。其缺点是系统中引起频移的各种变量很容易被陀螺敏感,从而引入误差,而且在高品质因子条件下,灵敏度较高,往往工作带宽变得较窄[11]。本文所研究的对象也是一种基于科氏效应的振动式微机械陀螺[12],但结构设计不同于常规微机械陀螺,其本身没有驱动结构,只有检测结构。它安装于旋转飞行器载体上,巧妙利用载体的自旋获得角动量。当载体发生横向转动时,随着载体的自旋,产生周期性变化的科氏力,使敏感质量产生振动,振动幅度与输入角速度成比例,从而敏感载体的输入横向角速度。我们将该陀螺称之为载体驱动硅微陀螺,其结构是敏感质量块通过两端的弹性支撑梁悬挂于外框上,外框与基座固连。当敏感质量块受到周期性科氏力的作用,会产生转动,转动受到两端支撑梁的约束。文献[13]显示,敏感质量的转动角位移与支撑梁的抗扭转刚度系数成反比,而刚度系数又取决于支撑梁的尺寸。在结构上,为了获得较大的转动角位移,提高灵敏度往往需要调节支撑梁的尺寸,但是通过体微机械加工实现梁尺寸的精确控制在工艺上比较困难。所以,利用微机械尺寸的调整进而提高陀螺的灵敏度是不现实的。为此,本文基于载体驱动硅微陀螺的敏感机理和电容检测结构,提出一种新的提高陀螺灵敏度的方法,该方法是利用调节电容拾取电路的脉冲信号的占空比,可方便有效实现陀螺灵敏度的提高。
1 陀螺工作机理
1.1 结构原理
陀螺的敏感元件是在单晶硅晶圆上,利用体微机械加工工艺制备而成。其结构原理如图1所示,由一个敏感质量块,通过两端对称的弧形扭转梁悬挂在硅基的外框架上构成。敏感质量块上刻蚀有用于调节阻尼的阻尼条和方孔,外框架与基座固连。
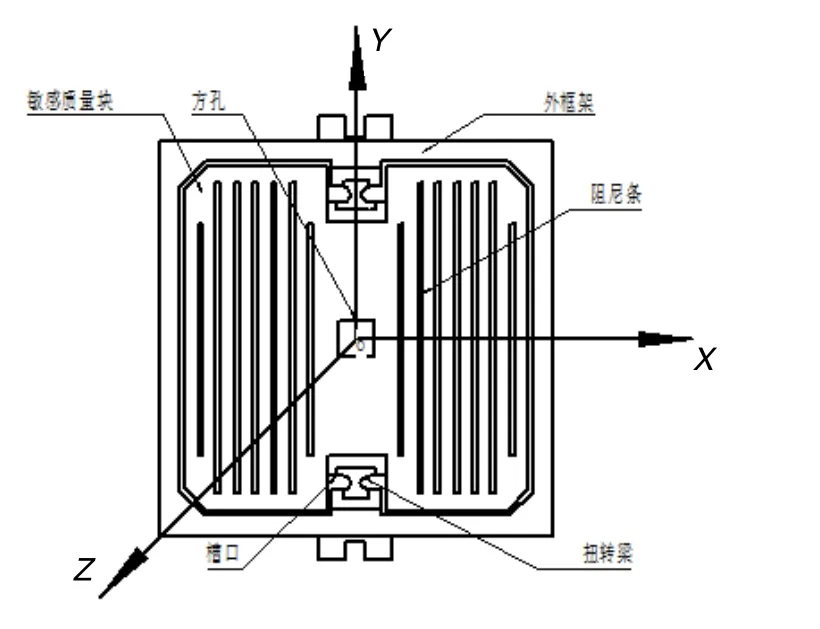
图1 敏感元件结构原理图Fig.1 Structure schematic of sensing element
参看图1,直角坐标系oxyz固定于敏感质量块上,原点o位于质心。设y轴为陀螺的输出轴(进动轴),x轴为输入轴,z轴为驱动轴。沿着y轴方向,扭转梁形成一个约束中心,敏感质量可以绕着y轴产生进动运动,其进动的振动模态如图2所示。

图2 敏感质量的振动模态Fig.2 Vibratory modal of sensing mass
载体驱动硅微陀螺是一种新型的MEMS陀螺。不同于常规科氏振动MEMS陀螺,它没有驱动结构,只有检测结构。它安装于旋转飞行器上,利用旋转载体的自旋获得角动量。
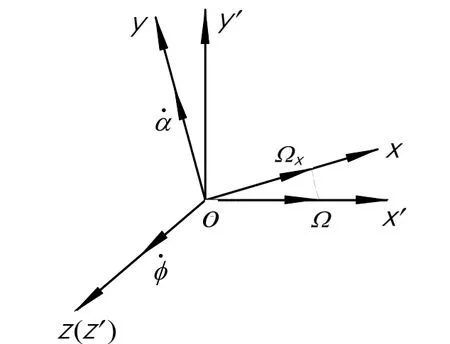
图3 敏感质量块的进动运动Fig.3 Precession motion of sensing mass
图3是敏感质量块进动运动的示意图,图中有两个直角坐标系。其中坐标系oxyz与敏感质量块固连,称为动坐标系,它的驱动轴z轴与飞行器的纵轴相重合,动坐标系将随着飞行载体一起以角速度φ˙绕z轴旋转。坐标系ox′y′z′不随载体的自旋而旋转,称之为准载体坐标系。
图 3显示,当载体发生角速度为Ω的横向转动时,它在输入轴x上的投影为xΩ,则敏感质量将受到科氏力的作用,产生沿输出轴y的进动运动,角速度为α˙。进动力矩将由三个力矩进行平衡,共同构成一个力的闭合回路系统,其中,三个平衡力矩分别是扭转梁产生的弹性力矩、质量块运动产生的阻尼力矩以及惯性力矩。
当输入轴x与准载体坐标系的x′轴重合时,敏感质量的偏转角α为零;当x与x′成90°时,偏转角α达到最大;当x与x′反向时,偏转角α为零;当x与x′成270°时,偏转角α为反向最大。随着载体继续旋转,当x与x′再次重合时,偏转角α再一次回到零位,如此循环往复,敏感质量块将产生周期性振动,振动频率对应于载体的自旋频率,振动幅度与横向输入角速度Ω的大小成比例。
1.2 角振动方程
随着载体的自旋,敏感质量块将在科氏力的作用下,绕着输出轴将产生周期性振动,如图4所示。

图4 周期性振动示意图Fig.4 Schematic diagram of periodic vibration
由结构原理可知,敏感质量块的进动运动属于刚体绕定点转动的问题,因此,可运用欧拉动力学方程进行描述。
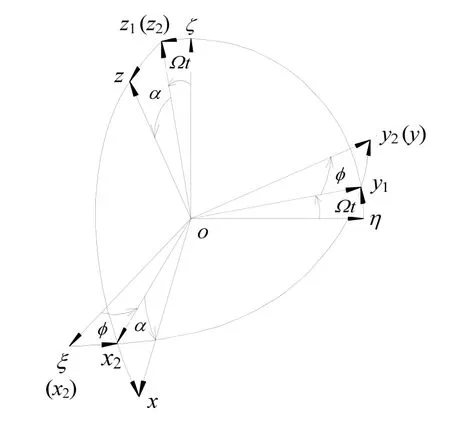
图5 坐标系变换Fig.5 Transformation of the coordinate systems
为了推导敏感质量块的角振动方程,如图5所示,我们在敏感质量块上建立4个参考坐标系,进行运动的描述。
令坐标系oξης是惯性系,o x1y1z1是载体偏航或俯仰坐标系,ox2y2z2是载体自旋坐标系,oxyz是与敏感质量块固连的动坐标系。
运动描述的顺规为:首先,在惯性系oξης中绕oξ轴以输入角速度Ω旋转至ox1y1z1,夹角为Ωt;然后,在ox1y1z1中绕oz1轴以自旋角速度φ˙旋转至ox2y2z2,夹角为φ;最后,在ox2y2z2中绕oy2轴以振动角速度旋转至oxyz,夹角为α。夹角都是关于时间的函数。
则根据动量矩定理及坐标变换,可推导出敏感质量块的角振动方程为[12]

2 灵敏度分析
2.1 灵敏度与扭转梁的关系
考虑到实际情况,飞行器的自旋频率远大于横向输入角速度,即>>Ω,而且偏转角α非常小,则有以下的近似:sinα≈α,cos2α≈cosα≈1,忽略Ω2和dΩdt。
如此,对角振动方程式(1)进行化简并求解,可得敏感质量块绕输出轴振动的稳态解为[12]

式中:Jx、Jy、Jz分别是敏感质量绕惯性主轴的转动惯量,β是偏转角和输入横向角速度的相位差。
由式(2)可知,敏感质量块的振动幅度αm与输入角速度Ω成正比,即

则,机械灵敏度为

敏感质量块在平面oxy上是对称的,所以有Jz≈Jx+Jy。另外,考虑到加工工艺的复杂性,在结构设计和封装中,往往使得KT>>Dφ˙。因此,式(4)可化简为

式(5)显示,机械灵敏度与扭转梁的抗扭转刚度系数KT成反比。因此,减小刚度系数可以增加陀螺的灵敏度。这里KT为[13]

式中:w、t、l分别是扭转梁的宽度、厚度和长度,G是弹性模量。
式(6)表明,刚度系数KT随梁的厚度t变化最显著,所以通常将梁的厚度刻蚀薄,减小抗扭转刚度,从而提高灵敏度。但是,在实际加工过程中,梁的厚度仅有几十个微米,湿法刻蚀很难保证精度和平整度,因此,会引入误差和机械噪声。
2.2 灵敏度与间隔的关系
根据该MEMS陀螺敏感元件的结构原理,敏感质量块的偏转角α较小。因此,为了尽可能减小机械噪声,同时考虑到电容随温度变化较小的特性,陀螺敏感信号的检测结构被设计为差分电容式的检测结构,如图6所示。

图6 差分电容式检测结构Fig.6 Detection structure of difference capacitors
在敏感质量块和上下厚膜极板之间,形成了 4个对称的电容C1、C2、C3和C4,对角线上的电容并联(C1和C3并联,C2和C4并联)。当敏感质量块受到科氏力作用时,以角速度α˙绕着约束中心轴(输出轴y轴)转动,此时偏转角α的变化将导致检测结构中对角线上的并联电容变化,这种变化是差动变化,从而检测敏感信号。为了计算方便,将敏感质量块进行等效,等效尺寸如图7所示。

图7 敏感质量等效结构Fig.7 Equivalent structure of sensing mass
当敏感质量块没有发生偏转,处于平衡位置(即偏转角α=0)时,C1=C2=C3=C4=C0,且有:

式中:ε为介电常数,d为质量块与厚膜陶瓷电极极板间距。
当偏转角α≠0时,C1=C3,C2=C4,电容变化为

式中:Δb是图7中实体部分的宽度,r是长度变量。对式(8)进行积分可得:

根据式(9),经过计算,差动电容为[14]
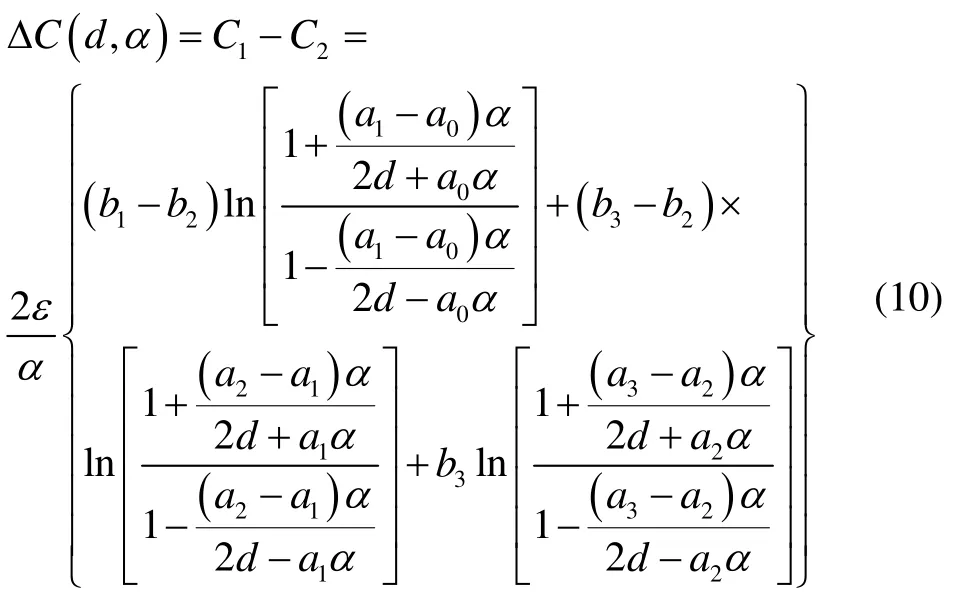
设a0=1.0 mm,a1=3.2 mm,a2=8.0 mm,a3= 10.6 mm,b1=6.8 mm,b2=3.2 mm,b3=9.6 mm,ε取8.85×10-12F/m。将这些参数代入式(10)中,可得差动电容与偏转角的关系曲线,如图8所示。间隔d分别为15 μm、20 μm、25 μm时,三条曲线分别在偏转角α为0.002 641、0.003 714、0.004 658处指数增大,这意味着在这些点处敏感质量块将接近于极板。
为了避免接触,在陀螺一定的量程下,敏感元件的结构尺寸应能控制偏转角α∈(0, 0.002),如图9所示。随着间隔的变小,差动电容对偏转角的灵敏度变大,故应尽可能减小间隔。但是,由于减小的同时,工艺加工难度也相应增加,故取固定的间隔d=15 μm。

图8 差动电容与偏转角关系曲线Fig.8 Relation between differential capacitor and deviation angle

图9 差动电容灵敏度与偏转角关系曲线Fig.9 Relational curve between sensitivity and angle
从上述分析可以看出,减小扭转梁的厚度可提高陀螺的机械灵敏度,但会引入机械噪声和误差。降低检测结构的间隔,也可以提高陀螺检测灵敏度,然而容易出现敏感质量块接触极板的情况,而且工艺上不好控制,为此只设置了一个固定的间隔。因此,综合来考虑,从结构上来进一步提高陀螺的灵敏度是不现实的。
3 提高灵敏度的新方法
3.1 差动电容拾取电路
利用电容式检测结构,由差动电容对陀螺敏感信号进行检测。接下来,需要将差动电容转换成输出电压信号。由于MEMS陀螺的敏感质量块的偏转角较小,使得电容变化率较小,所以容易受分布电容的影响。为此,转换电路采用了如图10所示的交流惠斯通电桥电路。

图10 C/V转换电路Fig.10 C/V transformation circuit
3.2 提高陀螺灵敏度的新方法
图11是交流电桥电路充放电过程示意图。当高电平时,流过电阻对电容充电;当低电平时,二极管正向导通并迅速放电。

图11 充放电过程示意图Fig.11 Schematic of charging and discharging processes
图11显示,kT≤t≤kT+T1(k=0,1,2,…)时充电,充电电压为

式中,Um是脉冲信号的高电平。
当kT+T1≤t≤(k+1)T (k=0,1,2,…)时,电容通过二极管迅速放电至Ua=Ub=0。
经过解调电路,a和b端的输出电压即为充放电全过程中的平均电压:

又根据差动电容可知:Cm= C0-ΔC和Cn= C0+ΔC,其中,C0是敏感质量块不受科氏力作用时的固有电容,ΔC是差动电容。考虑到ΔC<<C0,故Cm≈C0,Cn≈C0。令R1=R2,则由式(12)可得输出电压为[14]
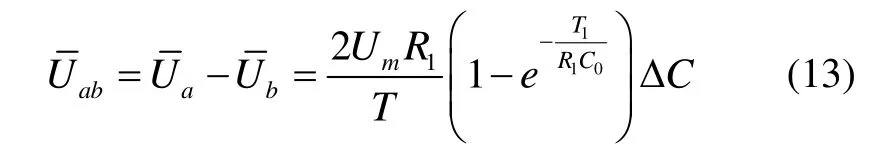
式(13)表明,输出电压和差动电容成比例,令

由式(14)可知,增加脉冲信号的占空时间T1,可提高比例系数K,从而可方便地提高陀螺的灵敏度。
4 实验验证及其结果分析
4.1 实验过程
首先,将MEMS陀螺安装于精密三轴转台的台面上,如图12所示。

图12 精密三轴转台Fig.12 Precision 3-axis turntable
精密三轴转台是模拟飞行器各种姿态运动形式的测试平台,它采用了“U-U-T”的框架结构,而且具有三个轴系,每个轴系驱动各自对应的框架。其中:内框具有一个用于安装被测陀螺的台面,内框的最大转速为18 000 (°)/s (50 Hz),它可以模拟旋转飞行器的自旋;中框和外框最大输入角速度均为 500 (°)/s,分别模拟飞行器的俯仰和偏航。
为了验证提高灵敏度的方法,需要对载体驱动MEMS陀螺的输出电压信号进行标定。

图13 标定记录Fig.13 Record in calibration
具体标定方法是:初始时,将转台复位,复位后转台的三个轴系相互垂直。接下来,将被测陀螺安装于内框的台面上,陀螺的驱动轴与内框转动轴重合,输入轴平行于外框转动轴。固定好之后,在转台控制台上将内框转速设定为5400 (°)/s (15 Hz),外框输入角速度为180 (°)/s,脉冲信号的频率为143 kHz,占空比为50%。在此工况下,通过示波器对陀螺输出信号进行记录,记录结果如图13(a)和(b)所示,脉冲信号的占空比为50%时,陀螺输出电压信号的峰峰值为10.7 V。然后,将标定好的MEMS陀螺安装在精密三轴转台的台面上。设定内框自旋频率为15 Hz,输入角速度为180 (°)/s。最后,调节脉冲信号的不同占空比,分别记录陀螺输出电压信号,其中图14(a)和14(b)是占空比为75%时的记录情况。

图14 占空比75%时的记录Fig.14 Record when duty ratio is 75%
4.2 实验结果分析
根据上述实验过程,调节脉冲信号的不同占空比,分别记录陀螺输出电压,并将输出电压信号的峰峰值记录在表1中。
将表1中的数据进行拟合,拟合后的陀螺输出电压峰峰值与脉冲信号占空比的关系曲线,如图15所示。

表1 不同占空比下的电压峰峰值Tab.1 Peak-to-peak voltages under different duty ratios
图15表明,随着脉冲信号的占空比增加,陀螺输出电压信号的峰峰值增大,也就是说,陀螺的灵敏度得到了提高。当占空比为75%时,输出电压峰峰值为13.1 V,与50%的占空比的输出电压10.7 V相比较,增大了22.43%。同时,利用陀螺信号的实验采样数据,进行信噪比计算,计算结果为29.4 dB,满足应用要求。实验结果表明,利用增加脉冲信号的占空比可有效提高陀螺的灵敏度,并具有较好的信噪比。

图15 陀螺输出电压峰峰值与脉冲信号占空比的关系曲线Fig.15 Upp(peak-to-peak voltages of gyro output) vs. duty ratio
5 结 论
本文针对一种新型的载体驱动硅微陀螺,介绍了它的敏感工作原理和角振动方程,即利用载体自旋作为驱动力,产生周期性变化的科氏力,从而敏感载体输入角速度。在此基础上,详细分析了陀螺灵敏度与敏感元件扭转梁抗扭转刚度系数的关系,以及与检测结构间隔大小之间的关系。分析结果显示,灵敏度与刚度系数成反比,刚度系数KT随梁的厚度t变化最显著,可以将梁的厚度刻蚀薄,来减小抗扭转刚度,提高灵敏度。但是,湿法刻蚀很难保证精度和平整度,会引入误差和机械噪声。另外,灵敏度随着检测结构的间隔减小而增大,为了避免质量块触碰到极板,工艺上将间隔固定为 15 μm。然后,提出一种新的提高灵敏度的方法,即可利用调节脉冲信号的占空比,有效增大陀螺灵敏度。理论分析得出:增加脉冲信号的占空时间,可提高比例系数,从而可方便地提高陀螺的灵敏度。实验验证结果表明,当占空比为75%时,输出电压峰峰值为13.1 V。与50%的占空比的输出电压10.7 V相比较,增大了22.43%,同时,陀螺的信噪比可达29.4 dB,满足应用要求。
(References):
[1] Perlmutter M, Robin L. High-performance, low cost inertial MEMS: a market in motion![C]//2012 IEEE/ION Position Location and Navigation Symposium. 2012: 225-229.
[2] 许昕, 何杰, 王文, 等. 微机械陀螺仪的新进展及发展趋势[J]. 压电与声光, 2014, 36(4): 588-595. Xu Xin, He Jie, Wang Wen, et al. Study on new development and future trends of micromachined gyroscopes[J]. Piezoelectrics and Acoustooptics, 2014, 36(4): 588-595.
[3] Gerdtman C, B Cklund Y, Lindén M. A gyro sensor based computer mouse with a USB interface: A technical aid for motor-disabled people[J]. Technology & Disability. 2012, 24(2): 117-127.
[4] Lemoyne R, Mastroianni T. Implementation of a smartphone as a wireless gyroscope application for the quantification of reflex response[C]//2014 36th Annual International Conference on Engineering in Medicine and Biology Society. 2014: 3654-3657.
[5] Kuznetsov A, Abutidze Z, Portnov B, et al. Development of mems sensors for aircraft control systems[J]. Gyroscopy & Navigation, 2011, 2(1): 59-62.
[6] Kuznetsov A G, Galkin V I, Molchanov A V, et al. MEMS IMU: Development and flight test results[J]. Gyroscopy & Navigation, 2012, 3(4): 255-264.
[7] He C, Zhao Q, Huang Q, et al. A MEMS vibratory gyroscope with real-time mode-matching and robust control for the sense mode[J]. IEEE Sensors Journal, 2015, 15(4): 2069-2077.
[8] Roland I, Masson S, Ducloux O, et al. GaAs-based tuning fork microresonators: a first step towards a GaAs-based coriolis 3-axis micro-vibrating rate gyro (GaAs 3-axis mu CVG)[J]. Sensors and Actuators A: Physical, 2011, 172 (1SI): 204-211.
[9] Guan Y, Gao S, Jin L, et al. Design and vibration sensitivity of a MEMS tuning fork gyroscope with anchored coupling mechanism[J]. Microsystem Technologies, 2015: 1-8.
[10] Prikhodko I P, Trusov A A, Shkel A M. Comparative analysis of nuclear magnetic resonance and whole angle coriolis vibratory gyroscopes[C]//2014 International Symposium on Inertial Sensors and Systems. Laguna Beach, CA, 2014: 1-2.
[11] 李锦明, 张文栋, 李林. 电容式微机械陀螺品质因子测试方法研究[J]. 中北大学学报(自然科学版). 2006, 27(4): 357-360. Li Jin-ming, Zhang Wen-dong, Li Lin. A Research on the testing method for the quality factor of capacitive microgyroscopes[J]. Journal of North University of China (Natural Science Edition), 2006, 27(4): 357-360.
[12] Zhang Z, Zhang W, Zhang F, et al. A new MEMS gyroscope used for single-channel damping[J]. Sensors (Basel, Switzerland), 2015, 15(5): 10146-10165.
[13] 张增平, 张福学, 张伟, 等. 无驱动微机械陀螺敏感元件模态分析[J]. 中国惯性技术学报, 2014, 22(5): 655-659. Zhang Zeng-ping, Zhang Fu-xue, Zhang Wei, et al. Modal analysis on sensing element of no-driven micromechanical gyro[J]. Journal of Chinese Inertial Technology, 2014, 22(5): 655-659.
[14] 张福学, 王宏伟, 张伟, 等. 利用旋转载体自身角速度驱动的硅微机械陀螺[J]. 压电与声光, 2005, 27(2): 109-117. Zhang Fu-xue, Wang Hong-wei, Zhang Wei, et al. Silicon micromachined gyro driving by angular rate of the rotating substrate[J]. Piezoelectrics & Acoustooptics, 2005, 27(2): 109-117.
Improving the sensitivity of carrier-driven Si micromechanical gyro based on duty ratio of pulse signal
ZHANG Zeng-ping1,2, ZHANG Fu-xue2, QIAO Xiao-hua1, ZHANG Lan1
(1. School of Computer & Information Management, Inner Mongolia University of Finance and Economics, Hohhot 010070, China; 2. Sensing Technique Research Center, Beijing Information Science and Technology University, Beijing 100101, China)
The carrier-driven Si micromechanical gyro is a new type of capacitive vibratory MEMS gyro, which is fabricated by using bulk micromechanical process. It is mounted on a rotating aircraft and utilizes the carrier’s spinning as the driving force. When the carrier is subjected to a transverse rotation, a periodic Coriolis force will be produced, and the input angular velocity will be sensed. In view of this type of MEMS gyro, its working mechanism and the capacitive detective structure were introduced, and the relation between the differential capacitance and the deflection angle of sensing mass was analyzed. Finally, a method for adjusting the duty ratio of the pulse signal of capacitance pickup circuit was put forward to improve the sensitivity of the MEMS gyro. Experimental tests show that the peak-to-peak voltages of gyro output is increased from 10.7 V to 13.1 V, which is increased by 22.43%, when the duty ratio is adjusted from 50% to 75%. Theoretical analysis and experimental results both show that the method can effectively improve the gyro sensitivity and has practical application value.
gyro sensitivity; duty ratio; capacitive detective structure; MEMS gyro
U666.1
:A
2016-08-11;
:2016-11-30
国家自然科学基金资助项目(61563038);内蒙古自治区高等学校创新团队发展计划支持(NMGIRT-A1609)
张增平(1969—),男,副教授、高级工程师,从事微机械惯性器件及其信号处理技术研究。E-mail: zhangzp2007@qq.com
1005-6734(2016)06-0786-07
10.13695/j.cnki.12-1222/o3.2016.06.016
