基于重力场特征参数信息熵的适配区选择方法

马越原，欧阳永忠，黄谟涛，邓凯亮，曲政豪

（1. 信息工程大学 地理空间信息学院，郑州 450052；2. 海军海洋测绘研究所，天津 300061）

基于重力场特征参数信息熵的适配区选择方法

马越原1,2，欧阳永忠1,2，黄谟涛2，邓凯亮2，曲政豪1

（1. 信息工程大学 地理空间信息学院，郑州 450052；2. 海军海洋测绘研究所，天津 300061）

针对当前重力统计特征参数类别繁多，选择标准复杂而导致错选有效匹配区域的问题，利用信息熵具有能够整合多种统计参数且算法计算量小的特点，提出了一种基于特征参数信息熵的重力辅助导航适配区的选择方法。首先，在 DTU10模型下将该方法与传统单一特征参数的方法进行比较，确定了传统方法的确会错误选择可匹配区，从而也反映了所提出方法的优越性；其次，在该方法划分出的匹配区和非匹配区中分别设计了8条仿真航线，匹配区中仿真航线的匹配效果明显优于非匹配区中的匹配效果。仿真结果表明了该方法的有效性。

重力匹配导航；特征统计参数；适配区；重力场信息熵；选择标准

当今，为了提高水下航行器的生存能力，世界上主要海洋强国都在大力发展水下精密导航技术，特别是重力辅助导航技术，更是当前国内外研究的热门课题之一[1]，因为重力匹配导航具有不向外界辐射信号，不易受外界干扰等优点，有较强的自主性[2-3]。但是，其匹配精度是否符合具体航行要求与其进行匹配的区域重力特征是否丰富有极大的相关性。

目前，已经有学者针对陆地重力场统计特征参数进行计算分析[4-5]，并取得了重要研究成果。在海洋重力场的统计分析方面，已有专家提出基于单一重力统计特征参数的适配区选择准则[6-8]，但是所提出的统计参数繁多，除传统使用的重力场标准差、粗糙度、相关系数和坡度等指标外，还有相关峰尖锐性指标、可跟踪度指标、特征密度指标等等。此时，适配区的选择就要同时利用多个参数来进行分析比较，并没有一个综合有效的选择标准。而信息熵具有能够整合多种统计参数的特点，且算法计算量小，有利于简化适配区选择时所需的繁多的参数指标。为此，本文基于DTU10模型下 1′×1′的卫星测高重力异常数据，应用ICCP算法在指定范围内进行模拟仿真试验，验证了所提出的基于重力场特征参数信息熵的适配区选择方法及相关理论的正确性以及在用于适配区域选择时的可行性，达到了简化适配区选择标准的目标。

1 重力场特征分析和适配区选择方法

1.1 重力特征统计参数的定义

重力场的适配统计参数对于描述重力场特征，研究重力匹配区域的选择方法和准则以及重力场特征与捕获概率、定位精度之间的联系具有十分重要的意义。

重力场数据一般都采用格网矩阵的方式存储，设某重力场区域的经纬度跨度为M×N网格，g（i, j）为其中网格点坐标（i,j）处的重力异常值。为了分析局部重力场的统计特征，定义了大小为m×n的局部计算窗口，用来计算局部重力场的各个统计参数。

本文参照地形特征参数来定义重力场特征统计参数[9-11]。

1）重力场标准差指标

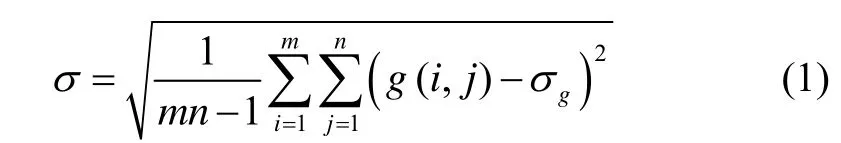
式中：σg是全图重力异常均值，

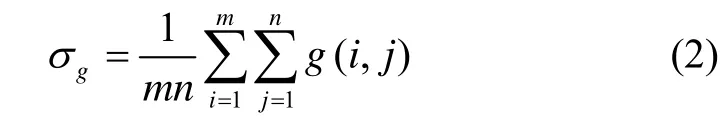
标准差σ是反映重力基准图中重力异常值元素的离散程度和整个重力场总的变化程度的一个尺度。当g(i,j)比较发散时，σ较大；反之，当g(i,j)比较集中时，σ较小。

2）重力场粗糙度指标

重力场粗糙度分为经度方向的绝对粗糙度rλ和纬度方向的绝对粗糙度rφ。

粗糙度是用来描述一个单元内重力场变化，是局部区域重力趋势面的平均光滑程度，能够刻画较细微的局部起伏，其值越大，说明局部重力场变化越明显。

3）重力场相关系数指标

重力场相关系数分为经度方向的相关系数Rλ和纬度方向的相关系数Rφ。

相关系数Rλ和Rφ所反映的是相邻网格点的重力异常值的线性相关程度。当Rλ和Rφ较大时，相邻网格点的相关程度大，重力异常变化较小，不适合匹配；反之，适合匹配。

4）重力场坡度指标

重力场坡度分为经度方向的重力场坡度Sλ和纬度方向的重力场坡度Sφ，重力场坡度Sλ和Sφ反映重力在经度和纬度方向上变化的快慢。

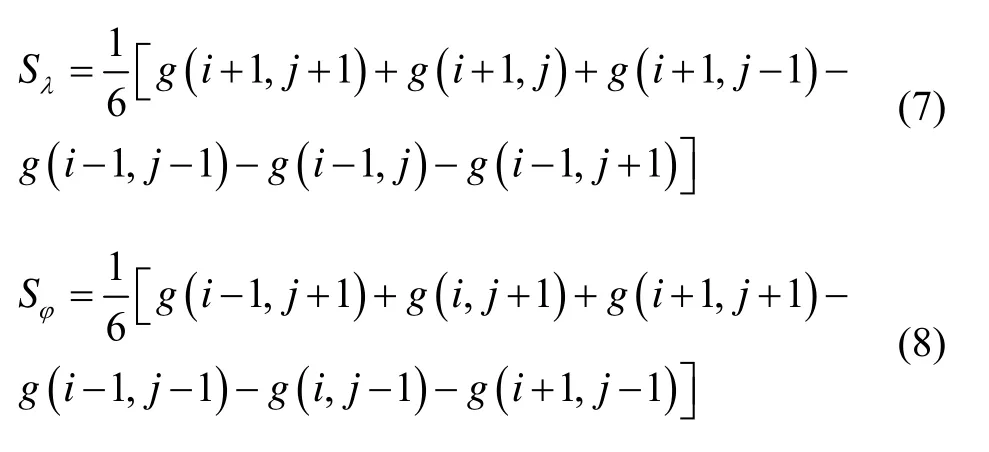
1.2 特征参数计算与分析

为说明以上特征参数所反映的重力场特征，利用400×400个基于DTU10模型下1′×1′的重力异常网格数据，绘出该范围内的重力等值线图，如图1所示，单位为毫伽。表1中所反映的是该区域的部分数值指标。

图1 重力异常分布图Fig.1 Distribution of gravity anomaly

表1 数值指标Tab.1 Numerical results

由式(1)(3)(4)可知，标准差反映了重力异常格网数据的离散程度和整个区域总的起伏程度，粗糙度反映的是整个区域的平均光滑程度。通过编程计算，绘制出标准差图2、经纬度方向粗糙度图3(a)和3(b)。由绘制结果可以看出：这三种统计参数的图形都反映了区域的重力异常数据变化，且趋势一致，即重力异常变化越大，相应区域的重力统计参数值也就越大。

图2表示重力异常标准差填色等值线图，单位为毫伽。数值大小是和重力场特征对应的，特征丰富的区域标准差数值大，特征模糊的区域标准差数值小，因此可以作为衡量重力场特征丰富程度的数量指标。

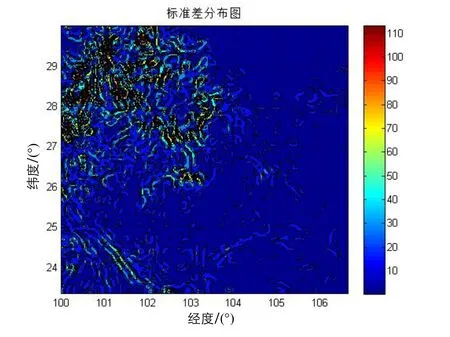
图2 重力场标准差Fig.2 Color-filled contour of standard deviation

图3(a)、图3(b)分别表示了重力场经度和纬度方向的绝对粗糙度填色等值线图，单位为毫伽。从图 3中可以看出，有些区域的重力场特征仅仅在某个方向上较为明显，表现在标准差较大的区域只在经度方向上或纬度方向上粗糙度较大，另一个方向则比较小。因而重力场的这个特点使得在进行匹配导航的时候，匹配算法在经度位置和纬度位置上的匹配效果不同，在哪个方向上的粗糙度大，匹配效果就好，反之，匹配效果就差。限于篇幅，其他统计特征就不一一赘述。

由以上分析可知，用来进行可导航性分析的特征参数非常多，这些统计参数也的确能在不同方面反映重力场分布与匹配成功概率的部分关系，但是，这些参数都有其局限性，即只能反映一个方面的重力场特征。因此用某一个统计参数来表现重力场区域的可匹配性是远远不够的，在应用于实际分析区域可匹配性时，往往要同时用多个参数来进行比较和分析。目前参数的选择没有一个具体的标准，只有通过大量的试验来获得统计标准，但由于选择过多，容易因为参数的差异导致选择错误的区域。

图3(a) 重力场经度方向绝对粗糙度Fig.3(a) Absolute roughness in longitude direction

图3(b) 重力场纬度方向绝对粗糙度Fig.3(b) Absolute roughness in longitude direction

2 基于信息熵的适配区选择方法

为了解决上述问题，可以利用信息熵进行可匹配区的选择，其计算公式为[12-13]

式中：I为信息量； p(xi)表示事件xi出现的概率；对数的底a决定信息量的单位，一般取a=2，单位为比特（bit）。

上述方法仅用重力场信息熵一个参数，即可对区域的可匹配性进行分析，但是在体现重力场特征方面不够全面。根据可匹配区划分的基本原则，完善的重力场可匹配区划分标准，应该要同时反映重力场区域的相对变化和绝对变化，且形式简单明了。因而本文借鉴两种方法的优点，总结出一种基于“重力场特征参数信息熵”的可匹配区划分方法，下面介绍其具体原理。

根据重力场特征参数的定义，经度粗糙度rλ反映了重力场数据在经度方向的变化，相应的纬度粗糙度rφ反映的是纬度方向的变化。取经向和纬向的总体粗糙度rφλ为二者之和，即rφλ=rφ+rλ，则经向粗糙度rλ与总体粗糙度rφλ的比值为经向粗糙度出现的概率，即为纬向粗糙度rφ与总体粗糙度rφλ的比值为纬向粗糙度出现的概率，即为根据两种粗糙度并顾及信息熵的定义，可以求解两种粗糙度的熵：

粗糙度的熵值可以均衡地体现重力场在两个方向上的变化，例如某区域中，重力场仅仅在纬度方向变化大，而在经度方向变化小，此时的熵值会非常小，若使熵值变大，重力场需要在两个方向上均衡变化。因而，根据粗糙度熵值的大小，可观察区域重力场在两个方向上的变化：熵值越大重力场变化越均衡，潜在的可匹配性能就越好，反之就越差。但是熵值只能体现重力场的相对变化，有可能某区域的重力场在两个方向的绝对变化都非常小，但由于变化较为均衡，此时该区域的重力场熵值也有可能很大。要想全面反映区域的重力场变化，重力场熵值还应该要能反映区域的绝对重力场变化，而重力场特征参数中的标准差σ正是这一指标的反映，把两种参数结合在一起就能较好的体现重力场变化的特征。

根据上述分析，给出网格点坐标为(i,j)处的重力场特征参数信息熵的公式如下：

图4 区域重力场特征参数信息熵图Fig.4 Information entropy of gravity characteristic parameter

当统计窗口在整个区域全部网格点上移动一遍之后，就能得到整个重力场区域的重力场特征参数信息熵。以图1区域的重力异常数据为例，计算的重力场特征参数信息熵值如图4所示。

熵的最大值为88.266，最小值为0。由图4的熵值3D图，可了解区域重力场变化的基本特征：特征参数信息熵值越大的地方，重力场起伏也越大。

3 仿真实验

3.1 与单一统计特征参数划分匹配区效果的比较

前面已经提到，只利用单一统计参数容易选择错误的可匹配区域，这里我们用标准差和信息熵所划分的可匹配区的差异对比来进行验证。根据计算的标准差和特征参数信息熵值，设定一个阈值0～25，在这区间的区域重力场变化十分不明显，不利于重力匹配导航的实施。阈值的选定视实际情况而定。如图5(a)和图5(b)中白色区域可以看出：该研究区域有超一半海域的熵值在25以下；而在25以上的区域分布较集中，在这些区域实施重力匹配导航时，比较容易实现。可以看出，在北纬24.5°～25°，东经100°～101°范围内，利用标准差所划分的匹配区是显示可匹配的，而利用特征参数信息熵所划分的可匹配区显示不可匹配。为了验证其正确性，我们在这个范围内设计一条航迹，利用ICCP算法进行匹配，所得结果如图6。

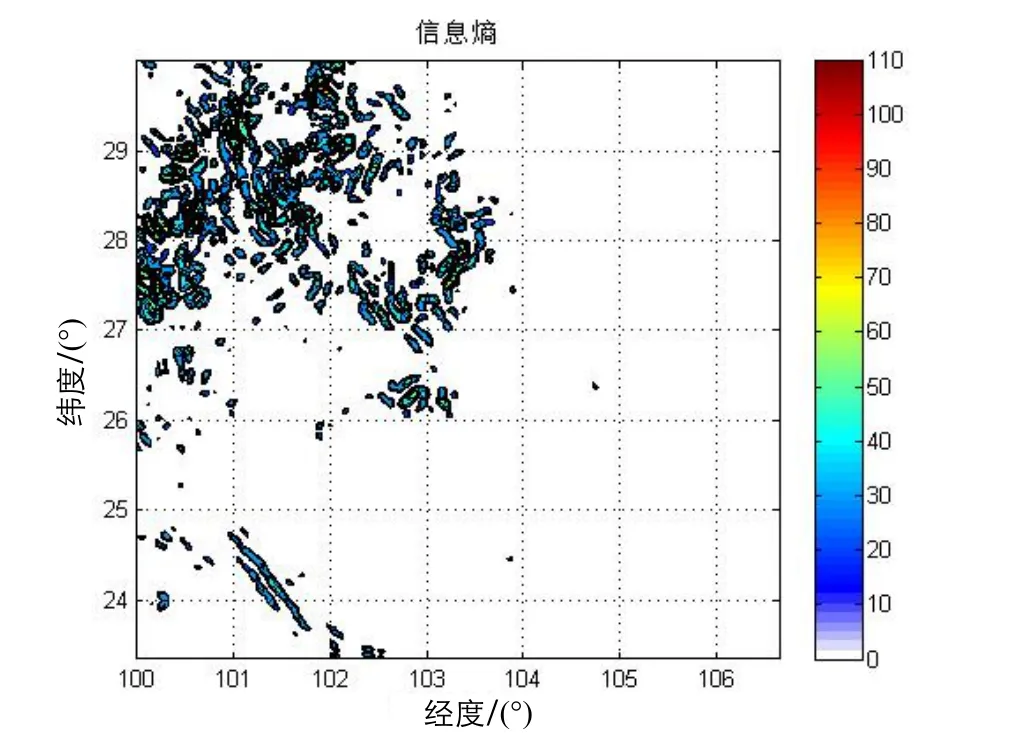
图5(b) 信息熵可匹配区分布Fig.5(b) Matching region distribution of entropy

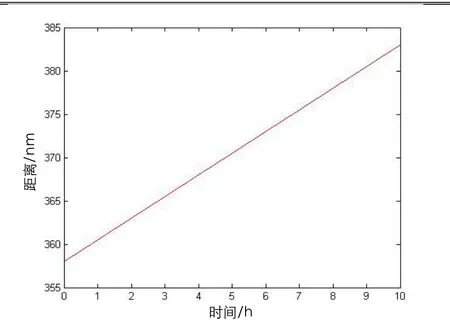
图6 匹配航迹与真实航迹的距离变化Fig.6 Distance between matching track and real track

从图6中可以看出，匹配航迹与真实航迹之间的距离随着时间的变化呈发散趋势，说明在此区域内匹配效果并不好。

由此可见，只利用单一统计参数有可能会错误选择可匹配区，从而也反映出基于特征参数信息熵在划分可匹配区的优越性。

按照重力场特征参数信息熵这种划分可匹配区的方法，只用一个参数即可反映区域重力场的变化，比用多种特征参数分析更简便，也能避免选择错误的可匹配区。与此方法类似，还可以在式(10)中引入相关系数、重力坡度等其他统计量，根据具体实验条件和要求，来得到更加精确更加可靠的匹配区域。

3.2 匹配区航迹仿真

为了验证基于特征信息熵划分匹配区的方法的可用性，我们在图5(b)中所划出的可匹配区和非可匹配区分别设计了16组实验航线，其中8组航线穿过特征信息熵平缓变化地区，即第3.1节划定的不可匹配区，8组穿过可匹配区。仿真所有匹配航迹均由ICCP算法进行匹配计算，得到每组航线的匹配轨迹和真实轨迹间距离变化的RMS值[14-15]见表2。图7(a)和图7(b)所示为其中一组实验航线的仿真轨迹。

从表2和图7(a)和图7(b)中可以看出，匹配区中的仿真航线匹配效果明显优于非匹配区中仿真航线的匹配效果。

表2 航迹仿真结果Tab.2 Simulation results of tracks

图7(a) 匹配区航迹仿真Fig.7(a) Simulation on tracks in matching area

图7(b) 非匹配区航迹仿真Fig.7(b) Simulation on tracks in non-matching area

4 结束语

通过以上实验可以得出以下结论：利用重力场特征信息熵对重力场区域的可匹配性进行分析是可行的。通过特征信息熵得出可匹配区，在可匹配区的区域范围内进行匹配，可有效改进重力辅助导航技术的应用效果。

（References）：

[1] Anonsen K B, Hagen O K. An analysis of real-time terrain aided navigation results from a HUGIN AUV[C]// OCEANS 2010. Seattle: IEEE, 2010: 1-9.

[2] 李姗姗. 水下重力辅助惯性导航的理论与方法研究[D].郑州: 解放军信息工程大学, 2010. Li Shan-shan. Research on the theory and method of underwater gravity-aided inertial navigation[D]. Zhengzhou: The PLA Information Engineering University, 2010.

[3] Liu M, Chang G. Gravity matching aided inertial navigation technique based on marginal robust unscented Kalman filter[J]. Mathematical Problems in Engineering, 2015: 1-9.

[4] 李姗姗, 吴晓平, 张传定, 等. 我国重力场新的统计特征参数的计算分析[J]. 地球物理学报, 2010, 53(5): 1099-1108. Li Shan-shan, Wu Xiao-ping, Zhang Chuan-ding, et al. Calculation and analysis of the new statistical character parameters of gravity field in China[J]. Chinese Journal of Geophysics, 2010, 53(5): 1099-1108.

[5] Zhu Zhuang-sheng, Guo Yi-yang, Yang Zhen-li. Study on initial gravity map matching technique based on triangle constraint model[J]. Journal of Navigation, 2016, 69: 353-372.

[6] Capozziello S, De Laurentis M, Odintsov S D. Hamiltonian dynamics and Noether symmetries in Extended Gravity Cosmology[J]. The European Physical Journal C, 2012, 27(7): 1-21.

[7] 蔡体菁, 陈鑫巍. 基于层次分析法的重力匹配区域选择准则[J]. 中国惯性技术学报, 2013, 21(1): 93-96. Cai Ti-jing, Chen Xin-wei. Selection criterion based on analytic hierarchy process for matching region in gravity aided INS[J]. Journal of Chinese Inertial Technology, 2013, 21(1): 93-96.

[8] Deng Zhong-liang, Ge Yue-tao, Guan Wei-guo, et al. Underwater map-matching aided inertial navigation system based on multi-geophysical information[J]. Frontiers of Electrical and Electronic Engineering, 2010, 5(4): 496-500.

[9] 郑彤, 蔡龙飞, 王志刚, 等. 地形匹配辅助导航中匹配区域的选择[J]. 中国惯性技术学报, 2009, 17(2): 191-196. Zheng Tong, Cai Long-fei, Wang Zhi-gang, et al. Selection of matching area in terrain match aided navigation[J]. Journal of Chinese Inertial Technology, 2009, 17(2): 191-196.

[10] 饶喆, 张静远, 冯炜. 一种地形匹配导航区域的可导航性评价[J]. 河南大学学报(自然科学版), 2016, 46(1): 89-95. Rao Zhe, Zhang Jing-yuan, Feng Wei. Navigability evaluation method of terrain matching navigation area[J]. Journal of Henan University (Natural Science), 2016, 46(1): 89-95.

[11] Hou S Y, Hung H S, Chang S H, et al. Novel algorithm for tracking multiple targets[J]. Journal of Marine Science and Technology, 2010, 18(2): 259-267.

[12] Santos A C S, Pedrini H. A combination of k-means clustering and entropy filtering for band selection and classification in hyperspectral images[J]. International Journal of Remote Sensing, 2016, 37(13): 3005-3020.

[13] 徐晓苏, 汤郡郡, 张涛, 等. 基于熵值法赋权灰色关联决策的地形辅助导航适配区选择[J]. 中国惯性技术学报, 2015, 23(2): 201-206. Xu Xiao-su, Tang Jun-jun, Zhang Tao, et al. Selection for matching area in terrain aided navigation based on entropy-weighted grey correlation decision-making[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 201-206.

[14] 谌剑, 张静远, 李恒, 等. 基于灰色决策的地形辅助导航区域选取方法[J]. 海军工程大学学报, 2012, 24(5): 48-53. Shen Jian, Zhang Jing-yuan, Li Heng, et al. An underwater terrain matching arithmetic based on particle filter [J]. Journal of Naval University of Engineering, 2012, 24(5): 48-53.

[15] Zhou J M, Ju Z W. Multi-elements decision-making method based on grey decision model and analytic hierarchy process[C]//2011 International Conference on Remote Sensing, Environment and Transportation Engineering. 2011: 3288-3291.

Selection method for gravity-field matchable area based on information entropy of characteristic parameters

MA Yue-yuan1,2, OUYANG Yong-zhong1,2, HUANG Mo-tao2, DENG Kai-liang2, QU Zheng-hao1
(1. Institute of Geospacial Information, Information Engineering University, Zhengzhou 450001, China; 2. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China)

At present, there are a variety of characteristic parameters in gravity statistics, whose selection criteria are complex and can lead to incorrectly matching the effective area. To solve this problem, a selection method for gravity-aided navigation adaptation area is proposed based on the information entropy of characteristic parameters which can integrate a variety of statistical parameters and is low in calculation amount. Based on DTU10 model, comparison is made between the proposed method and the traditional method with single characteristic parameter, which proves that that traditional method may incorrectly choose the matching area, while the proposed method has not this disadvantage. The proposed method divide the gravity field into matching area and the non-matching area, and 8 simulation tracks are designed on either of the areas. Simulation results show the feasibility and effectiveness of the proposed method.

gravity matching navigation; characteristic statistical parameter; matching area; gravity field information entropy; selection standard

U666.1

：A

2016-09-07；

：2016-11-25

国家自然科学基金项目（41474012）；国家重大科学仪器设备开发专项资助项目（2011YQ12004503）；国防 973计划资助项目（613219）

马越原（1991—），男，工程师，从事重力辅助导航研究。E-mail: myy15c@126.com

联 系 人：欧阳永忠（1969—），男，高级工程师，博士生导师。E-mail: ouyangyz@sohu.com

1005-6734(2016)06-0763-06

10.13695/j.cnki.12-1222/o3.2016.06.012