一种新型的GPS弱信号精捕获方法
2016-04-15缪玲娟郭岩冰邵海俊石永生
张 希,缪玲娟,郭岩冰,邵海俊,石永生
(北京理工大学 自动化学院,北京 100081)
一种新型的GPS弱信号精捕获方法
张 希,缪玲娟,郭岩冰,邵海俊,石永生
(北京理工大学 自动化学院,北京 100081)
为提高GPS接收机在低信噪比环境中的捕获精度和灵敏度,提出了一种新的弱信号精捕获算法。该算法采用差分相干积分缓解平方损耗,并利用积分结果的相位信息修正载波频率,使其估计精度不再受到频移搜索步长的限制。此外,该算法根据载波多普勒和码多普勒的比例关系,直接对本地码相位进行校正,保证了信号积累时间较长时不同相关峰之间的重叠性,有助于提高捕获灵敏度并能够得到接收信号末端精确的码相位。仿真结果表明,载波频率和码相位的估计误差分别小于20 Hz和1个采样点,在给定的信号积累时间下,本地码相位校正对捕获灵敏度的提升可达3.2 dB。
GPS信号捕获;差分相干积分;频率修正;本地码相位修正;弱信号
1 差分相干积分的噪声特性分析
对于软件接收机而言,由射频前端获得的实数型中频信号可以表示为

式中:输入信号u(t)的平均功率为a2,D(t)为导航电文数据比特,c(·)为调制载波的 CA码,η为码多普勒频移因子,f和θ则分别为接收信号的载波频率和初相位,n(t)代表均值为零、方差为σ的高斯白噪声。同时,本地正弦载波复制信号可以表示为

式中:f′和θ′分别为u′(t)的频率和初相位。将u(t)和u′(t)两者混频相乘并忽略高频成分,得到简化后的乘积为

式中:fe=f-f′,θe=θ-θ′,并且噪声量ni(t)的方差仍旧维持在
本文算法以差分相干积分为基础,为分析其噪声特性,将i(t)与本地CA码ck(t)进行相关,其结果在tk至tk+Tcoh(Tcoh为相干积分时间)时段上的积分可以表示为

式中:

类似地,正交支路在该时段,以及同相、正交支路在下一时段,即tk+1至 tk+1+Tcoh时段相关结果的积分,可分别表示为,以及进一步,将这两个相邻时段复数形式的积分结果共轭相乘,可以得到:

式中:

考虑到Ik、Qk与Ik+1、Qk+1均不相关,并且有用信号与噪声也互不相关,自然有:
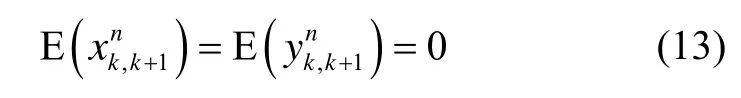
即差分相干积分不会带来均值不为零的噪声。
另一方面,同样是因为有用信号与噪声的不相关性,差分相干积分与传统非相干积分噪声的不同可表示为


可以得到:而考虑到噪声的随机性,式(16)“≤”中的等号几乎不可能取到。

以上分析表明,差分相干积分利用相邻两个相干结果的不相关性,避免了带来不易被积分器滤除的噪声,从而在根源上缓解了平方损耗。因此,在积累时间相同的前提下,差分相干积分具有比传统非相干积分更好的噪声抑制能力。
2 基于差分相干积分的频率修正
通常情况下,只要信号积累结果的幅值大于预先设定的检测门限,即可认为接收机成功捕获到了GPS信号。此时,载波多普勒频移的捕获精度仅由频移搜索步长决定。而本节通过保留差分相干积分结果的相位信息,能够对捕获到的载波多普勒频移加以修正。
首先,假设数据比特D(t)在tk至tk+Tcoh期间不发生跳变,则式(5)可以展开为

式中:Δτk为码相位误差;R(·)为CA码的自相关函数,并且数据比特由D(t)在积分时段内的第一个采样点处的值D表示。此处先假设Δτk可以忽略不计,则式(17)可以进一步简化为


式中,N是参与累加的共轭相乘结果总数。观察由式(22)表示的信号积累结果可以发现其辐角不随时间变化,故可利用式(22)本身对载波多普勒频移的估计值进行修正。对于常见的频移搜索范围-5 kHz~5 kHz,搜索步长通常设置为500 Hz,则在含有GPS信号的搜索单元,fe最大为250 Hz。此时,若设置Tcoh为一个标称的CA码周期即1ms,则显然有:
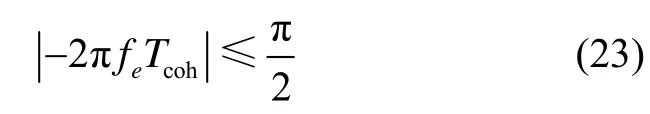
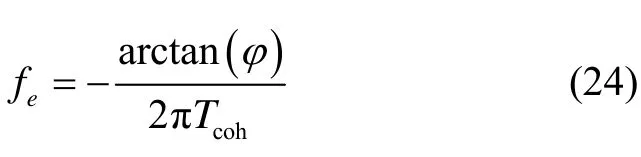
此时,将峰值所对应的搜索频点与fe相加,即可得到精度不受步长限制的载波多普勒频移估计值。
3 本地码相位校正及本文算法流程
当Tcoh为1 ms时,每二十个相邻的共轭相乘结果中,最多有一个会受到导航电文数据比特跳变的影响,可以认为20 ms的数据比特宽度对信号积累时间的限制已被打破。因此,上一节通过累加多个共轭相乘结果进行长时间的信号积累,以提高接收机的捕获灵敏度。
然而,在传统的捕获算法中,与不同时段的接收信号进行相关的本地CA码通常有着相同的相位,即ck(t)=c(t)。在这种情况下,由于码多普勒的存在,接收信号与本地信号的码相位将会发生相对滑动。随着时间的推移,式(17)中的码相位误差Δτk将逐渐变大,直至无法忽略不计。也即当进行累加的共轭相乘结果个数较多时,接收信号与本地信号之间的码相位滑动将对信号积累的效果造成显著的不良影响。
因此,本节设置ck(t)为c(t+τk),并且


考虑到频移搜索步长,可知至少需要616 ms,码相位误差Δτk才会大于 0.1码片,即经过本地码相位校正后,由式(17)至式(18)所做的简化才较为合理。
在离散形式下,这种校正可以通过对参与t1至t1+Tcoh时段相干积分的本地CA码c1进行移位来具体实现。根据式(25),可将码相位校正量以采样点个数的形式表示:

式中:fs为采样频率。显然,在当前载波搜索频点大于零时,有Nk>0。此时,将c1向左循环移动Nk位即可得到ck,反之,当Nk<0时,c1则应向右循环移位。在这种实现方式下,最终接收机捕获得到的峰值码相位即是接收信号起始端的码相位。
至此,可将本文提出的新型GPS弱信号精捕获算法流程绘于图1,并简述如下:
① 接收由射频前端获得的数字中频信号,并按设置好的搜索频点对其进行载波剥离;
② 对本地CA码相位进行校正,并利用快速傅里叶变换(Fast Fourier Transform,FFT)技术实现其与接收信号的并行处理[11]:
③ 将相邻的相干积分结果共轭相乘后依次累加;
④ 如果最大差分相干结果小于检测阈值,则在下一个载波搜索频点重新搜索;
⑤ 若成功捕获到信号,则根据式(24)修正载波多普勒频移估计值,同时,由式(27)及峰值的码相位推算得到信号末端的码相位。

图1 GPS弱信号精捕获算法流程Fig.1 Schematic of the proposed acquisition method
4 仿真验证
在GPS的实际应用中,处于室内等低信噪比环境中的接收机通常要面对复杂的噪声条件,甚至可能由于建筑物等的遮挡,使得接收机天线根本无法接收到卫星信号。因此,本文利用采样率为16.368 MHz的射频前端在开阔地带(N:39°57′36.16″,E:116°19′1.58″,Hgt:32.9 m)接收GPS信号(接收功率大于-128 dBm,即SNR大于-18 dB),然后在其基础上人为叠加不同强度的随机噪声,从而仿真生成了不同信噪比(SNR应小于-35 dB才属于弱信号范畴)的中频信号。为便于分析本文算法的有效性,选取PRN25和PRN18两颗卫星,其载波多普勒频移和码相位的参考值,可由接收机跟踪原始强信号得到:
PRN25,载波多普勒频移为314 Hz,在300 ms内,码相位保持为第8610个采样点;
PRN18,载波多普勒频移为4378 Hz,在300 ms内,码相位由第3058个采样点滑动至第3045个采样点。
4.1 差分相干积分及频率修正的效果检验
以PRN25为例,图2描述了非相干积分、差分相干积分在总的信号积累时间T分别为100 ms和300 ms时,在不同信噪比下执行1000次蒙特卡洛仿真的检测概率比较结果,其中NCH表示非相干积分,DCH表示差分相干积分。显然,差分相干积分对噪声的抑制能力更好,在90%的检测概率下,可以使接收机的灵敏度提升1.6 dB左右。从图2中还可得知,延长T可以使两种方法的处理增益均提高2.8 dB左右。另外,值得说明的是,由于PRN25载波多普勒较小,接收信号在300 ms内的码相位滑动可以忽略不计,所以此处并未对本地码相位进行校正。
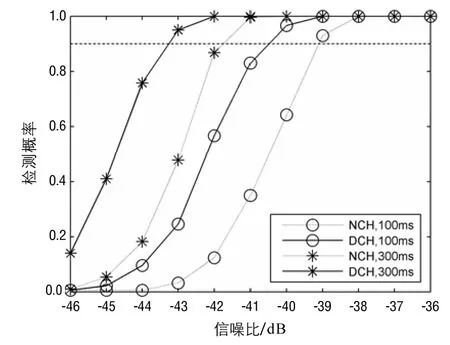
图2 非相干积分和差分相干积分的检测性能比较Fig.2 Detection performance of non-coherent integration and differentially coherent integration
图3给出了成功捕获到GPS信号后,利用式(24)校正得到的载波多普勒频移估计值的均方根误差。可以看到,当采用较长的信号积累时间时,载波多普勒频移的校正精度相对较高,这是因为此时相关峰值相对于噪声基底更大,辐角的计算更不易受到噪声的影响。结合图2分析可知,当检测概率大于90%时,在两种信号积累时间下,载波多普勒频移估计值的均方根误差均小于 20 Hz,即载波多普勒频移捕获的精度大幅提升,不再受到频移搜索步长的限制。

图3 载波多普勒频移估计值的均方根误差Fig.3 Root-mean-square errors of Doppler shift estimates
4.2 本地码相位校正的效果检验
对于 PRN18,由于其载波多普勒频移较大,在较长的信号积累时间下,码相位的滑动会相对明显。为证明这一点,设置PRN18的信噪比为-33 dB,利用300 ms的接收信号和固定的本地CA码,依次进行15次20 ms的差分相干积分。在4.5 kHz这一搜索频点处,所有的相关峰如图4(a)所示,显然,它们并不重叠。当进行300 ms的差分相干积分,即叠加这15个相关峰时,自然无法达到理想的信号积累效果。图 4(b)则给出了进行本地码相位校正后的相关峰分布,可以看到,这些相关峰对应的码相位均为第3058个采样点,即本文算法能够保证进行长时间信号积累时相关峰的重叠性。
此外,根据式(27)可知,进行最后一次相干积分时,本地码相位的校正量为13个采样点,所以能够推算出接收信号末端的码相位为第3045个采样点。而不进行本地码相位校正时,仅能得知300 ms差分相干积分结果的峰值位于第3052个采样点。与PRN18原始强信号的跟踪结果进行比较后可以发现,采用本文算法可以使码相位的捕获结果更为准确。


图4 相关峰的分布Fig.4 Distribution of correlative peaks
仍旧以PRN18为例,图5描述了差分相干积分以及本文算法在T分别为100 ms、300 ms和600 ms时,在不同信噪比下运行1000次蒙特卡洛仿真的检测概率比较结果,其中CDCH表示带本地码相位校正的差分相干积分。显然,在90%的检测概率下,如果不对本地码相位进行校正,将T从100 ms延长至300 ms,接收机处理增益仅能提高1.5 dB左右。结合图4(a)分析可知,随着时间的推移,接收信号CA码相位的滑动甚至会逐渐超过1码片,此时一味地继续延长T将没有任何意义。另一方面,在对本地码相位进行校正后,延长T至300 ms,则可以使接收机处理增益提高2.8 dB,这与图2中接收信号码相位滑动可以忽略不计时的结果一致。此外,从图5中还可以看到,当T为600 ms时,本地码相位校正对捕获灵敏度的改善已达3.2 dB,即T越大,采用本地码相位校正的优势就越为明显。

图5 本地码相位校正对捕获灵敏度的改善Fig.5 Effect of local code-phase correction on promoting acquisition sensitivity
5 结 论
由于差分相干积分具有良好的噪声抑制能力,本文以其为基础设计了一种新型的 GPS弱信号精捕获算法。通过保留差分相干积分结果的相位信息,该算法能够大幅提高载波多普勒频移的估计精度,使其不再受到频移搜索步长的限制。同时,该算法通过对本地CA码进行循环移位,保证了长时间的信号积累不受接收信号码相位滑动的不良影响。
仿真结果表明,接收信号载波多普勒越大,总的信号积累时间越长,这种对本地码相位进行校正的方法对接收机捕获灵敏度的提升也就越为明显。此外,该方法能够获得信号末端精确的码相位,有利于接收机准确地设置后续跟踪环节的初值。
(References):
[1] 袁建国, 欧松林, 刘飞龙, 等. 一种适用于微弱信号的新颖双峰值比率捕获策略[J]. 中国惯性技术学报, 2015, 23(1): 98-102. Yuan Jian-guo, Ou Song-lin, Liu Fei-long, et al. Novel double peak value ratio acquisition strategy for weak signal[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 98-102.
[2] Kovar P, Kacmarik P, Vejrazka F. Interoperable GPS, GLONASS and Galileo software receiver[J]. IEEE Aerospace and Electronic Systems Magazine, 2011, 26(4): 24-30.
[3] O'Driscoll C, Petovello M, Lachapelle G. Software receiver strategies for the acquisition and re-acquisition of weak GPS signals[C]//Proceedings of the Institute of Navigation, National Technical Meeting. California, 2008: 843-854.
[4] 李寅寅, 徐晓苏, 刘锡祥. 基于半比特交替和FFT组合的GPS软件接收机弱信号捕获算法[J]. 中国惯性技术学报, 2012, 20(1): 46-50. Li Yin-yin, Xu Xiao-su, Liu Xi-xiang. Acquisition algorithm based on half-bit alternation and FFT combination for weak signals of GPS software receiver[J]. Journal of Chinese Inertial Technology, 2012, 20(1): 46-50.
[5] Ma Jing-wei, Miao Ling-juan, Zhang Xi, et al. Weak signal acquisition algorithm of GPS software receiver aided by INS[C]//Sixth International Symposium on Computational Intelligence and Design. Hangzhou, China, 2013: 321-325.
[6] Borio D, O'Driscoll C, Lachapelle G. Coherent, noncoherent, and differentially coherent combining techniques for acquisition of new composite GNSS signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 1227-1240.
[7] Ta T H, Qaisar S, Dempster A G, Dovis F. Partial differential postcorrelation processing for GPS L2C signal acquisition[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1287-1305.
[8] 黄新明, 龚航, 朱祥维, 等. GNSS信号捕获中的伪码多普勒补偿技术[J]. 中南大学学报(自然科学版), 2015, 46(6): 2134-2141. Huang Xin-ming, Gong Hang, Zhu Xiang-wei, et al. Code Doppler compensation method for GNSS signal acquisition[J]. Journal of Central South University (Science and Technology), 2015, 46(6): 2134-2141.
[9] 黄仰博. 高性能导航接收机基带处理算法与实现技术研究[D]. 国防科学技术大学, 2011. Huang Yang-bo. Baseband algorithms and implementation tech. for high-performance navigation receiver[D]. National University of Defense Technology, 2011.
[10] Jafarnia A. GNSS signal authenticity verification in the presence of structural interference[D]. University of Calgary, 2013.
[11] Babu S R, Selvam P, Rao G S, et al. Optimization of GPS L1 acquisition using Radix-4 FFT[C]//International Conference on Recent Trends in Information Technology. 2011: 875-879.
Novel fine acquisition method for weak GPS signal
ZHANG Xi, MIAO Ling-juan, GUO Yan-bing, SHAO Hai-jun, SHI Yong-sheng
(School of Automation, Beijing Institute of Technology, Beijing 100081, China)
To improve the acquisition accuracy and sensitivity of GPS receiver in low signal-to-noise ratio (SNR) environment, a new kind of acquisition method for weak signal is proposed. This method makes use of differential coherent integration to reduce power loss, and breaks the restriction of searching step size on the estimation accuracy of carrier Doppler shift by utilizing the phase information of integration results. Moreover, based on the relationship between carrier and code Doppler shifts, this method can directly amends the local code phase. As a result, it ensures different correlation peaks’ overlap with each other and can obtain accurate code phase of the received signal. Simulation results show that the estimation errors of carrier Doppler shift and code phase can be kept to less than 20 Hz and one sampling point respectively, and , in a given case, the acquisition sensitivity is improved by about 3.2 dB.
GPS signal acquisition; differential coherent integration; frequency correction; local code phase correction; weak signal
U666.1
:A
2016-08-24;
:2016-09-09
国家自然科学基金(61473039)
张希(1989—),男,博士研究生,从事卫星导航和组合导航研究。E-mail: zhangx_lancer@sina.com
作者简介:缪玲娟(1965—),女,教授,博士生导师。E-mail: miaolingjuan@bit.edu.cn
1005-6734(2016)06-0752-06
10.13695/j.cnki.12-1222/o3.2016.06.010
收稿日期:2016-09-11;修回日期:2016-11-20
基金项目:国家自然科学基金项目(61273049);陕西省自然科学基金(2014JM8309)
作者简介:伍劭实(1990—),男,博士研究生,主要研究方向为卫星导航与定位。E-mail: wushaoshipaper@163.com
联 系 人:庞春雷(1986—),男,讲师。Email: chunleipcl@163.com
全球定位系统(Global Positioning System,GPS)能够实现全球、全天候的高精度导航,并且具有定位、定速误差不随时间发散的特性,已成为一种被广泛应用的重要导航技术。但由于涉及外部信号的接收,在城市低谷、室内等低信噪比(Signal-to-Noise Ratio,SNR)环境下,普通的GPS接收机便有可能无法捕获功率较弱的卫星信号,接收机的后续功能,如信号跟踪、电文提取、导航解算等,也将无从谈起。 近年来,随着软件接收机的飞速发展,弱信号处理算法的验证过程得到了极大的简化,高灵敏度的GPS信号捕获技术也因此逐渐成为了GPS应用领域的研究热点[1-2]。
一般而言,为提高GPS接收机的处理增益,最有效的方法是增加信号的积累时间。但由于卫星导航电文数据比特每20 ms即可能发生翻转,正负相消的相关结果会严重影响相干积累的检测值,所以在捕获阶段信号的相干积分时间通常不超过10 ms[3]。虽然在确定数据比特的起始位置后,可以将相干积分时间进一步延长以获得更高的信噪比,但这却意味着迅速增长的计算复杂度[4-5]。另一种常见的信号处理方法则是非相干积分。通过将多个相干积分结果平方后相加,该方法能够使信号积累时间大于 20 ms。然而,与噪声功率成正比的平方损耗[6-7]限制了其在低信噪比环境中的应用。另外,由于卫星和接收机之间的相对运动会使信号的码频率发生偏移,采用较长信号积累时间的效果会受到不良影响。为解决这一问题,一种直观的方式是对本地伪码频率进行补偿,但这种方案会改变一个伪码周期对应的采样点数,从而使得一些采用并行处理的捕获算法不易实现[8-9]。针对上述传统算法的缺点,本文提出了一种新的GPS弱信号精捕获算法。
