双导弹拦截角度协同的微分对策制导律
2016-04-15花文华张拥军张金鹏孟庆龄
花文华,张拥军,张金鹏,2,孟庆龄
(1. 中国空空导弹研究院,洛阳 471009;2. 航空制导武器航空科技重点实验室,洛阳 471009)
双导弹拦截角度协同的微分对策制导律
花文华1,张拥军1,张金鹏1,2,孟庆龄1
(1. 中国空空导弹研究院,洛阳 471009;2. 航空制导武器航空科技重点实验室,洛阳 471009)
为提高命中高价值目标的概率,基于线性二次型微分对策理论,对两枚导弹协同拦截单个目标的制导律进行了研究。单枚导弹在最小化自身脱靶量的同时,与另一枚导弹实现拦截角度上的协同,从而构成特定的拦截态势,以提高拦截机动目标的性能和末制导尾端对目标的可观测性。所推导的微分对策制导律考虑到了对策三方的控制系统动态,且具有解析解,形式上为零控脱靶量和零控协同拦截角误差的线性组合。基于推导结果完成了微分对策制导律的制导增益和对策空间分析,给出了鞍点解的存在条件,并进行了分析。非线性系统仿真结果表明由于导弹间存在显式的协同关系,拦截目标所需的加速度较低,且在设定的协同拦截角度收敛后,加速度会进一步减小。
末制导律;微分对策;协同制导;目标拦截
多导弹协同易于构建更加有利的目标拦截态势,从而改进制导性能并降低控制量要求;多弹协同也可用于饱和目标防御,限制目标机动概率,诱骗目标和增强对目标的可观测性等方面[1-3]。导弹协同方式主要包括隐式和显式两种:隐式协同中各导弹是彼此独立的,一种典型情况是多个导弹以不同的终端碰撞角度拦截目标[4-7],从而饱和目标防御;而显式协同则不同,各导弹的弹道是相关的,并围绕着期望的协同关系飞行,这一关系可以为飞行时间[8-9]或其他终端约束,如拦截角度等。显示协同由于考虑到了导弹彼此间的弹道关系,可以获得更好的制导性能。文献[10]针对两枚导弹与单个目标的线性二次型非零和微分对策问题进行了研究,当单枚导弹的脱靶量小于另一枚导弹时,开始执行二对一的对抗策略直到两枚导弹的脱靶量相等。文献[9]给出了一种多弹攻击时间显式协同的制导律,是比例导引的一种衍生形式,实现了多弹对地面固定目标的同时攻击,但不适用于运动目标和机动目标的情况。
本文基于线性二次型微分对策理论,提出一种双导弹拦截角度和脱靶量显式协同的微分对策制导律。
1 问题描述与建模
制导末端两枚导弹和目标的相对运动关系如图 1所示,XI-O-ZI为笛卡尔惯性坐标系,下标P、E分别表示导弹和目标的相关状态,数字1和2对应导弹1和导弹2。图1中z表示导弹和目标之间的相对位移,λ为视线角,导弹航向角采用γ表示,若导弹和目标保持速度不变,则两枚导弹拦截方向的夹角为 γ2-γ1,aP1、aP2和aE分别为导弹1、导弹2和目标的加速度。基于下述假设进行问题的分析:
1) 导弹和目标可视为质点,近似具有一阶控制系统动态特性;
2) 导弹和目标速度大小不变,前者机动能力大于后者;
3) 导弹和目标间的相对运动关系可沿初始视线方向进行线性化。
文献[11]验证了末制导段线性化假设在机动目标拦截上的有效性和可行性,本文还将通过非线性系统仿真对基于上述假设的推导结果进行验证。

图1 平面弹目相对运动关系Fig.1 Planar engagement geometry

式(1)中:

τP1、τP2和 τE分别为导弹1、导弹2和目标的一阶控制系统时间常数,uP1、uP2和uE为对应的控制指令。
基于假设2)和假设3),导弹的飞行时间近似为

式(2)中:ρ0为弹目初始距离,Vc为弹目接近速度。则剩余飞行时间可表示为

式(3)中:t表示当前时间。由于未对剩余飞行时间进行协同设计,两枚导弹在拦截目标的过程中总是存在飞行时间差,假设tgo1<tgo2,导弹1在满足式(4)所示的条件后,认为拦截目标的任务结束:


2 协同微分对策制导律
2.1 性能指标定义和系统降阶
近年来,微分对策理论应用于机动目标拦截方面得到了较为深入的研究[12-16]。对策双方分别追求性能指标的最大化和最小化,微分对策制导律相比最优制导律对目标机动形式及加速度估计误差鲁棒性更强。
定义线性二次型性能指标为

式(6)中:α1,α2,β,η,ηE>0为加权设计参数。α1,α2→∞表示完全拦截情形,脱靶量趋于零;α1,α2<∞时脱靶量为有限非零值;α2,β,η→0时则转化为导弹1和目标间的微分对策问题;η和ηE分别表征了导弹2和目标相对于导弹1的机动能力,当其机动能力较强时,η和ηE取较小值,ηE→∞则表示拦截非机动目标的情形,由假设2),ηE>1。σ为设计的两枚导弹拦截方向的夹角,用于拦截角度的协同。
求解系统方程(1)所对应的奇次微分方程,并经进一步整理可以得到:

式(7)中:

Φ(tf,t )为系统(1)的状态转移矩阵;zP1、zP2和zγ表征了导弹和目标由时间t起零控,并保持该时刻的参数飞行至拦截结束时的脱靶量和协同拦截角度,分别为导弹1的零控脱靶量、导弹2的零控脱靶量和二者的零控协同拦截角。
由式(7)可以得到:
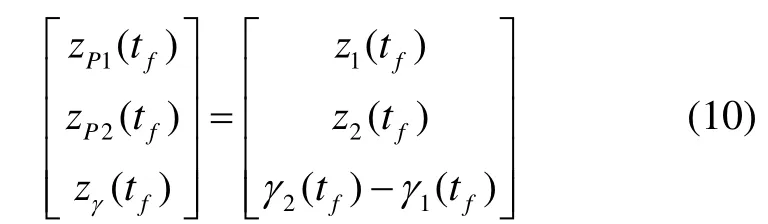
则可以将性能指标式(6)转化为以下形式:

对式(7)两边关于时间t微分,经进一步整理可以得到:

2.2 微分对策制导律推导
基于降阶后的系统(12)和性能指标(11)进行拦截角度协同微分对策制导律的推导。构造哈密顿函数如式(13)所示:

式(13)中: λ1、 λ2和 λγ为待定的拉格朗日乘子。
进一步结合协态方程和横截条件可以求得:

则基于上述条件可以得到导弹1、导弹2和目标的最优制导或规避策略为

式(15)~(17)是关于末端时刻状态的表达形式,需要进一步转化为当前时刻状态才能够用于执行。将式(15)~(17)代入式(10),可以得到三个耦合的微分方程,进行积分求解,则末端时刻状态可表示为

式中:

满足:

式(22)~(24)中函数φ和φ如式(8)和式(9)所示。
将式(18)~(20)带入式(15)~(17),则导弹1、导弹2和目标的最优制导策略可表示为

式(25)~(27)为导弹1和导弹2零控脱靶量和零控协同拦截角误差的线性组合,其中分别为相应的制导增益,且满足:


2.3 制导增益分析

当β→0时,导弹1和导弹2不再存在拦截角度协同上的约束,仅实现脱靶量上的协同,此时对策三方的制导增益为

该无拦截角度协同的双方微分对策制导律在结构上是与文献[2]相类似的,只是在对策关系上,导弹1是与导弹2协同于目标拦截,而不是与载机协同,以保护载机的安全。
当β,η,a2→0时,则转化为导弹1与目标两者之间典型的线性二次型微分对策问题,此时的制导增益为

2.4 对策空间分析
对于零和微分对策问题,不存在共轭点的充分条件是具有鞍点解,而鞍点解当且仅当系统(10)所对应的Riccati微分方程(36)的解是有限时存在[17]。


式(37)经进一步整理可以得到:

式(38)中:

图2给出了不同η值下,ηE随剩余飞行时间tgo的分布曲线,假设导弹1与导弹2速度和控制系统时间常数相同,剩余飞行时间近似相等。从图2中可以看出:ηE>0,满足微分对策线性二次型性能指标中目标控制指令加权参数正定的条件;同时,当tgo足够大时,ηE趋于常值,且该常值大于η。在导弹1控制量一定的条件下,导弹2为实现与导弹1之间的协同,在tgo较大时,所需的控制量大于目标,而在末制导尾端,所要求的控制量则低于目标,因此协同情况下对击中目标更为有利。

图2 不同η下的Eη分布曲线Fig.2 Distribution of Eη with differentη
3 仿真结果及分析
双导弹拦截角度协同制导律的推导基于末制导线性化假设,为充分验证制导律的性能,针对非线性平面相对运动关系进行了仿真和分析。仿真中模拟两枚导弹由同一武器系统同时发射,即初始位置相同,对于两枚导弹初始位于不同空间位置的情况,所推导的协同制导律同样适用。仿真中取导弹飞行速度VP1= VP2=500m/s ,目标飞行速度VE=300m/s ,控制系统时间常数τP1=τP2=0.2s,τE=0.3s ,α1=α2=105,β=108,η=1,ηE=10,两枚导弹的协同拦截角度σ=45°。假设目标机动为“bang-bang”类型,且仅具有一次随机时间切换[13-16],最大机动能力为5g,所得仿真结果如图3~10所示。
图3和图4为初始位置相同的两枚导弹在协同情况下和非协同情况下拦截非机动目标的飞行弹道。在非协同情况下,导弹采用的制导增益和零控脱靶量分别如式(34)和式(7)所示。图3中由于导弹1剩余飞行时间大于导弹2,在拦截角度上更多的协同导弹1,弹道更加弯曲,所需的加速度也相对较大。图5给出了协同情况下两枚导弹的加速度曲线。图6为两枚导弹的协同拦截角度,在达到设定值45°后,导弹加速度也随之减少。
图7和图8为两枚导弹协同拦截机动目标的飞行弹道。协同拦截角度的设计有利于两枚导弹构成特定的拦截态势,如钳形,对于机动目标的拦截有利,也增强了末制导尾端对目标的可观测性。由于两枚导弹之间存在协同拦截关系,所需的加速度较低,最大值与拦截非机动目标的情况相当,且在构成设定的协同拦截态势后,需用加速度逐步减少到目标最大机动能力的2倍以内,如图9所示。图10给出了拦截机动目标情况下的协同拦截角度,满足了设计要求。

图3 飞行弹道,非机动目标,弹间协同Fig.3 Flight trajectory, non-maneuvering target, and cooperation between missiles

图4 飞行弹道,非机动目标,弹间无协同Fig.4 Flight trajectory, non-maneuvering target, and non-cooperation between missiles

图5 导弹加速度,非机动目标,弹间协同Fig.5 Missile acceleration, non-maneuvering target, and cooperation between missiles

图6 两枚导弹的协同拦截角度,非机动目标,弹间协同Fig.6 Cooperative attacking angle between two missiles, non-maneuvering target, and cooperation between missiles

图7 飞行弹道,机动目标,弹间协同Fig.7 Flight trajectory, maneuvering target, and cooperation between missiles

图8 飞行弹道,机动目标,弹间无协同Fig.8 Flight trajectory, maneuvering target, and non-cooperation between missiles
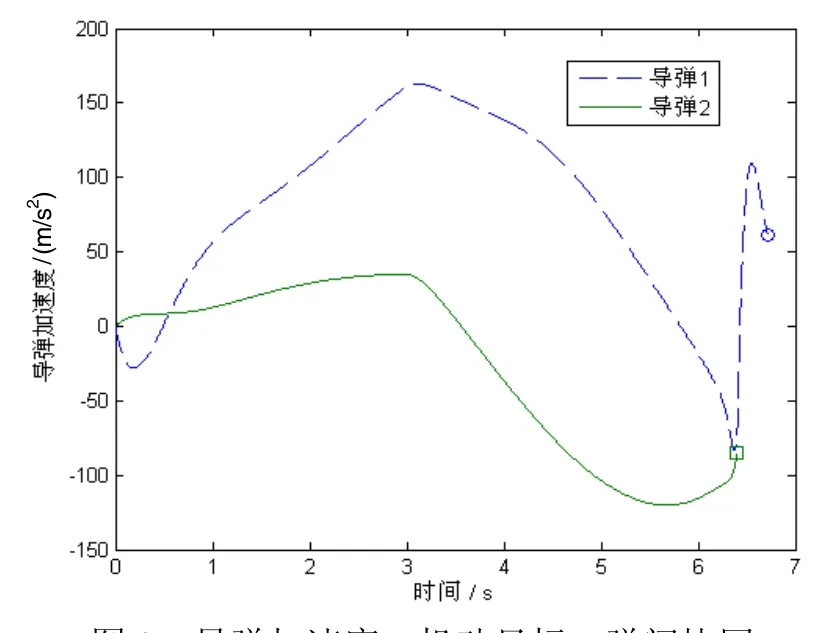
图9 导弹加速度,机动目标,弹间协同Fig.9 Missile acceleration, maneuvering target, and cooperation between missiles

图10 两枚导弹的协同拦截角度,机动目标,弹间协同Fig.10 Cooperated attacking angle between two missiles, maneuvering target, and cooperative missiles
4 结 论
针对两枚导弹协同拦截单个目标的拦截情形进行了微分对策制导律的设计,单枚导弹在减少脱靶量的同时,与另一枚导弹在拦截态势上构成角度上的协同关系。非线性仿真结果表明,由于可构成特定的拦截态势,所推导的微分对策制导律更加有利于机动目标的拦截,且由于导弹之间存在协同关系,对加速度的需求较低,而拦截角度协同也增强了末制导尾端对目标的可观测性。本文基于线性二次型微分对策理论进行三方微分对策制导律的推导,设计方法同样适用于更多枚导弹协同拦截单个目标的情况。
(Reference):
[1] Shaferman V, Shima T. Cooperative multiple-model adaptive guidance for an aircraft defending missile[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(6): 1801-1813.
[2] 花文华, 陈兴林. 主动防御的协同微分对策制导[J].高技术通讯, 2012, 22(1): 94-99. Hua Wen-hua, Chen Xing-lin. Cooperative differential game guidance strategy for active defense[J]. Chinese High Technology Letters, 2012, 22(1): 94-99.
[3] Rubinsky S, Gutman S. Three body guaranteed pursuit and evasion[C]//AIAA Guidance, Navigation, and Control Conference. Minneapolis, Minnesota, 2012: 1-24.
[4] 李新三, 汪立新, 范小虎, 等. 带有末端角度和轨迹路径点约束的MPSC制导律设计[J]. 中国惯性技术学报, 2016, 24(1): 119-124. Li Xin-san, Wang Li-xin, Fan Xiao-hu, et al. Guidance law of model predictive spread control with waypoints and terminal impact angle constraints[J]. Journal of Chinese Inertial Technology, 2016, 24(1): 119-124.
[5] Ryoo C K, Cho H, Tahk M J. Time-to-go weighted optimal guidance with impact angle constraints[J]. IEEE Transactions on Control System Technology, 2006, 14(3): 483-492.
[6] Shima T. Intercept-angle guidance[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 484-492.
[7] Taub I, Shima T. Intercept angle missile guidance under time-varying acceleration bounds[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 686-699.
[8] 花文华, 孟庆龄, 张金鹏, 等. 有界控制导弹攻击防御性飞机的制导律[J]. 中国惯性技术学报, 2016, 24(1): 103-107. HUA Wen-hua, MENG Qing-ling, ZHANG Jin-peng, et al. Guidance law of bounded-control missile for attacking an aircraft with defending missile[J]. Journal of Chinese Inertial Technology, 2016, 24(1): 103-107.
[9] Jeon I S, Lee J I, Tahk M J. Homing guidance law for cooperative attack of multiple missiles[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 275-280.
[10] Foley M H, Schmitendorf W E. A class of differential games with two pursuers versus one evader[J]. IEEE Transactions on Automatic Control, 1974, 19(3): 239-243.
[11] Shinar J, Shima T, Kebke A. On the validity of linearized analysis in the interception of reentry vehicles[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference, Reston, VA, USA, 1998: 1050-1060.
[12] Shima T, Golan O M. Linear quadratic differential games guidance law for dual controlled missiles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 834-842.
[13] 花文华, 孟庆龄, 张拥军. 寻的导弹范数型微分对策制导律[J]. 高技术通讯, 2013, 23(4): 392-399. Hua W H, Meng Q L, Zhang Y J. Norm differential game guidance law for homing missiles[J]. Chinese High Technology Letters, 2013, 23(4): 392-399 .
[14] 花文华, 陈兴林. 变速导弹有界控制非线性微分对策制导律[J]. 控制与决策, 2011, 26(2): 1886-1890. Hua W H, Chen X L. Nonlinear bounded-control differrential game guidance law for variable-speed missiles[J]. Control and Decision, 2011, 26(2): 1886-1890.
[15] Weiss M, Shima T. Minimum effort pursuit/evasion guidance with specified miss distance[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(5): 1069-1079.
[16] Bardhan R, Ghose D. Nonlinear differential games-based impact-angle-constrained guidance law[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(3): 384-402.
[17] Ryoo C K, Cho H, Tahk M J. Time-to-go weighted optimal guidance with impact angle constraints[J]. IEEE Transactions on Control System Technology, 2006, 14(3): 483-492.
Differential game guidance law for double missiles with cooperative intercept angle
HUA Wen-hua1, ZHANG Yong-jun1, ZHANG Jin-peng1,2, MENG Qing-ling1
(1. China Airborne Missile Academy, Luoyang 471009, China; 2. Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons, Luoyang 471009, China)
To improve the kill probability of high-value targets, the guidance law for intercepting a single target by double missiles is studied based on the linear quadratic differential game theory. Each missile attempts to minimize its expected miss distance while also imposes a cooperation attacking angle relative to the other missiles to construct a specific attacking scenario for improving the agile maneuvering target interception and target observability in the end-game phase. The derived differential game guidance law takes into account of the control system dynamics of the game’s three-sides and has closed-form analytic solutions. The solutions are linear combination of zero-effort miss distance and zero-effort cooperative intercept angle error. The guidance gains and differential game space are also analyzed, and the existence condition of the saddle point solution is given. Nonlinear simulations are carried out, and the simulation results show that the acceleration requirements of the missiles are low thanks to the cooperation between the double missiles, and the required accelerations can be further reduced after the designed cooperation attacking angles are converged.
terminal guidance; differential game; cooperation guidance; target interception
V448.133
:A
2016-07-27;
:2016-11-18
航空科学基金项目(2015ZC12006)
花文华(1983—),男,高级工程师,博士,主要研究方向为飞行器制导与控制。E-mail: huawh6611@163.com
1005-6734(2016)06-0838-07
10.13695/j.cnki.12-1222/o3.2016.06.025
