基于Harris特征点和伪Zernike矩的鲁棒水印算法

陈　青,翁旭峰

(上海理工大学 光电信息与计算机工程学院,上海　200093)



基于Harris特征点和伪Zernike矩的鲁棒水印算法

陈青,翁旭峰

(上海理工大学 光电信息与计算机工程学院,上海200093)

摘要抵抗几何攻击的鲁棒性是目前数字水印技术中的热点亦是难点。文中以Harris检测算子和伪Zernike矩为理论基础,提出一种有效抵抗几何攻击的鲁棒水印算法。通过提取归一化图像的Harris特征点,选取部分稳定特征点确定圆形区域并计算伪Zernike矩,并量化调制伪Zernike矩的幅值来嵌入水印信息。实验结果表明,本算法对于抗几何攻击具有较好的鲁棒性,同时也能抵抗常规的信号处理攻击。

关键词特征点;Harris检测算子;伪Zernike矩;几何攻击;信号处理攻击

A Robust Image Watermarking Based on Harris Feature Points and Pseudo-Zernike Moments

CHEN Qing,WENG Xufeng

(School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

AbstractThe improvement of the robustness watermarking against geometrical attacks is still a difficult and open problem for watermarking researchers.This paper proposes a geometrically invariant watermarking algorithm based on Harris detector and the pseudo Zernike moment.First the Harris detector is utilized to extract steady feature points from the standard image,then the local feature regions are ascertained according to the feature scale theory,and finally the digital watermark is embedded into the local feature regions by quantizing the magnitudes of the pseudo Zernike moments.Experimental results show that the proposed watermarking algorithm is robust to geometric attacks as well as to common signal processing attacks.

Keywordsfeature points;Harris detector;pseudo Zernike moments;geometric attacks;signal processing attacks

数字水印技术作为信息隐藏的重要分支是目前版权保护的有效手段。近年来对于图像数字水印的鲁棒性研究已取得较大进展,但面临旋转、缩放、平移等几何攻击(RST攻击)仍存在较大困难。几何攻击破坏了水印提取与嵌入的同步性,微小的几何攻击就能使得水印检测失败[1-2]。因此,设计能够抵抗几何攻击的水印算法成为水印研究的一个新的热点。

传统的数字水印算法一般是在空间域或频域嵌入水印,其缺点是水印信息并不是嵌入到数据最重要的部分。为此,Kutter等人[3]提出所谓第二代数字水印概念,其基本思想是充分利用图像的内在特征进行水印嵌入。在众多图像特征中,特征点一般具有几何不变性,因此以特征点为参考来嵌入水印可抵抗几何攻击。Bas等人[4]给出一种基于图像特征点的数字图像水印算法,该算法首先利用Harris算子提取特征点,然后对特征点集进行Delaunay Tessellation三角剖分,得到互相连接的三角形区域,最后将水印信号嵌入到每个三角形区域中,而水印检测是通过利用不同三角区域的相关性来完成的。Tang等人[5]提出另一种比较经典的基于图像特征点的抗几何攻击水印算法,该算法利用墨西哥帽小波的尺度交互特性提取特征点并生成圆形区域,然后在离散傅里叶变换域嵌入水印,由于是在DFT域中嵌入的,相比Bas等人的算法,该算法的鲁棒性得到较大提高。

通过对已有算法以及Harris算子的研究,本文提出一种基于Harris特征点与伪Zernike矩结合的抗几何攻击水印算法。与Zernike矩相比,伪Zernike矩同样具有几何不变性,且具有更加丰富的低阶矩和更好的抗噪声能力[6-7]。本算法首先利用Harris算子提取出归一化图像的特征点,对于部分最稳定的特征点取其半径为R的圆形区域计算伪Zernike矩,通过量化调制伪Zernike矩的幅值来嵌入水印信息。实验结果表明,该算法对于几何攻击与常规的信号处理攻击均具有良好的鲁棒性。

1基本理论

1.1Harris算子

Harris算子是一种基于静止图像的特征点提取算子,其利用自相关函数来确定图像信号发生二位变化的位置。Harris算子检测步骤如下

(1)

RH=det(M)-k×Trace2(M)

(2)

式(1)中,gx和gy分别是x轴方向和y轴方向的梯度;G(s)是高斯平滑函数,式(2)中,det是矩阵的行列式,Trace是矩阵的迹,k为常数,一般取0.04~0.06。将响应值RH与阈值T比较即可检测出特征点的位置。且阈值设置越大,检测出的特征点数量越少。此外,响应值越大表明特征点的鲁棒性越好。

图1为标准图像Lena和Peppers进行Harris特征点检测的结果。从图中可以看出,Harris特征点主要集中在图像纹理复杂的区域和有明显灰度变化的地方[8]。

图1　Harris特征点检测的结果

并不是所有的特征点都适用于嵌入水印,本算法选取响应RH较大的特征点,取其半径为R的圆形区域来嵌入水印信息。该圆形区域中可能含有其他特征点,以免水印信息互相影响,需要进一步筛选出部分特征点以获得互相不重叠的圆形区域。这一优化操作可通过以下步骤完成:

(1)对于所有检测出的Harris特征点记作集合Ω1,从Ω1选出响应值最大的特征点,记作P0;

(2)判断P0以外的每一个特征点及其圆形区域,若与P0对应的圆形区域存在重叠则从Ω1中去除那些特征点,并保留P0到集合Ω2中;

(3)将P0从集合Ω1去除;

(4)若Ω1中剩余特征点对应的圆形区域仍存在相互重叠的情况,则重复步骤(1)至步骤(3),否则转入步骤(5);

(5)用集合Ω2生成互不重叠的圆形区域。

1.2伪Zernike矩

图像的伪Zernike矩[6]是将图像映射到一组基函数上得到的,称为伪Zernike矩的基。这组基构成了单位圆(x2+y2≤1)内一组完备的正交集,其定义为

Vnm(x,y)=Vnm(ρ,θ)=Rnm(ρ)exp(jmθ)

(3)

(4)

对于一幅大小为N×N的数字图像,伪Zernike矩定义为

(5)

其中,xi+yi≤1,并且Δx=Δy=2/N。

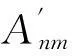
(6)

2水印算法描述

2.1水印的嵌入

将数字水印系统看成一个通信模型,即将载体看作信道,数字水印看作被传输的信息,各种有意或无意的攻击看作噪声干扰,载体图像中每个特征点生成的圆形区域可看成是独立的传输信道。若将水印信息重复嵌入每个区域中,即使有一部分信道遭到损坏,其余信道仍可保证水印信息的正常传输。水印的嵌入过程具体有如下步骤:

(1)由密钥Key生成长度为L的伪随机二值序列W1={wi,i=1,2,3,…,L}作为水印信息,本文中L取32;

(3)以集合Ω2中的特征点为圆心,R为半径,计算每个圆形区域的伪Zernike矩,根据相关理论[10],部分伪Zernike矩的计算值是不准确的,这些矩不能嵌入水印。选择时一般考虑以下两方面:1)矩的最大阶数Nmax不能大于一个特定的阶数,本文选取Nmax=18;2)重复度m=4i(i=1,2,3…)的矩计算是不准确的,因此不能用于嵌入水印。最终选取的矩集合可表示为A={Anm,n≤Nmax,m≥0,m≠4i};

2.2水印的检测

水印检测过程是水印嵌入的逆过程,在本算法中,水印检测属于盲检测,即检测时无法借助原始信息。由于水印信息被重复嵌入到每个圆形区域中,且每个区域彼此独立。因此可用相同的方法提取水印,只要两个以上的区域能够检测到水印,便可认为水印存在于图像中。检测过程具体有以下几个步骤:

(1)对含有水印的图像进行尺度归一化,消除图像缩放带来的影响;

(2)进行Harris特征点提取。若含有水印的图像受到信号处理攻击或几何攻击,应仍有部分特征点保留下来;

(4)逐个提取后得到长度为L的二值序列W2,再次借助密钥Key生成原始水印信号W1,计算W2与W1的归一化相关系数NC(NormalizedCorrelation)来衡量水印的相似性。W2与W1的NC定义为

由NC可判断图像中是否嵌入水印,水印是否存在可用最大相似性检测器(MLD)来判断

if NC≥h⟹H1,if NC

H1表示图像含有水印,H0表示图像中没有水印。h是决策阈值,其的选择同时兼顾虚警率和漏警率,本算法中选取一个折衷值h=0.6,此时能较好地反映水印检测的准确性。

3实验结果

实验使用Matlab 7.0作为验证平台,分别给出检测性能测试、抗攻击(包括常规信号处理和几何攻击)测试的实验结果。试验中,所采用的原始载体分别为256×256的灰度图像Lena,Peppers和Baboon,采用长度为32位的伪随机二值序列作为水印信息。量化步长选取q=1.5时水印的可见性与鲁棒性取得平衡,峰值信噪比PSNR分别为43 dB (Lena),41 dB (Peppers)和40 dB (Baboon),此时肉眼很难看出水印存在。对于原始载体Lena,Peppers和Baboon,用本文方法确定的局部区域数目分别为6,7和8。图2给出原始图像以及未受到攻击时对含水印图像的检测结果,分别能正确提取出6,6,7个含有水印信息的圆形区域。

图2　含水印图像的检测结果

3.1几何攻击

对于本算法,缩放和旋转这类常见的几何攻击是需要尤其关注的。表1给出了实验结果,数字表示从攻击后含水印图像中成功检测到数字水印的局部特征区域数目,只要两个以上区域能检测到水印,便可认为水印存在于图像中。

表1　数字水印抗几何攻击能力

3.2信号处理攻击

信号处理攻击包括有损压缩、添加噪声、图像滤波等。对各类型攻击选择不同参数进行实验。结果表明本算法对于信号处理攻击同样具有较好的鲁棒性,说明伪Zernike矩本身具有对噪声不敏感的优良特性。实验结果如表2所示。

表2　数字水印抗常规信号处理攻击能力

4结束语

本文以Harris算子和伪Zernike矩为理论基础,提出一种有效抵抗几何攻击的第二代数字水印算法。其特点如下:(1)对原始图像进行归一化处理,消除了缩放的影响;(2)所提取的的图像特征点稳定性好,且分布较均匀,适合抵抗图像受到的随机剪切;(3)结合伪Zernike矩的优点,使本算法具有旋转不变性,并具有较好抵抗JPEG压缩和噪声等常规攻击的能力。

参考文献

[1]Lee C H,Lee H K,Suh Y.Image watermarking resistant to combined geometric and removal attacks[J].International Journal of Image and Graphics,2006,5(1):37-66.

[2]Liu Jiufen,Huang Daren,Huang Jiwu.Survey on watermarking against geometric attack[J].Journal of Electronics and Information Technology,2004,26(9):495-1503.

[3]Kutter M,Bhattacharjee S K,Ebrahimi T.Towards second generation watermarking schemes[C].Proceedings of International Conference on Image Processing,1999(1):320-323.

[4]Bas P,Chassery J M,Macq B.Geometrically invariant watermarking using feature points[J].IEEE Transactions on Image Processing,2003,11(9):1014-1028.

[5]Tang C P,Hang H M.A feature based robust digital image watermarking scheme[J].IEEE Transactions on Signal Processing,2003,51(4)950-958.

[6]叶斌,彭嘉雄.伪Zernike矩不变性分析及其改进研究[J].中国图象图形学报,2003,8(3):246-252.

[7]Tsougenis E D,Papakostas G A,Koulouriotis D E,et al.Performance evaluation of moment based watermarking methods:a review[J].Journal of Systems and Software,2012,85(8):1864-1884.

[8]Wang Xiangyang,Yang Yiping,Yang Hongying.Invariant image watermarking using multi-scale Harris detector and wavelet moments[J].Computers and Electrical Engineering,2010,36(1):31-44.

[9]Kim H S,Lee H K.Invariant image watermark using zernike moments[J].IEEE Transactions on Circuits and Systems for Video Technology,2003,13(8):766-775.

[10]Liao Simon,Miroslaw Pawlak.On the accuracy of Zernike moments for image analysis[J].IEEE Transactions on Pattern Anal Machine Intell,1998,20(12):1358-1364.

中图分类号TN492

文献标识码A

文章编号1007-7820(2016)03-183-04

doi:10.16180/j.cnki.issn1007-7820.2016.03.048

作者简介:陈青(1962—),女,博士,副教授,硕士生导师。研究方向:信号处理。翁旭峰(1988—),男,硕士研究生。研究方向:数字水印。

基金项目:上海自然科学基金资助项目(12ZR1420800);国家863计划基金资助项目(2012AA050206)

收稿日期:2015- 07- 08