基于奖励因子的囚徒困境博弈模型研究
2016-04-14陈维春尚丽辉
陈维春,尚丽辉
(上海理工大学 光电信息与计算机工程学院,上海 200093)
基于奖励因子的囚徒困境博弈模型研究
陈维春,尚丽辉
(上海理工大学 光电信息与计算机工程学院,上海200093)
摘要针对合作演化问题,通过引入奖励因子。根据演化博弈论,研究在空间囚徒困境博弈中,奖励因子和记忆长度对策略改变的影响。先后分析了合作率与对背叛诱惑之间的关系图,合作率与记忆长度的关系图以及临界值和奖励因子变化的关系图等。研究发现,与传统囚徒困境博弈模型相比,增加奖励因子或减少记忆长度能有效促进合作的演化。
关键词囚徒困境博弈;奖励因子;收益系数
Research on Prisoner’s Dilemma Game Based on Reward Factor
CHEN Weichun,SHANG Lihui
(School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
AbstractThe evolution of cooperation is discussed according to the evolutionary game theory.We study the reward factor and memory during the strategy update process by introducing the reward factor in the spatial Prisoner’s Dilemma Game.Firstly,we analyze the rate of cooperation and the temptation of betrayal,the relationship cooperative rate and memory length,and the relationship diagram of critical value and reward factor.A comparison with traditional Prisoner’s Dilemma Game Model shows that increasing the reward factor or reducing the memory length effectively promotes the evolution of cooperation.
Keywordsprisoner’s dilemma game;reward factor;coefficient
在自然界和人类社会中广泛存在着合作行为[1-9]。在传统的囚徒困境博弈模型中[10],每个参与者均有两种策略选择:合作或者背叛。若两个参与者均选择合作,则每个人可得到较高收益,记为R;若两个参与者均选择背叛,则每个人会得到较低的收益,记为P;而如果一个参与者选择合作而另一个选择背叛,则合作者会得到最低的傻瓜式报酬,记为S,而背叛者可得到最高的收益,即对背叛的诱惑,记为T。因此,可得到T>R>P>S。可以看出,自私的个体会选择背叛,而不会考虑对手的选择。因而,这种困境行为会导致背叛者大量出现。
本文通过引入奖励因子的概念,研究空间囚徒困境博弈中,奖励因子和记忆长度对策略改变的影响。若参与者能将自身的策略连续M代或M代以上逐代传给其的后代而不间断,就给予适当的奖励。在博弈进行之前,为每个参与博弈的个体设置相同的收益系数,记为φx(t),其会使博弈返回到传统的博弈模型,在演化的过程中,随着策略和记忆长度的改变,每个参与者的收益系数也会随之发生变化。
1模型
不妨假设参与者位于L×L周期性边界条件x点的平方格子上,初始时,参与者在点x处作为合作者(ss=C)或背叛者(sx=D)的概率是相等的,收益系数φx(t)=1.0也相等。为研究方便,调整收益矩阵[11-13]:对背叛的诱惑T=b,相互合作时的收益R=1,相互背叛时的收益P和傻瓜式的报酬S都等于0,在此取1≤b≤2。根据Monte Carlo(MC)仿真,首先,参与者通过与其最近的4个邻居进行博弈,获得本轮收益Px,然后通过表达式(1)计算其的总收益φx
φx=φx(t)·Px
(1)
其次,随机选择一个邻居,记为y,以同样的方法计算φy。最后,下一轮中参与者x采取y的概率可根据物理学中的费米函数计算
(2)
这里K描述了环境的噪声因素。在本模型中,若参与者能将自身的策略逐代地传给其的后代连续进行M或M代以上,而中间不改变其策略,就给予适当的奖励,且在x的收益系数φx(t)将会以表达式(3)发生变化,即
φx(t+1)=(1+α)·φx(t)
(3)
这里α(0≤α≤1)即为奖励因子,否则收益系数φx(t)保持不变。若参与者在连续M代以内的某一子代改变了其策略,即采用其邻居的策略,就不再给其奖励,并将那一代看作是第一代重新计算,这一过程反复进行,直至收益系数重新返回到1.0为止。
2仿真结果及分析
文中考虑节点在50×50的网格上,设定MCS为1.1×104,为保证结果的准确度,每个仿真结果均为进行100次仿真并取平均值的结果。
首先,观察在M保持不变的情况下,奖励因子α与合作演化之间的关系。如图1所示,仿真了当M=3,奖励因子分别取α=0,0.01,0.02,0.03,0.04时,合作率ρc与对背叛的诱惑b之间的关系,这里取K=0.1。
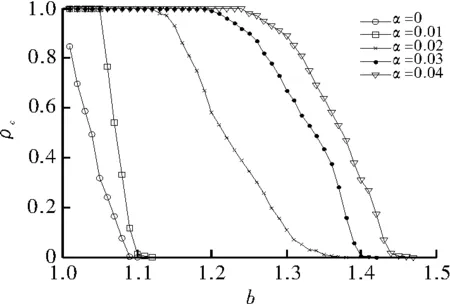
图1 奖励因子α与合作演化之间的关系图
图1所示,当α=0时,此博弈模型回归传统的囚徒困境博弈模型,在b较小时合作者就会消失。然而,随着α的增加,有效地促进了合作的演化。当α=0.01时,可明显看出在b较小时合作被有效地促进,就是合作占优的策略。随着α地持续增加,背叛者只有在b足够大时才会存在。这些结果表明,当引入奖励因子时,合作的出现与维持可被有效促进,增加奖励因子会导致合作的演化。
接着观察记忆长度M对合作演化的影响。在图2中,仿真了当奖励因子取α=0.02,M=1,3,6,9,12时,ρc与b的关系,取K=0.1。

图2 合作率ρc与b的关系图
图2所示,随着M值的减小,合作演化被有效地促进,随着M值的减小,合作者的生存能力会单调增加。以上结果表明,当奖励因子取定适当值时,随着记忆长度M的减小,合作演化可被有效地促进。当奖励因子取α=0.02,b=1.1,1.2,1.3,1.4时,ρc与M的关系如图3所示,取K=0.1。

图3 ρc与M的关系图
如图3所示,在一定范围内,随着b的减小,合作演化被有效地促进,在b=1.1时,可明显看到是合作占优的策略。当M值足够大时,这种促进作用就会越来越微弱甚至消失。这从图2中得到了验证。
最后,考虑临界值bc,就是使合作者消失时刻的值。当M=3,6,9,12时,bc随α变化的关系如图4所示,取K=0.1。
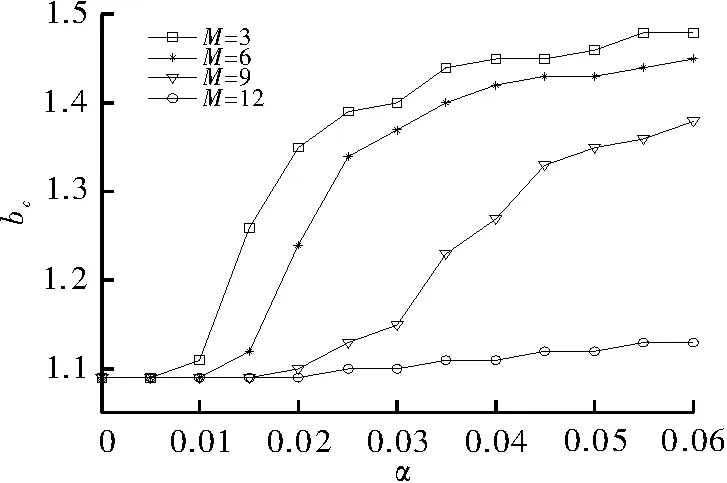
图4 临界值bc随α变化的关系图
图4所示,与传统的囚徒困境博弈模型(α=0)相比,随着α的增大,bc单调增加,对不同的M值而言,合作者生存能力的健壮性是不同的,其定性的分析结果从图1中可得到验证。引入奖励因子,可促进合作的演化;另一方面,随着M值的减小,合作者的生存空间变的越来越广泛,图2中的结果也证实了这一结论。
3结束语
本文研究了在空间囚徒困境博弈中,奖励因子和记忆长度对策略改变的影响。研究发现,这种奖励机制能有效地促进合作。随着奖励因子的单调增加或记忆长度的减少,合作行为可明显得到促进,通过合作的动态演化,也证实了该种奖励机制能有效促进合作。
参考文献
[1]Dugatkin L A.Cooperation among animals:an evolutionary perspective[M].Princetion,NJ:Oxford University Press,1997.
[2]Maynard Smith J,Szathmáry E.The major transitions in evolution[M].Princetion,NJ:Oxford University Press,1995.
[3]Axelrod R.The evolution of cooperation[M].New York:Basic Books,1984.
[4]Sigmund K.The calculus of selfishness[M].Princeton,NJ:Princeton University Press,2010.
[5]Nowak M A.Evolutionary dynamics:exploring the equations of life[M].Cambridge,MA:Belknap Press,2006.
[6]Hofbauer J,Sigmund K.Evolutionary games and population dynamics[M].Cambridge,UK:Cambridge University Press,1998.
[7]Colman A M.Game theory and its applications in the social and biological sciences[M].Oxford,UK:Butterworth-Heinemann,1995.
[8]Taylor M.The possibility of cooperation[M].Cambridge,UK:Cambridge University Press,1987.
[9]杨涵新,汪秉宏.复杂网络上的演化博弈研究[J].上海理工大学学报,2012,34(2):166-171.
[10]汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版,2012.
[11]Tomochi M,Kono M.Spatial prisoner’s dilemma games with dynamic payoff matrices[J].Physical Review E,2002(65):026112-026119.
[12]Ashlock D,Kim E Y,Ashlock W.A fingerprint comparison of different prisoner’s dilemma payoff matrices[J].IEEE Transportations on Biological Science,2010(6):219-226.
[13]Li Z H,Wang B H,Liu R R,et al.Evolutionary prisoner’s dilemma game based on division of work[J].Chinese Physical Letters,2009,26(2):108701-108710.
中图分类号F224.32
文献标识码A
文章编号1007-7820(2016)03-005-03
doi:10.16180/j.cnki.issn1007-7820.2016.03.002
作者简介:陈维春(1988—),男,硕士研究生。研究方向:复杂网络。尚丽辉(1977—),女,博士,讲师。研究方向:复杂系统的分析与控制。
基金项目:国家自然科学基金资助项目(81101116)
收稿日期:2015- 07- 28
