基于反电势线性拟合的无霍尔BLDC驱动方法

丁　亮,丁学明

(上海理工大学 光电信息与计算机工程学院,上海　200093)



基于反电势线性拟合的无霍尔BLDC驱动方法

丁亮,丁学明

(上海理工大学 光电信息与计算机工程学院,上海200093)

摘要对于以反电势过零点判断来控制无感直流无刷电机的方案,在驱动的低速阶段,由于反电动势值过小,难以准确地检测过零点,针对该问题,提出一种新的低速反电势过零检测方法。该方法在低速采用线性拟合代替硬件判断反电势过零点,并在PWM_OFF时刻进行反电势采样,提高了低速阶段的控制性能,通过Matlab的Simulink仿真证明该方案切实可行。

关键词无感BLDC;反电势过零检测;采样点;线性拟合

A Method of Driving Without Hall BLDC Based on Linear Fit BEMF

DING Liang,DING Xueming

(School of Optical-Electronic Information and Computer Engineering,University of Shanghai for Science and Technology,Shang 200093,China)

AbstractAs for the scheme based on back EMF zero crossing detecting to drive the sensorless brushless dc motor,it is difficult to accurately detect zero crossing points in the drive of low speed stage because the back EMF value is too small.This paper puts forward a new method of the back EMF zero crossing detection at low speed.This method drives by linear fitting instead of hardware to determine the zero crossing at low speed,and the back EMF is sampled in pwm_off time,thus improving the control performance of low speed stage.Matlab simulink simulation proves that the scheme is feasible.

Keywordssensorless BLDC;back emf zero crossing point detection;sampling point;linear fitting

传统直流电机因控制简单一度是运动控制和伺服控制的主流,但随着科技的发展和改进,人们对电机的控制有着越来越多的苛刻的要求。传统直流电机也越来越无法满足日益复杂的驱动环境:其物理电刷和换向器严重影响了电机的使用寿命,使得其故障率高,不易维护。为避其短板,无刷直流电机(BLDC)应运而生,BLDC没有物理换向器和电刷,使其寿命大幅增加,有统计显示传统直流电机的使用寿命大概约在6 000 h,而直流无刷电机的使用寿命约在15 000 h,增加了近2倍[1]。

BLDC的特点是:运行效率高、运行平稳、结构集成、可靠、维护少。当然,硬件上替换掉了换向器和电刷,在驱动上就要比传统直流马达复杂,其中难点便是换相点的确定。传统直流电机依靠电刷和换向器可以准确换相,而BLDC就必须依靠其他的方法来确定转子的位置,经典方法有基于硬件定位和基于软件定位,前者是有感BLDC控制,后者便是无感BLDC控制。

有感BLDC控制中较为常见的是基于霍尔元件和编码器的确定转子位置的方法,即通过霍尔传感器或编码器的不同状态,来决定线圈的通电顺序和方向,使得定子磁场始终领先于转子磁场[2]。该方案已得到普遍应用,但仍存在诸多问题:集成霍尔传感器或者编码器不但会增加马达的成本,还会使马达结构变复杂,结构复杂带来的后果便是马达故障率较高[3]。且霍尔传感器对于温度较为敏感,要运行在75 ℃以下,且磁敏,这就限制了霍尔BLDC的使用环境,还可能降低马达的可靠性[4]。甚至在某些环境下,鉴于BLDC容积的限制,安装位置传感器是不被允许的[5]。有鉴于此,无感的BLDC控制方案开始出现并逐渐流行。

目前主要的无霍尔控制方案是基于反电势检测信息判断换相点,本文研究反电势在PWM-OFF点的检测方案确定换相点。

1PWM-OFF反电势检测方案

对BLDC的模型做等效,将线圈阻抗看成是一个线性电阻和一个储能电感的等效,其等效电路图如图1所示。

图1　BLDCM等效电路图

电机三相绕组输出端电压的电压方程组为

(1)

(2)

(3)

式中,LM=L-M;Ua0、Ub0和Uc0为三相绕组输出端对直流电源地的电压。ea、eb、ec为A、B、C三相绕组的反电动势;ia、ib、ic为A、B、C三相绕组的相电流;uN为三相绕组中性点N对电源地的电压,r为每相绕组的电阻。

反电势过零检测判断换相点的原理如图2所示。

图2　反电势波形与过零点检测波形

在检测到过零点之后做一个信号翻转,可见过零点和换相点之间有一个30°的相位差,即在文中检测到反电势过零点事件后,再延迟30°电角度的时间便启动换相,这样就实现了电机的驱动[6]。

在PWM-OFF时刻采样端电压,其电路原理如图3所示。

现依然假设A、B两相导通,C相关断,对于C相,易得

Vc=ec+vn

(4)

对于A相,忽略二极管正向管压降,可得

(5)

对于B相,忽略开关压降,可得

(6)

有A、B两相电压方程可得

vn=-(ea+eb)/2

(7)

对于一个平衡的三相系统可知

ea+eb+ec=0

(8)

于是可得中性点的电压方程为

vn=ec/2

(9)

继而推得C相端电压方程为

(10)

可看出此时端电压和反电势在数值上存在线性对应关系,此时可用端电压的过零点来代替反电势的过零点,又因此时C相的端电压采样是在PWM-OFF时刻进行的,所以没有高频开关噪声影响,精确率高。在端电压检测电路上还要做一些改进,可大幅提高该方案的实用性[7]。

2线性拟合

理论上讲反电势信号的上升沿和下降沿均是线性或接近于线性的直线,如图4所示。

图4　反电势与相电流

对于无感BLDC来讲,其启动过程较为困难,因为可供检测的反电势信号过小,过零点不易判断,所以要在反电势的上升沿和下降沿对反电势信息进行线性拟合,对过零点事件进行预判,这样就能提高换相的精度,利于电机启动和运行,在反电势检测中对数据进行滚动更新,能做到较好的实时性[8]。

线性拟合算法用经典的最小二乘法,假设拟合后的直线方程为

y=f(x)=a+bx

(11)

则依据使拟合结果误差平方和最小,即所测yi与估计值f(xi)=a+bxi之间误差的平方和最小,即

s=∑[yi-f(xi)]2=∑[yi-(a+bxi)]2→min

(12)

此时拟合的公式即为最佳经验公式。解得

(13)

(14)

对应过零点的坐标为

(15)

可将所得零点视作反电势过零点,再在过零点的基础上进行30°电角度的延迟即可换相。该方法的优点是:在低速阶段,当反电势较小时能得到相对准确的换相点,且能滤除一定的杂波干扰使得电机的加速阶段更加稳定平滑。由于拟合本身需要一定的时间,所以在电机高速运转时,可能会造成换相延迟,故可在电机加速阶段使用拟合,而在电机切换到闭环之后再变为反电势检测换相[9]。原始采样点与线性拟合效果如图5所示。

图5　线性拟合效果图

3模型仿真

Matlab仿真中,BLDCM参数设置为:额定转速n=1 000 rpm;定子相绕组电阻r=1.25 Ω;定子相绕组自感L=0.055 H;互感M=0.004 H;转动惯量为0.006 kg·m2;反电势系数为Ke=0.22 V/rad·s-1。极对数为np=1,72 V直流电源供电。可得到系统转速、相电流和相反电动势仿真响应曲线如图6～图9所示。

图6　转速响应曲线

图7　转矩响应曲线

图8　相电流波形

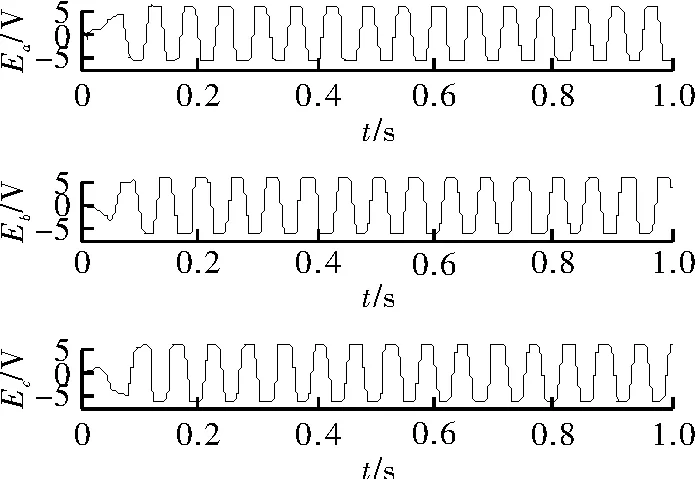
图9　相反电动势波形

由仿真波形可看出,在n=1 000 rpm参考转速下,系统响应快速且平稳,高速阶段相电流和反电势波形较为理想,仿真波形图表明:起动阶段系统保持转矩恒定,因而没有造成较大的转矩和相电流冲击,参考电流的限幅作用有效;空载稳速运行时,忽略系统的摩擦转矩,因而此时的电磁转矩均值接近于零。但在启动阶段相电流有轻微振荡,转矩脉动较大,这是需要改进之处。本文提出的无感直流无刷驱动方案是切实可行的。

参考文献

[1]王季铁,曲家骐.执行电动机[M].北京:电子工业出版社,1997.

[2]邓兵,潘俊民.无刷直流电机控制系统计算机仿真[J].计算机仿真,2002,18(5):104-106,110.

[3]徐昕,李涛,伯晓晨,等.Matlab工具箱应用指南:控制工程篇[M].北京:电子工业出版社,2000.

[4]薛定宇,陈阳泉.基于Matlab/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2002.

[5]纪志成,沈艳霞,姜建国.基于Matlab无刷直流电机系统仿真建模的新方法[J].系统仿真学报,2003,14(12):1745-1749,1758.

[6]Miller T J E.Brushless permanent-magnet and reluctance motor drives[M].Oxford,NewYork:Clarendon Press,1989.

[7]Thomas Salem,Tim A Haskew.Simulation of the brushless DC machine[C].USA:Proceedings of the Twenty-Seventh Southeastern Symposiumon System Theory (SSST’95),1995.

[8]Ionel D M,Eastham J F,Betzer T.Finite element analysis of a novel brushless DC motor with flux barriers[J].IEEE Transactions on Magnetics,1995,31(6):3749-3751.

[9]Jmok H S,Choe G H.A new simulation model of BLDC motor with real back EMF wave form[C].USA:Proceeding from Computers in Power Electronics,The 7th Work shop on Volume Computers in Power Electronics,2000.

中图分类号TM386

文献标识码A

文章编号1007-7820(2016)03-175-04

doi:10.16180/j.cnki.issn1007-7820.2016.03.046

作者简介:丁亮(1990—),男,硕士研究生。研究方向:直流无刷电动机驱动与控制。

收稿日期:2015- 08- 12