一种快速的超像素分割方法

刘　俊

(西安电子科技大学 电子信息攻防对抗与仿真重点实验室,陕西 西安　710071)



一种快速的超像素分割方法

刘俊

(西安电子科技大学 电子信息攻防对抗与仿真重点实验室,陕西 西安710071)

摘要围绕图像分割算法介绍了一种快速的超像素分割算法,传统的分割算法在算法效率,计算成本,复杂度等方面均存在问题。围绕着以上问题,进而提出了一种改进型的算法:超像素分割算法SLIC,并通过实验测试数据性能参数比对,证明了该种算法的优越性,且获得了更好的品质和更高的计算效率。

关键词像素;超像素;图像分割;分割算法

A Fast Method of Superpixel Segmentation

LIU Jun

(Key Lab.of Electronic Information Countermeasure and Simulation,Xidian University,Xi’an 710071,China)

AbstractThis paper introduces a fast method of superpixel segmentation according to image segmentation algorithm in view of the fact that traditional segmentation algorithms have many problems such as the efficiency of the algorithm,computing costs and complexity.An improved algorithm,namely the superpixel segmentation (SLIC),is proposed to address these problems.Experiments and data comparison show that the proposed method offers better quality and higher computational efficiency than other state-of-the art algorithms.

Keywordspixel;superpixels;image segmentation;segmentation algorithm

超像素是利用像素与像素之间特征的相似程度对像素进行分组,从而获取图像的冗余信息,大幅降低了后续图像处理任务的复杂程度。要使超像素能变得实用其必须使用速度快、操作简单。同时,能产生高质量的分割。然而多数最先进的超像素方法均无法满足这些要求。本文所提出的SLIC(简单线性、迭代聚类)算法在由CIELAB色彩空间中的l,a,b值和x,y坐标像素所构成的五维空间中执行一个局部的像素点聚合。一种新的距离度量能实现超像素形状的紧凑、有规则,并能无缝隙地包含灰度及彩色图像。

1SLIC算法

1.1算法原理

SLIC(简单线性迭代聚类)是一种通过利用像素的颜色相似度和图像片面空间对像素进行聚类,从而有效生成紧凑地几乎统一化的超像素分割方法。SLIC分割方法使用简单,给定所需得到的超像素数量即可,且运行速度快,只需线性的运行时间和存储空间。SLIC分割方法生成的超像素具有较好的紧凑性和边界贴合度,超像素大小一致且形状均匀。因此,众多基于像素的图像处理算法采用SLIC超像素来代替像素进行运算,已产生了良好的效果。

本文的方法(SLIC)是在五维空间labxy中来实现的,其中lab为CIELAB色彩空间中的像素颜色矢量,被认为是小颜色距离感知统一,xy是像素点的位置。在CIELAB空间中两种颜色的最大可能距离受到限制,在xy平面上空间距离取决于图像大小。在五维空间中没有规范化空间距离的情况下简单使用欧几里得距离是不可能的。为在五维空间中聚集像素点,本文引进了一种考虑超像素大小的距离测量法。使用该方法,在五维空间中执行颜色相似度和像素点相似度以此便于所期待的群集大小及其空间范围近似相等。

1.2距离测量

本文算法是将一系列要求近似等大超级像素点K作为输入。由于一幅图像有N个像素点,因此每个超级像素点近似大小为N/K个像素。对于大致相等的超级像素点将会有以每个网格间距为超级像素点的中心。

在开始算法前,以固定的网格间距S选择超级像素点K中心和k=[1,K] 。任何一个超级像素点的空间范围近似为S2(一个超级像素点的近似区域),由此可大胆假定在xy平面上围绕一个族群中心的像素点是关联在族群中心2S×2S区域内。这将成为每一个族群中心最近像素点的搜索域。

在CIELAB颜色空间的欧几里德几何距离用于感知有意义的最小距离。若空间像素距离超过能感知的颜色距离,其将开始超出像素颜色相似规律。因此,代替在5D空间的欧几里德几何距离,本文采用一种距离测量Ds,定义为

(1)

其中,k和i分别为两个像素;Ds表示两个像素之间的距离,是像素颜色距离和图像平面中位置距离的加权和。变量m的引入方便控制超像素的紧凑性,变量m的值越大,对紧凑性的要求越高,族群越密集。变量值可以是1～20中的随机数,在本文中选择m=10作为最终结果。该种大致的方法可匹配最大的有意义感知距离经验值,同时能较好的平衡颜色相近和空间相近。

1.3核心算法

LIC算法总结在算法1中。本文定期采样K来开始间隔的族群中心,同时移动其到相应的种子点位置对应于3×3相邻的区域内梯度最小的位置。这是为了避免将其放置到边缘处和减小选择噪声像素点的几率。图像梯度计算公式如下

(2)

在图像中的每个像素点均关联在可以是搜索域重叠的像素点最近的族群中心。在所有像素点被关联在最近的族群中心后,一个新的中心将计算成为属于这一族群所有像素点的平均labxy矢量。然后再反复重复这一过程,以最近的族群中心关联像素点和重新计算族群中心直至收敛。在这一过程结束后,少量迷失的颜色存在,这就是少量像素点在邻近的较大分割段还有同样的颜色,但并未与其关联。同时,其极为稀有,可能会上升,尽管空间邻近测量时聚集并未明确的实现连通。然而在算法的最后阶段实现连通性,通过最大颜色相邻的族群来确认不相交的分割段。算法时间复杂度为O(N),少用至少10%的时间来分割一幅图像。

算法1高效率超像素分割。(1)以S为网格边长,在每个网格中选取一个超像素中心,并在其该像素的3×3邻域内选择梯度最小的像素作为真正的区域中心;(2)对每个区域中心在其2S×2S邻域内搜索属于该区域的像素,将所有像素关联到与其最近的区域中心;(3)在分割出的超像素中计算新的中心像素,并计算剩余误差error;(4)重复步骤(2)和步骤(3),当误差error足够小时,超像素分割结束。

2SLIC算法复杂度分析

在分析SLIC算法复杂度之前,先分析K-means[1-3]算法的复杂度,这是一种基于样本间相似性度量的间接聚类方法,属于非监督学习方法。此算法以k为参数,将n个对象分为k个簇,以使簇内具有较高的相似度,且簇间的相似度较低。相似度的计算根据一个簇中对象的平均值来进行。此算法首先随机选择k个对象,每个对象代表一个聚类的质心。对于其余的每个对象,根据该对象与各聚类质心之间的距离,将其分配到与之最相似的聚类中,然后计算每个聚类的新质心。重复上述过程,直到准则函数会聚。K-means算法是一种较典型的逐点修改迭代的动态聚类算法,其要点是以误差平方和为准则函数。逐点修改类中心:一个象元样本按某一原则,归属于某一组类后,就要重新计算这个组类的均值,并以新均值作为凝聚中心点进行下一次像元素聚类;逐批修改类中心:在全部象元样本按某一组的类中心分类后,再计算修改各类的均值,作为下一次分类的凝聚中心点。

由此便可发现本文算法中所运用的迭代演变局部集群和集群中心的思想实际上是K-means的一个特例。通过使用Eq.(1)的距离计算方法优势,像素搜索可被集中到平面空间的区域内,这与超像素点K的数量成反比。在实际应用中,一个像素点会分布在不超过8个族群中心的局部领域内。同时,还发现在多次迭代后SLIC算法收敛误差急剧降低。实验测试表明,运用该算法需要4～10次迭代,而在文中所有的结果均是以10次迭代的过程得到。

经典的k均值算法时间复杂度为O(NKI),在此N为图像像素点的数量,K是族群的数量,I是为达到收敛所需的迭代次数。由于需要计算从任意一点到不超过8个族群中心的距离外加迭代次数为恒定的,所以SLIC算法的复杂度为O(N)。因此,简单线性迭代聚类SLIC是用于特定超像素分割问题。与K-means不同的是,其避免了一些冗余的距离计算。

3SLIC算法实验测试性能分析

在这一部分,由实验测试所得结果来对超像素分割方法与其他4种最为先进的分割算法进行比较,即GS04[4],NC05[5],TP09[6],QS09[7]。GS04和NC05是基于图论的方法,而TP09和QS09是基于梯度的方法。NC05和TP09被用于产生所需的超像素点数,而GS04和QS09需要调试参数来获得所需的超像素点数。该算法的选择提供了一种较好的先进性代表。

图1中提供了一种与这些算法相对的输出视觉比较。为提供一种定性的比较,运用了细分误差和边界召回衡量方法。

图1　各种分割算法比对

图1中超像素的视觉比较,在所有图像两半中平均超像素点的大小约为100个像素点和300个像素点。每一对行展示了整个分割图像与其中心部分。

图2(a)中为低分割误差值随超像素点数量变化关系的图绘。图2(b)中为边界召回值随超像素点数量变化的关系。NC05的输出视觉上是最佳的但其边界召回较差。GS04的边界召回比其他算法均高,部分原因在于其在对象边界附近放置了诸多分割片。

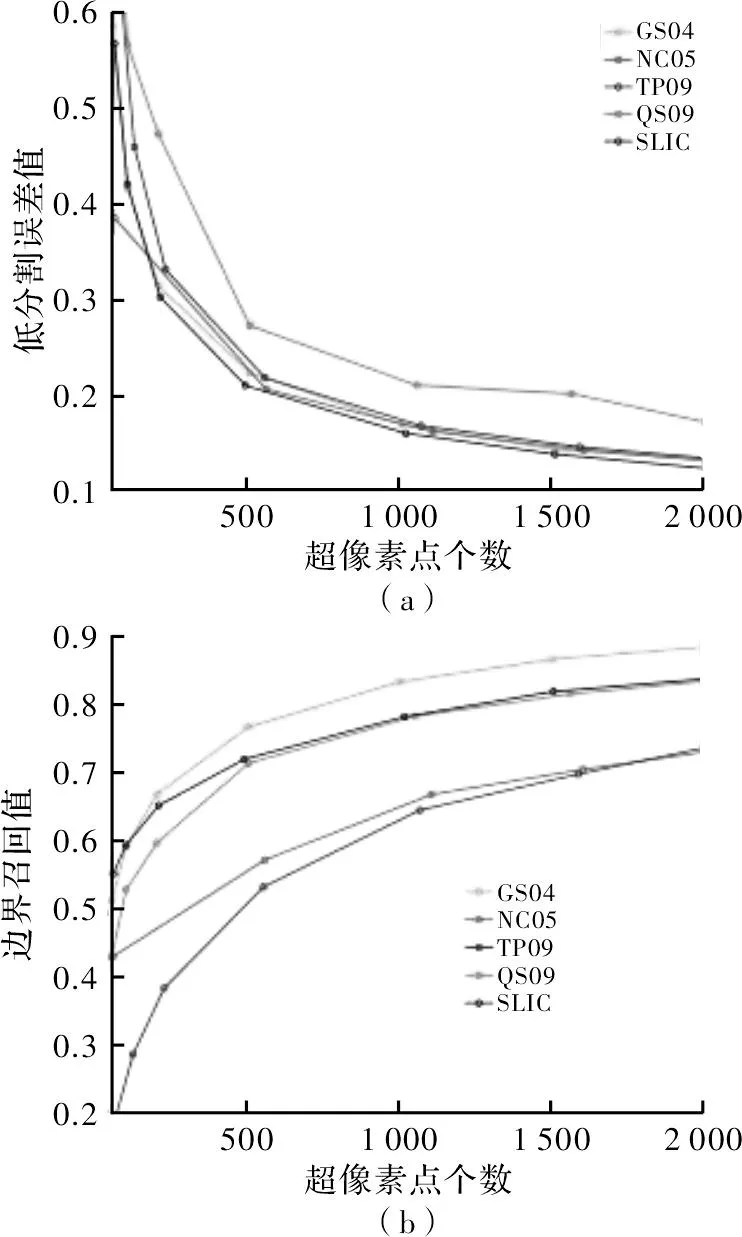
图2　SLIC等算法性能值随超像素点个数变换规律对比图

一种良好的超像素分割算法应有较低的分割误差和较高的边界召回。为使其作为预处理算法有作用,如此的一种分割应产生大小相等、紧凑的、数量受控的超像素。基于同样的原因,该算法应有较低的计算成本,较少的输入参数。图2(b)中表明GS04的召回边界最高,这是因其产生了几个片段,与图2(a)中的对象边界较为接近。然而,从图2(a)中可看出,GS04也表现出了比本文算法更高的低分割误差。从图2(a)中可看出,SLIC算法低分割误差最低。同时由图2(b)可得知,有较高的边界召回。然而,除非执行参数搜索,否则GS04并不会输出所需数量指定大小的超像素点。这需要几次的运行算法,超像素大小不等使得这种算法并不适合基于超像素的应用[8-10]。总之,本文所提出的算法的处理速度比其他先进算法快。同时,能产生与实际所需大小相等紧凑的超像素点。

4结束语

超像素分割算法作为一个预处理步骤来处理诸如对象类识别和医学影像分割是有利的。为实现有用性,这些算法输出的超像素点需紧凑、大小基本相等、质量高、计算开销低。在处理50万像素点以上的图片中,少有算法可以达到这种要求。本文提供了一种新颖的超像素分割算法(SLIC),其复杂度为O(N),输出的超像素点品质高,内存和计算成本较低。只需一定数量的像素点数作为输入参数,计算成本和内存的使用成线性比例增加。可证明该种超像素算法在对象类识别和医学影像分割方面的功效,与其他的先进算法相比,本文SLIC算法可获得更好的品质和更高的计算效率。

参考文献

[1]AnderbergM.Clusteranalysisforapplications[M].Cambridge:AcademicPress,1973.

[2]GeriSchneider,JasonPWinters.用例分析技术[M].师奈德,译.北京:机械工业出版社,2002.

[3]GreenPE,CarmoneFJ,KimJ.Apreliminarystudystudyofoptimalvariableweightingink-meansclustering[C].Paris:Classification,1990.

[4]FelzenszwalbP,HuttenlocherD.Efficientgraph-basedimagesegmentation[J].InternationalJournalofComputerVision,2004,59(2):167-181.

[5]RenX,MalikJ.Learningaclassificationmodelforsegmentation[C].Suzhou:IEEEInternationalConferenceonComputerVision,2003.

[6]LevinshteinA,StereA,KutulakosK,etal.Turbopixels:fastsuperpixelsusinggeometricflows[J].IEEETransportationsonPAMI,2009,31(12):2290-2297.

[7]VedaldiA,SoattoS.Quickshiftandkernelmethodsformodeseeking[C].SaltLake:ComputerVision-ECCV2008,SeriesLectureNotesinComputerScience,2008.

[8]LevinshteinA,SminchisescuC,DickinsonS.Multiscalesymmetricpartdetec-tionandgrouping[C].Shanghai:IEEEInternationalConferenceonComputerVision,2009.

[9]MoriG.Guidingmodelsearchusingsegmentation[C].Tokoyo:IEEEInternationalConferenceonComputerVision,2005.

[10]FulkersonB,VedaldiA,SoattoS.Classsegmentationandobjectlocalizationwithsuperpixelneighborhoods[C].Shanghai:IEEEInternationalConferenceonComputerVision,2009.

中图分类号TP391.41

文献标识码A

文章编号1007-7820(2016)03-039-03

doi:10.16180/j.cnki.issn1007-7820.2016.03.010

作者简介:刘俊(1990—),男,硕士研究生。研究方向:图像分割算法。

收稿日期:2015- 07- 21