联合生产博弈模型

刘歌群,詹志国,胡　琦,吕伟臻

(上海理工大学 光电信息与计算机工程学院,上海　200093)



联合生产博弈模型

刘歌群,詹志国,胡琦,吕伟臻

(上海理工大学 光电信息与计算机工程学院,上海200093)

摘要联合生产领域的背叛通常是合作基础上的背叛,现有的合作博弈模型与非合作博弈模型均不易进行较好地刻画。为此,构建了一个非完全合作的两人博弈模型,用于刻画联合生产时既要偷工减料又不能使联合关系破裂的经济现象。文中给出了基于收益和回报率两个版本的博弈模型,分析了参数对模型特征的影响。基于回报率模型,研究了BA无标度网络上的演化博弈,分析了合作密度对模型参数的依赖关系。揭示了电子联合生产领域偷工减料以次充好的现实问题。

关键词博弈模型;联合生产;收益;回报率

A Joint Production Game

LIU Gequn,ZHAN Zhiguo,HU Qi,LÜ Weizhen

(School of Optical-electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

AbstractExisting cooperative and non-cooperative games cannot satisfactorily describe the defections in joint production because such defections are generally underlain by cooperation.A non-fully cooperative game with two players is constructed to describe the behavior of jerry-builders in joint production.Two distinct versions of the model are given,one based on payoff and the other on rate of profit.The influence of parameters on the model features is analyzed.Based on rate of profit,evolution game on BA scale-free networks is studied and the cooperation density dependence of model parameter analyzed,revealing shoddy social reality in the field of joint production of electronics.

Keywordsgame;joint production;payoff;rate of profit

人类进入科技时代后专业化程度越来越高,分工越来越细,一个产品或者工程需要多个经济主体的协作才能完成。协作者之间为了利益相互合作,合作过程中为了利益又相互竞争或者背叛,因此合作与背叛是经济生活中不变的情节[1-3]。联合生产是若干个企业或个人为了完成某一产品或者工程共同投入人力、设备、场地、信息、渠道与资金的协作行为。联合生产内含了竞争与合作,总产出的共享性会促进合作的产生,而总产出的分享性却会诱使参与人竞相投机,所以联合生产中的背叛较大多是合作基础上的背叛[1],而不是非合作式的背叛。背叛方先采取合作策略赢得机会与资格,然后再通过偷工减料、以次充好或捏造数据等背叛行为攫取目标利润。以次充好的产品、豆腐渣工程以及伪造的业绩等,均是这种背叛现象的例证。当今社会竞争激烈,优势资源与机会短缺,获得资格把握机会成为头等大事,如各种电子联合生产行业。因此,在联合生产博弈中研究这种具有非完全合作性质的背叛行为具有时代意义。

经济主体之间相互协作或者结盟,围绕成本、价格、产量与利润展现的种种行为引起博弈论学者的关注,各种经济博弈模型不断涌现[2-16],如典型的囚徒困境模型[10]、公共品博弈模型[11]及敲竹杠模型[14-15]等。在这些模型对背叛行为有着各种各样的假设。本文构建一种新的联合生产博弈模型,将完全合作定义为合作,而将非完全合作定义为背叛。模型在两个局中人的情境下,考虑背叛方投入成本并分享合作方的利润,同时通过偷工减料压低成本以提高回报率的情况。博弈模型作为复杂网络上的演化博弈的核心环节,分析了合作密度对模型参数的依赖关系。

1博弈模型的构建

文中考虑有两个经济主体参与的非完全合作联合生产,博弈模型结构特征如下:

(1)博弈方(Players)甲、乙两个独立决策的个人或经济主体,联合进行某一产品的生产或者工程的施工;

(2)协议(Agreement)首先给出两个新的成本定义。将完成一项生产任务所应花费的最小成本定义为必要成本,此时按必要成本生产的产品销售额等于成本,企业盈亏平衡。将必要成本之外投入的成本定义为盈利成本,包含了盈利成本的产品其销售额大于必要成本与盈利成本之和。利润除以盈利成本定义为盈利成本利润系数,其中利润等于销售额减去总成本,即必要成本与盈利成本之和。将总成本归一化为1,假设每一方的必要成本为c,0≤c≤1,产品盈利成本利润系数为k。协议规定双方各按必要成本与盈利成本即总成本1进行生产,联合生产产品的销售额均分;

(3)策略(Strategies)每个博弈方各有两种策略,合作(Cooperation,C)时按总成本1进行生产,背叛(Defection,D)时偷工减料按必要成本c进行生产,出资矩阵见表1;

表1　出资矩阵

(4)得益(Payoffs)设p为双方总出资额,则产品总销售额为2c+(p-2c)(k+1),利润为(p-2c)k。因背叛方的偷工减料是私下行为,不为对方所知,双方按约定均分销售额c+0.5(p-2c)(k+1),各得到销售额。结合4个不同的策略组合,减去出资后,得到收益矩阵如表2所示。

表2　收益矩阵

2回报率矩阵

按惯例,文中将双方合作时每一方的收益用R表示,一方合作一方背叛时合作方的收益用S表示,一方合作一方背叛时背叛方的收益用T表示,双方背叛时每一方的收益用P表示。当0R>P>S,双方合作时都产生盈利,R>0。(C,D)或(D,C)时C方收益为负而D方收益为正,双方一盈一亏,背叛方通过压缩成本侵占了合作方的利润,而合作方因为投入了盈利成本亏损。这种情况在现实中难以为继,生产联合会在一次合作后破裂。本文关注能长期联合的情况,即k>1,满足合作方保本条件的博弈。

k>1时,R>T,(C,C)是纳什均衡,背叛行为不应当出现。可现实中,联合生产双方压缩成本偷工减料的行为比比皆是,因此需要寻找背叛方的诱惑来源。众所周知,与利润相比,企业股东或者投资人更关注回报率,最终决定资金流向的是回报率和盈利能力。把表2中各方收益除以对应成本后得到回报率矩阵,如表3所示。

表3　回报率矩阵

参考惯例,文中将(C,C)时各方的回报率用R表示,(C,D)或(D,C)时C方的回报率用S表示,D方的回报率用T表示,(D,D)时各方的回报率用P表示,有P≡0。回报率矩阵与收益矩阵相比,参数c,k相同时策略组合之间的优劣对比不同,模型的性质因之不同。本文所提联合生产模型因此有两个版本,即基于收益的模型和基于回报率的模型。

3回报率对参数的依赖性分析

由以上分析可知,k>1时,从收益的角度而言模型具有合作博弈的性质,而从回报率的角度来说,模型的属性取决于自由参数c和k的取值。在此,以0≤c≤1和1≤k≤3为变化范围,分析回报率对两个自由参数c和k的依赖性。

3.1R对参数的依赖性

由R=(1-c)k,在c-k平面上绘制R的函数图像,用颜色表示R的大小,如图1所示。

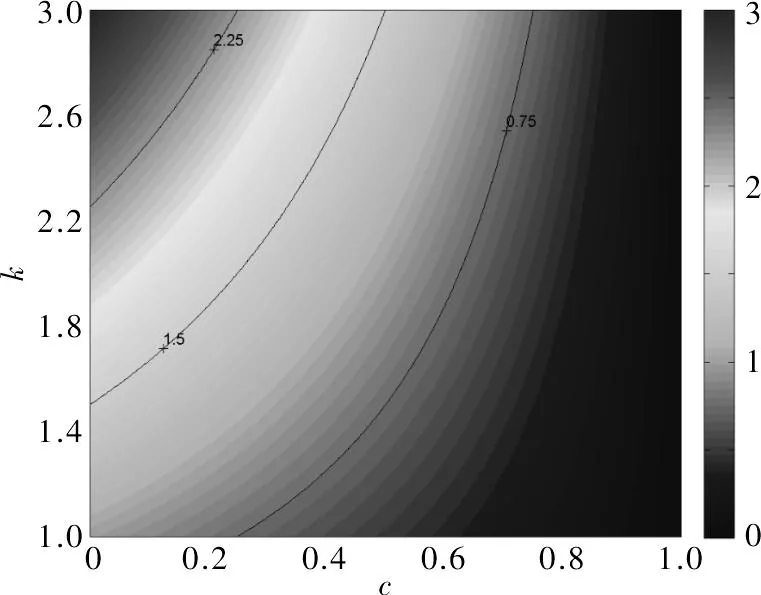
图1　回报率R函数图像

由函数关系及图像可知,R分别与c,k呈正比例关系,与c负相关,与k正相关。k=1时,R≠0,只有在c=1无盈利成本时,才有R=0。在参数变化范围内,R的最小值为0,最大值等于k的最大值。在图上绘制等回报率曲线,可发现为围绕着左上角的弧线。可看出,对于给定的回报率,k与c之间呈反比例关系,且正相关。R的等回报率曲线方程为

(1)

3.2S对参数的依赖性

图2　回报率S函数图像

(2)

3.3T对参数的依赖性

由于0≤c≤1和k≥1,根据函数关系及图3可知,T与k呈正比例关系且正相关,与c呈反比例关系且正相关。T与R相似,在k=1时,T≠0,只有在c=1没有盈利成本时,才有T=0。在参数变化范围内,T的最小值为0,但当c→0时T→+∞,即背叛方遇到了“无本万利的好事”,回报率无穷大。在图上绘制等回报率曲线,可发现为围绕着左上角的弧线。对于给定的回报率,k与c之间呈正相关的非线性关系:(D,C)或(C,D)下C方若要取得一定的回报率,所联合生产的产品必要成本若c越高,盈利成本利润系数k则应当越大。这一基本趋势与R和S是相同的,T的等回报率曲线方程为

(3)

4BA无标度网络上的演化博弈

基于联合生产博弈模型,研究了BA无标度网络上的演化博弈。复杂网络上的演化博弈是博弈模型,网络模型与策略更新规则3个方面相互交织的一个复杂问题,每一个维度的革新都为网络演化博弈带来了丰硕的成果。博弈模型是网络演化博弈的核心环节,反映了自私个体之间的合作竞争关系,能够较好地刻画生物系统中生物体之间的相互作用关系及演化动力学。

本文中,网络节点数N=500,参与者占据在BA无标度网络节点上,网络平均度为3。在每一回合中与其的邻居进行博弈并计算回报率。每个参与着的回报率为与所有邻居博弈的回报率和取平均值。每轮博弈后,要根据模仿规则对网络上的节点的策略进行更新,这里选用的模仿规则为一个考虑到非理性因素的规则,即

(4)

式(4)中,κ噪声水平,其刻画的是个体进行策略更新时随机不确定因素的大小,本文中κ=0.1。Ri,Rj分别为节点i,j的平均回报率。本文的合作密度由最后1 000蒙特卡罗步(蒙特卡罗步取5 000)的平均值取得,所得结果都是经过10次的系综平均。图4为BA网络上合作密度随成本利润系数k变化的函数关系。如图4所示:(1)随着k的增大,合作比例增大;(2)必要成本c增大,合作比例逐渐变大。因此,联合生产者之间的合作关系依赖联合生产模型参数。

图4　BA网络上合作密度随k变化的曲线关系

5结束语

本文针对经济活动中偷工减料压低成本以谋取利益的现象,在两个局中人的情境下,通过将完全合作定义为合作,将非完全合作定义为背叛,构建了一种新的联合生产博弈模型。该模型有基于收益和基于回报率两个版本,分别对应博弈方权衡利弊的不同立场。文中分析了两个版本模型的特征对参数变化的依赖性,以及基于回报率模型,研究了BA无标度网络上的演化博弈。

所提模型对联合生产领域经济现象的分析具有理论意义和现实意义:(1)刻画了合作基础上的背叛,更符合时下偷工减料以次充好之风盛行的社会现实;

(2)基于回报率的模型分析的是相对量形式的收益,更符合投资人的利益;(3)模型属性对参数的依赖性揭示了“偷工减料与诚信生产谁更有利取决于所生产的产品”这一经济规律;(4)可利用复杂网络上的演化博弈研究来提高个体间的合作水平,有助于各部门及时采取所示来抑制电子联合生产行业偷工减料现象。

参考文献

[1]胡晓鹏.不同产权安排下联合生产决策的比较研究[J].数量经济技术经济研究,2005,22(2):33-41.

[2]张维迎.博弈论与信息经济学[M].上海:上海人民出版社,2004.

[3]谢识予.经济博弈论[M].3版.上海:复旦大学出版社,2007.

[4]熊启滨,胡放之.合作与非完全合作博弈理论研究综述[J].三峡大学学报:人文社会科学版,2009,31(3):80-83.

[5]王龙,丛睿,李昆.合作演化中的反馈机制[J].中国科学:信息科学,2014,44(12):1495-1514.

[6]Matjaž Perc,Jesús Gómez-Gardeňes,Attila Szolnoki,et al.Evolutionary dynamics of group interactions on structured populations:a review[J].Journal of the Royal Society Interface,2013,10(80):1-9.

[7]György Szabó,Gábor Fáth.Evolutionary games on graphs[J].Physics Reports,2007,446(4-6):97-216.

[8]邱言玲.最大延迟排序的两人合作博弈[J].电子科技,2015,28(3):72-75.

[9]徐富盛,尚绪凤,许丁丁,等.基于二人零和博弈的商业竞争模式分析[J].电子科技,2013,26(11):1-3.

[10]Hayrdin G.The tragedy of the commons[J].Science,1968,162(3859):1243.

[11]Nunn,Geoffrey E,Watkins,Thayer H.Public goods games[J].Southern Economic Journal,1978,2(45):598-606.

[12]陈长彬,陈泉,盛鑫.供应链合作关系稳定性的博弈分析[J].工业技术经济,2015(2):55-62.

[13]邹晓虎,田金信,周爱民.总承包企业和集群伙伴人群博弈的研究[J].数量经济技术经济研究,2003(8):87-90.

[14]Evans,Howie.Owners,players holding up benefit games for rwanda relief[J].New York Amsterdam News,1994,43(85):56-59.

[15]Luciano Andreozzi.Property rights and investments:An evolutionary approach[J].Games and Economic Behavior,2012,74(1):1-6.

[16]杨晓林.建设项目总承包商与分包商合作关系的单期博弈分析[J].工程管理学报,2010,24(5):545-549.

中图分类号F224.32

文献标识码A

文章编号1007-7820(2016)03-001-04

doi:10.16180/j.cnki.issn1007-7820.2016.03.001

作者简介:刘歌群(1974—),男,博士后,讲师,硕士生导师。研究方向:计算机控制,复杂网络同步与演化博弈。詹志国(1988—),男,硕士研究生。研究方向:复杂网络演化博弈。

基金项目:沪江基金资助项目(C14002);上海理工大学光电信息与计算机工程学院教师创新能力建设基金资助项目(GDCX-Y-1212);上海市研究生创新基金资助项目(JWCXSL1402);2014年上海市大学生创新创业训练计划基金资助项目(SH2014036)

收稿日期:2015- 07- 18