基于改进粒子群算法的平行度误差评定*

周东栋，樊　军

(新疆大学 机械工程学院，乌鲁木齐　830047)



基于改进粒子群算法的平行度误差评定*

周东栋1，樊军2

(新疆大学 机械工程学院，乌鲁木齐830047)

摘要：目前最小二乘法普遍应用于误差评估，但其只适应于精度要求比较低的场合，且用最小二乘法只能是对形位误差的近似计算，误差值不是唯一的。为了精确的评估平行度误差，根据新一代GPS标准，建立了符合最小区域条件的平行度误差评定数学模型。针对平行度误差评定特点，采用一种动态改变惯性权重的自适应粒子群算法，来实现误差的优化评定。最后通过平行度的典型实例来验证该方法的可行性和有效性。

关键词：新一代GPS；最小区域；平行度；惯性权重；自适应粒子群优化算法

0引言

由于平行度误差对机械零部件的综合性能及质量有着重要的影响，对于零部件平行度的检测也显得尤为重要，因此，如何精确地评估平行度误差就有着重要的现实意义。

由于传统的测量误差方法已经无法满足现代制造业的发展要求，因此，以计量数学为基础的新一代GPS标准体系的出现，在一定程度上解决了形位误差的规范评定问题。

由于最小二乘法计算简单便捷，因此到目前为止该方法是评定误差时应用最广泛的一种，但也只能得到近似结果。最精确评定误差的方法是最小区域法，所求得的误差值最小并且唯一，且其实际属于最优化问题[1]。故文中以线对面的平行度为例，根据新一代GPS标准体系的规定，运用一种动态改变惯性权重的自适应粒子群优化算法，按最小条件评定原则对平行度测量数据进行评定。

在运用改进粒子群算法的过程中，惯性权重值随粒子的目标函数性质及位置而改变，引入动态改性权重后的改进算法使收敛速度显著加快，而且可以在一定程度避免陷入局部最优解。

1平行度误差评定数学模型

1.1建立基准平面

根据新一代GPS标准体系的综合模型，为了满足产品的规范和测量评定方法的一致性需求，则需要由不同规范的操作以及算子来实现。其中操作由要素和评估操作组成，而要素操作又由分离、提取、滤波、拟合、集成、构建六类组成[2-3]。

在评定过程中，误差基准要素的评定是关键，由于基准不是理想要素，故可采用分离、提取等操作对误差基准进行分析研究，使基准理想化。由于最小区域法所得的包容区域平面是拟合基准平面方法里最接近实际平面的一种，因此一直以来有很多学者投身于此方面的研究。

由平面度的定义可知，平面度误差就是被测的实际平面相对于基准平面的最小变动量。这里，我们首先将评定平面度误差转换为求理想平面的方位。设点pi(xi,yi,zi)(i=1,2,…,n)是空间基准实际平面上的测量点，计算点pi(xi,yi,zi)到理想平面的距离，如果满足平面内包容所有点距离的最大与最小值的差值为最小，那么所求平面度的误差值即等于此距离的差值，该平面即为所要求得的基准平面，如图1所示。

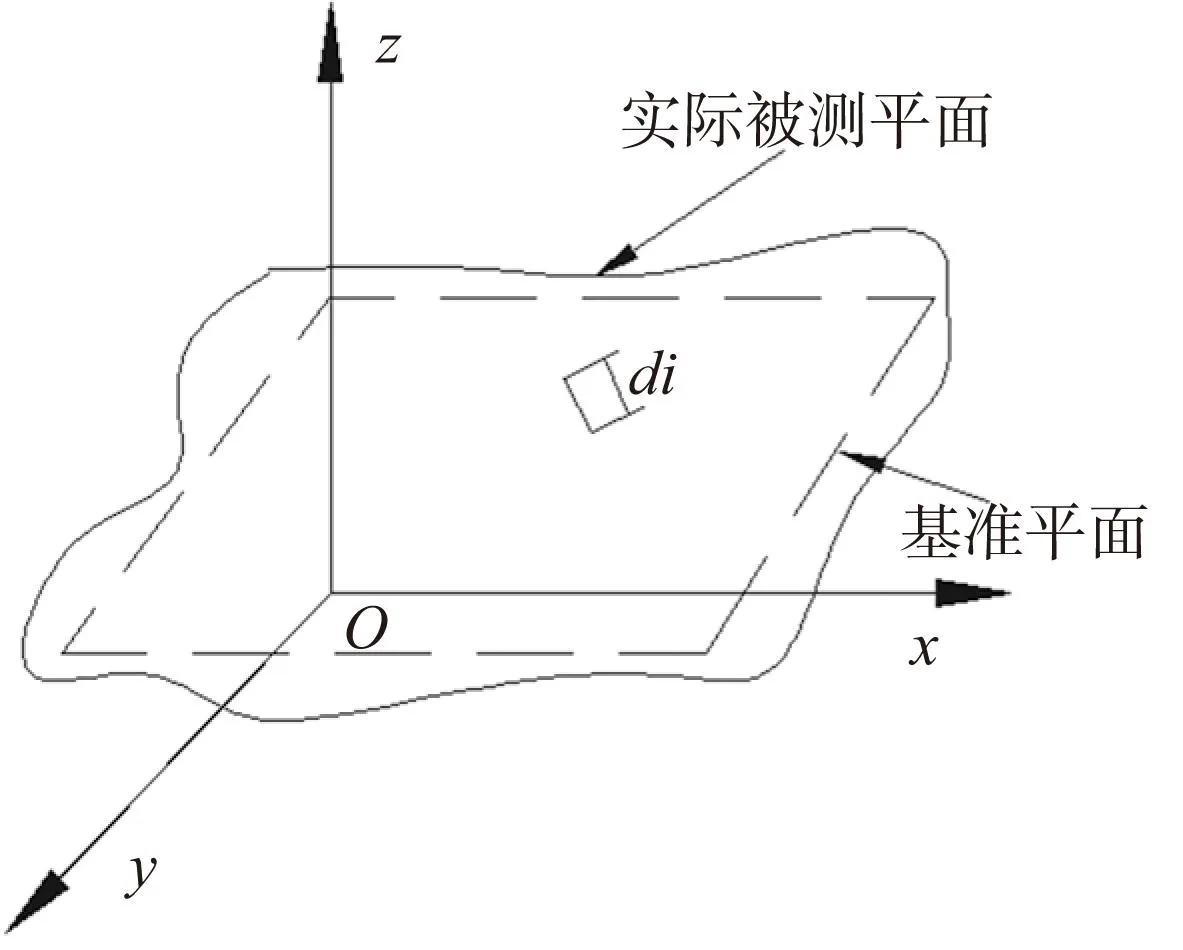
图1　被测与基准平面

设基准平面拟合方程为：

lx+my+nz+h=0

(1)

其中l,m,n,h为待定系数，被测轮廓上各点到此平面距离为di：

(2)

平面度误差即为：

f(l,m,n)=dmax-dmin

(3)

将函数f进行优化使其最小，此时就将求最小条件的平面问题转变成求l、m、n值的问题，进而可以得到基准平面拟合方程。

1.2线对面定向误差的评定数学模型

取基准平面上任意点P0(X0,Y0,Z0)为原点，建立新坐标系(O,X,Y,Z)，并使ox∥OX，XOY坐标平面与xoy坐标平面的夹角为α，如图2。

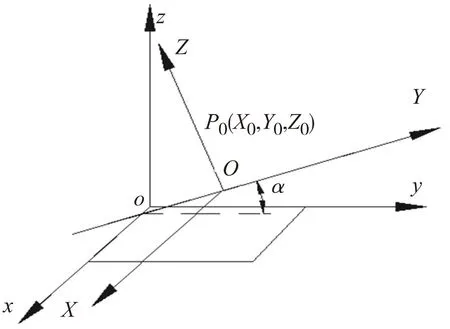
图2　空间坐标转换

对于原坐标系(o,x,y,z)与新坐标系(O,X,Y,Z)之间的坐标变换公式如下所示：

(4)

对被测点pk(xk,yk,zk)(k=1,2,…,n)，通过上式进行变换得到相应点Pk(Xk,Yk,Zk)(k=1,2,…,n)。被测直线测点集算术平均中心点的坐标为P0(X0,Y0,Z0)，其中，

(5)

在此引入文献[4]中的误差理论和最小区域原理，可以得知其理想直线就是以被测直线的测点集算术平均中心点为基点的最小区域的拟合直线。设该直线的方向向量为S={p,q,r}，则以P0(X0,Y0,Z0)为基点的最小区域拟合直线L方程为：

(6)

任意测量点Pk(Xk,Yk,Zk)到直线L的距离D为：

D=

(7)

依据直线度定义可知，直线度的误差为：

f1(p,q,r)=Dmax

(8)

对式(7)进行优化分析，获得最大值，带入式(8)进行收敛优化得到最小条件，便可求得满足最小区域条件拟合直线的p、q、r值。

由于在任意方向上线对面倾斜度的误差包容区域实际上是以其拟合直线为轴线的并且包容了所有误差测量点的一个理想的圆柱面，则此理想包容圆柱面的直径就是倾斜度的误差值，即：

(9)

平行度以及垂直度误差则可被看作是当理想正确角度分别为0°和90°时线对面倾斜度误差的两种特殊的情况。因此，适当改变理论正确角度就可以进行平行度和垂直度的评定计算。

2改进粒子群优化算法

2.1粒子群优化算法

PSO是从鸟的种群行为的特性受到启发，并对鸟群捕食的过程进行仿真研究，通过群体中个体之间的协调和信息共享，进而取得最优解[5]。

假定目标搜索空间为D维，由n个粒子组成初始种群，粒子i(i=1,2,…,n)的位置表示为xi，粒子i(i=1,2,…,n)的速度表示为vi。n个粒子都可以找到与之相对应的适应值，在找到两个最优解后的粒子i可以按照如下公式进行更新各自的速度与位置[6]：

(10)

(11)

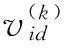
随着粒子群优化算法的出现，国内外的学者给予了极大的关注，并提出了许多改进优化算法，对于参数惯性权重的改进就是一种重要的改进。后来国外学者Shi和Eberhart在标准化公式中引进了惯性权重因子w(w≥0)进行了改进，修改后的为的公式如下[7]：

(12)

2.2一种动态改变惯性权重的自适应粒子群算法

根据文献[8]中平均聚集距离和最大聚焦距离的定义内容可知：

(13)

(14)

其中m为粒子群的粒子数；d为每个粒子的维数；pid为群体当前搜索到的最佳位置；xid为个体粒子当前观测到的最佳位置。

定义粒子当前的聚焦距离的变化率为：

(15)

在每一次的迭代过程中，首先通过计算得到本次迭代得到的平均聚焦距离和最大聚焦距离，根据上式所得到的聚焦距离的变化率值的大小就可以相应地调整惯性因子w。

基本的PSO算法可被看作是在w=1的情况下，w取适当的数值，较大的w可以加强全局搜索能力，而较小的w则可以加强局部搜索能力，w执行了平衡两者之间的关系的作用，进而使之达到最优的平衡状态，同时也可根据每一次迭代计算过程的不同时期的搜索情况适当地调整w的数值。在此列出一种自适应的非线性惯性权值递减函数，表达式如下所示[9]：

(16)

其中α1=0.3，α2=0.2，r为一个随机数并且其取值范围在[0,1]之间。该方法是随机地选取w值并且使w随着聚焦距离变化率的变化适当地自我调整，使其更好地适应实际情况，从而更加机动地调整全局和局部搜索能力。从式(15)中分析可知当其聚焦距离的变化率值比较大时，最大和平均的聚焦距离差异也比较大，则此时粒子的全局搜索能力较差，因此要进行调整使粒子可以快速地进入全局搜索，反之，则应当提高粒子的局部搜索能力。

该方法(算法DCWPSO)的具体实现步骤为[7]：

Step1：初始化一群粒子(群体规模为n)包括随机位置和速度。

Step2：设置粒子的当前位置是pi，初始粒子群中最优粒子的位置是pg。

Step3：根据收敛准则判断算法能否满足，如果满足条件，则转Step5；否则，接着执行Step4。

Step4：针对粒子群中的所有粒子，进行如下操作步骤：

①通过式(10)、(11)、(12)更新粒子的速度以及位置；

②通过式(13)、(14)、(15)计算出聚集距离的变化率，进而确定惯性权重w的值。

Step5:输出pg，算法运行结束。

3实例验证与结果讨论

线对面平行度误差的传统测量方法如图3所示，在轴线对面的平行度评定中，在被测孔内插入适当的心轴，将心轴用来模拟被测轴线(当允许排除形状误差时)，将基准平面放置在平板上，在被测心轴上的两测点距离为L2的位置上分别测得读数为M1、M2，由于线对面的平行度误差为：

(16)

据此可以测得平行度：Δ=0.046mm。

但是传统的测量方法操作繁琐，测量精度低，人为影响因素比较大，存在原理误差—心轴自身的形状误差影响最终的测量结果。

图3　传统测量方法

故本试验采用三坐标测量机进行测量，将被测箱体零件放在工作台的任意位置，然后建立测量坐标系，手动测点，在数据处理系统中提取被测点坐标。表1为文献[10]中给出的如图4所示的被测箱体零件上直径为φ24的孔的轴线对基准面A的平行度误差的测量数据。

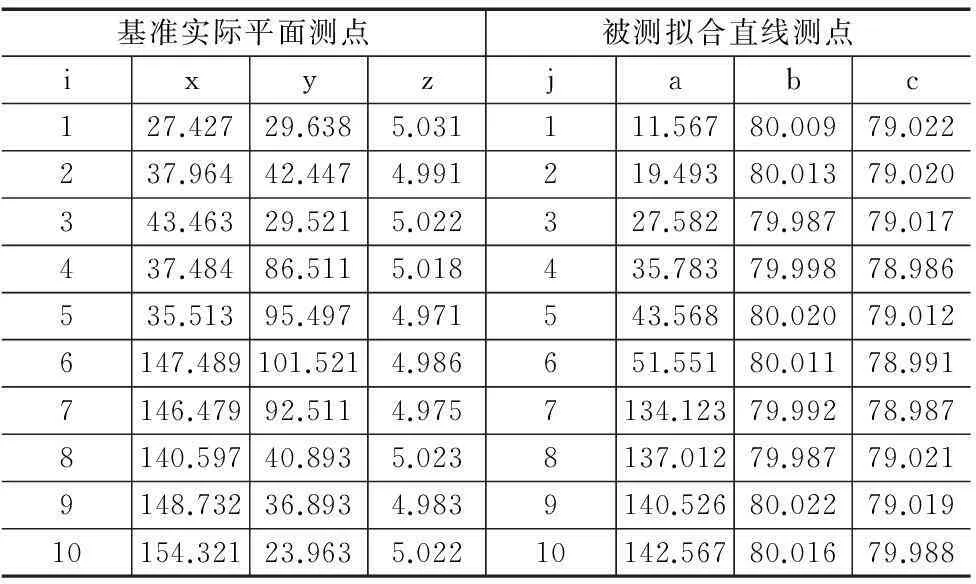
表1　被测箱体零件平行度数据(单位：mm)

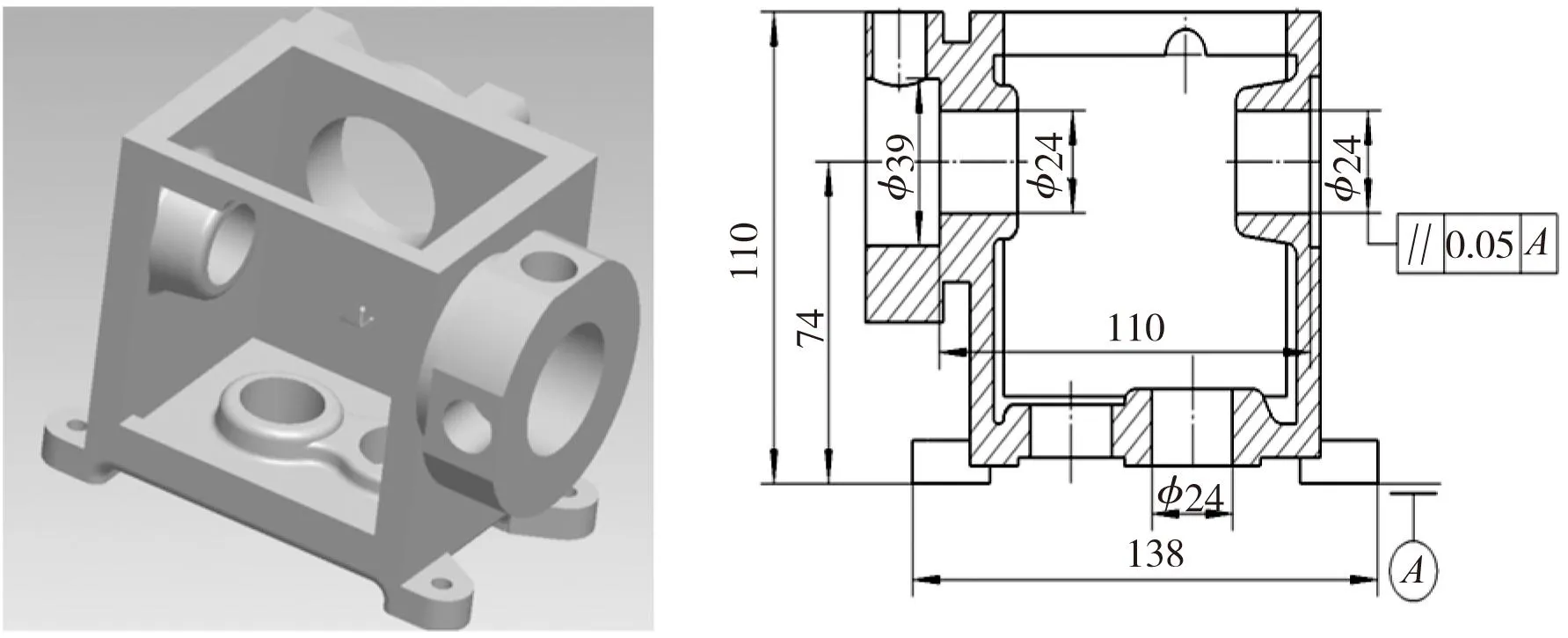
图4　三维图和平面尺寸图

根据之前分析所得到的优化算法进行分析计算。将三种误差的评定方法的计算结果做如表2所示比较。

表2　评定结果比较

图5为计算数据时DCWPSO算法的粒子适应度收敛曲线，由图分析可知，其收敛速度非常快，且收敛过程也比较稳定。

图5　粒子适应度收敛曲线

4结束语

本文在新一代GPS操作的基础上，为了可以有效地解决误差评定中非线性的优化问题。通过建立基于了满足最小条件的平行度误差评定的数学模型以及优化目标函数，应用了一种如公式12所示的动态地改变惯性权重的自适应粒子群算法，进一步实现了线对面的平行度误差的评定。通过表2结果比较可知该理论方法比最小二乘法和传统方法计算的结果评定精度更高，在理论上更加接近真实值。

[参考文献]

[1] 黄富贵.平面度误差各种评定方法的比较[J]. 工具技术，2007，41(8)：107-109.

[2] 蒋向前.新一代GPS标准理论与应用[M]. 北京：高等教育出版社，2007.

[3] 马利民.新一代产品几何量技术规范(GPS)理论框架体系及关键技术研究[D]. 武汉:华中科技大学，2006.

[4] 费业泰.误差理论与数据处理[M]. 北京：机械工业出版社, 2005.

[5] Kennedy J, Eberhart R. Particle swarm optimization[C] // Proceedings of IEEE International Conference on Neural Networks. Piscataway：IEEE Service Center，1995：1942-1948.

[6] 张顶学，关治洪，刘新芝.一种动态改变惯性权重的自适应粒子群算法[J]. 控制与决策，2008，23(11)：1253-1257.

[7] 杜振鑫，王兆青.一种改进的动态改变惯性权重的粒子群算法[J]. 微电子学与计算机，2011，28(3)：85-88.

[8] 李宁，孙德宝，岑翼刚,等.带变异算子的粒子群优化算法[J]. 计算机工程与应用,2004(17)：12-13.

[9] 任子晖，王坚.一种动态改变惯性权重的自适应粒子群算法[J].计算机科学，2009，36(2)：227-229.

[10] 高明，鲍家定，周晴伦.基于粒子群算法的线对面的垂直度误差评定[J].中小企业管理与科技(上旬刊)，2012(6): 203-205.

(编辑赵蓉)

Parallelism Error Evaluation Based on an Improved Particle Swarm Optimization

ZHOU Dong-dong1，FAN Jun2

(College of Mechanical Engineering, Xinjiang University, Urumqi 830047,China)

Abstract：Currently Least Square Method (LSM) is commonly applied in the error evaluation, but it is adaptive to the condition of low accuracy requirement. Besides, the error value obtained by LSM is not the minimum. In order to accurately evaluate parallelism error, a minimum zone mathematical model for the parallelism error evaluation was given based on the new generation GPS standards．According to the characteristics of parallelism error evaluation，a new adaptive Particle Swarm Optimization algorithm with dynamically changing inertia weight (DCWPSO) is proposed to implement optimization in the error evaluation．Finally，an example was given to illustrate the proposed method.

Key words：the new generation GPS；the minimum zone method；parallelism；inertia weight；adaptability particle swarm optimization

中图分类号：TH16；TG506

文献标识码：A

作者简介：周东栋(1991—)，男，河南邓州人，新疆大学硕士研究生，研究方向为人体外骨骼的设计与研究，(E-mail)13134462601@163.com;通讯作者：樊军(1965—)，男，山东青岛人，新疆大学副教授，研究方向为人体外骨骼的设计与研究，机械零件误差分析，(E-mail)xj_fanjun@163.com。

*基金项目：国家自然科学基金项目(11462021)

收稿日期：2015-08-06

文章编号：1001-2265(2016)02-0108-04

DOI:10.13462/j.cnki.mmtamt.2016.02.031