基于五次多项式插值的大惯量弱刚性回转系统的启动速度控制

陈爱波，陈五一

(北京航空航天大学 机械工程及自动化学院,北京　100191)



基于五次多项式插值的大惯量弱刚性回转系统的启动速度控制

陈爱波，陈五一

(北京航空航天大学 机械工程及自动化学院,北京100191)

摘要：用于支撑大型目标进行360°方位电磁测试的回转支撑系统具有大惯量弱刚性的特点，为满足系统在较短时间内由静止加速到测试转速0.1°/s所引起的待测目标的转速超调量不大于0.001°/s，提出利用单段五次多项式对整个加速过程进行速度插值的控制算法，不仅保证速度和加速度全过程连续可导，而且加加速度始终连续变化。与S形加减速控制算法相比，该算法更加简便且使系统具有更高的柔性，通过利用ADAMS对回转支撑系统进行刚柔耦合动力学仿真验证了该算法的优越性。

关键词：五次多项式; 大惯量弱刚性;速度控制

0引言

在微波暗室中对大型目标进行360°方位电磁性能测试需要专门设计的回转支撑系统，但为减小支撑构件的外形尺寸对电磁测试的影响，数控回转台面与待测目标之间只能采用长径比很大的柱形钢作为联接支撑杆，使得该支撑系统在转动过程中具有大惯量弱刚性的特点。虽然预定的目标测试转速只有0.1°/s，但要求回转系统由静止加速到测试转速所引起的目标转速超调量不大于0.001°/s，即要求系统启动过程足够平稳无冲击。

在数控领域，加减速控制方法一直是研究热点。直线加减速和指数加减速控制方法[1-2]在传统数控系统中应用较多，算法简单，但在加减速过程中存在加速度突变，速度过度不平滑。以七段S曲线为典型的S形加减速控制方法[3-4]虽然能实现连续的加速度，有效减小柔性冲击，但其加加速度存在阶跃变化的不连续点，仍会导致系统加减速过程中存在冲击和振动，虽然很多研究[5-7]对传统S形加减速控制算法进行改进使其加加速度没有突变，但该类算法本身分段复杂，或涉及参数较多，程序实现繁琐。三次多项式加减速控制方法[8]采用单段三次多项式分别插值加减速段，算法简单易实现，保证了加加速度在变速运动阶段的连续，但在加减速段与匀速段的衔接点处仍是阶跃变化的。三角函数法[9]的思想与三次多项式法相似，且可以实现加加速度的连续变化，但计算复杂。

为尽量减小回转支撑系统启动时的冲击和振动，本文提出基于五次多项式插值的速度控制算法，保证系统启动过程中加加速度始终连续变化，有效提高系统的柔性。

1五次多项式速度插值算法

1.1基于五次多项式插值的启动速度控制算法

图1　回转系统启动过程角速度变化曲线

系统正常启动的过程一般是由静止状态逐渐加速到工作速度后保持匀速运动，而由静止到工作速度的速度变化过程即是对启动速度的控制过程。传统启动过程多采用匀加速运动，即速度为斜坡变化，而基于五次多项式插值的启动速度控制算法即是以单段五次多项式代替斜坡输入，以加速启动过程的初始点和终止点的运动状态作为插值的边界条件，对整个加速过程进行速度插值，如图1所示。

对于回转系统，角速度曲线的五次多项式构造函数可写为如下形式：

ω(t)=a5t5+a4t4+a3t3+a2t2+a1t+a0,t∈[0,tm]

(1)

其中，tm为加速过程所需时间。对式(1)依次求导可分别得到角加速度ε、角加加速度j的曲线函数分别为：

(2)

为保证启动过程中角速度、角加速度的平滑过渡及角加加速度的连续变化，插值函数需要满足以下边界条件：

(3)

式中，ωm为加速过程结束时的角速度，即回转系统正常工作转速。

将上述边界条件代入式(1)、(2)中，可得到用于求解插值多项式系数的线性方程组如下：

(4)

易求得多项式系数为：

(5)

将式(5)代入式(1)、(2)便可得到回转系统基于五次多项式插值的启动速度控制算法的角速度、角加速度、角加加速度曲线函数分别为：

(6)

1.2五次多项式加减速控制模型

五次多项式插值应用于回转系统启动速度控制是为保证系统平稳无冲击启动，基于相同原理，五次多项式速度插值算法同样适用于一般数控系统实时加减速控制，以更加简便的控制算法满足柔性控制的需求。

基于五次多项式插值的加减速控制过程即是以两个单段五次多项式分别作为加速段和减速段的速度插值函数，如此，整个加减速过程只分为三段：五次多项式加速段、匀速段、五次多项式减速段。对于加减速段，由于速度曲线函数可以沿时间轴平移，因此在求解加减速段曲线函数时，均可将该段起始时间看作t0=0，加速或减速过程所需时间为tm，则该段的速度曲线函数即可表示为如下一般形式：

V(t)=a5t5+a4t4+a3t3+a2t2+a1t+a0,t∈[0,tm]

(7)

相应地，加速度A、加加速度J曲线函数分别为：

(8)

对式(7)积分可得位移曲线函数为：

S(t)=a5t6/6+a4t5/5+a3t4/4+a2t3/3+a1t2/2+a0t

(9)

五次多项式加减速控制模型中位移、速度、加速度及加加速度曲线如图2所示。

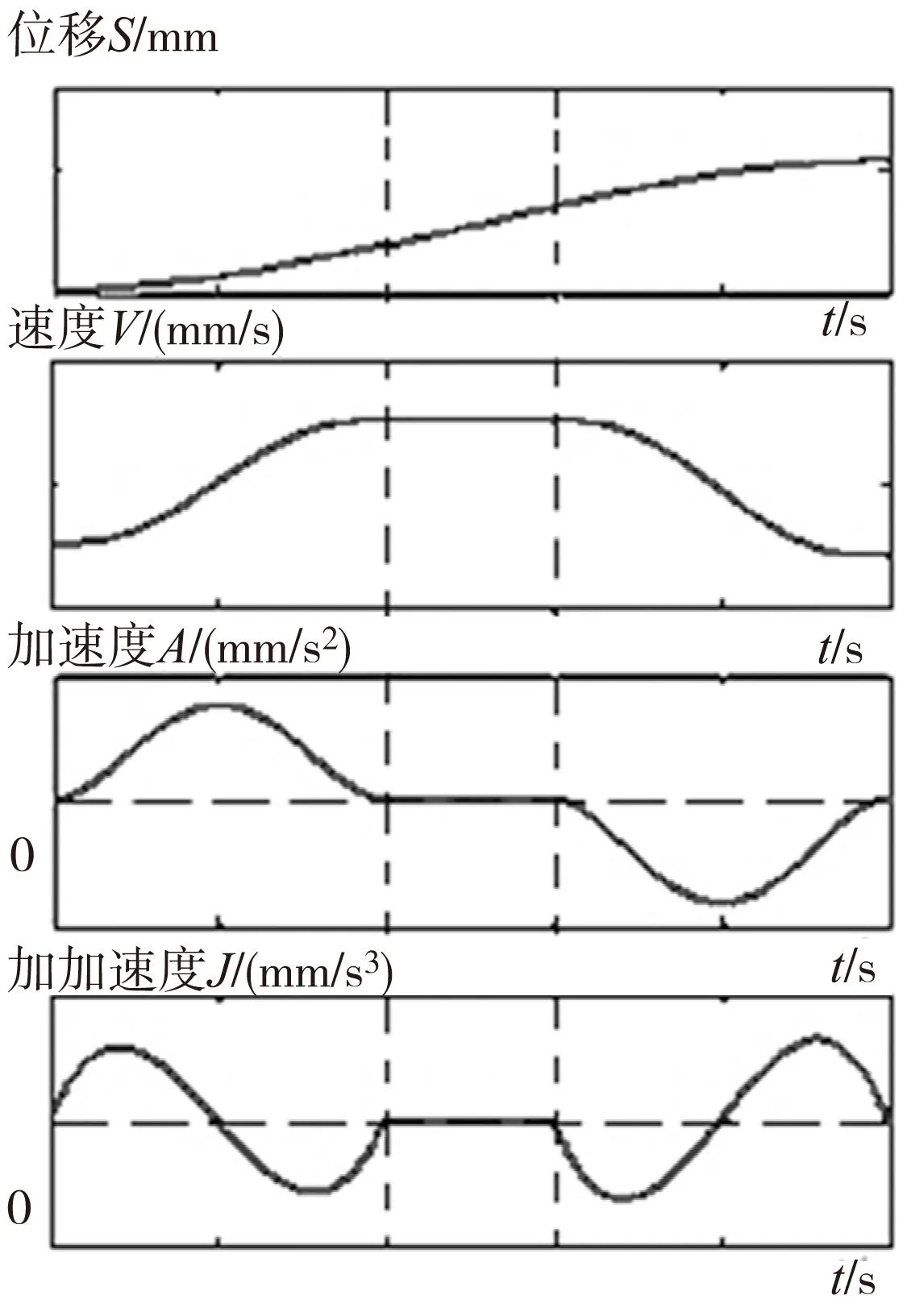
图2　五次多项式加减速控制模型

对于加速段或减速段的插值函数，为保证全过程加加速度连续变化，需满足的边界条件为：

(10)

式中，v0、vm分别为加速或减速过程的始、末速度。

将上述边界条件代入式(7)、(8)中，可得到用于求解插值多项式系数的线性方程组如下：

(11)

易求得多项式系数为：

(12)

将以上求得的多项式系数代入式(7)、(8)便可得到加减速段以t0=0作为初始时刻的插值函数，对于全过程的绝对插值函数只需要对自变量t进行平移即可得到，不在此详述。

2ADAMS动力学仿真验证

随着ADAMS版本的改进，在ADAMS中直接建立柔性体或将刚体创建为柔性体的方法变得更加简便和完善，对于含柔性体的一般动力学分析基本无需借助于外部有限元软件[10-12]。

如图3所示，在ADAMS中首先建立约束完整的回转支撑系统刚体模型，并将待测目标的质量、质心位置及转动惯量按照实际目标的参数进行设置，同时保证两个支撑杆的尺寸及材料属性与实际设计相同，以保证仿真结果的有效性，然后直接利用ADAMS的刚体柔性化功能将两支杆创建为柔性体，可采用默认的线性四面体单元等设置，最后，对数控转台施加转动并设置为转速控制。

图3　基于ADAMS的回转支撑系统刚柔耦合模型

分别采用分段S形曲线插值和五次多项式插值对数控转台加速启动过程进行速度控制，均使系统在13s内由静止加速到测试转速0.1°/s，同时检测待测目标的转速变化。在ADAMS中，分段S形曲线插值算法的控制语句为：

IF(time-6.5:0.2d*time**2/169,0.05d,

IF(time-13:0.1d-0.2d*(time-13)**2/169,

0.1d,0.1d))

五次多项式插值算法的控制语句为:

IF(time-13:0.6d*time**5/13**5-

1.5d*time**4/13**4+

1d*time**3/13**3,0.1d,0.1d)

设置仿真时长50s、步长0.01s，采用动力学仿真模型，得到基于两种控制算法的转台角速度、角加速度控制曲线及待测目标角速度变化曲线分别如图4、图6所示，其中，系统加速过程结束前后的一段时间内目标角速度变化曲线分别如图5、图7所示。

分析仿真结果可以看出，系统经过相同时间加速到相同的转速，采用分段S形曲线速度控制算法引起的目标转速超调量为0.0015°/s，而五次多项式速度控制算法引起的超调量为0.001°/s，验证了基于五次多项式插值的速度控制算法在提高系统柔性减小加减速冲击方面的优越性。

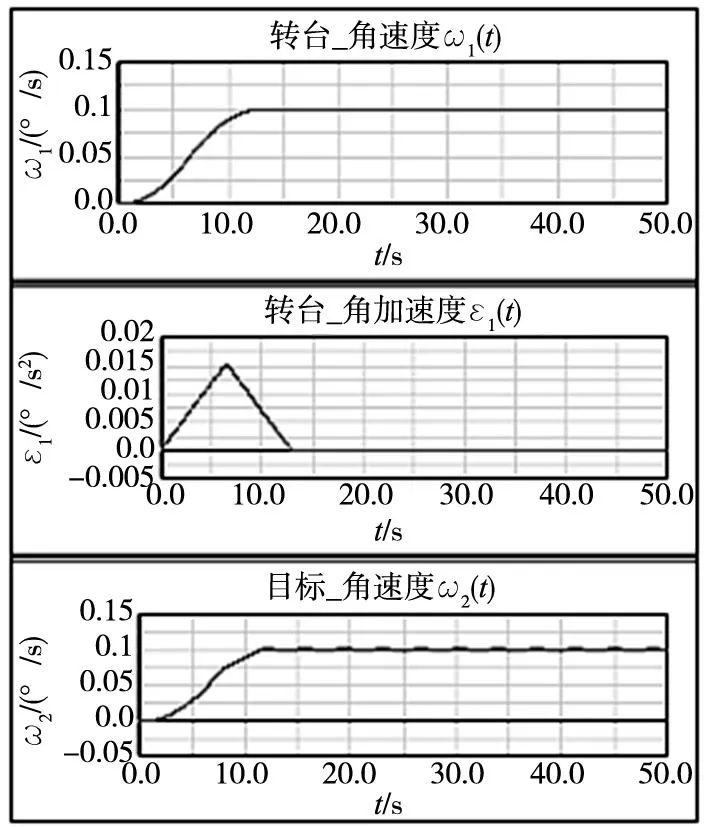
图4　分段S形曲线速度控制的系统启动过程

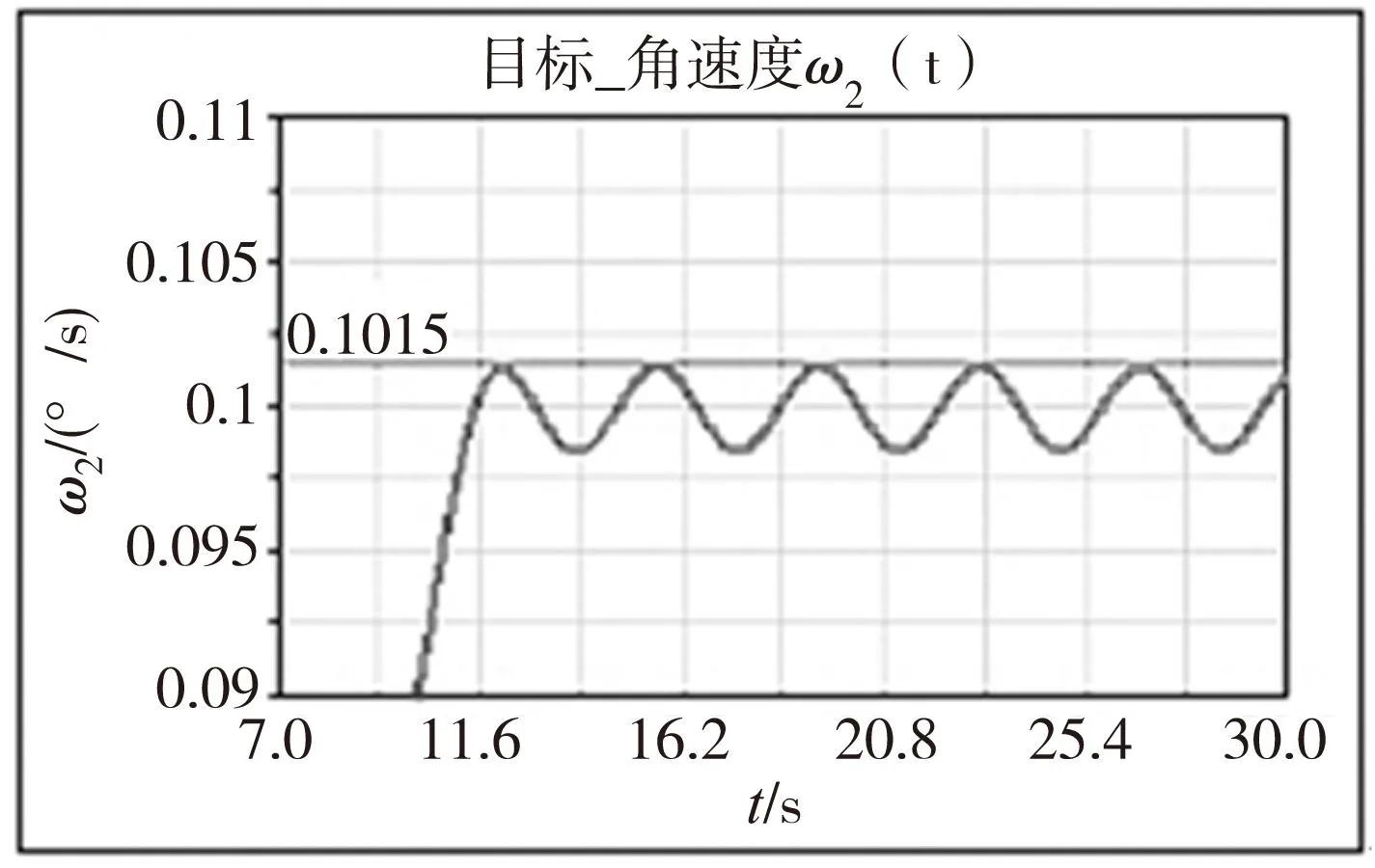
图5　分段S形曲线速度控制的目标角速度曲线特写

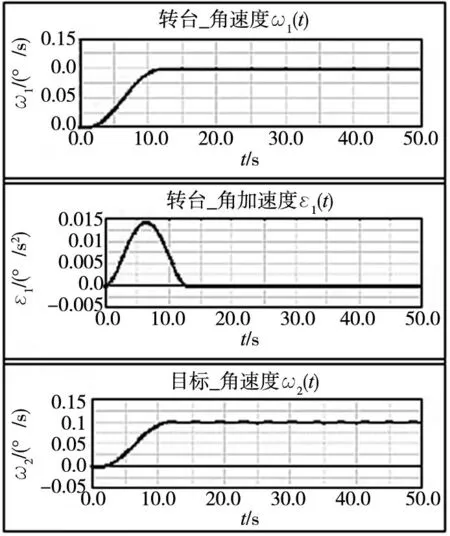
图6　五次多项式速度控制的系统启动过程

图7　五次多项式速度控制的目标角速度曲线特写

3结束语

为满足大惯量弱刚性回转系统平稳启动的要求，本文提出基于五次多项式插值的启动速度控制算法，并推导出基于该算法的数控系统加减速控制模型。通过ADAMS刚柔耦合动力学仿真，验证了该算法对于提高系统柔性的有效性。与传统S形曲线等速度控制算法相比，五次多项式速度控制算法不仅分段简单易于程序实现，而且保证了系统在整个加减速过程中加加速度的连续变化，可有效减小系统加减速过程的冲击和振动，特别适用于传动链刚性较差而对末端执行件速度平稳性要求较高的系统。

[参考文献]

[1] 胡建华,廖文和,周儒荣.CNC系统中几种升降速控制曲线的研究与比较[J].南京航空航天大学学报,1999,31(6):706-711.

[2] 陈友东,王田苗,魏洪兴,等.数控系统的直线和S形加减速研究[J].中国机械工程,2006,17(8):1600-1603.

[3] 石川,赵彤,叶佩青,等.数控系统S曲线加减速规划研究[J].中国机械工程,2007,18(12):1421-1425.

[4] 李晓辉,邬义杰,冷洪滨.S 曲线加减速控制新方法的研究[J].组合机床与自动化加工技术,2007(10):50-53.

[5] 潘海鸿,杨微,陈琳,等.全程S曲线加减速控制的自适应分段NURBS曲线插补算法[J].中国机械工程,2010,21(2):190-196.

[6] 于金刚,林浒,张晓辉,等.一种新型的Jerk连续加减速控制方法研究[J].组合机床与自动化加工技术,2009(8):61-64.

[7] 史步海,郭协涛.基于EMC2的S形加减速控制算法[J].组合机床与自动化加工技术,2013(6):30-33,36.

[8] 冷洪滨,邬义杰,潘晓弘.三次多项式型段内加减速控制新方法[J].浙江大学学报:工学版,2008,42(8):1440-1446.

[9] 郭新贵,李从心.一种新型柔性加减速算法[J].上海交通大学学报,2003,37(2):205-207.

[10]朱春霞,朱立达,刘永贤,等.基于ADAMS的并联机床刚柔耦合系统的协同建模研究[J].组合机床与自动化加工技术,2007(11):1-4.

[11]周成,邵跃林.基于ADAMS与ABAQUS的刚柔耦合动力学分析方法[J].机械制造与自动化,2014,43(1):131-133.

[12]张炜,祝勇仁.基于ANSYS和ADMAS的采煤机钻削机构动力学分析[J].煤矿机械,2014,35(10):114-115.

(编辑赵蓉)

Starting Velocity Control of a Rotary System with Large Inertia and Low Stiffness Based on Quintic Polynomial Interpolation

CHEN Ai-bo, CHEN Wu-yi

(School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)

Abstract：A rotary support system to support large targets for electromagnetic test, has the characteristics of large inertia and low stiffness. To ensure the speed overshoot of the tested target not greater than 0.001°/s caused by the start acceleration from static state to rated speed of 0.1°/s, a speed control algorithm based on single quintic polynomial interpolation along the entire acceleration process is put forward, which not only keeps the speed and acceleration continuous as well as differentiable during the whole process but also guarantees the jerk always changes continuously. Compared with S-shaped acceleration and deceleration control algorithm, the proposed algorithm is much simpler and makes the system more flexible.Rigid-flexible coupling dynamics simulation on the rotary support system processed in ADAMS demonstrates the advantage of the proposed method.

Key words：quintic polynomial; large inertia & low stiffness; speed control

中图分类号：TH166;TG506

文献标识码：A

作者简介：陈爱波(1990—)，男，山东泰安人，北京航空航天大学硕士研究生，研究方向为机械结构优化设计及CAD/CAE技术， (E-mail) sdchenaibo@163.com。

收稿日期：2015-03-15；修回日期：2015-04-15

文章编号：1001-2265(2016)02-0105-03

DOI:10.13462/j.cnki.mmtamt.2016.02.030