五轴数控机床定位误差对刀具轨迹的影响研究*

吴　锐，刘华明，胡泽启

(武汉理工大学 a.汽车工程学院；b.现代汽车零部件技术湖北省重点实验室，武汉　430070)



五轴数控机床定位误差对刀具轨迹的影响研究*

吴锐a，b，刘华明a，b，胡泽启a，b

(武汉理工大学 a.汽车工程学院；b.现代汽车零部件技术湖北省重点实验室，武汉430070)

摘要：针对五轴数控机床的各轴定位误差进行分析，提出了一种包含各轴定位误差的数学模型建立方法。根据此数学模型分析了定位误差对刀具与工件相对运动轨迹的影响关系，并在MATLAB软件平台上分别模拟计算了刀具沿曲线与曲面运动的轨迹，得到了刀具理想轨迹与实际轨迹的相对关系以及各轴定位误差对刀具轨迹的综合影响规律。计算结果表明，此数学模型可以作为分析机床各轴定位精度的理论依据。根据模型计算得到了各轴定位误差对刀具运动轨迹上不同位置点的影响规律，可以为经济型五轴机床的各轴定位精度分析及其补偿提供参考。

关键词：五轴数控机床；定位误差；轨迹模拟

0引言

五轴联动数控机床主要用来加工含复杂曲面的零件，一般是在传统三轴机床的基础上，添加两个方向的旋转运动，使刀具与工件能够实现空间复杂的相对运动，从而达到复杂曲面加工的目的。目前，最常见的两种五轴机床[1]，一是传统三轴外加双摆头的五轴机床，这种机床坐标转换关系简单，加工范围大，但是整体刚度较低；二是传统三轴外加回转工作台的五轴机床，这种机床整体刚度较大，适合加工一些中小型零件。

五轴联动数控机床各轴的精度直接影响着复杂曲面的加工及最终加工质量。目前，国内外对于五轴联动数控机床的精度研究已经取得了一定的成果，其中包括针对几何误差与热误差等静态误差的研究[2]，误差模型的建立和分析[3-5]，定位精度的测量与补偿等[6-7]。对五轴联动数控机床的精度研究中一般为使用激光干涉仪和RX10回转基准分度器来进行几何精度的检测，使用精密线纹尺和光电显微镜来进行重复定位精度的检测[8]，使用双球杆仪来进行运动精度的检测[9-10]。而对于采用行程挡块来控制各轴行程距离的经济型五轴机床来说，使用千分表同样可以满足其精度检测的要求[11]。

在五轴机床的实际工作过程中，每个轴的运动都存在一定的定位误差，对加工精度影响较大。如果各轴定位误差过大，将影响到刀具与工件的相对运动，刀具与工件将不能按照程序预设的轨迹进行运动，从而影响了最终工件的加工质量，所以有必要对五轴机床的各轴定位误差进行研究。

机床的各轴误差分析的一般过程包括模型建立、数值模拟、实验验证[12]、以及指导实际加工中的误差补偿，达到改善加工质量的目的。建模以及数值模拟部分是整个过程的基础，也为后续的机床调试以及误差的补偿提供理论依据，是研究的重点。

1建立五轴机床误差模型

1.1建立误差变换矩阵

包含回转工作台的五轴联动数控机床结构简图如图1所示。其中，主轴可以沿X、Z轴做直线运动，A/C回转工作台可以带动固定在上面的工件一起沿Y轴做直线运动以及分别绕X、Z轴做旋转运动，是一种传统三轴外加回转工作台的五轴数控机床。

根据这种五轴数控机床的结构特征，建立了与机床各轴定位精度相关的误差模型，其中包含了各轴的定位误差，如图2所示。其中机床坐标系为OXYZ，定义坐标系原点为各轴回零后A轴轴线与C轴轴线的交点，坐标轴方向与机床各轴运动方向一致。在机床坐标系上，以坐标系原点的移动以及坐标轴的旋转来表示各轴的定位误差，直线轴的误差相当于坐标系原点O偏移至O1，A轴、C轴的误差相当于X1轴、Z1轴的旋转，则形成新的坐标系O1X1Y1Z1。误差模型中包含了机床五轴的定位误差，其中，ΔX、ΔY、ΔZ分别代表X轴、Y轴、Z轴的定位误差，Δφ代表A轴定位误差，Δθ代表C轴定位误差。

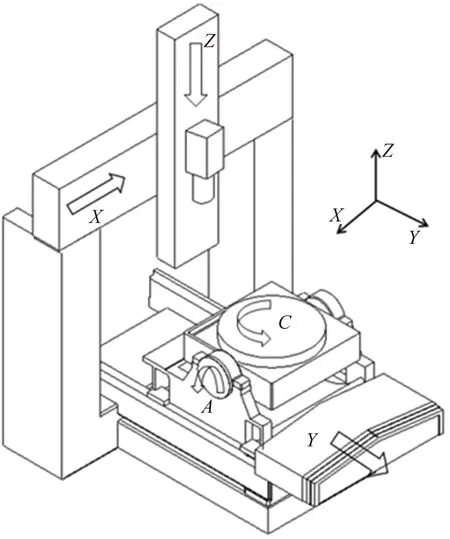
图1　带回转工作台的五轴数控机床简图

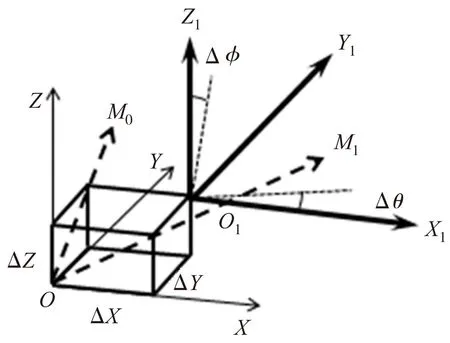
图2　五轴数控机床各轴定位误差模型

在上述误差模型的基础上，利用齐次变换矩阵的方法，建立包含五轴机床各轴定位误差的数学模型。如图2所示，设定工件上的某一空间点为M0，为了简化直线方向上误差的变换矩阵表达式，使用加1的齐次坐标来表示空间向量[13]。(X0,Y0,Z0,1)T为向量OM0的齐次坐标，其中的X0、Y0、Z0确定了空间点M0在机床坐标系OXYZ中的位置。根据上述误差模型，可以通过数学关系得到含各项误差的变换矩阵表达式，即公式(1)～(3)。

包含A轴定位误差的变换矩阵表达式为：

(1)

包含C轴定位误差的变换矩阵表达式为：

(2)

包含X、Y、Z轴定位误差的变换矩阵表达式为：

(3)

上述三个矩阵中：RA表示单独考虑A轴定位误差的变换矩阵，左乘RA即表示A轴旋转Δφ；RC表示单独考虑C轴定位误差的变换矩阵，左乘RC即表示C轴旋转Δθ；SXYZ代表考虑X轴、Y轴、Z轴定位误差的变换矩阵，左乘SXYZ即表示X轴、Y轴、Z轴分别平移ΔX、ΔY、ΔZ。

1.2空间点的位置分析

由于上述五轴定位误差的存在，使得在实际零件加工过程中，刀具与被加工工件相对轨迹产生了偏差。为了计算这种偏差的大小，首先考虑工件上某一空间点的位置变化。机床实际运行中，五项定位误差使理想空间点M0的位置变成了实际点M1。向量OM1的齐次坐标为(X1,Y1,Z1,1)T，其中的X1、Y1、Z1确定了点M1在机床坐标系OXYZ中的位置，并有公式：

(4)

公式(4)中利用了上述各轴误差的变换矩阵，将理想空间点M0转换为实际点M1。公式(1)～(3)的各轴误差变换矩阵带入公式(4)并展开求解，即可得到实际点M1的坐标为：

(5)

理想点M0与实际点M1之间的距离为ΔL，并有：

(6)

公式(5)、(6)中包含了五轴机床的5项定位误差值(ΔX、ΔY、ΔZ、Δφ、Δθ)。公式(5)给出了在各轴定位误差的影响下，五轴机床中空间理想位置点M0与实际位置点M1之间的位置关系。通过公式(6)可以计算出理论位置点相对于实际位置点所偏移的距离。

2刀具运动轨迹分析

在五轴数控机床的实际工作过程中，刀具相对与工件往往是沿曲线轨迹运动，所以在各轴定位误差存在的情况下，对刀具曲线和曲面轨迹分别进行了模拟计算。根据公式(5)、(6)可以模拟计算出任意空间轨迹的实际位置以及理想轨迹上各点的偏移距离。

取任意一条空间曲线，其轨迹方程为：

(7)

由于五轴机床各轴定位误差的影响，实际空间曲线轨迹方程变为：

(8)

实际曲线轨迹上每个点(x1,y1,z1)与理想轨迹上对应点(x,y,z)之间的关系由公式(5)给出。

在MATLAB软件中模拟计算某一特定曲线轨迹的变化，如图3所示。假定刀具按照特定的空间曲线轨迹①运动，考虑各轴定位误差之后，将选定的5项定位误差代入上述公式(5)、(8)，绘制得到曲线②，即考虑各轴定位误差之后的实际轨迹。所给定的误差为国标中规定的五轴机床各轴最大定位误差[14]，数据如表1所示。

表1　各轴给定误差值

求解得到曲线理想轨迹与实际轨迹在每个对应位置点之间的偏差大小，如图4所示。分析时，将理想轨迹曲线①离散为2000个点，其中X轴代表这些离散点的序号，Y轴代表每个点与它所对应实际点的偏差值。可以发现在所取的特定曲线轨迹中，第500个点的位置处，误差引起的轨迹偏差值最小，第1500个点的位置处，误差引起的轨迹偏差值达到最大。

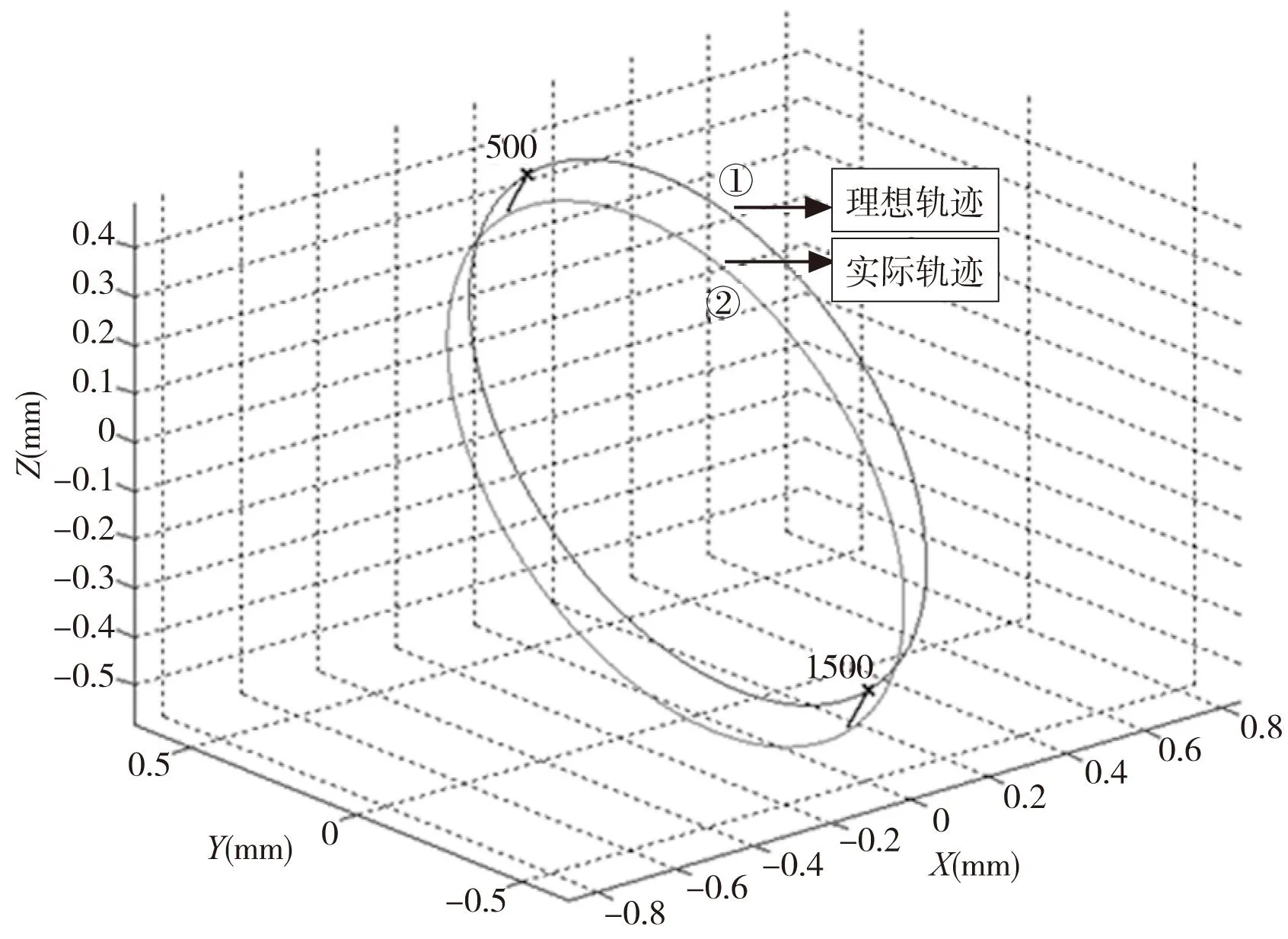
图3　曲线轨迹图

图4　曲线轨迹偏差图

然后按照同样的方法，分析定位误差对曲面轨迹的影响。在加工含特殊曲面的工件时，刀具与工件的相对轨迹可以看作是多条曲线轨迹的叠加。

取任意的一个空间曲面轨迹方程为：

R(x,y,z)=0

(9)

由于五轴机床各轴定位误差的影响，实际空间曲面的轨迹方程变为：

R(x1,y1,z1)=0

(10)

同曲线轨迹的计算一样，曲面上每个实际位置点(x1,y1,z1)与理想位置点(x,y,z)的关系由公式(5)给出。

按照同样的方法，在MATLAB中模拟计算某一特定曲面轨迹的变化，如图5所示。其中的曲面①为刀具运动的理想轨迹，将上表1中给定的 5项定位误差值代入上述公式(5)、(10)后，绘制得到考虑各轴定位误差之后的实际轨迹，即曲面②。

求解得到曲面理想轨迹与实际轨迹在每个对应位置点之间的偏差大小，如图6所示。可以发现在所取的特定曲面轨迹中，坐标点(0，4，1.2)处误差引起的轨迹偏差值最小，坐标点(4，0，0.64)处误差引起的轨迹偏差值达到最大。

图5　曲面轨迹图

图6　曲面轨迹偏差图

从上述的刀具理想轨迹与带误差的实际轨迹分析中可以看出，由于五轴机床各轴定位误差的影响，刀具实际运动轨迹在不同位置发生了不同程度的偏移，并且发生偏移的位置以及偏移的程度可以利用MATLAB软件进行模拟计算得到。上述的偏差结果以及变化趋势与公式(6)的理论计算部分结果一致。

3结论

(1)建立了与五轴机床各轴定位误差相关的误差模型，并通过齐次变换矩阵的方法得到了含误差的数学模型，推导了包含各轴定位误差的曲线以及曲面加工轨迹方程，最后得到了理论点与对应的实际点之间距离的计算公式。

(2)根据数学模型在MATLAB中模拟计算了刀具沿曲线以及曲面轨迹的变化，得到了刀具理想轨迹与实际轨迹的位置关系。刀具曲线和曲面轨迹中，不同位置点发生了不同程度的偏移，偏移的距离可以通过软件计算得到。模拟计算的结果可以指导五轴数控机床后续的调试工作，对五轴数控机床定位误差的补偿研究有重要意义。

[参考文献]

[1] 梁铖，刘建群.五轴联动数控机床技术现状与发展趋势[J].机械制造，2010，48(1)：5-7.

[2] W T Lei, Y Y Hsu. Accuracy test of five-axis CNC machine tool with 3D probeball.Part1:design and modeling[J].Machine Tools and Manufacture,2002(42):1153-1162.

[3] Masaomi Tsutsumi, Akinori Saito. Identification of angular and positional deviations inherent to 5-axis machining centers with a tilting-rotary table by simultaneous four-axis control movements[J].Machine tools and Manufacture, 2004(44):1333-1342.

[4] 包丽，张洪军.五轴加工中心空间误差分析及补偿研究[J].机械设计与制造，2014 (7)：127-129.

[5] 黄克，关立文，王立平.五轴数控机床精度建模与预测研究[J].组合机床与自动化加工技术，2015(2)：78-81.

[6] 高秀峰，刘春时.A/C轴双轴转台几何误差检测与补偿技术研究[J].机械传动，2012，36(3)：10-13.

[7] 唐进元，龙云泽.数控弧齿锥齿轮磨齿机回转轴定位误差检测及补偿研究[J].机械传动，2010，34(6)：5-11.

[8] 冷汹涛.数控机床定位精度和重复定位精度的检验[J].机床与液压，2008，36(8)：191-192.

[9] 柳耀阳，刘春时，李焱.双轴转台精度检测与研究[J].机械设计与制造，2012(1)：136-138.

[10] 王民，胡建忠，昝涛.五轴数控机床运动误差建模与测试技术[J].北京工业大学学报，2011，36(4)：433-439.

[11] 余仲裕.数控机床维修[M].北京：机械工业出版社，2007.

[12] 韩飞飞，赵继，张雷.数控机床几何精度综合解析与试验研究[J].机械工程学报，2012，48(21)：141-148.

[13] 郑剑锋.多轴数控机床误差测量与建模研究[C].北京:北京交通大学,2014.

[14] GB/T 18400.4-2010，加工中心检测条件，第4部分：线性和回转轴线的定位精度和重复定位精度检验[S].

(编辑赵蓉)

Influence of Positioning Error on Tool Trajectory in Five-axis CNC Machine Tools

WU Ruia,b，LIU Hua-minga,b，HU Ze-qia,b

(a.School of Automotive Engineering;b.Hubei Key Laboratory of Advanced Technology for Automotive Components, Wuhan University of Technology,Wuhan 430070,China)

Abstract：The positioning accuracy of each axis of five-axis CNC machine tool were analyzed, and the method of establishing mathematical model contained the positioning error of each axis was proposed. Then the influence of positioning error on the relative motion trajectory between the tool and the part was obtained, according to the mathematical model. And the MATLAB was used to simulate the tool trajectory along curve and curved surface, the relationship between the ideal trajectory and actual trajectory of tool and the combined effects of positioning error of each axis on the tool trajectory was obtained. The calculation results show that the mathematical model can be used as theoretical basis for analysis of positioning accuracy. According to the model calculation, the influence of each axis positioning error in the different point of the tool trajectory was got, which can provide a reference for the study of precision and compensation of economical five-axis machine tools.

Key words：five-axis CNC machine tools; positioning error; trajectory simulation

中图分类号：TH161；TG659

文献标识码：A

作者简介：吴锐(1990—)，男，湖北黄冈人，武汉理工大学硕士研究生，研究方向为自动化加工设备，(E-mail)whutwurui@163.com。

*基金项目：湖北省重大科技成果转化与产业化项目(2012AAA07-01)；湖北省科技支撑计划项目(2012BAA08001)

收稿日期：2015-09-14

文章编号：1001-2265(2016)02-0098-04

DOI:10.13462/j.cnki.mmtamt.2016.02.028