初始投标值数量和样本容量对双边界二分式CVM的影响
2016-04-13敖长林王世雪
敖长林, 周 领, 焦 扬, 王世雪
东北农业大学, 管理科学与工程系, 哈尔滨 150030
初始投标值数量和样本容量对双边界二分式CVM的影响
敖长林*, 周领, 焦扬, 王世雪
东北农业大学, 管理科学与工程系, 哈尔滨150030
摘要:双边界二分式条件价值评估法是当前广泛应用于评估生态环境和自然资源价值的陈述偏好法。为了研究双边界二分式CVM中,不同分布中初始投标值数量及样本容量对WTP的影响,应用蒙特卡洛模拟和支付意愿函数模型相结合的方法,用概率分位数设计投标值,分别选择数据来源不同的Weibull分布和对数Logistic分布,动态模拟不同初始投标值数量和样本容量对WTP期望值产生的影响。模拟结果表明,对不同的WTP概率分布,初始投标值数量和样本容量对WTP的影响趋势是一致的,当初始投标值数量和样本容量分别大于5和500时,初始投标值数量和样本容量的增加,对WTP估计值的影响程度越来越小。研究结果表明,在二分式CVM研究中,当以WTP期望为代表值时,其初始投标值数量和样本容量至少为5和500。研究结论为二分式CVM问卷设计中投标值数量及样本容量的设定提供参考依据。
关键词:双边界二分式; 支付意愿; 蒙特卡洛模拟; 初始投标值数量; 样本容量
条件价值评估法(CVM)是一种典型的陈述偏好评估法,被广泛应用于生态资源环境的非使用价值评估中[1]。CVM是在假想的市场条件下,通过直接向受访者调查和询问他们对某一生态资源环境改善和保护措施的支付意愿(WTP),或对某一生态资源环境的破坏和损失所愿意接受的补偿意愿(WTA),最终用受访者的WTP或WTA来估计某一生态资源环境的经济价值[2]。
1963年美国哈佛大学R.Davis[3]首次将CVM应用于缅因州林地的娱乐价值的评估。1984年,美国加州大学的Hanemann[4]将CVM与随机效用最大化理论(RUM)相结合,为CVM奠定了重要的经济学基础。1976年,Bishop[5]和Heberlein将封闭式问题结构引入到CV中,提出了二分式条件价值评估(DCCV)。此后,Hanemann和Cameron[6]等对DCCV这一理论进行了深化发展,使其得到了更广泛的应用[7]。1986年,Carson[8]等人在DCCV的基础上提出了双边界二分式(DBDC)条件价值评估法。Hanemann等人证明DBDC能够收集更多的关于受访者WTP的信息,同时也比以往的单边界二分式(SBDC)更具有效率和科学性[9]。DBDC-CVM能够有效地模拟市场交易行为,精确地描述假想市场,避免假想偏差,更加真实的反映了受访者的WTP或WTA[10],因此在国外各个领域得到了广泛的研究和应用[11- 14]。与国外相比,CVM在我国的研究还处于起步阶段,问卷设计还是以早期的支付卡为主,DBDC-CVM理论研究及其应用案例相对较少。
CVM研究一般分为3个步骤:问卷设计、问卷发放回收及数据分析[15]。问卷设计和发放是关系到CVM研究成败的关键环节,问卷初始投标值数量和样本容量会影响CVM的评估结果。目前CV问卷设计中初始投标值数量是通过预调研来确定。1991年Duffield和Patterson[16]在前人的基础上提出投标值设计及其样本容量分配的方法,Cooper[17]在此基础上进一步提出投标值及样本在各投标值分配的最优设计方法。1993年,Kanninen[18]研究了DBDC-CVM中投标值对WTP的影响,得出最优投标值设计。Boyle[19]和Roach[20]分别从单边界和多边界角度讨论了CV中投标值的设计。以上研究大多局限在讨论投标值或其所分配的样本数量对WTP产生的影响,而缺少初始投标值数量和样本容量的组合对WTP影响的研究,缺少确定选择初始投标值数量和样本容量的定量依据。过多的初始投标值数量和样本容量会增加问卷的设计难度,提高调研成本,而过少的数量又会影响收集数据及评估结果。
本文在已有研究的基础上[21- 25],应用支付意愿函数模型,通过蒙特卡洛模拟,分别选择数据来源不同的Weibull分布和对数Logistic分布,探讨不同的初始投标值数量和样本容量对WTP的动态影响,依据WTP均方误差(MSE)变化趋势得到初始投标值数量和样本容量的最低数量。和目前DBDC-CVM研究现状相比[17- 20],本文的贡献是从初始投标值数量和样本容量这两个角度,讨论两者的组合对WTP期望值的动态影响,并给出初始投标值和样本容量的最低数量,研究结果为CVM问卷中初始投标值数量及样本容量的确定提供定量参考依据。
论文共分三部分:第一部分介绍CVM计算模型中的支付意愿函数模型;第二部分,应用蒙特卡洛模拟,讨论Weibull分布和对数Logistic分布中不同初始投标值数量和样本容量对WTP期望值的影响;第三部分为结论和讨论。
1DBDC-CVM计算模型
蒙特卡洛模拟中的核心是通过计算WTP的均方误差讨论初始投标值数量及样本容量对WTP的影响。在计算WTP时,运用Cameron[26]提出的支付意愿函数模型,通过受访者的支付意愿和提示额的关系,估计受访者的支付意愿。
DBDC-CVM是在SBDC的基础上通过受访者对封闭式投标值给出4种回答:同意/同意,同意/不同意,不同意/同意,不同意/不同意,根据受访者反映结果的概率和投标值之间的函数关系,来推导出受访者的WTP或WTA[27]。
受访者的WTP值为非负的随机变量,假设WTP的表达式为:
logWTPi=μ+εi
(1)
式中,WTPi表示的是受访者i的真实WTP值;μ是一个未知的参数;εi为误差项,服从平均值为0,标准差为σ的概率分布。

(2)
(3)
(4)
(5)
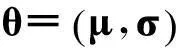
(6)
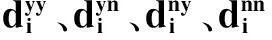
根据参数估计值可以推导出WTP的生存函数,进而可以计算出WTP的期望和中位数。WTP的生存函数为:

(7)
WTP期望值的计算公式为[28]:
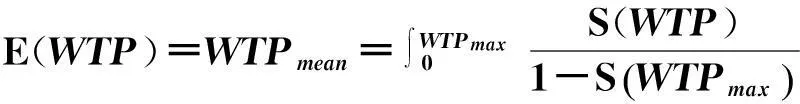
(8)

而对于WTP中位数的计算,就是求解表达式S(WTP)=0.5。对于假定的分布为正态分布或者Logit分布,则WTP中位数为:
WTPmedian=exp(μ)
(9)
如果假定的WTP为Weibull分布,则WTP中位数的表达式为:
(10)
2初始投标值数量和样本容量的蒙特卡洛模拟
蒙特卡洛模拟是一种随机模拟方法。其核心思想是通过所求的问题建立概率模型,使它的参数等于所求问题的解;再通过对模型重复抽样试验,计算所求参数[29],从而得到所求问题的近似解。本文应用不同的WTP分布概率模型,通过蒙特卡洛模拟探讨初始投标值数量和样本容量对WTP的影响。
2.1数据来源
Weibull分布和对数Logistic分布在二分式CVM研究中得到广泛应用,在二分式CVM的概率模型中具有一定的代表性。因此选择这两个不同的概率模型进行蒙特卡洛模拟。
Weibull分布的数据来源于三江平原湿地问卷调查数据。2011年6月至10月期间共发放纸质问卷1302份、网上问卷665份,分别回收1003份以及194份,回收率为77.0%、29.2%,得到有效问卷927份,其中抗议问卷(即零支付问卷)326份,调查问卷的正支付率为64.8%。问卷有7个初始投标值,分别为1, 5,10,20, 50,100,200。
对数Logistic分布的数据来源于Jun Zhao等人对上海张家浜河生态系统的价值评价和恢复的研究结果[30],共发放了640份问卷,收回507份有效问卷,问卷中有9个投标值,分别是5,10,25,50,100,150,200,300,500。
2.2概率模型的建立
概率模型即为WTP的分布函数,模拟所产生的随机数序列及计算WTP所需的数据都是由这个分布函数所产生。
Weibull模型在双边界二分式CVM计算模型中已得到广泛应用。根据调研得到的DBDC-CVM数据,通过统计分析,得到WTP服从Weibull分布的概率密度函数为:
(11)
式中,WTP的期望值是165.654(元),中位数是173.457(元)。
对数Logistic分布也是在CVM研究中常用的分布,根据Jun Zhao等人研究结果,WTP服从对数Logistic分布的概率密度函数为:
(12)
式中,WTP的期望值是157.033 元,中位数是74.965 元。
2.3蒙特卡洛模拟步骤
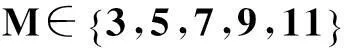
(2) 投标值的设定:由WTP的分布模型,随机产生N个真实WTP值(TWTP),将每个TWTP值转换成DBDC-CVM数据,根据所获得的数据计算模拟WTP值(SWTP)。对于双边界的投标值,若有M个初始投标值,则有相对应的M个支付方案。设定第k个初始投标值为Bk(k=1,2,3,…,M),双边界中较高的投标值为Bku,较低的投标值为Bkd,同时设定Bku=Bk+1和Bkd=Bk-1。除了M个初始投标值外,还有两个特殊的投标值,分别是第一种支付方案中比最小的初始投标值还小的投标值和最后一种支付方案中比最大的初始投标值还大的投标值。因此在模拟试验中共有M+2个不同的投标值,这M+2个投标值由WTP服从的分布函数的M+3分位数计算得到[33]。
(3)系统模拟次数为1000次,取平均数作为最后的SWTP值。
(4)根据计算得到的SWTP与WTP的分布函数,分别计算WTP期望值的偏差,标准差和MSE。
2.4模拟结果
根据所建立的概率模型式(11)和式(12),利用S-PLUS统计软件[34], 分别对Weibull分布和对数Logistic分布的WTP期望值进行蒙特卡洛模拟。
2.4.1Weibull分布的WTP期望值的模拟结果
对于WTP期望值的蒙特卡洛模拟结果如表1所示,其中:M是初始投标值数量,N是样本容量,S.D.是标准差,Bias是偏差。其模拟结果MSE的三维图如图1所示,其中水平轴分别为初始投标值数量和样本容量,垂直轴为WTP期望值的MSE。从3个不同的角度观察分别得到等高线图2、初始投标值数量与MSE的关系图3及样本容量与MSE的关系图4。

表1 Weibull分布的WTP期望值的标准差、偏差、均方误差
S.D.:标准差Standard deviation, MSE:均方误差Mean squared error
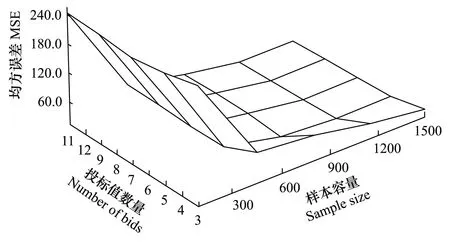
图1 均方误差三维图Fig.1 3D graph of MSE, sample size, number of bids
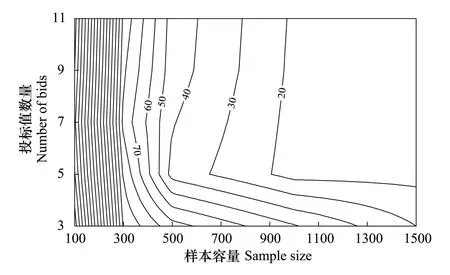
图2 均方误差等高线图Fig.2 Map of contour line
由等高线图2可见,样本容量从100到300的区间内,等高线是垂直的,同时分布密集。说明当样本容量在100和300之间,无论初始投标值数量如何变化,MSE都是稳定不变的,即初始投标值数量的增减变得毫无意义。当样本容量不断增加时,MSE急剧的减小。由图3,当样本容量为100和300时,初始投标值数量不断增加时,MSE的大小没有太大的变化。由图4,对于任何初始投标值数量,当样本容量不断增加时,MSE在不断减少,而当样本容量在100到300之间时,MSE的降幅最大。
由等高线图2,当样本容量超过300时,初始投标值数量以5为分界线,当初始投标值数量在5上下变动时,MSE明显有不同的变化。当初始投标值数量在5以下时,初始投标值数量的增加对MSE的影响效果比样本容量的增加更明显。由图3可见,当样本容量为500,1000和1500时,初始投标值数量从3增加到5,MSE减少的幅度较大。由图4,当初始投标值数量大于5时,其对MSE的影响基本相同。初始投标值数量的增加变得没有意义,样本容量的增加对MSE的影响效果要更明显。

图3 投标值数量对均方误差的影响Fig.3 The influence of number of initial bids to MSE
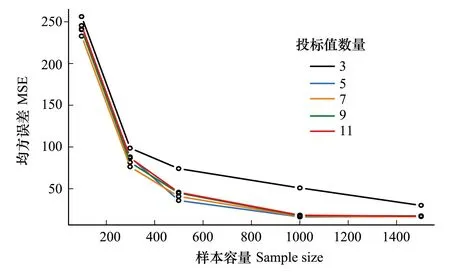
图4 样本容量对均方误差的影响Fig.4 The influence of sample size to MSE
综上,对Weibull分布而言,当初始投标值数量为5以上,样本容量为大于500时,MSE变化的方向基本一致,其等高线基本平行,同时MSE的降幅也在缓慢变小。
2.4.2对数Logistic分布的WTP期望值的模拟结果
对数Logistic分布的WTP期望值的蒙特卡洛模拟结果如表2所示。其模拟结果MSE的三维图如图5所示,其中水平轴分别为初始投标值数量和样本容量,垂直轴为WTP期望值的MSE。从3个不同的角度观察分别得到等高线图6、初始投标值数量与MSE的关系图7及样本容量与MSE的关系图8。
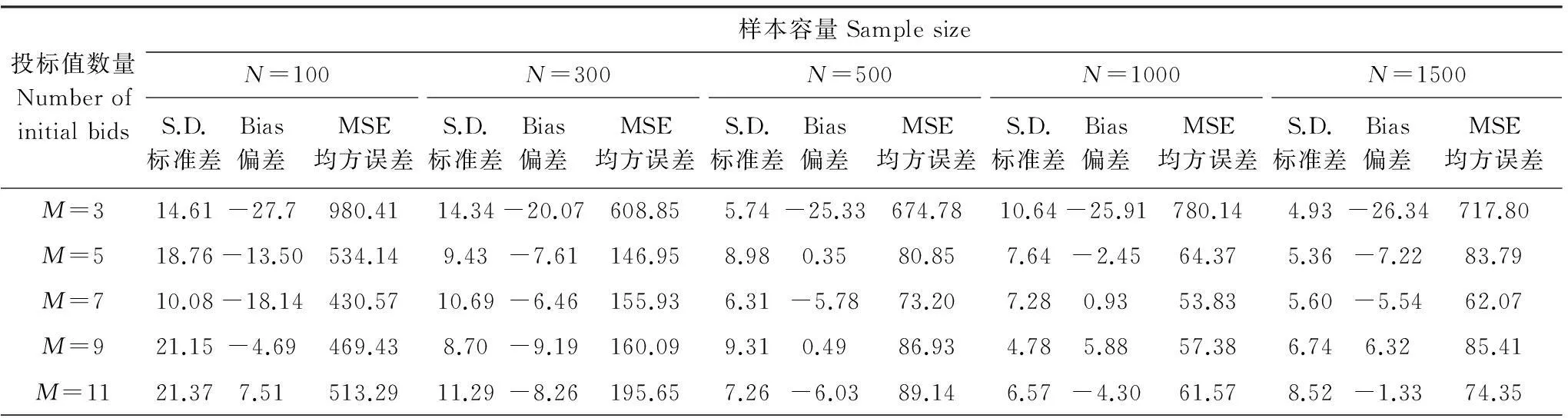
表2 对数Logistic分布的WTP期望值的标准差、偏差、均方误差
S.D.:标准差Standard deviation, MSE:均方误差Mean squared error
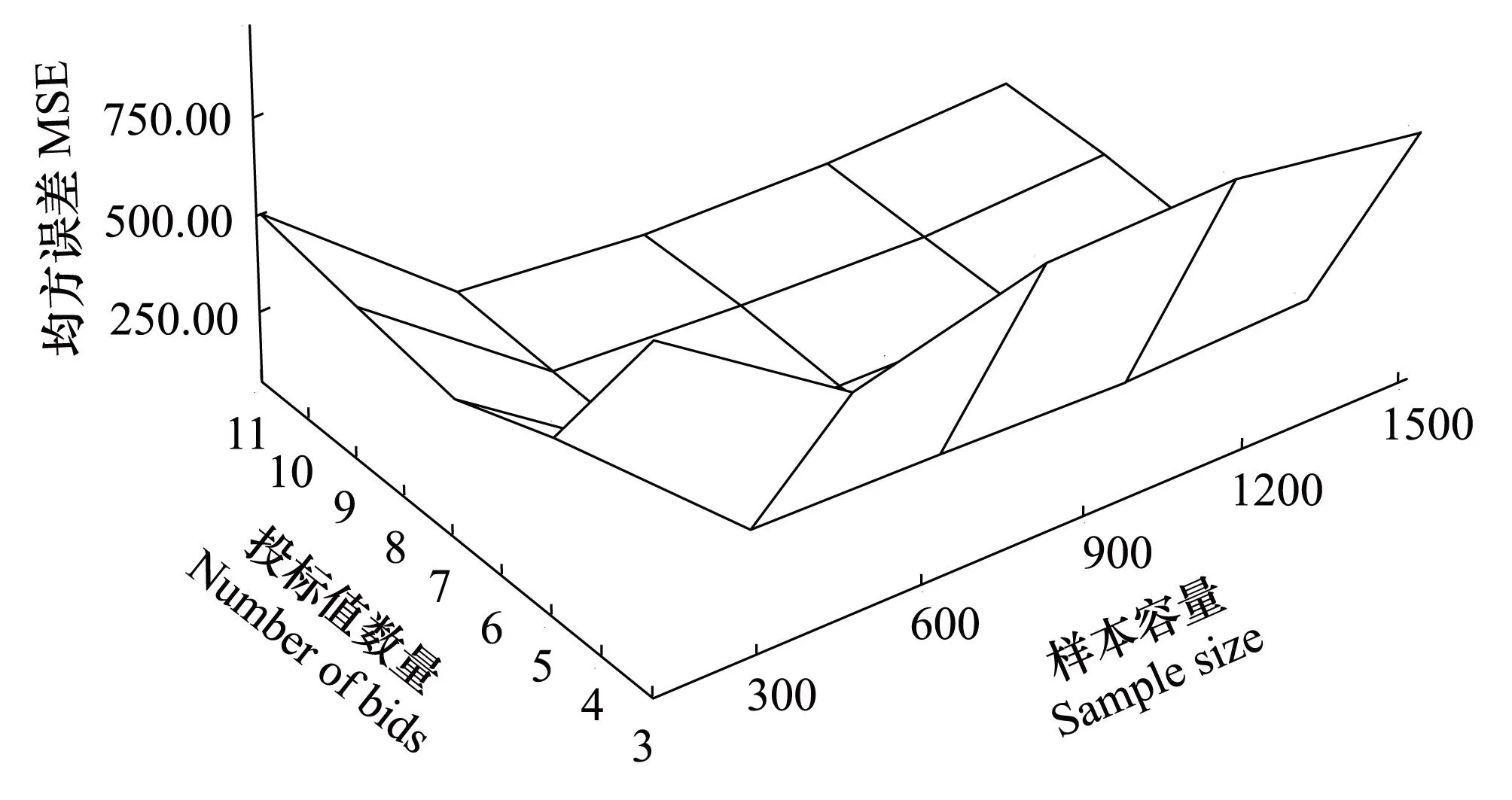
图5 均方误差三维图Fig.5 3D graph of MSE,sample size,number of bids
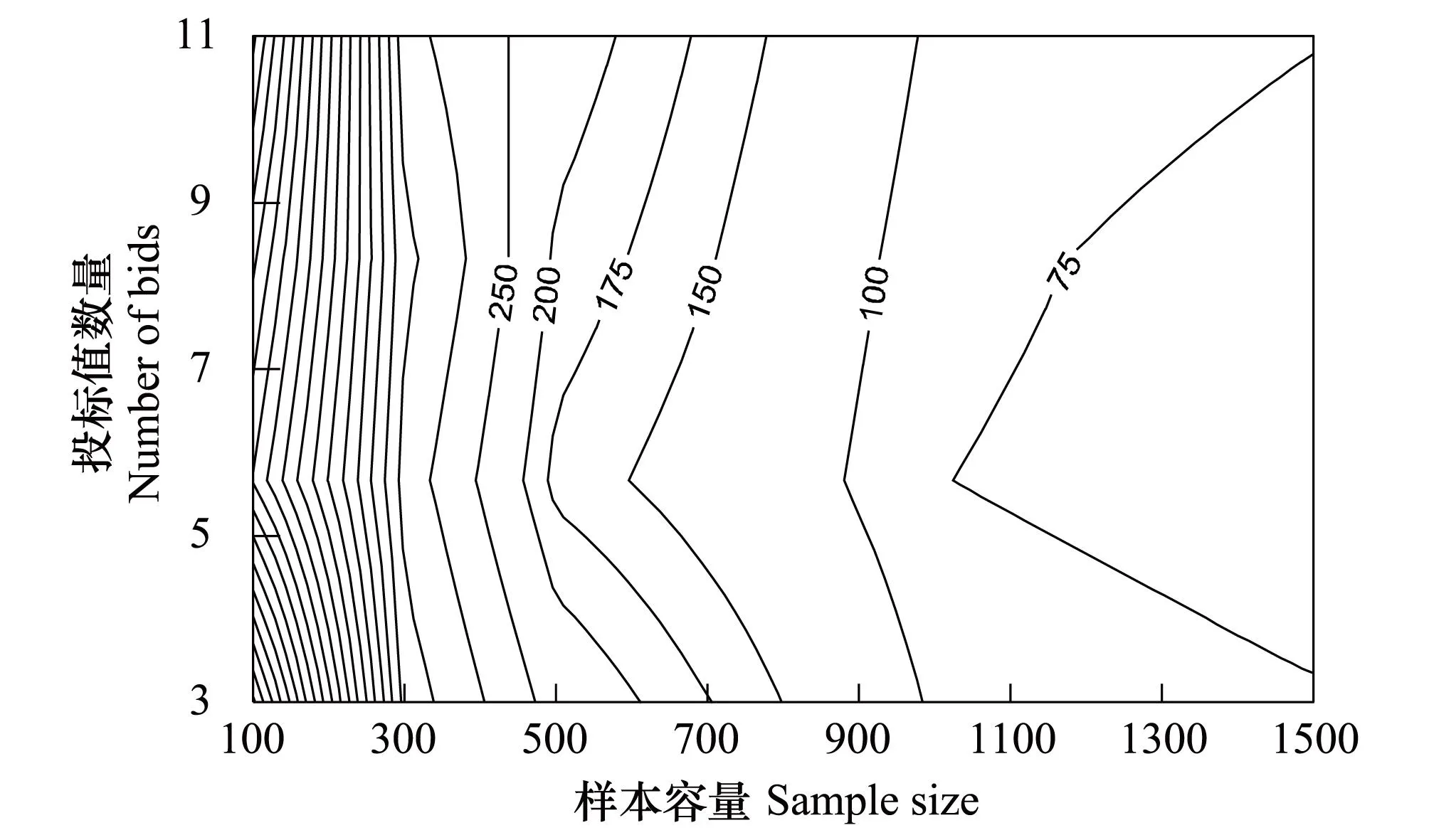
图6 均方误差等高线图Fig.6 Map of contour line
由等高线图6可见,当样本容量在100到300之间,等高线分布密集。由图8,当样本容量在100到300之间时,MSE的降幅最大,大于300时,降幅逐渐减缓。
由等高线图2及图6可见,对数Logistic分布与Weibull分布的等高线图的变化趋势相同。由图7,投标值由3增加到5时,MSE减少的幅度最大。由图8,初始投标值数量为3时,MSE的变化明显高于其他4个投标值对MSE的影响。当初始投标值数量大于5时,MSE变化趋势基本一致。
由等高线图6,当样本容量超过300时,初始投标值数量以5为分界,当初始投标值数量在5上下变动时,MSE明显有不同的变化。当初始投标值数量在5以下时,初始投标值数量的增加对MSE的影响效果比样本容量的增加更明显。当初始投标值数量大于5时,其对MSE的影响基本相同。说明初始投标值数量的增加变得没有意义,而样本容量的增加对MSE的影响效果要更明显。

图7 投标值数量对均方误差的影响Fig.7 The influence of number of initial bids to MSE
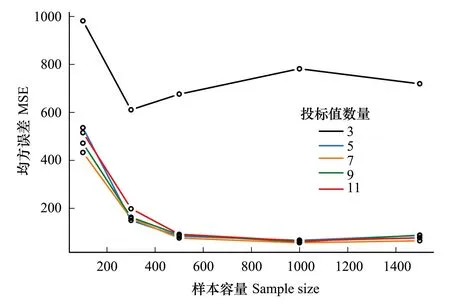
图8 样本容量对均方误差的影响Fig.8 The influence of sample size to MSE
综上,对对数Logistic分布而言,在初始投标值数量为5以上,样本容量大于500时,MSE变化的方向基本一致,其等高线几乎平行,同时MSE的降幅也在缓慢变小,与Weibull模型得出的结果相同。
3讨论
(1)本文的计算模型得出的WTP值,是截断WTP平均值,用最大的投标值对WTP进行右切断,更加符合接近真实的WTP值。而对于包含在问卷中的零支付,论文并没有进行特别处理,如何在模拟的过程中考虑并计算零支付对WTP的影响,将是进一步研究的问题。
(2)本文仅是CVM问卷设计中有关初始投标值数量和样本容量选择问题的探索性研究,仅从MSE的角度考察初始投标值数量和样本容量对WTP期望值的影响,研究的是MSE的大小及变化趋势。选择CVM数据分析中广泛使用的两种分布:Weibull分布和对数Logistic分布,且两种分布的样本数据来源于不同的应用案例,通过蒙特卡洛模拟,探讨初始投标值数量及样本容量对WTP估计值的影响。这两种概率模型虽具有一定的代表性,但仍有局限性。相关研究结论对其他概率模型的普适性问题,还有待进一步研究和探讨。
(3)在蒙特卡洛模拟中,为了模拟计算的方便,用分位数设计投标值,同时假定每个投标值所分配到的样本容量是相等的。如何在模拟试验过程中设计更合理、更符合实际的投标值及每个投标值上样本容量的分配,完善模拟试验,这些都是进一步研究的问题。
4结论
通过蒙特卡洛模拟,以支付意愿函数模型中的Weibull分布和对数Logistic分布为理论模型,应用分位数设计投标值,探讨DBDC-CVM问卷设计中的初始投标值数量和问卷发放中的样本容量对WTP期望值的影响。得出对于Weibull模型和对数Logistic模型,样本容量和初始投标值数量对WTP期望值的影响规律相同。当样本容量大于500,初始投标值数量大于5时,初始投标值数量和样本容量的增加,对WTP的MSE的影响趋势基本一致,且其影响程度逐渐降低。
研究结果表明,从WTP的MSE角度,在 DBDC-CVM的问卷设计中,初始投标值数量至少为5,样本容量至少为500。通过蒙特卡洛模拟,从动态角度讨论初始投标值数量与样本容量的组合对WTP的影响。为CVM问卷设计中投标值数量及样本容量的设定提供参考依据。
参考文献(References):
[1]陈琳, 欧阳志云, 王效科, 苗鸿, 段晓男. 条件价值评估法在非市场价值评估中的应用. 生态学报, 2006, 26(2):610- 619.
[2]张志强, 徐中民, 程国栋, 苏志勇. 黑河流域张掖地区生态系统服务恢复的条件价值评估. 生态学报, 2002, 22(6):885- 893.
[3]Davis R K. Recreation planning as an economic problem. Natural Resources Journal, 1963, 3(2):239- 249.
[4]Hanemann W M. Welfare evaluations in contingent valuation experiments with discrete responses. American Journal of Agricultural Economics, 1984, 66(3):332- 341.
[5]Bishop R C, Thomas H A. Measuring values of extra-market goods:Are indirect measures of value biased? American Journal of Agricultural Economics, 1979, 61(5):926- 930.
[6]Cameron T A. A new paradigm for valuing non-market goods using referendum data:maximum likelihood estimation by censored logistic regression. Journal of Environmental Economics and Management, 1988, 15(3):355- 379.
[7]Díaz M A, Gómez M G, GonzálezS, De Ualvarez J. On dichotomous choice contingent valuation data analysis:Semiparametric methods and Genetic Programming. Journal of Forest Economics, 2010, 16(2):145- 156.
[8]Carson R T, Hanemann W M, Mitchell R C. Determining the Demand for Public Goods by Simulating Referendums at Different Tax Prices. San Diego:Manuscript, University of California, 1986.
[9]Hanemann M, Loomis J, Kanninen B. Statistical efficiency of double-bounded dichotomous choice contingent valuation. American Journal of Agricultural Economics, 1991, 73(4):1255- 1263.
[10]蔡春光, 陈功, 乔晓春, 郑晓瑛. 单边界、双边界二分式条件价值评估方法的比较——以北京市空气污染对健康危害问卷调查为例. 中国环境科学, 2007, 27(1):39- 43.
[11]Barrena J, Nahuelhual L, Báez A, Schiappacasse I, Cerda C. Valuing cultural ecosystem services:Agricultural heritage in Chiloé island, southern Chile. Ecosystem Services, 2014, 7:66- 75.
[12]Jang J Y, Lee J, Yoo S H. The public′ s willingness to pay for securing a reliable natural gas supply in Korea. Energy Policy, 2014, 69:3- 13.
[13]Ikeuchi A, Tsuji K, Yoshikane F, Ikeuchi U. Double-bounded dichotomous choice CVM for public library services in Japan. Procedia-Social and Behavioral Sciences, 2013, 73:205- 208.
[14]Rhee H C. Willingness to pay for avoiding infection of climate change diseases, in particular Tsutsugamushi disease. Osong Public Health and Research Perspectives, 2013, 4(1):16- 20.
[15]Hoehn J P, Randall A. A satisfactory benefit cost indicator from contingent valuation. Journal of Environmental Economics and Management, 1987, 14(3):226- 247.
[16]Duffield J W, Patterson D A. Inference and optimal design for a welfare measure in dichotomous choice contingent valuation. Land Economics, 1991, 67(2):225- 239.
[17]Cooper J C. Optimal bid selection for dichotomous choice contingent valuation surveys. Journal of Environmental Economics and Management, 1993, 24(1):25- 40.
[18]Kanninen B J. Optimal experimental design for double-bounded dichotomous choice contingent valuation. Land Economics, 1993, 69(2):138- 146.
[19]Boyle K J, MacDonald H F, Cheng H T, McCollum D W. Bid design and yea saying in single-bounded, dichotomous-choice questions. Land Economics, 1998, 74(1):49- 64.
[20]Roach B, Boyle K J, Welsh M. Testing bid design effects in multiple-bounded, contingent-valuation questions. Land Economics, 2002, 78(1):121- 131.
[21]Ao C L, Chen J T, Jiao Y, Yu S. Non-use Value Evaluation of Sanjiang Wetland in Heilongjiang Province in China. Advances in Information Sciences and Service Sciences, 2013, 5(2):78- 88.
[22]敖长林, 陈瑾婷, 焦扬, 王静. 生态保护价值的距离衰减性——以三江平原湿地为例. 生态学报, 2013, 33(16):5109- 5117.
[23]高琴, 敖长林, 陈红光, 佟锐. 基于居民生态认知的非使用价值支付意愿空间分异研究—以三江平原湿地为例. 生态学报, 2014, 34(7):1851- 1859.
[24]冯磊, 敖长林, 焦扬. 三江平原湿地非使用价值支付意愿的影响因素. 数学的实践与认识, 2012, 24(1):59- 67.
[25]敖长林, 刘芳芳, 焦扬, 陈瑾婷. 三江平原湿地生态价值属性选择分析. 农业技术经济, 2012, (7):87- 93.
[26]Cameron T A, James M D. Estimating willingness to pay from survey data:An alternative pre-test-market evaluation procedure. Journal of Marketing Research, 1987, 24(4):389- 395.
[27]唐克勇, 杨正勇, 杨怀宇, 范晓赟. 上海池塘养殖环境成本——基于双边界二分式CVM法的实证研究. 生态学报, 2012, 32(7):2212- 2222.
[28]Boyle K J, Welsh M P, Bishop R C. Validation of empirical measures of welfare change:Comment. Land Economics, 1988, 64(1):94- 98.
[29]徐钟济. 蒙特卡罗方法. 上海:上海科学技术出版社, 1985.
[30]Zhao J, Liu Q X, Lin L Q, Lü H F, Wang Y. Assessing the comprehensive restoration of an urban river:An integrated application of contingent valuation in Shanghai, China. Science of the Total Environment, 2013, 458- 460(3):517- 526.
[31]Koundouri P, Kountouris Y, Remoundou K. Valuing a wind farm construction:A contingent valuation study in Greece. Energy Policy, 2009, 37(5):1939- 1944.
[32]唐建, 沈田华, 彭珏. 基于双边界二分式CVM法的耕地生态价值评价——以重庆市为例. 资源科学, 2013, 35(1):207- 215.
[33]Alberini A. Optimal designs for discrete choice contingent valuation surveys:Single-bound, double-bound, and bivariate models. Journal of Environmental Economics and Management, 1995, 28(3):287- 306.
[34]杨晋浩. S-PLUS 实用统计分析. 成都:电子科技大学出版社, 2007.
Influence of initial bid number and sample size on the double-bounded dichotomous choice contingent valuation method
AO Changlin*, ZHOU Ling, JIAO Yang, WANG Shixue
DepartmentofManagementScienceandEngineering,NortheastAgriculturalUniversity,Harbin150030,China
Abstract:The contingent valuation method (CVM) is a survey-based method that uses random samples of families or individuals to reveal consumer preferences for goods or services, such as environmental resources, in a hypothetical market. Through questionnaires, CVM identifies people′s preferences and expresses them in dollar terms as willingness to pay (WTP) or willingness to accept (WTA). WTP (or WTA) can be used to gain insights into the potential economic benefits or losses brought about by a planned project. A great variety of questionnaire formats have been developed and applied, among which the dichotomous choice CVM is considered to be one of the most advanced methods. In recent years, the double-bounded dichotomous choice contingent valuation method (DBDC-CVM) has been widely used to value the ecological environment and natural resources. It can identify respondents′ true WTP and reduce the deviation of assessment results, thereby making the results more accurate and reliable. The initial bid number and sample size are very important determinants of WTP in DBDC-CVM. Fewer initial bids and smaller sample sizes will reduce the validity and reliability of the resultant WTP. In contrast, more initial bids and larger sample sizes increases the difficulty and cost of the survey. The number of initial bids is always obtained using a pre-test, while the sample size is always determined by field research or online surveys. This study investigates the dynamic effects of initial bid number and sample size on mean WTP, using the willingness to pay (WTP) function model and a-posteriori Monte Carlo simulation. We use Weibull and log-logistic distributions of WTP to simulate two different sources of data. In order to simplify the Monte Carlo simulation, we quantize the probability distribution and make a hypothesis to design bids. We produce four graphs to visualize the simulated results and use these to identify the optimum number of initial bids and sample size. Initial bid number and sample size had almost the same influence on mean WTP for both WTP distributions. When the initial bid number t and sample size exceed 5 and 500, respectively, the influence on mean WTP is almost the same. Based on this result we suggest that at least 5 initial bids and 500 samples are needed in order to ensure the validity and reliability of estimates of mean of WTP generated by Monte Carlo simulation. These results provide a quantitative basis for CVM questionnaire design and have the potential to improve the validity and reliability of WTP.
Key Words:double bounded dichotomous choice; willingness to pay; Monte Carlo simulation; initial bids content; sample size
DOI:10.5846/stxb201405191024
*通讯作者
Corresponding author.E-mail:aochanglin@gmail.com
收稿日期:2014- 05- 19; 网络出版日期:2015- 06- 12
基金项目:国家自然科学基金资助项目(71171044)
敖长林, 周领, 焦扬, 王世雪.初始投标值数量和样本容量对双边界二分式CVM的影响.生态学报,2016,36(3):854- 862.
Ao C L, Zhou L, Jiao Y, Wang S X.Influence of initial bid number and sample size on the double-bounded dichotomous choice contingent valuation method.Acta Ecologica Sinica,2016,36(3):854- 862.
