液压集成块流道数值模拟分析*
2016-04-13王自勤田丰果陈家兑
雷 琪,王自勤,田丰果,陈家兑
(1.贵州大学现代制造技术教育部重点实验室,贵州贵阳550003;2.贵州大学机械工程学院,贵州贵阳550025)
液压集成块流道数值模拟分析*
雷琪1,王自勤1,田丰果2,陈家兑1
(1.贵州大学现代制造技术教育部重点实验室,贵州贵阳550003;2.贵州大学机械工程学院,贵州贵阳550025)
摘要:应用fluent对液压集成块流道进行分析,得到其直角转弯对压力损失的影响,得出速度和压力分布图,分析不同流速的压力损失,孔径大小对压力损失的影响,以及正反向流的压力损失情况。结果表明:压力损失的主要影响是直角转弯的下流都会形成一处漩涡和流道孔径缩小处对流体的阻力;在同等流量不同孔径的流道中,孔径大小对压力损失比较敏感,在设计允许的情况下,应适当增大孔径;同时改进后的流道,压力损失和气穴得到明显的改善。
关键词:液压集成块压力损失速度分布图
[6]钱锋.粒子群算法及其工业应用[M].北京:科学出版社,2013.
[7]李二闷,卫良保,李扬,等.约束优化的粒子群改进算法及应用[J].太原科技大学学报,2012,33(6):439-440.
[8]梁睦.堆垛机3层货叉直线差动机构的设计[J].起重运输机械,2005(3)32-33.
[9]刘鸿文.材料力学I[M].北京:高等教育出版社,2011.
[10]刘昌祺,董良.自动化立体仓库设计[M].北京:机械工业出版社, 2004.
[11]Shi Y H,Eberhart R C. A modified particle swarm optimizer//Proceedings of the IEEE International Conference on Evolutionary Computation[J].New Jersey: IEEE Press,1998:69-73.
[12]Birge B. Particle swarm optimization toolbox[CP/OL].http://www.mathworks.com/matlabcentral/fileexchange/7506-particle-swarm-optimization-toolbox.2006.
廖源泉(1992-),男,汉族,湖北黄冈人,南华大学机械工程学院硕士研究生,主要研究方向:计算机集成制造系统。
0引言
液压集成块是液压集成必不可少的元件之一,它具有结构紧凑、元件密度高、占据空间小,维护、安装、调整和更换液压元件方便等优点,广泛运用于现代的液压系统中。一般来说,液压集成块的内部孔道,通常采用钻、镗等一般传统的加工方法。采用机械加工的方法一般不能形成流线型流道,直角转弯流道比较多,从而导致流场结构复杂,能量损失增加。液压集成块的内部通油孔道属于典型的复杂空间孔系,在一个块体上纵横交错液压集成块分布着很多个长短、大小不一和位置不同的流道,流道的连接形式可分为短直管路、直角转弯管路、突扩(缩) 管路和交叉管路。本文应用fluent流体软件分析孔径大小和直角转弯对压力损失的影响,为改进集成块流道提供依据[1-6]。
1仿真模拟建立

图1 物理模型
本文是以液压可变配气发动机中液压集成块为研究对象。由于集成化的结构紧凑性,如图1所示,该对象油路集成有7个直角转弯,速度入口通过凸轮推动柱塞运动,在不同转速下液压油的流速都不同,凸轮转速到达2 000 r/min,是一个比较常用和较大的转速,可以作为研究速度,转化到速度入口(孔径为16 mm)流速为1.41 m/s,本文主要是分析流速1.41 m/s换算到孔径为6 mm中流速为10 m/s。
2液压集成块内部流道的数学模型
液压集成块内部的液流为粘性不可压缩流体,液流在直角管道转向处多数情况下为湍流流动[7],因此采用标准k-ε湍流模型控制,具体控制方程[8]如下:
(1)连续性方程
(1)
式中:u,v和w为速度矢量在x,y和z方向的分量。
(2)动量(Navier-Stokes)方程
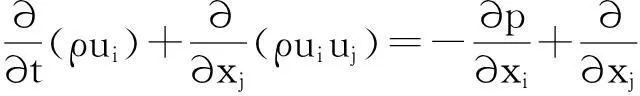
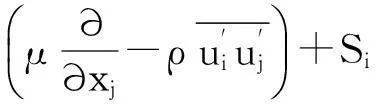
(2)

(3)标准k-ε方程
(3)
式中:μ1为湍动粘度;Cμ为经验常数,这里取Cμ=0.09;k为湍动能;ε为湍动耗散率。
(4)湍动能k的输运方程
(4)

(5)耗散率ε的运输方程
(5)
式中:C1ε、C2ε、σε为经验常数,C1ε=1.44,C2ε=1.92,σε=1.3。
3网格划分与边界条件设置
用UG画出三维图,导出step格式,将step格式导入Gambit中,对其进行网格划分,网格单元采用Tet/Hybird,网格类型采用TGrid[9],定义其边界的速度进口,压力出口,导出mesh文件。在fluent软件中设置速度入口(1.41 m/s)和压力出口(0 Pa),液压油密度866 kg/m3,动力粘度0.013 kg/m·s。湍流模型选择标准k-ε模型,监视窗口设置速度进口、压力出口为面监控(Surface Monitors),选择类型为区域重量平均(Area-Weighted Average),其他设置不变[10]。
4仿真结果及分析
对速度入口设置流速为1.41 m/s,出口压力设置为0 Pa,仿真结果如图2所示,从图中可以看出,速度分布图,在速度入口管径为16 mm的,流线基本是一致的,比较稳定,没有出现漩涡;液压油由孔径为16 mm流入孔径为6 mm的流道中,流速分布相对比较均匀,从图中直角转弯1处有较小的漩涡,影响压力损失的主要原因不是漩涡。同时可以在直角转弯2-7处的流速图得出,在直角转弯的下流都会产生一个漩涡,且产生的漩涡比直角转弯1处程度要大很多,同时管内的流速分布不均匀,最大流速主要分布在漩涡处的上面,说明管内流速不均匀主要是漩涡造成的,漩涡程度越大对其流速分布不均匀影响越大,流线密集程度越高,压力损失越大。

图2 速度分布图
如图3所示,为中心对称压力分布图,从图中可以看出入口压力基本恒定为0.528 MPa,出口压力为0,说明入口速度为1.41 m/s,管内压力损失为0.528 MPa,根据实验数据孔内的最大油压为6.3 MPa,压力损失占系统油压8.38%,对系统有一定影响。同时得出管径16 mm的导管内的压力损失较小;对其直角转弯处的压力损失进行分析,以X轴的导管长度(单位mm),以Y轴为压力图,同时取轴的中心对称的压力分布图的压力损失,对其作出如图4所示,图中的序号代表每一处直角转弯,从图中分析可以得出,1处的直角转弯压力损失最大,说明孔径缩小压力损失最大为0.06 MPa,对流体压力损失较大,其能量消耗在孔径缩小的流体阻力上;同时从图中还可以得出,直孔对液体压力损失较小;直角转弯处的下游都会形成一处漩涡,在3和4处的之间的直管的压力梯度大,形成的漩涡的强度最大,这主要是两处直角转弯间的距离较小造成的,最大梯度油压差0.12 MPa;在7处的漩涡出现负值,容易出现气穴等不利于集成导管的现象。
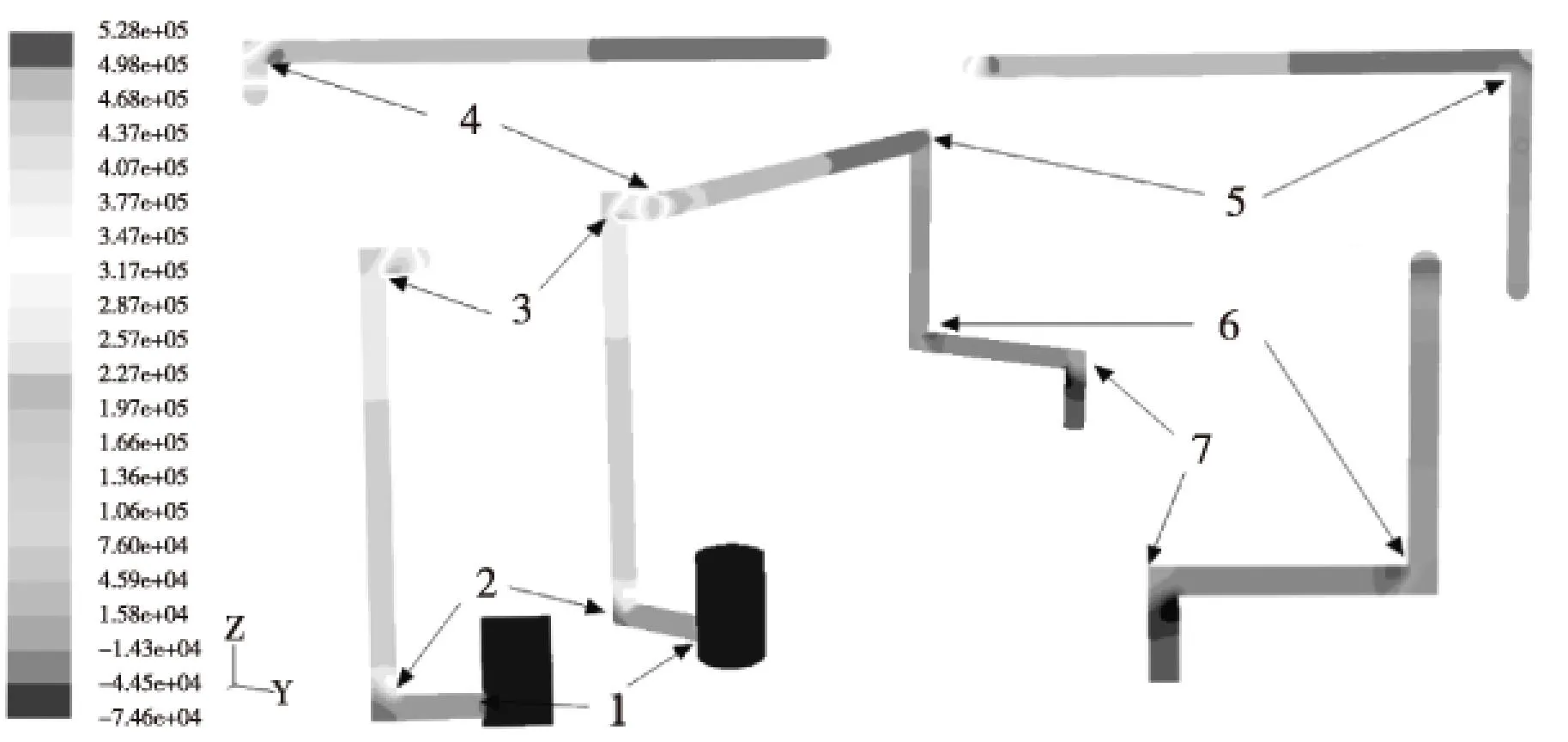
图3 压力分布图

图4 直角转弯压力损失图
5集成流道孔径大小对流场的影响大小
当集成油路进口速度为1.41 m/s,孔径为16 mm不变,对油路集成部分的孔径分布设置为4、5、6、7、8 mm进行分析,得出压力损失分别为2.687 MPa、1.072 MPa、0.528 MPa、0.293 MPa、0.176 MPa,得出图5,从图可以得出,孔径的大小对流场压力损失影响很大,也很敏感,主要是孔径大小影响孔内流速,当孔径减小时,孔内流速增大,同时在孔径缩小处对压力能量损失更大,在直角转弯处形成的漩涡更明显,更剧烈。
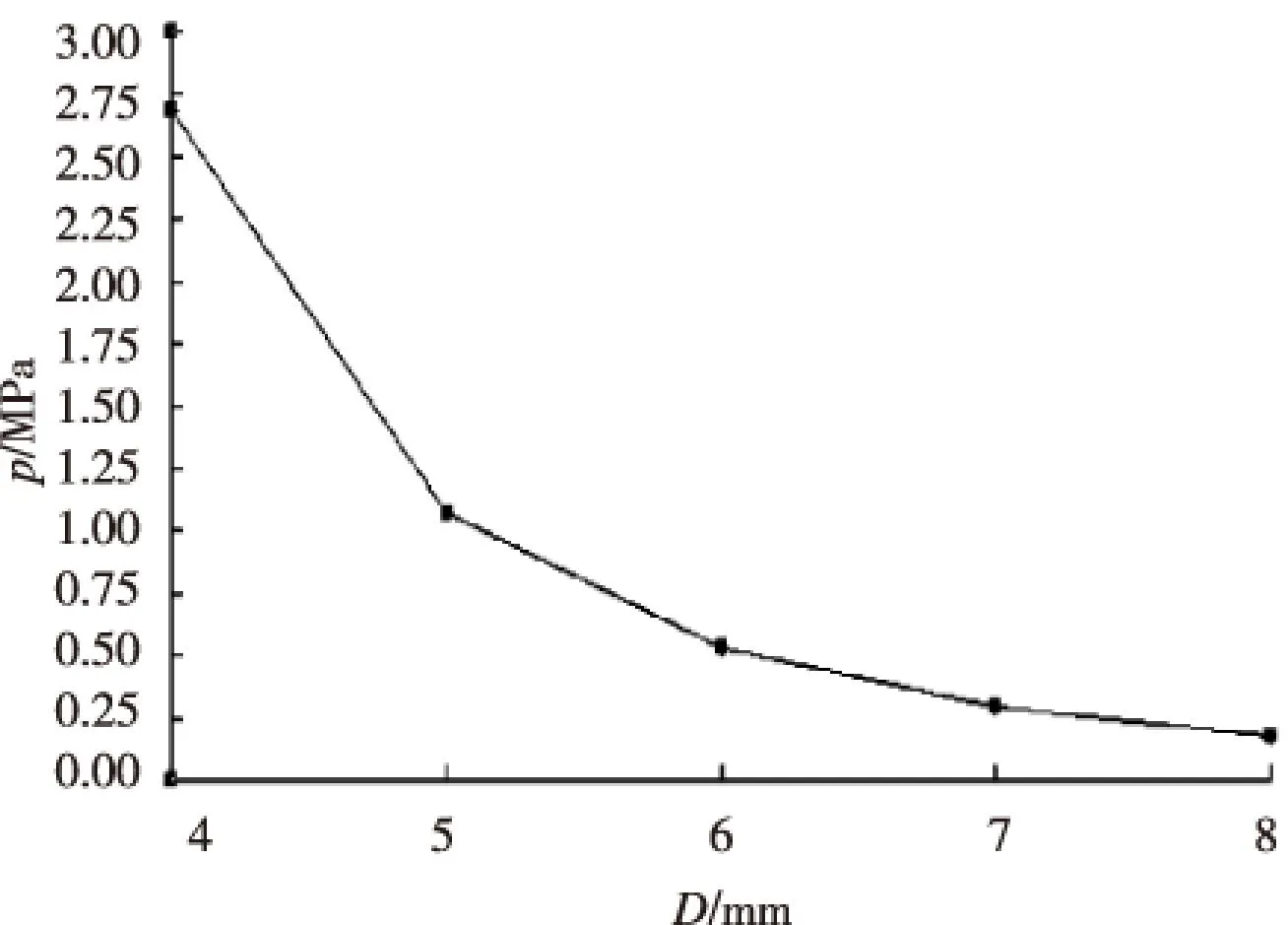
图5 不同孔径的压力损失图
6集成流道不同流速的正反向流的压力损失
集成油路孔径6 mm的流速设置为1 m/s~10 m/s,正向流即液压油(图1)从速度入口流入,反向流即(图1)从压力出口流入,并在fluent中调整其相关边界条件,得到不同流速的压力损失,如图6所示,正向流的压力损失要比反向压力损失要大,且基本为定值,主要是正向流在孔径缩小处损失的能量要比反向流在孔径增大处的大。

图6 正反向流的压力损失图
7集成流道直角转弯处改进设置
集成油路主要是工艺孔产生的直角,压力损失主要由直角转弯处造成的,如果改善其相交直角转弯处为一定的曲率半径,设置其曲率半径10 mm,则得出孔径(6 mm)在1 m/s~10 m/s的压力损失,与不改进的压力损失进行对比,如图7所示,可以得出直角弯角处改进成10 mm曲率半径,压力损失明显减少,随着流速越大压力损失减少的越明显。同时改进后速度流线分布图,如图8所示,可以得出速度流线分布比较均匀,没有出现漩涡,这有利于流体运动状态,减少压力漩涡带来的压力损失。最大压力损失是0.29 MPa,占系统最大压力的4.6%,可以看出得到明显的改善。
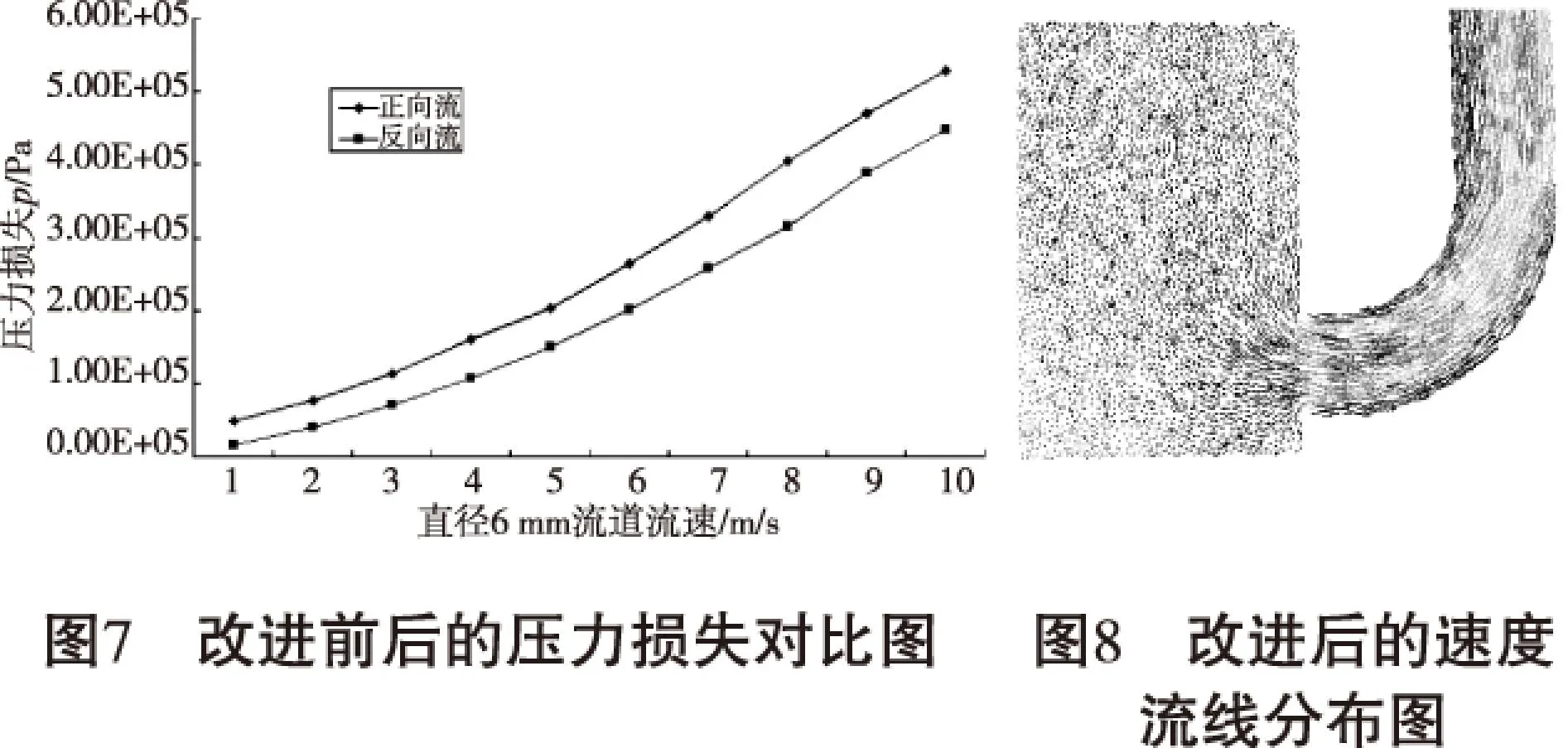
8结论
1)在直角转弯的下游都会形成一个漩涡,这是压力损失的主要原因,在孔径缩小处压力损失最大,主要是能量消耗在孔径缩小的流体阻力上。
2)油路孔径大小对压力损失影响很大,在设计时应适当加大孔径,适当减少孔径突缩。
3)集成块流道应适当减少直角转弯,多使用曲率转角,有利于减少压力损失,同时减少流道转角处的漩涡和气穴等不利现象。
4)流道改进前的压力损失为0.528 MPa,占系统总压的8.38%,改进后的为0.29 MPa,占系统总压的4.6%,得到明显的改善。
参考文献
[1]谢国庆,李运初. 基于Fluent的液压集成块典型流道流场仿真分析[J]. 液压与气动,2013(12)44-47.
[2]高殿荣,王益群.液压集成块内弯曲流道流场数值计算与分析[J].机床与液压,2001(6)34-35.
[3]任小中,崔凤奎,王晓强.液压集成块计算机辅助设计[J].农业机械学报,2000,31(5):97-99.
[4]李海龙,高殿荣. 基于Fluent液压集成块内部流道流场的数值模拟[J]. 液压与气动,2011(03)1-4.
[5]吴正坤,赵毅红,吕宵宵,黄博文. 基于Fluent液压集成块内部流场数据仿真[J]. 机械工程与自动化,2014(06)76-77+80.
[6]袁昌耀,傅连东,王佳,刘龙园,陈忱. 基于FLUENT液压集成块管内数值仿真[J]. 机械,2008,35(12):16-18.
[7]Hughes W F,Brighton J A.流体动力学[M].徐燕侯,过明道,徐立功,等译.北京:科技出版社,2002.
[8]王福军.计算流体动力学分析—CFD 软件原理与应用[M].北京: 清华大学出版社,2004.
[9]韩占忠,王敬,兰小平. FLUENT 流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社,2004.
[10]张凯,王瑞金,王刚. Fluent技术基础与应用实例[M]. 北京: 清华大学出版社, 2010.
王自勤(1954-),男,贵州贵阳人,教授,博士生导师,主要研究方向:发动机可变气门驱动技术,机械制造。
Numerical simulation analysis of pipeline of hydraulic manifold block
LEI Qi,WANG Ziqin,TIAN Fengguo,CHEN Jiadui
Abstract:This paper analyzes the pipeline of hydraulic manifold block with fluent in order to examine how its quarter turn affects the pressure loss, and work out the velocity and pressure profile. It is also investigated how different flow velocity, aperture size,and flow direction influence the pressure loss. The results show that: the main cause of the pressure loss is from the vortex at the lower part of the quarter turn and the narrower part of the pipe, both of which produce resistance to the fluid; and the aperture size apparently affects the pressure loss at the same flow rate. If the design allows, it is desirable that the aperture be properly enlarged. The pressure loss is decreased and cavitation improved after the optimization of the pipeline.
Keywords:hydraulic manifold block; pressure loss; velocity profile
收稿日期:2015-07-21 2015-07-14
通讯作者:刘琼(1980-),男,汉族,湖南衡阳人,南华大学机械工程学院讲师,博士,主要研究方向:计算机集成制造系统。
作者简介:陈俊明(1989-),男,湖南永州人,南华大学机械工程学院硕士研究生,主要研究方向:现代设计理论与方法。 雷琪(1989-),男,湖南郴州人,在读硕士,主要研究方向:发动机可变气门技术和CAE技术。
基金项目:南华大学科研启动基金资助项目(2007XQD35,2014XQD43);湖南省自然科学基金资助项目(10JJ4037)。 贵州省科技厅贵州大学联合基金(黔科合LH字[2014]7626)。
中图分类号:TP391.9;TH137.9
文献标识码:A
文章编号:1002-6886(2016)01-0019-04
