铁路桥梁桩基承台力学分析及配筋探讨
2016-04-13汪鹏翔
汪鹏翔
(中铁工程设计咨询集团有限公司,北京 100055)
铁路桥梁桩基承台力学分析及配筋探讨
汪鹏翔
(中铁工程设计咨询集团有限公司,北京100055)
Railway Bridge Pile Cap Mechanical Analysis and Discussion Reinforcement
WANG Pengxiang
摘要现行铁路设计规范提出承台的厚度及配筋应根据受力情况确定,在条文及条文说明中提出厚度、混凝土强度、刚性角、底面钢筋面积等要求,但没有明确承台计算方法。依托实际工程项目,对典型承台在不同桩间距、桩基刚度情况下进行受力分析。对比有限元模型计算结果与现行国内外比较通行的建筑、公路规范的计算结果,结合国内常规铁路桥梁承台设计的经验,提出经济、合理的承台配筋设计计算方法。
关键词铁路桥梁桩基承台配筋计算方法
1概述
对于桩基承台的设计计算,国内建筑地基规范、建筑桩基规范、美国规范(ACI318-02)采用“悬臂梁法”,即将承台视为一般悬臂梁,根据实验得到的破坏特点,按钢筋混凝土结构进行受弯、受剪、受冲切计算,国内公路规范(JTG62—2004)在桩间距相对较大的情况下也采用这种受力模式。当桩间距相对较小时还引入美国公路桥梁规范《AASHTO LRFD Bridge Design Specifications,CustomaryU.S.Units》,按空间桁架模型进行承台设计,按“撑杆-系杆体系”进行承台计算。
国内铁路承台设计采用控制刚性角、顶底面设置纵横向钢筋的办法保证承台安全。随着我国大量高标准客运专线的建设,铁道部曾发布的铁建设函[2006]338号《关于发布客运专线铁路加强抗震设计技术要求的通知》(已废止)规定:“承台采用六面配筋,顶面钢筋的直径不应小于16 mm、间距不应大于15 cm;底面钢筋的设置应根据受力计算确定,其余四面按构造要求配筋”。近年来客运专线及部分客货共线铁路桥梁的承台基本参考此标准来进行设计。多年的实践结果也表明此方法是安全可靠的,但长期以来一直没有给出合理的理论计算支撑。
2研究方法
承台计算的两个主要问题:一是考虑受冲切、受剪、撑杆确定承台厚度;其次按悬臂梁法或系杆计算承台底的受拉钢筋数量。对于抗冲切和抗剪的分析评价,需要进行大量的试验工作。按现行铁路规范的要求,铁路桥梁承台一般具有较大的厚度,抗冲切抗剪不控制设计。以下对冲切、抗剪以及基于耐久性方面考虑的承台侧面构造配筋不做探讨,而着重对受计算控制且配置较多的承台底面钢筋设计进行论述。
承台结构受力模式在本质上可以理解为“墩底荷载作用于数个支撑点的钢筋混凝土厚板”。通过分析国内外常用的计算理论,建筑与公路承台受力模式基本明确,计算理论成熟,在力学性能与铁路桥梁承台有较多共同点,在计算方法和思路上公路承台与铁路承台尤为相近。因此,本次研究通过建立承台的有限元模型进行受力分析,并按现行铁路钢筋混凝土结构进行配筋计算,由此进一步考察验证各种理论计算方法应用于铁路桥梁承台设计的可行性。
计算过程以实际工程应用中某特定工况下某类型承台为代表,在荷载与承台厚度不变的情况下,分析影响承台底面配筋的两个主要因素,即桩基刚度和桩间距。
3有限元模型建立
选用某客运专线典型12桩承台进行有限元计算,该种承台应用于多种地质条件中,承台厚3 m,共12根直径1.25 m摩擦桩;有限元计算采用通用的Ansys软件,选用Solid95单元建立空间实体模型。承台底建立1 m桩长,承台顶部建立1 m高度墩身,桩底采用combin14单元施加弹性约束,墩顶部施加典型荷载(竖向力41 814 kN;横向作用时横向水平力760 kN、横向弯矩35 315 kN·m;纵向作用时纵向水平力604 kN、纵向弯矩16 587 kN,其余荷载为0,分别计算横向作用和纵向作用)。桩底约束包含桩底竖向弹性约束和水平固结约束,有限元模型单元如图1所示。
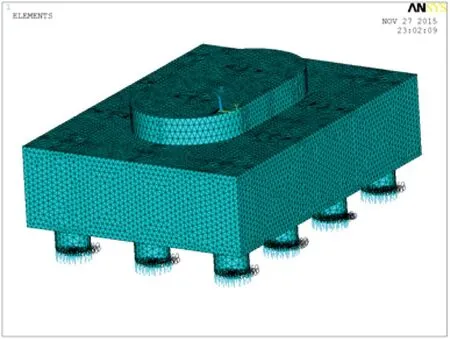
图1 承台单元模型
4不同桩基刚度下承台有限元模型分析
4.1桩基刚度
承台底桩基竖向刚度包含桩基自身压缩变形和桩底地基压缩变形产生的抗力,单位荷载下压缩变形分别用Se、Sb表示。则承台底桩基竖向刚度为
式中l——摩擦桩计算弹性刚度部分长度;
ξ——与桩侧阻力分布相关的系数,柱桩时ξ=1,摩擦桩取小值ξ=0.5;
E、A——分别为桩截面材料弹性模量、面积,C30混凝土取用E=3.2×104MPa;
C0——基底竖向地基系数,摩擦桩土质地基C0=m0l。m0为桩底竖向地基系数随深度线性增大的比例系数;柱桩根据地质条件C0取300~15 000 MPa/m;
A0——桩底平面地基的受压面积,对于一般的铁路桥梁承台摩擦桩,A0为以桩间距为直径的圆形面积;柱桩A0=A。
由以上公式可知,在实际工程中,以下情况承台底桩基分别有最大和最小的刚度:(1)当桩长l取极限值0,C0取极大值时得到最大刚度K=C0A;(2)由刚度公式可推算桩间距、地基条件m0取值与桩基刚度均成正比。取最小的桩间距2.5d和m0=10 000 kPa/m2,桩长32 m以下桩基刚度随桩长梯增且在32 m时达到最大值,桩长大于32 m后刚度梯减。考虑到1.25 m桩径的摩擦桩常用取值范围,取桩长10 m时有最小刚度。桩基竖向刚度均介于上述最大和最小刚度之间,Ansys模型按从大到小依次取8种不同桩基竖向刚度,刚度取值及对应的参数m0和桩长l值如表1所示。

表1 不同地基刚度对应的地基参数
4.2不同刚度桩基有限元计算结果
(1)承台底面应力分析
图2为纵向作用时顺桥面沿承台中心剖切得到的承台正应力云图。计算结果表明,在断面中承台上缘受压,下缘受拉,中间应力趋近于0,受力基本均匀,符合平截面假定。横桥受力极不均匀,桩中心连线处应力明显要大于中间切不到桩的断面,承台中间墩底部分应力要明显大于边桩范围内的应力。而工程实际中,承台底面配筋基本采用均匀分布的方式,较少采用桩基连线部分加强的方式。
考虑到应力横向分布的不均匀性,配筋计算采用两种方式将模型中实体结构应力分布转化为截面内力。(1)桩反力反算法:采用Ansys软件中积分功能得到各桩反力,选用最大外排桩的实际反力代表全部外排桩计算截面内力,此方法既考虑了桩反力的不均匀分布,也能得到相对保守配筋截面内力。(2)应力换算法:用底部极限拉应力换算截面内力,此种方法将受力较小的位置均用极限值来进行计算,比实际计算内力要偏大,工程应用偏于保守。如表2所示,采用最大应力换算得到的弯矩要大于按桩反力计算得到的弯矩,横向内力相对接近与截面位置未考虑上部桥墩有关。在后文桩间距对比计算中,按两种计算结果与规范计算结果均进行对比。
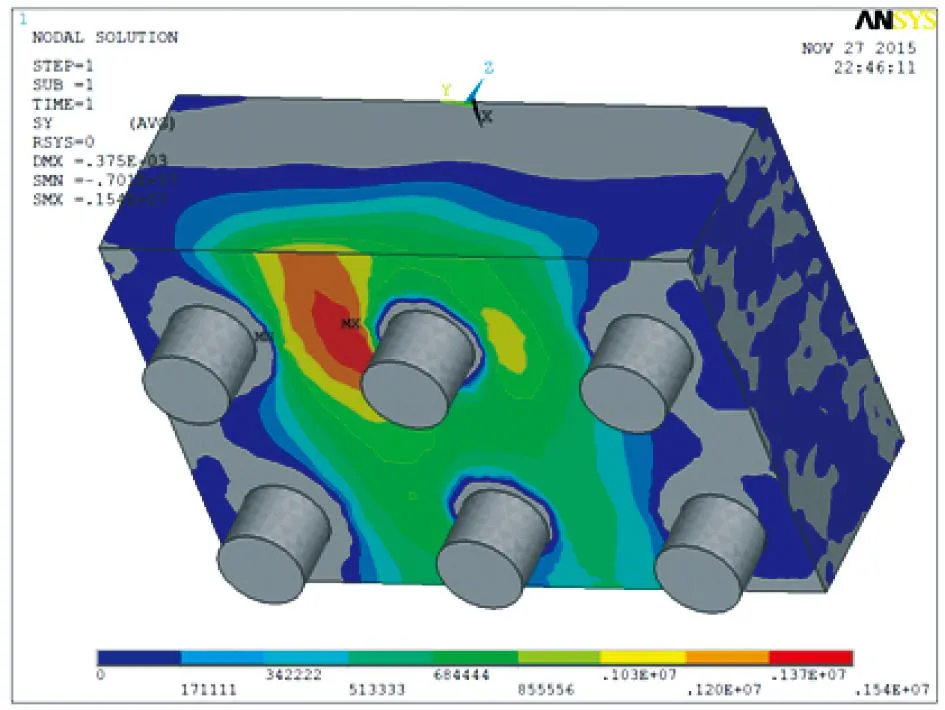
图2 半承台顺桥向作用正应力云图
(2)桩底反力分析
除了横向应力分布的不均性,各桩的支反力也呈现很大的不均匀性。以纵向作用为例(如图3所示):图3(a)为理论计算桩底反力分布,图3(b)为有限元计算桩底反力分布云图。理论计算公式均假定承台为刚体,模型计算由于考虑到承台的弹性刚度,在墩底竖向力和弯矩作用下,墩底部分桩基受较大竖向力,通过承台传递至外围的桩受较小竖向力。不论桩基刚度取极大值或极小值,桩基反力受此影响明显,且桩基刚度在工程范围内变化时,桩基反力无实质变化。如表2所示,最大刚度与最小刚度比较下桩基反力差值小于15%,承台底部应力正常范围小于5%。由此可以判断在一般地质条件中,无论是桩长变化还是地基条件变化对承台的配筋没有实质性的影响。
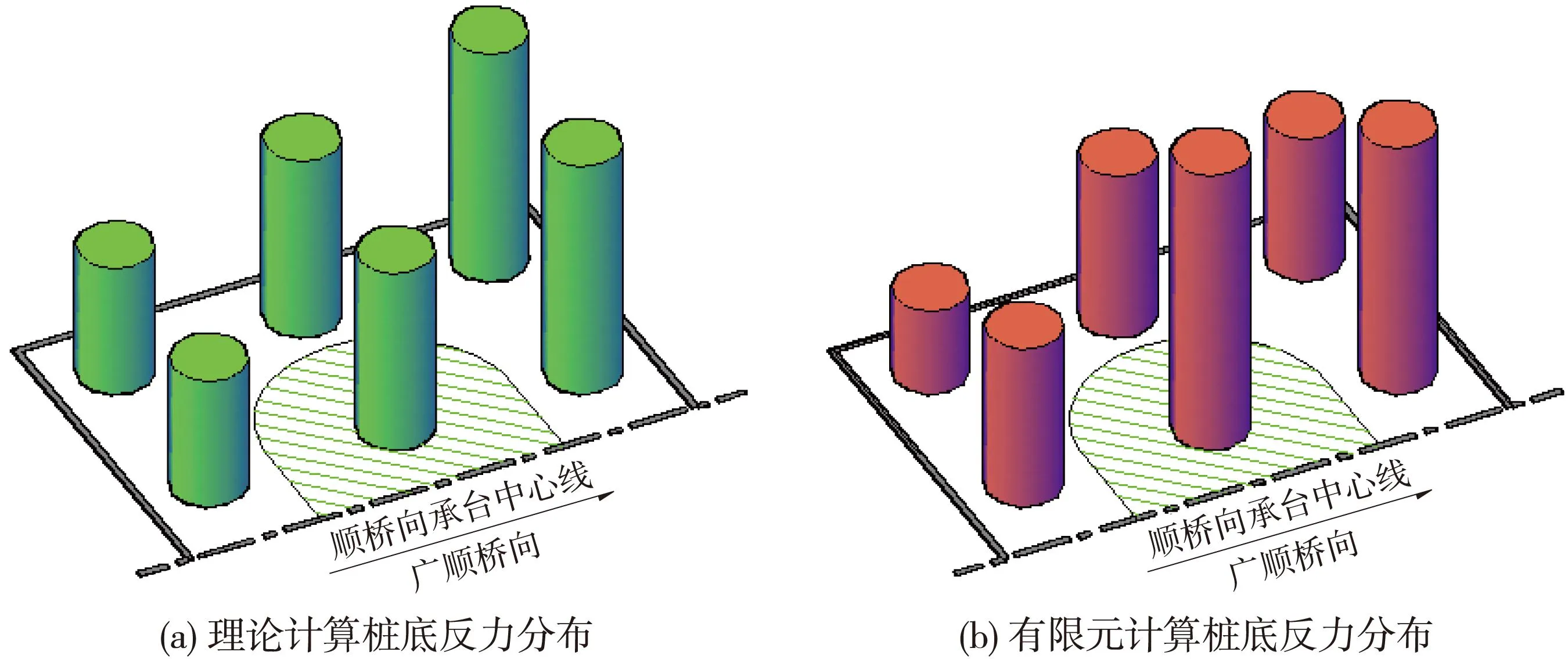
图3 桩基反力对比柱状示意
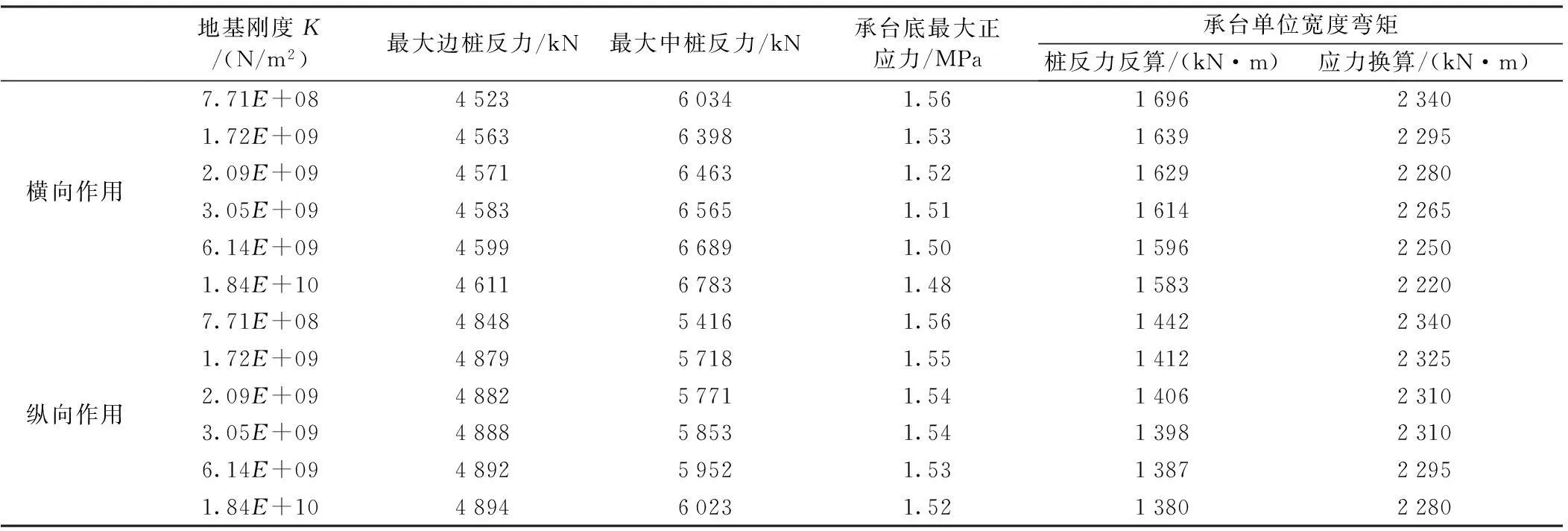
横向作用纵向作用地基刚度K/(N/m2)最大边桩反力/kN最大中桩反力/kN承台底最大正应力/MPa承台单位宽度弯矩桩反力反算/(kN·m)应力换算/(kN·m)7.71E+08452360341.56169623401.72E+09456363981.53163922952.09E+09457164631.52162922803.05E+09458365651.51161422656.14E+09459966891.50159622501.84E+10461167831.48158322207.71E+08484854161.56144223401.72E+09487957181.55141223252.09E+09488257711.54140623103.05E+09488858531.54139823106.14E+09489259521.53138722951.84E+10489460231.5213802280
5桩间距变化承台受力分析
保持承台厚度不变,顺桥向作用下分别增加顺桥向桩间距,桩间距依次取3.3 m、3.8 m、4.3 m、4.8 m,建立有限元模型进行分析,桩底弹性系数取摩擦桩m0=40 000 kPa、L=40 m,K=1.72×109N/m2。主要计算结果如表3所示。
从各有限元应力计算结果中可以看出,有限元计算应力分布随着桩间距增加,各方向正拉应力增加,应力分布相对趋于均匀,但应力极值增幅减小,刚性角超过45°时,最大应力小于1.9 MPa,外排桩反力变化趋势与理论计算相符。
四种配筋计算方法得到单位宽度承台底面配筋面积均随桩间距增加,这与实际情况相符。随桩间距增加配筋面积曲线如图4所示。对比有限元计算钢筋面积,当桩间距增大,采用应力换算法钢筋面积增幅小于采用桩反力算法。理论计算方法中撑杆-系杆法计算面积大于悬臂梁法计算面积。
当刚性角小于35°的情况下,撑杆-系杆法计算得到的配筋面积仅小于有限元应力换算法得到的配筋面积,考虑到在较小的桩间距情况下应力分布的不均匀性而导致有限元应力换算法得到的钢筋面积偏大,可知撑杆-系杆法在小于35°情况下得到的结果是保守的。
当刚性角大于35°后,有限元计算钢筋面积均大于理论计算面积,桩间距越大则角桩越“边缘化”,受到竖向力越小,有限元计算结果验证了这一点。采用桩反力换算法时,用受力较大的边桩进行承台截面内力计算,其配筋结果偏大。因此,当桩间距大于40°时,承台底面纵、横向钢筋穿过桥墩在底面上的投影部分钢筋面积应适当增加,而外围钢筋应适当减少,如底面均匀配筋则应在理论计算结果上应适当增加配筋面积10%~20%。
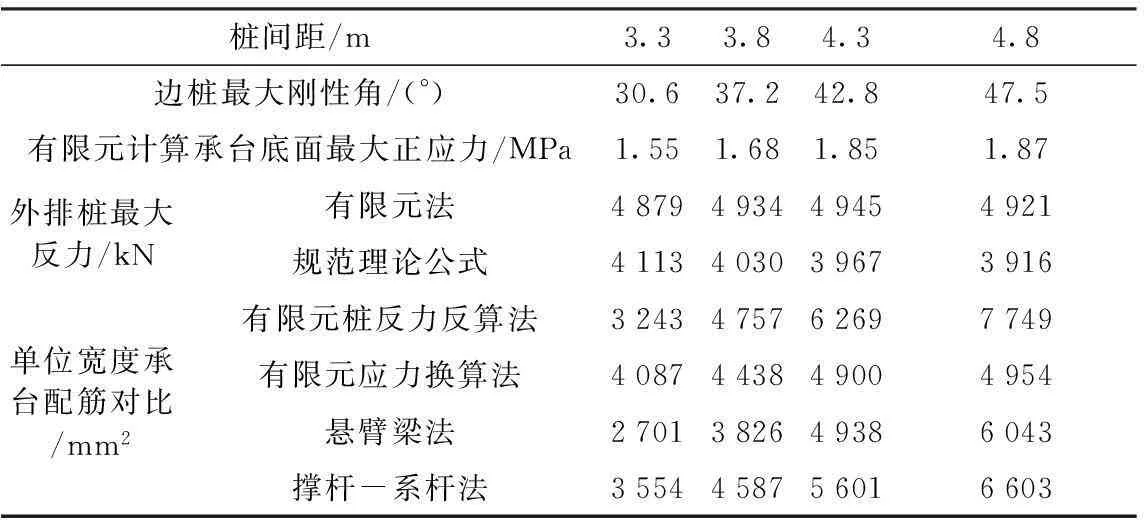
表3 不同桩间距主要计算结果对比
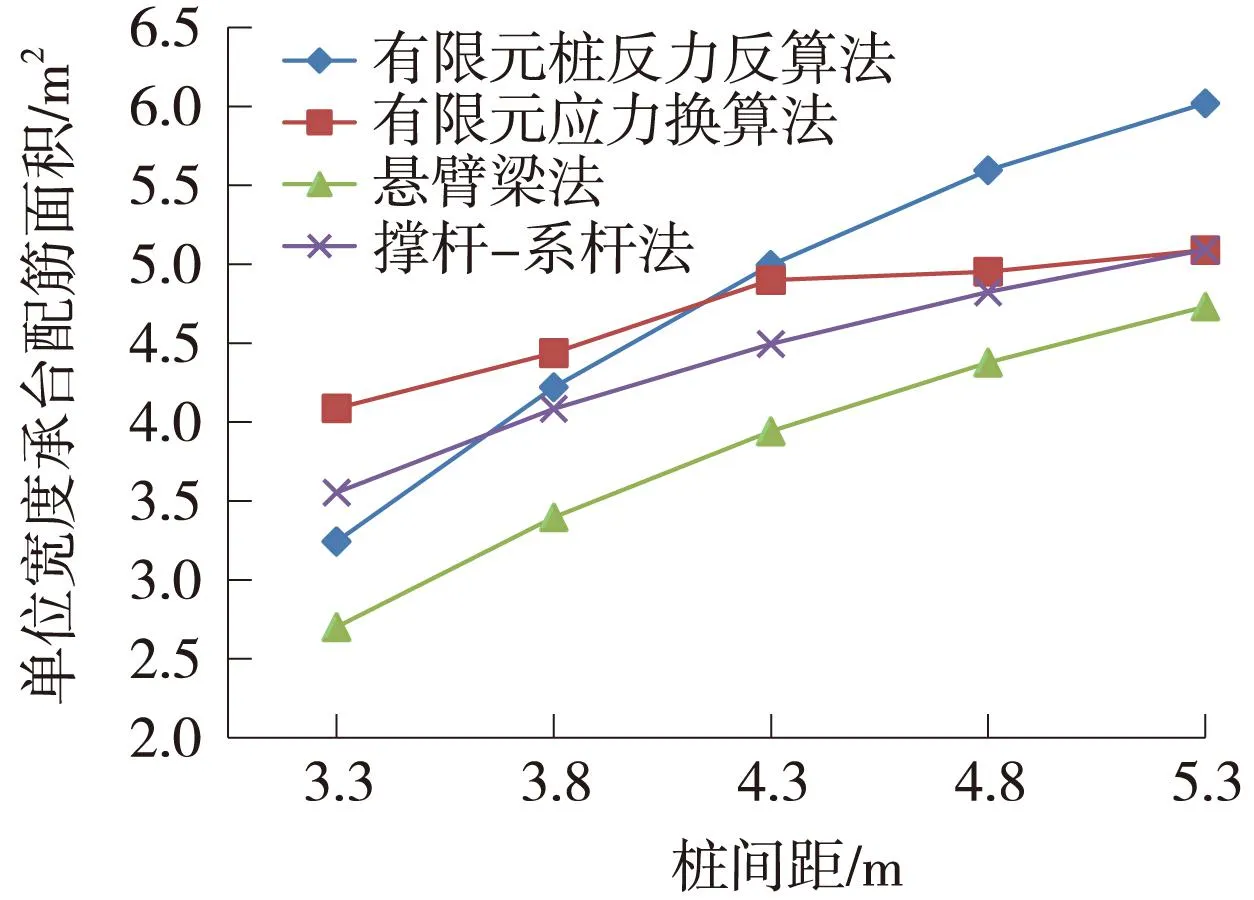
图4 单位宽度配筋面积对比
6结论
(1)对八桩承台、十桩承台,以及不同厚度、桩径承台计算可以得到类似结果。当满足35°刚性角要求时,采用公路撑杆-系杆法计算钢筋面积是安全可靠的,按国内外研究结论,相比悬臂梁法也更适用于刚性角较小的承台计算。
(2)铁路规范条文说明中1 m宽度配1 500~2 000 mm2钢筋,对于外排桩反力较大的承台,仅按此标准不能满足计算要求。无论采用有限元计算或是采用理论计算方法,承台底面钢筋配置都与外排桩的反力有直接的关系。控制承台底面配筋与控制外排桩反力实质相同。
(3)在保证承台不会因桩顶反力增加而产生受压破坏的情况下,可采用增加底面配筋来提高单桩反力限值。
(4)有限元计算结果表明,相同的承台结构在不同的地质和不同的桩长下,受力区别不大。但有限元计算考虑了承台的变形,与理论计算假定承台为刚性不同,直接导致承台的受力以及桩顶反力分布不同。实际计算中越靠近桥墩桩反力越大;对于桩间距较大的承台底面配筋可适当密布于桩连线处以及桥墩水平投影范围。
(5)相同荷载下,桩间距增加时,单桩反力得到减少,但承台尺寸和钢筋量均有较大的增加,在设计时应充分衡量增加桩数量减少桩间距与仅增加桩间距两种方式的利弊。铁路承台设计比较常用的采用35°刚性角来控制设计兼顾承台及桩的受力,是经济合理的。
参考文献
[1]刘金砺,高文生,邱明兵.建筑桩基技术规范应用手册[M].北京:中国建筑工业出版社,2010
[2]叶栋,刘鹏,妥鹏.铁路桩基承台的撑杆-系杆体系及承载能力研究[J].兰州交通大学学报,2014,2(1):131-137
[3]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007
[4]李文会.桥梁桩基承台的受力分析[J].都市快轨交通,2005(3):59-62
[5]王昕.关于桩基承台计算的讨论[J].辽宁交通科技,2005(10):36-37
[6]马宗中,周克荣.承台传力机理及设计方法研究[J].结构工程师,2006(3):8-10
[7]张夫健.铁路桥梁群桩基础沉降性状与计算分析[J].铁道勘察,2012(3):75-77
[8]庞竞拓.桩基下溶洞顶板安全厚度有限元计算分析[J].铁道勘察,2014(6):50-53
[9]TB10002.2—2005铁路桥涵地基基础设计规范[S]
[10]JTG D63—2007公路桥涵地基与基础设计规范[S]
[11]GB 50007—2011建筑地基基础设计规范[S]
[12]TB10002.3—2005铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S]
中图分类号:U443.25; TU755.3
文献标识码:B
文章编号:1672-7479(2016)01-0107-04
作者简介:汪鹏翔(1983—),男,2010年毕业于石家庄铁道大学桥梁工程专业,工学硕士,工程师。
收稿日期:2015-12-11
