梁桥模态参数图像识别技术的模型试验研究

胡朝辉　袁向荣

(1.广州诚安路桥检测有限公司，广东广州　510420； 2.广州大学，广东广州　510000)



梁桥模态参数图像识别技术的模型试验研究

胡朝辉1袁向荣2

(1.广州诚安路桥检测有限公司，广东广州510420； 2.广州大学，广东广州510000)

Models Test Study on Modal Parameters of Beam Bridge by Image Processing Technique

HU Zhaohui1YUAN Xiangrong2

摘要介绍一种非接触式视频图像梁桥振动检测方法，利用图像识别技术与小波分析方法，以MATLAB软件构建测试系统，对某简支梁模型进行振动测试。以数码摄像头采集模型梁振动的视频图像，通过计算机将采集的视频分解为时间-图像序列，然后采用图像边缘检测法对图像序列进行处理分析，可得到梁振动的位移-时间数据。对振动信号进行Morlet连续复小波变换，进而识别出梁模型的模态参数，测试结果与FFT分析结果比较一致，验证了视频图像测试方法的可靠性和准确性。

关键词数字图像处理边缘检测小波分析简支梁模型模态参数

目前，梁桥的振动检测主要测试其固有频率、阻尼比、振型等动力特性参数，常规方法主要采用加速度、速度及位移传感器结合有线或无线采集系统进行振动测量，记录及分析，是目前解决振动检测问题成熟且可靠的检测方法，因其属于点式检测故而检测数据有限。与之相比，基于图像测量技术的检测手段则属于线式或面式检测，不仅数据完备，而且为非接触式检测。近年来，已有众多学者将该技术应用到遥感测绘、结构静变形检测、动态挠度监测、破损检测、索结构振动检测等领域。例如摄影测量在土地测绘中的应用[1-3]；黄文等采用图像边缘检测法对索结构进行振动检测[4]，识别了索结构的振动频率；袁向荣等采用数字图像相关法进行梁的变形检测和破损检测[5-6]；王翔等基于图像识别技术研究采用高速相机检测桥梁的动态挠度[7]。

基于视频图像测量原理和小波分析技术，以MATLAB软件构建视频图像测振系统。首先采用该测试系统采集梁振动的视频，将视频分解为时间图像序列，进行分析处理得到位移-时间曲线。在后处理中对梁的振动信号进行Morley连续复小波分析，由分析所得的一系列小波系数识别出梁的固有频率、阻尼比和阵型，将分析结果与FFT分析结果进行比较，以验证该方法的准确性。

1图像识别技术测试系统

基于MATLAB软件平台设计了针对模型试验的测试系统，由硬件系统和软件系统两部分组成(见图1)。

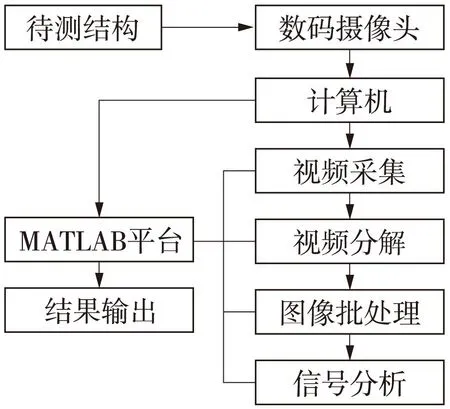
图1　视频图像振动测试系统

结构变形图像识别原理:以结构变形前的图像作为参考图像，将变形后的图像与参考图像进行比较，计算特征区域的变化，经换算后得到结构的变形。

以某梁模型的一维竖向振动来对测试方法的原理加以说明，图2为某简支梁处于平衡状态和某一变形状态的两幅灰度图像，记为平衡状态与变形后状态。对两幅图像的边缘灰度采用边缘检测算法进行求解，可以得到边缘的亚像素位置。由两幅图像所得出的亚像素边缘位置之差，得到梁变形后的位移，然后通过像素的标定换算，得到梁变形后的位移。进行振动测量时，先采用视频采集设备获取梁振动的视频，而后将视频分解为图像序列，利用上述方法对梁振动时每一状态所对应的每幅图像进行边缘检测处理，可得到梁上各点处的动态位移。由变形后图像与采样间隔的关系，可得到位移时间信号，然后对梁上各点的位移时间信号进行频谱分析，即可识别频率、阻尼比、振型等参数。

图2　简支梁两种状态下的灰度图像

2动态位移与模态参数识别原理

2.1变形检测图像识别方法

目前，图像法变形检测主要采用数字图像相关法和边缘检测法，这里采用数字图像边缘检测法。目前应用较多的为多项式拟合法，多项式拟合法计算量较小且计算精度较好，其公式为

I(z)=c0+c1z+c2z2+…+c5z5

上式中：z为边缘附近像素点的位置，I为z点处的灰度值，c0…cn为多项式系数；采用5阶多项式拟合边缘灰度，用Sobel算法获取边缘附近一系列像素点位置及灰度值，将其代入上述多项式，求解待确定的系数c0～c5

灰度变化明显的边缘位置由下式确定

由上式求得边缘位置z，然后根据变形前后两幅图像边缘点位置z值之差求得该像素点处的位移。

依次对每幅图像的边缘进行定位并求得位移，则某像素点某个时刻的位移可记为yi(t)

实际检测中，结构的振动过程是连续的，而通过摄影设备拍摄的视频是由离散的图像序列组成，即

i=1，2，…nt

上式中T为采样周期，ya(t)为位移时间信号，可见，利用视频图像进行振动检测同样需要满足采样定理的要求，因此视频设备的采用频率越高，则测试范围越大。

2.2小波变换识别模态参数原理

单自由度黏性阻尼系统的脉冲响应函数[8]为

式中A为残余振幅，ωn为无阻尼固有频率，ωd为有阻尼固有频率，φ0为初相角，ζ为阻尼比。

其Morlet复小波变换为[9]

对于给定的尺度值ai[10]，小波变换系数的模及幅角为

当ai=2πfc/ωd时，小波系数的模在整个时间域中取极值，此时有

从尺度ai=2πfc/ωd下的小波变换模在半对数刻度上的直线斜率以及小波变换幅角的直线斜率可以识别无阻尼固有频率和阻尼比。

对于多自由度线性系统，某一自由度的脉冲响应等于各阶模态的叠加，即

其小波变换为

当ai=ω0/ωdi时，在相邻频率间隔比较大的情况下，第i阶模态对小波系数的贡献最大，其它模态对应的小波系数幅值很小，可不计其影响，小波系数近似表达式为

这时在ai=2πfc/ωdi处，小波系数取得局部极值，进一步可识别出模态频率和阻尼比，模态振型则由各点在各尺度下模取极值时的小波系数经拟合确定

式中WTk、WTl分别为参考点k与测点l对应第i阶模态小波变换系数。

3试验及结果分析

3.1试验模型

试验设计了两种模型，梁长为1.2 m，截面为槽形，材料匀质，质量不计，分别在梁的跨中和三分点悬挂集中质量块作为试验模型，采用静力加载方式测得其抗弯刚度为32 N·m2，附加质量块m重量为1 kg。试验时光线良好，背景颜色为白色，摄像头视角水平，焦距固定并保持测距不便，以有利于图像中梁的边缘检测。视频采集采用普通数字摄像头，采样帧率为30 fps，分辨率为640像素×480像素，采取在梁上施加一集中力使梁产生一初始位移然后突然卸载的方式进行激振，试验模型见图3。

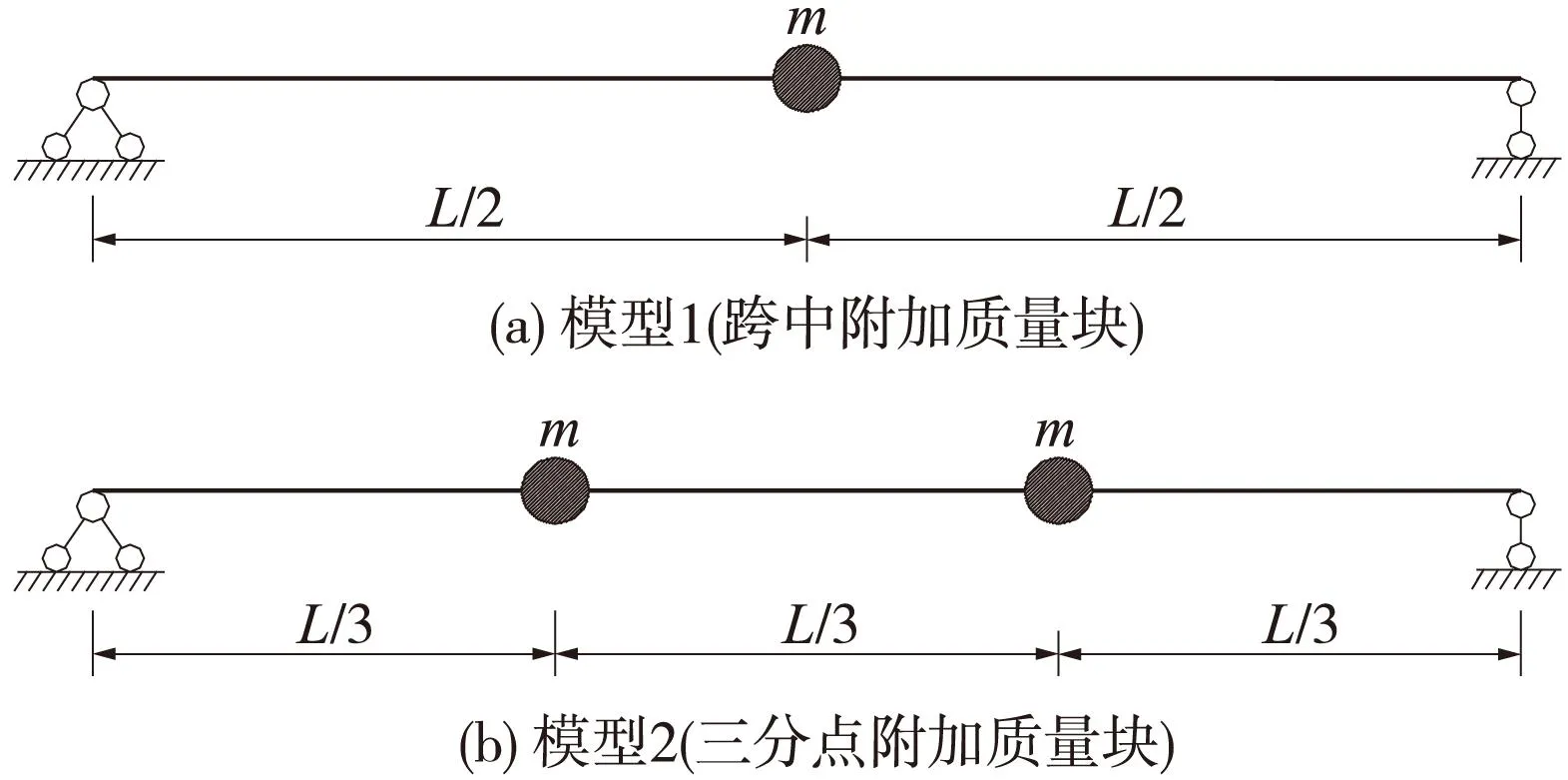
图3　模型简图

图3中简支梁模型的理论一阶固有频率为

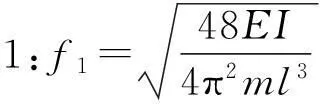
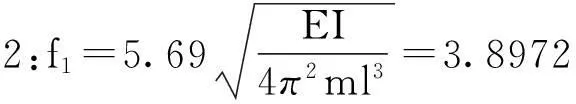
3.2测试步骤

开始振动试验，待简支梁振动稳定后进行视频采集，采集5 s共获取150幅图像。

基于复Morlet小波变换的模态参数识别步骤如下：

(1)由信号的采样频率与信号的长度选定复Morlet小波函数的中心频率fc及频带宽fb，确定小波分析的最大、最小尺度及尺度离散间隔。

(2)对信号进行连续复小波变换，计算各尺度下信号小波系数的模，对同尺度下信号小波系数的模取均值，并确定当模的均值取极值时对应的的尺度。

(3)当尺度ai对应的模的均值取极大值时，提取该尺度下信号小波系数的模与相位，对模的对数及相位用最小二乘法进行直线拟合，由模的半对数直线斜率及相位的直线斜率求固有频率与阻尼比，由各像素点在各尺度下模取极值时的小波系数拟合模态振型。

3.3小波分析识别结果

信号的采样频率fs为30 Hz，采样时间为T=5 s，信号长度L=150，取Morlet母小波函数的中心频率fc=fs=30，考虑边缘效应，带宽参数fb取0.25 Hz，最大尺度amax=l/6=25，最小尺度选定为amin=2。可选取小波函数cmorl30-0.25(fs=30 Hz，fb=0.25 Hz)分析振动信号，图4给出了模型梁320像素点振动信号小波分析的尺度-模图、小波变换模的对数-时间图及小波变换的相位-时间图。识别结果列于表1中，另在表1中给出了FFT的识别结果，其中固有频率与阻尼比分别采用峰值法与对数衰减率法识别。

对有限长的信号进行小波变换时，无论小波的带宽参数变化如何，边缘效应总是无法完全消除的，这里采用对信号边界的对称线性延拓来避免边缘效应。由表1的测试结果可看出，连续小波分析方法与FFT识别的结果接近，较理论值差别不大，固有频率和阻尼比的识别结果均比较稳定，各像素点的小波系数模极大值发生在320像素位置。以该点的小波系数对其余各点进行归一化并拟合进行振型识别，振型拟合结果见图5。可见，参与计算的像素点个数越多，振型分析的精度越高，由17个像素点拟合得出的振型已基本接近理论振型。

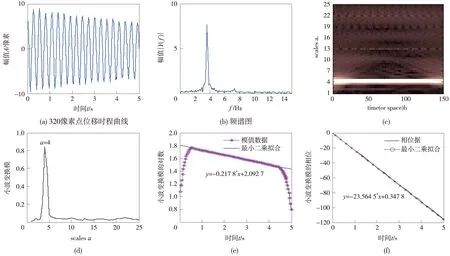
图4　320像素点信号的小波分析结果

图5　拟合不同像素点的振型

3.4试验结果分析

频率结果分析：模型1由DWT实测一阶频率为4.321 5 Hz，由FFT实测一阶频率为4.335 9 Hz；模型2由DWT实测一阶频率为3.741 6 Hz，由FFT实测一阶频率为3.750 0 Hz；二种方法的测试结果基本一致，均小于理论值4.745 2 Hz和3.897 2 Hz，主要原因为理论计算时未考虑梁的质量。

表1　模态参数识别结果

阻尼比结果分析：模型1由小波分析法测得的阻尼比范围为0.612%～0.698%，对数衰减率法测得阻尼比范围为0.590%～0.690%；模型2由小波分析法测得的阻尼比范围为0.901%～0.946%，对数衰减率法测得阻尼比范围为0.911%～1.071%，两种方法测试结果基本一致。具体见表2所示。

表2　两种方法识别结果对比

4结束语

采用数字图像识别技术与小波分析技术，以MATLAB软件平台构建视频图像测振系统，并采用该系统进行简支梁模型的模态试验，得出以下结论：

(1)在合理的安排下，可采用视频图像识别技术实现低频、振幅较大的梁桥动挠度及振动检测；针对桥梁振动检测中利用跳车、跑车激振引起桥梁振幅较明显的检测工况，可采用视频图像方法检测其振动特性。

(2)采用合适的Morlet复小波函数对振动信号进行连续复小波分析，由分析得到的小波系数及其相位和幅角可识别出梁的固有频率、阻尼比和阵型，识别结果与FFT分析结果比较一致。

(3)图像测量为点式或面式检测，可获得结构表面较完备的信息，而小波分析具有多分辨率分析的特点，结合两种技术或可在结构损伤识别方面取得突破，但应重视测试噪声的影响。

参考文献

[1]高山.铁路工程地质遥感调查中的图像解译质量分析[J].铁道勘察，2010(3):24-27

[2]黄昶，林莉.多源遥感影响融合技术在土地动态监测中应用[J].铁道勘察，2011(4):32-36

[3]李岩，方子岩.近景摄影测量中如何选择交向摄影[J].铁道勘察，2012(6):26-29

[4]黄文.数字图像处理技术在梁索结构振动测试中的应用研究[D].广州：广州大学，2014

[5]袁向荣.梁变形检测的一维数字图像相关法[J].广州大学学报，2010，9(1):54-56

[6]袁向荣，刘敏，蔡卡宏.采用数字图像边缘检测法进行梁变形检测及破损识别[J].四川建筑科学研究，2013，39(1):68-70

[7]王翔，钟继卫，王波.桥梁动态挠度图像识别测试技术研究[J].世界桥梁，2015，43(3):59-62

[8]Lardies Joseph，Ta Minh-Nghi. A wavelet-based approach for the identification of damping in non-linear oscillators[J]. Journal of Mechanical Sciences， 2005，47:1262-1281

[9]孙延奎.小波分析及其应用[M].北京:机械工业出版社，2005

[10]Le Thien-Phu， Pierre Argoul. Continuous wavelet transform for modal identification using free decay response[J]. Journal of Sound and Vibration， 2004，277(1-2):73-100

中图分类号：TN911.7； TU311

文献标识码：A

文章编号：1672-7479(2016)01-0011-04

作者简介：第一胡朝辉(1984—)，男，硕士，工程师。

收稿日期：2015-11-27