一种基于坐标系级联的攻角探测方法

2016-04-13朱欣华

中国惯性技术学报 2016年2期

关键词：方位角攻角弹体

徐云，朱欣华，苏岩

（南京理工大学机械工程学院，南京 210094）

一种基于坐标系级联的攻角探测方法

徐云，朱欣华，苏岩

（南京理工大学机械工程学院，南京 210094）

攻角作为描述弹体飞行状态的重要参数，是外弹道测试的重要内容之一。针对制导炮弹空中飞行时直接探测弹丸攻角相对较为困难的问题，提出了一种基于坐标系级联的弹丸攻角探测方法。该方法以弹用MINS/GNSS组合导航参数的输出为基础，建立了弹丸攻角的探测模型，采用坐标系级联的方式实现了弹丸攻角的最优估计。某型精确制导炮弹的数值仿真结果表明：采用本文提出的攻角探测方法得到的攻角估计误差分布在0.7°，并且MINS/GNSS组合导航系统姿态输出精度以及各个传感器测量精度的提高均有助于弹丸攻角的最优估计。该方法是一种在不需要增加额外探测设备的基础上实现弹丸攻角最优估计的有效方法，可以为弹丸攻角探测的实际工程应用提供新思路。

制导炮弹；MINS/GNSS；坐标系级联；攻角探测；最优估计

制导炮弹空中飞行时会受到随机扰动，导致弹轴方向与弹体质心处的速度方向不能保持一致，形成攻角。攻角作为描述弹体飞行状态的重要参数是外弹道测试的重要内容之一。它的存在将会产生与之相应的空气动力和力矩，从而影响弹丸质心的运动[1]。因此，开展弹丸攻角的探测工作对弹体空气动力学、制导炮弹控制系统以及制导方案的设计具有重要的研究意义[2-4]。

由现有文献可以看出，弹体飞行时受到的各种扰动将会使得攻角一直处于高速变化的状态，因此开展弹丸攻角的探测工作较为困难[1]。目前，针对弹丸攻角探测的方法主要可分为直接探测法和间接探测法。直接探测法是利用攻角传感器直接进行测量，该方面的探测理论比较成熟。但是直接探测法仅适用于无人机、遥控飞机以及马赫数小于2.5的非旋转飞行器的攻角测量[5]。对于高速飞行和依靠旋转稳定的制导炮弹而言，直接探测法不适用。间接探测法是通过测量与弹丸攻角相关的参数，实现弹丸攻角的最优估计。国内外常见的方法主要有攻角纸靶测量法、狭缝摄影法，以及基于线阵、面阵CCD的攻角探测法等[6-9]。攻角纸靶测量法通过记录弹丸穿过纸靶时留下的形状、尺寸等参数，推算出弹体飞行时的攻角。该方法探测信息容量小，处理周期时间长，工程实用性较差。狭缝摄影法是通过拍摄弹丸飞过狭缝时弹轴各点留在胶片上的影像从而解算得到弹丸攻角的信息。该方法比较容易实现弹丸攻角高精度的测量值，但需要保证弹体质心运动方向与狭缝垂直，并且弹丸在胶片上的影像速度必须与胶片的运动速度相同。基于线阵、面阵CCD的攻角探测方法是通过线阵、面阵CCD拍摄弹丸经过像机视野的图像，从而重构弹丸形状，计算弹体的飞行速度矢量，并估计出弹丸的攻角。该方法解决了传统胶片式狭缝摄影法需要大量重复更换胶片的问题，但该方法需要应用 CCD等设备，因此增加了系统体积，不利于弹体小型化设计。

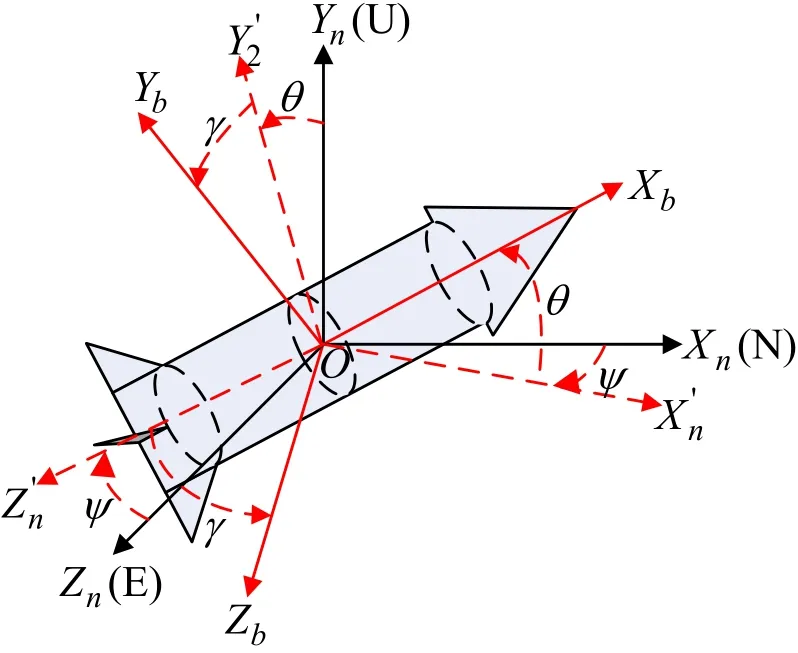
图1 (a) 导航坐标系和弹体坐标系Fig.1(a) Navigation frame and the body frame

采用MINS/GNSS组合导航系统的制导炮弹近年来的报道层出不穷，MINS/GNSS组合导航系统凭借体积小、成本低、短期精度高的优势获得了众多领域的广泛的应用[10-14]。本文针对采用MINS/GNSS组合导航系统的制导炮弹，提出了一种基于坐标系级联的攻角探测方法，利用MINS/GNSS导航参数的输出，实现了飞行中弹丸攻角的探测。与现有文献中报道的方法相比，不需要增加额外探测设备即可实现弹丸攻角的探测，为攻角探测的工程应用提供了一种新思路。

1 攻角探测用坐标体系

本文使用的坐标体系有导航坐标系 OXnYnZn（N系）、弹体坐标系OXbYbZb（B系）、弹道坐标系OX2Y2Z2（V系）、弹轴坐标系Oξηζ（A系）、第二弹轴坐标系Oξη2ζ2（A2系）。

选用北天东坐标系（NUE）作为导航坐标系。

导航坐标系与弹体坐标系的关系如图 1(a)所示，其中θ、γ、ψ分别为俯仰角、滚转角和偏航角，用于表征弹体坐标系和导航坐标系的转动关系。

导航坐标系和弹道坐标系的关系如图1(b)所示，其中θa和ψ2分别为弹道倾角弹道方位角。

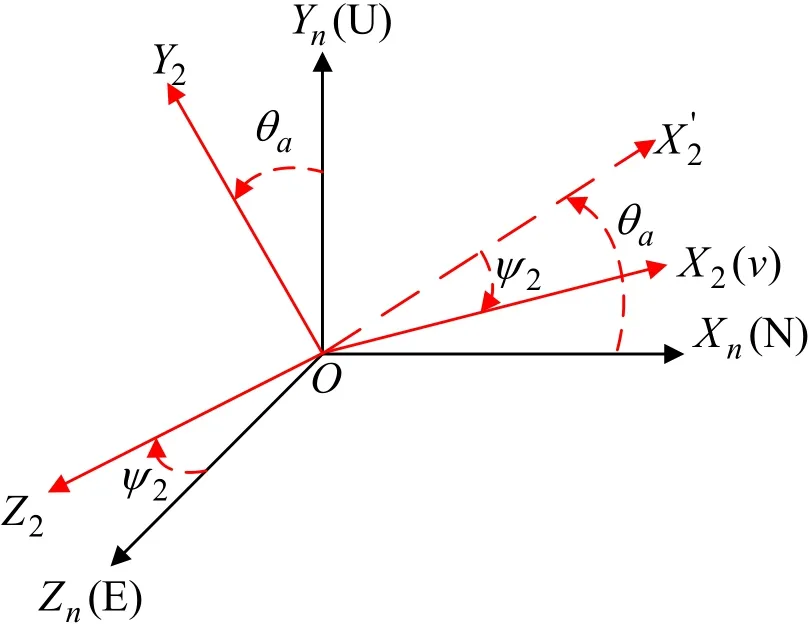
图1 (b) 导航坐标系和弹道坐标系Fig.1(b) Navigation frame and trajectory-axis frame

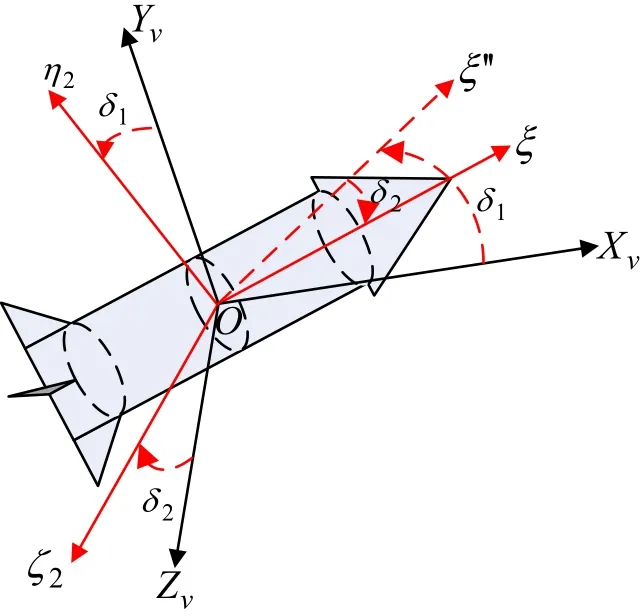
图1 (c) 导航坐标系和弹轴坐标系Fig.1(c) Navigation frame and axis frame

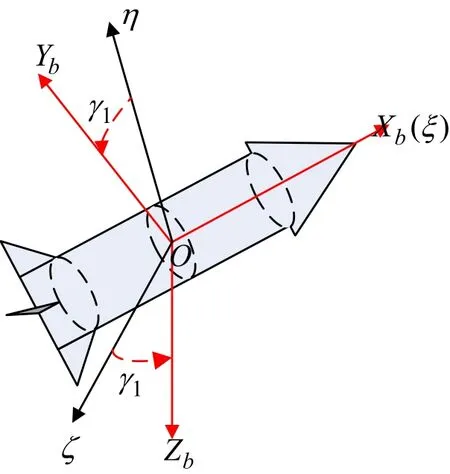
图1 (d) 弹体坐标系与弹轴坐标系Fig.1(d) Body frame and axis frame

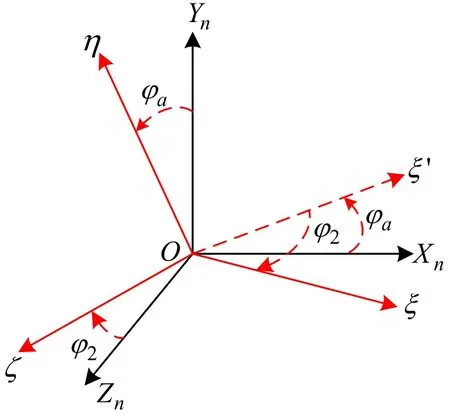
图1 (e) 弹道坐标系与第二弹轴坐标系Fig.1(e) Trajectory-axis frame and 2rd axis frame

弹轴坐标系与导航坐标系的关系如图 1(c)所示，其中 φa和 φ2分别为弹轴高低角弹轴方位角。根据定义，弹轴高低角与弹轴方位角分别等于俯仰角和偏航角，即φa=θ，φ2=ψ。

弹体坐标系与弹轴坐标系的关系如图1(d)所示，其中γ1为弹体坐标系相对于弹轴坐标系转动的角度。

弹道坐标系与第二弹轴坐标系的关系如图 1(e)所示，其中，δ1、δ2分别表示为高低攻角和方位攻角。

弹轴坐标系与第二弹轴坐标系之间相差一个转角β，对于正常飞行的弹体而言，转角β近似为0。

2 基于坐标系级联的攻角探测模型

2.1 基于坐标系级联的攻角探测模型

由第1节的介绍可得各个坐标体系之间的关系如图2所示。

根据图1(a)，采用三个姿态角θ、γ、ψ表征弹体坐标系与导航坐标系之间的关系，有：

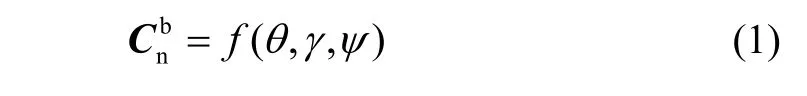
若采用θa、ψ2、γ1、δ1、δ2、β来表征弹体坐标系与导航坐标系之间的关系，则有：

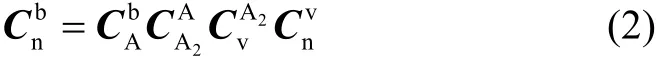
理论上，式(1)与(2)等价。在已知θ、γ、ψ、γ1、β、θa、ψ2的情况下，我们可以将求解弹丸攻角的问题转换为求解坐标矩阵的问题。

根据第1节的介绍，式(1)与式(2)中的坐标转换矩阵可分别表示为

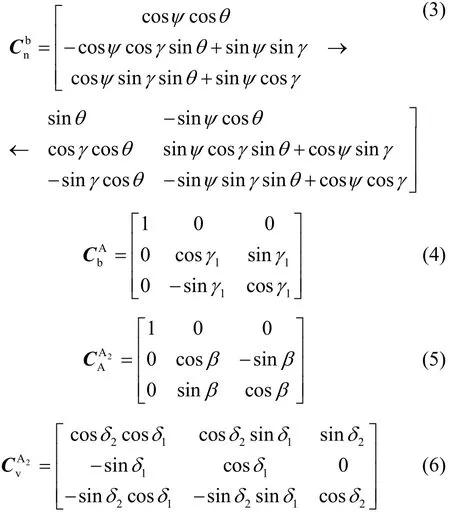
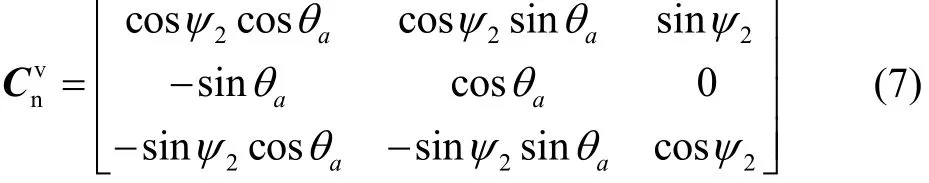
图2 坐标体系转换关系图Fig.2 Coordinate system conversion

2.2 模型参数解算

2.2.1 飞行姿态θ、γ、ψ的解算

制导炮弹在导航坐标系内进行导航解算，得到弹体飞行时的三个姿态角，其误差传播方程为

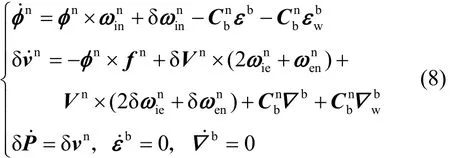
在误差方程(8)的基础上，取15维的Kalman滤波估计的状态量为

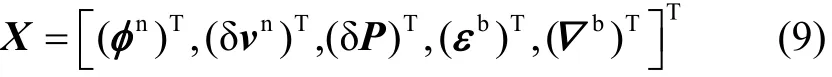
由此可得滤波估计模型的状态方程为

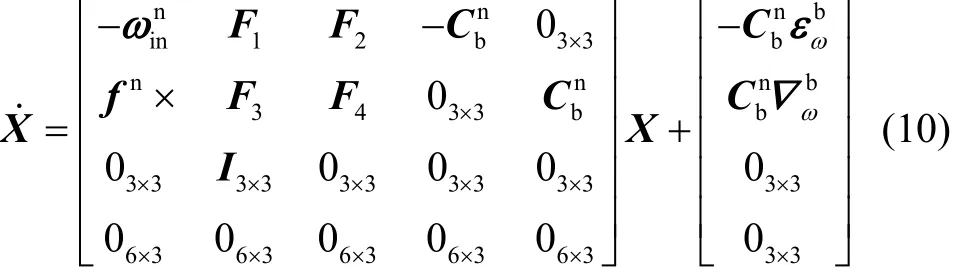
式中，F1、F2、F3、F4详见附录。

设制导炮弹用MINS以及GNSS在惯性系下的速度和位置输出分别表示为VMINS、VGNSS、PMINS、PGNSS，则Kalman滤波模型估计的观测方程定义为

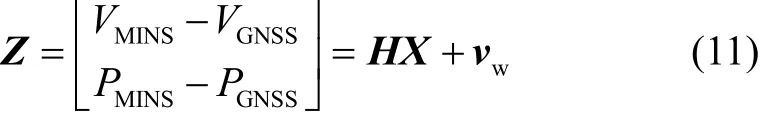
式中：H=[06×3, I6×3, 06×6]，vw为GNSS的测量噪声。

式(10)和式(11)构成了基于“速度+位置”观测的15维 Kalman滤波估计模型，采用该模型对制导炮弹用MINS/GNSS组合导航系统进行姿态估计，从而获得弹体的实时姿态θ、γ、ψ。

2.2.2 自转角γ1的解算

自转角γ1反映了弹体坐标系相对于弹轴坐标系的转动角度。该角度可通过轴向陀螺仪的输出进行解算获得。

式中：

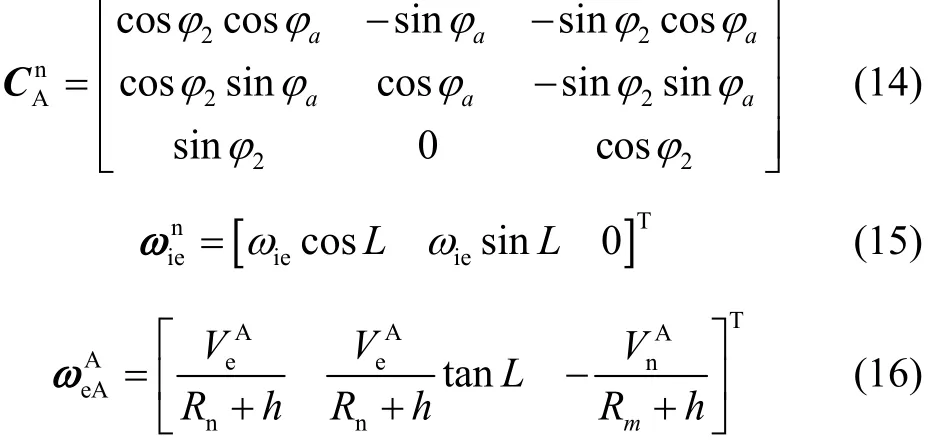
速度矢量在弹轴坐标系与导航坐标系下存在如下关系：

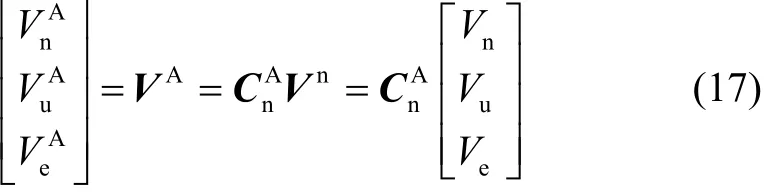
因此，自转角γ1可按下式计算：

2.2.3 转角β的解算

根据第1节可知，对于正常飞行的弹体而言，转角β近似为0，因此矩阵可近似为单位矩阵。

2.2.4 弹道方位角θa、弹道倾角ψ2的解算

弹道方位角 θa和弹道倾角 ψ2的计算可以通过弹载GNSS设备以及MINS中加速度计的测量输出解算获得。针对MINS安装在弹体质心处以及非质心处分别对弹道方位角和弹道倾角的解算进行讨论。

1）MINS安装在弹体的质心位置，则

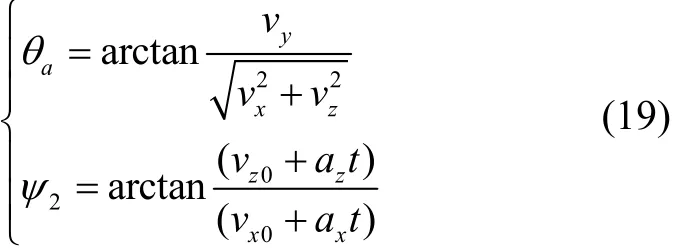
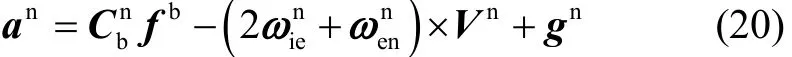
2）MINS安装在弹体非质心位置，如图3所示。

设MINS的x轴向与弹体纵轴重合，且MINS的安装位置与弹体质心处的偏心距为(dx, dy, dz)。分别对y轴向和z轴向的比力进行补偿，有：

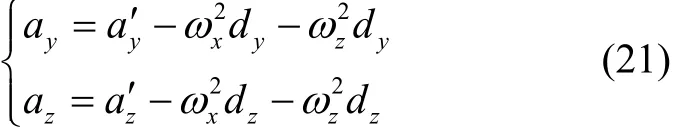
式中：ay′和az′分别为导航坐标系下y轴和z轴的比力；ωz分别为导航坐标系下y轴与z轴的角速度。将式(22)代入式(20)即可得到MINS在非质心位置安装方式下的弹道方位角θa、弹道倾角ψ2的解。

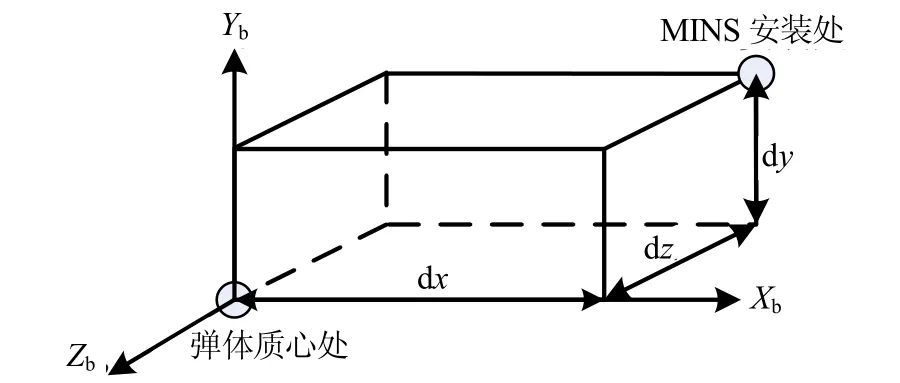
图3 MINS安装在非质心处的示意图Fig.3 Non center installation of MINS

3 仿真验证和误差分析

3.1 仿真验证

本文以某型制导炮弹为研究对象，弹径为 120 mm，弹重17.256 kg。初始速度为420 m/s，初始射角为45°，初始自转速为3.23 rad/s。根据六自由度外弹道方程[1]获得飞行过程中弹体的全弹道参数。

算例仿真中基于上述全弹道参数生成MINS以及GNSS的模拟测量输出。其中，三个轴向陀螺仪的输出是通过在弹体坐标系各轴上的角速度(ωx, ωy, ωz)添加相应的误差获得（针对目前 MEMS陀螺的性能现状，角速度测量误差均值为10 (°)/h，标准偏差为5 (°)/h的高斯白噪声，更新率为 100 Hz），三个轴向加速度的输出通过在弹体坐标系各轴上的加速度(ax, ay, az)添加相应的误差获得（针对目前MEMS加速度计的性能现状，加速度测量误差均值为1 mg，标准偏差为1 mg的高斯白噪声，更新率为100 Hz），GNSS的速度输出通过在弹体质心处的速度方向添加三个标准偏差为0.1 m/s的高斯白噪声获得，位置输出通过在弹体质心处的位置添加经纬度标准偏差为0.001°的高斯白噪声和高度标准偏差为2 m的高斯白噪声获得。

采用本文提出的攻角探测模型，得到高低攻角、方位攻角的估计误差曲线如图4所示。

从图4可以看出，采用本文提出的攻角探测方法得到的攻角估计误差大致分布在±0.7°以内。

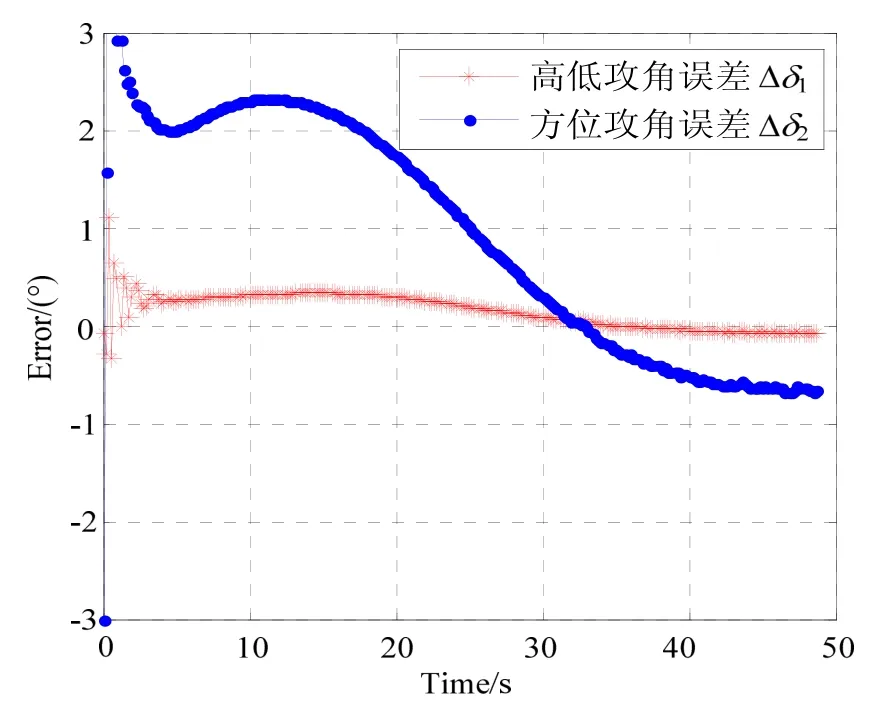
图4 攻角估计误差曲线Fig.4 Estimation errors of the attack angles

3.2 误差分析

从本文提出的基于坐标系级联的攻角探测模型可以看出，攻角的探测误差源主要包括：姿态角θ、γ、ψ估计误差，转动角γ1的解算误差，转角β的解算误差，弹道方位角 θa与弹道倾角 ψ2的解算误差。下面依次分析这些误差对攻角探测精度的影响。

① 姿态角θ、γ、ψ的估计误差

假设其余误差源为零，仅存在姿态角θ、γ、ψ的估计误差，此时选用航向跟踪模式提高姿态角的估计精度，得到的攻角估计误差曲线如图5所示。

由图5可以看出，不考虑其他误差源的前提下，采用航向跟踪提高姿态角的估计精度后，攻角估计误差能够有效地减小，使得高低攻角和方位攻角的估计误差均分布在±0.025°范围内。

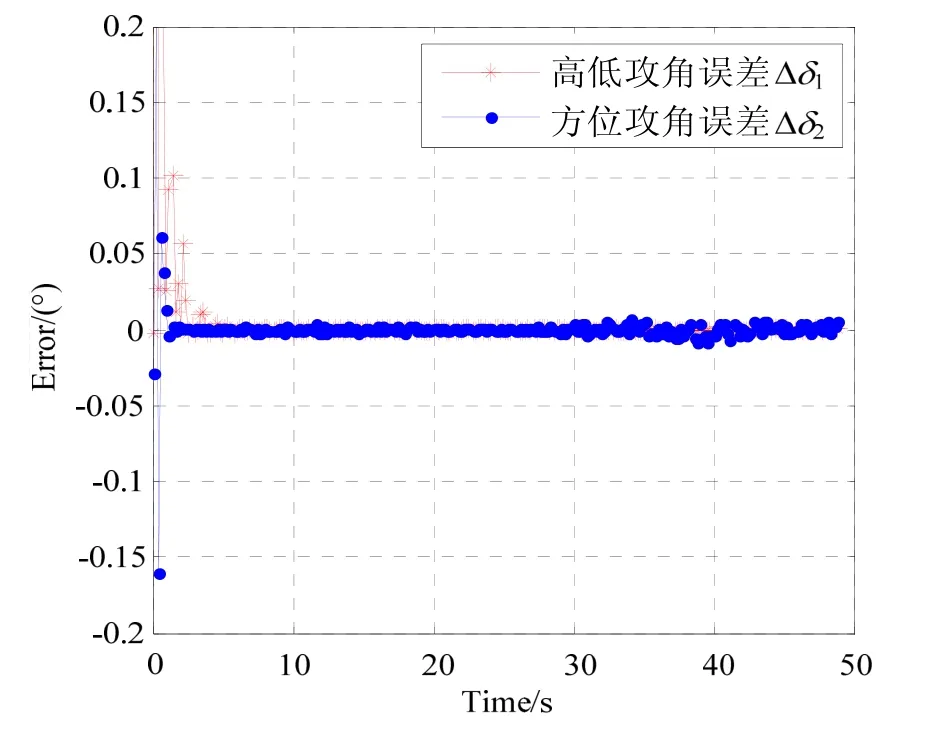
图5 航向跟踪时，攻角估计误差曲线Fig.5 Estimation errors of the attack angles for course tracking

假设其余误差源为零，仅存在转动角γ1的解算误差，得到攻角估计误差曲线如图6所示。

由图6可以看出，仅存在转动角解算误差时，高低攻角和方位攻角的估计误差均分布在±5E-3°范围内。

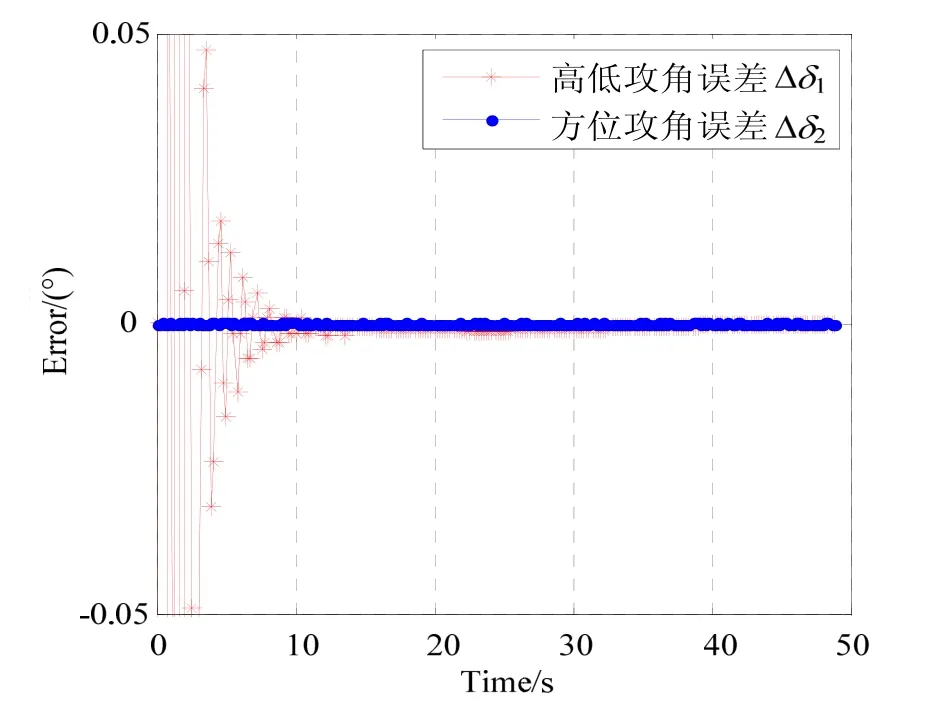
图6 仅存在γ1误差时，攻角误差估计曲线Fig.6 Estimation errors of the attack angles for the error ofγ1

根据弹轴坐标系和弹体坐标系的关系，采用轴向陀螺仪的测量输出直接积分来近似估计转动角γ1，此时攻角解算误差的如图7所示。

比较图6可以看出，图7中攻角误差估计曲线比图7中的攻角误差估计的速度较快，尤其是针对起始段的攻角估计误差。同时，图7表明采用轴向陀螺仪的测量输出直接近似估计转动角γ1，此时攻角解算误差同样分布在±5E-3°范围内。与图6中的攻角误差估计精度相当。

这说明，采用轴向陀螺仪的测量输出直接近似估计转动角γ1，从而进行攻角估计能够满足攻角估计精度的要求。对于工程应用而言，该近似方法适用。

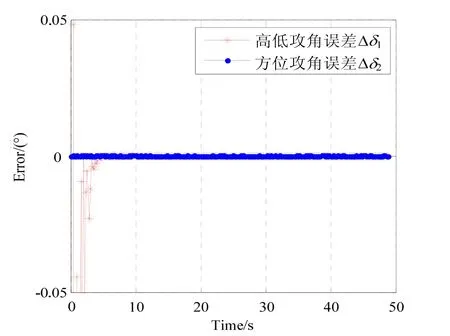
图7 仅存在γ1误差时，攻角误差估计曲线Fig.7 Estimation errors of the attack angles for the error of γ1

由于本文建立的攻角探测模型中将转角β近似为零处理，为验证模型的准确性，设其他误差源均为0，此时姿态角、转动角、弹道方位角、弹道倾角均采用理论值代替，得到的攻角误差估计曲线如图8所示。

由图8可以看出，将转角β近似为零处理时得到的攻角探测误差分布在±5E-14°的数量级，证明了本文提出的攻角探测模型在理论上是可行的。④ 弹道方位角θa与弹道倾角ψ2的解算误差

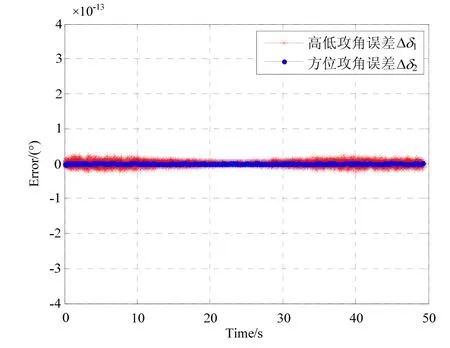
图8 无误差源时，攻角估计误差曲线Fig 8 Estimation errors of attack angles without error sources

假设仅存在弹道方位角、弹道倾角的解算误差，此时得到的攻角估计误差曲线如图9所示。

由图9可以看出，弹道方位角与弹道倾角的解算误差使得攻角探测误差分布在±0.02°范围内。从第 2节可知，弹道方位角和弹道倾角的解算精度取决于组合导航系统中加速度计以及GNSS的测量精度。

由误差分析可以看出：转动角γ1的解算误差以及转角β对于攻角探测精度的影响较小；姿态角θ、γ、ψ测量精度的提高以及弹道方位角 θa与弹道倾角 ψ2测量精度的提高对攻角探测精度的提高影响较大。

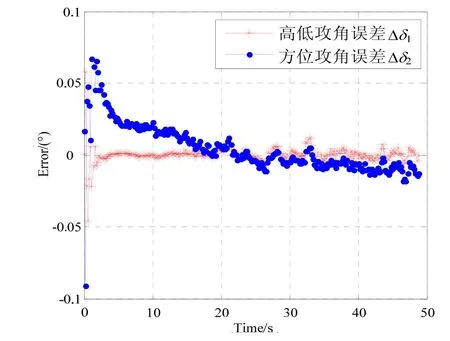
图9 仅存在θa与ψ2的误差时，攻角误差估计曲线Fig.9 Estimation errors of attack angles for error of θaand ψ2

4 结论

本文以采用MINS/GNSS组合制导的精确制导炮弹为研究对象，提出了基于坐标系级联的攻角探测模型，并给出了攻角探测模型中各类参数的解算过程。采用某型精确制导炮弹的全弹道数据进行数值仿真，结果表明本文提出的攻角探测误差分布在±0.7°范围以内。误差分析表明：转动角的解算误差对于攻角探测误差的影响较小；姿态角的估计精度以及弹道方位角和弹道倾角测量精度的提高能够有效地减小攻角探测误差，为基于该方案的攻角探测技术的进一步研究指明了方向。

（References）：

[1] 韩子鹏. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2008.

[2] Bhagwandin V A, Sahu J. Numerical prediction of pitch damping stability derivatives for finned projectiles[J]. Journal of Spacecraft and Rockets, 2014, 51(5): 1603-1618.

[3] Fresconi F, Celmins I, Ilg M, et al. Projectile roll dynamics and control with a low-cost maneuver system[J]. Journal of Spacecraft and Rockets, 2014, 51(2): 624-627.

[4] Putnam Z R, Grant M J, Kelly J R, et al. Feasibility of guided entry for a crewed lifting body without angle-ofattack control[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 729-740.

[5] 杨翔, 王雨时, 闻泉. 迫击炮弹空气动力特性攻角系数数值研究[J]. 弹箭与制导学报, 2014, 34(2): 139-141. Yang Xiang, Wang Yu-shi, Wen Quan. Numerical simulation on aerodynamic characteristics about angle of attack coefficient of mortar projectiles[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(2): 139-141.

[6] Zhao Z, Wen G. Ball’s motion estimation using a line-scan camera[J]. Measurement Science Review, 2011, 11(6): 185-191.

[7] Yayla S, Canpolat C, Sahin B, et al. The effect of angle of attack on the flow structure over the nonslender lambda wing[J]. Aerospace Science and Technology, 2013, 28(1): 417-430.

[8] Soria J, New T H, Lim T T, et al. Multigrid CCDPIV measurements of accelerated flow past an airfoil at an angle of attack of 30[J]. Experimental thermal and fluid science, 2003, 27(5): 667-676.

[9] Ishii H, Molinari A P, Leech N A, et al. Method and apparatus for determining an angle of attack from multiple ball hitting. US Patent 8 974 313[P]. 2015-3-10.

[10] 孔星炜, 郭美凤, 马芮, 等. 一种制导炸弹 MINS/GPS导航系统误差分析与分配[J]. 中国惯性技术学报, 2009, 17(1): 37-41. Kong Xing-wei, Guo Mei-feng, Ma Rui, et al. Errors analysis and allocation of MINS/GPS system in guided bomb[J]. Journal of Chinese Inertial Technology, 2009, 17(1): 37-41.

[11] Wu Y, Wang J, Hu D. A new technique for INS/GNSS attitude and parameter estimation using online optimization[J]. IEEE Transactions on Signal Processing, 2014, 62(10): 2642-2655.

[12] 张金亮, 秦永元, 梅春波. 基于 MEMS 惯性技术的鞋式个人导航系统[J]. 中国惯性技术学报, 2011, 19(3): 253-256. Zhang Jin-liang, Qin Yong-yuan, Mei Chun-bo. Shoemounted personal navigation system based on MEMS inertial technology[J]. Journal of Chinese Inertial Technology, 2011, 19(3): 253-256.

[13] Chu H J, Tsai G J, Chiang K W, et al. GPS/MEMS INS data fusion and map matching in urban areas[J]. Sensors, 2013, 13(9): 11280-11288.

[14] Mei C B, Qin Y Y, You J C. SINS in-flight alignment algorithm based on GPS for guided artillery shell[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 51-57.

附录

Attack-angle detection method based on cascaded coordinate systems

XU Yun, ZHU Xin-hua, SU Yan

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

The attack angle of a guided projectile can describe the projectile’s flight attitude, so it is one of the most important testing parameters during exterior ballistic experiments. In view that the guided projectile in flight is difficult to directly detect the attack angle, a new method for attack-angle estimation is proposed based on a coordinate cascade. According to the navigation parameters obtained by MINS/GNSS, the detection model for the attack angle is established, and then the estimation of the attack angle is realized by the coordinate cascade. The simulation is made based on the trajectory data of a precision guided projectile, which show that the estimation error of the attack angle is within 0.7°. The error analysis indicates that the high accuracy of the attitude estimation and the outputs by the sensors from MINS/GNSS are helpful to improve the estimation accuracy of the attack angle. The proposed method is effective to realize the detection of the attack angle for the guided projectile without any additional equipment, thus it provides a new idea for the practical detection of the attack angle.

guided projectile; MINS/GNSS; cascaded coordinate systems; attack-angle detection; optimal estimation