基于自适应无迹粒子滤波的SINS大方位失准角初始对准

2016-04-13徐晓苏刘义亭张利斌

中国惯性技术学报 2016年2期

孙进，徐晓苏，刘义亭，张利斌

（1. 东南大学仪器科学与工程学院微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 常州信息职业技术学院电子与电气工程学院，常州 213164）

孙进1，徐晓苏1，刘义亭1，张利斌2

针对捷联惯导系统大方位失准的情况进行分析，提出了采用了自适应UPF滤波进行初始对准的方法。该滤波器基于强跟踪滤波器的思想，通过引入衰减记忆因子有效增强当前信息残差对系统的修正作用，在一定程度上降低了由于系统简化、噪声统计特性不确定对系统造成的影响，同时较好地克服了UPF中粒子退化的现象。当系统噪声统计特性确定时，自适应UPF水平对准时间比UPF对准时间大约少200 s，方位对准时间大约少150 s，对准结束后，自适应UPF对准的纵摇、横摇以及航向误差均值分别为-0.018°、0.0074°、-0.8609°，UPF对准对应的值分别为0.0209°、0.0189°、1.0983°。当系统噪声统计特性不确定时，自适应UPF水平对准时间比UPF对准时间大约少400 s，方位对准时间大约少450 s，对准结束后，自适应UPF对准的纵摇、横摇以及航向误差均值分别为0.0105°、0.0122°、-0.7304°，UPF对准对应的值分别为0.0454°、0.0278°、2.8174°。仿真结果表明：在系统噪声统计特性确定或不确定的情况下，自适应UPF能在一定程度上提高大方位失准捷联惯导系统的初始对准速度和对准精度。

捷联惯导系统；大失准角；初始对准；无迹粒子滤波；自适应无迹粒子滤波

初始对准是捷联惯导系统中的关键技术之一，其对准时间和精度直接影响惯导系统的工作性能[1]。

随着导航系统应用领域的不断拓展，大多数应用环境不能满足初始失准角为大角度和噪声为高斯白噪声的条件，此时继续使用传统导航系统线性化模型和卡尔曼滤波（Kalman Filter，KF）将会产生较大的模型误差和估计误差，使得导航参数不可信[1]。针对这种情况，国内外的研究主要分为两个方面：一是惯性导航系统的非线性模型的研究[2-6]。由于捷联惯性导航系统的严格数学误差模型是一组非线性微分方程，以线性模型去逼近非线性模型，必然存在一定的建模误差。小失准角线性模型只有在假设各种误差源较小的条件下才成立，而实际中粗对准的失准角在很多情况下为大角度，因此直接采用非线性模型更能真实地反映误差传播特性。二是非线性滤波器的研究[7-10]，常用的非线性滤波方法有扩展卡尔曼滤波（Extended Kalman Filter，EKF）、无迹卡尔曼滤波（Unscented Kalman Filter，UKF）、粒子滤波（Particle Filter，PF）、EKF-PF、UKF-PF（UPF），在一定程度上UPF的使用限制更少，滤波效果要优于其他几种。本文针对UPF的不足进行改进，基于强跟踪滤波器的思想对UPF进行改进使 UPF具有一定的自适应能力，并将自适应UPF应用于捷联惯性导航系统（Strapdown Inertial Navigation System，SINS）大方位失准的初始对准中，通过引入衰减记忆因子有效增强当前信息残差对系统修正作用，在一定程度上降低了由于系统简化、噪声统计特性不确定对系统造成的影响，同时较好地克服了UPF中粒子退化的现象。将UPF和自适应UPF两种非线性滤波器在初始对准中的滤波效果进行了比较，结果表明自适应UPF比UPF具有更快的收敛速度并且在一定程度上提高对准精度。

1 SINS非线性误差模型

对于捷联系统大失准角情况，转动次序引起的误差无法忽略，必须针对大失准的情况重新建立 SINS的误差模型。使用欧拉平台误差角来表示理想导航坐标系与计算导航坐标系之间的失准角，且该组误差角需要考虑转动的先后顺序。建立相应的 SINS非线性误差模型。

本文坐标系选取如下：

i系——地心惯性坐标系；

e系——选取“东-北-天（E-N-U）”地球坐标系；

n系——选取地理坐标系为导航坐标系；

b系——“右-前-上”坐标系为捷联惯导坐标系。

n系先后依次经过三次欧拉角转动至b系，这三个欧拉角分别记为航向角俯仰角和横滚角系与b系之间的旋转变换关系可用姿态矩阵描述[6]。

1.1 姿态误差方程

实际工作的导航系统由于存在各种干扰和量测误差，SINS的计算平台坐标系(n′系)通常与理想导航坐标系(n系)之间存在转动误差。n系需按照一定的顺序依次转过三个角度才能与n′系重合，现假设这三次转动依次绕z轴、x轴、y轴旋转，且转过的角度分别记为φz、φx、φy，其矢量表示形式为三次旋转对应的姿态变换阵依次为Czφ、Cxφ、Cyφ，故n系至n′系的变换矩阵为

由文献[6]可以得到SINS姿态误差方程为

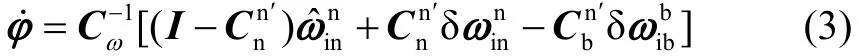
1.2 速度误差方程

在导航坐标系中，SINS速度微分方程[6]为

但在实际系统中该速度微分方程含有误差，此时SINS速度微分方程应为

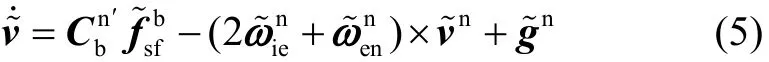
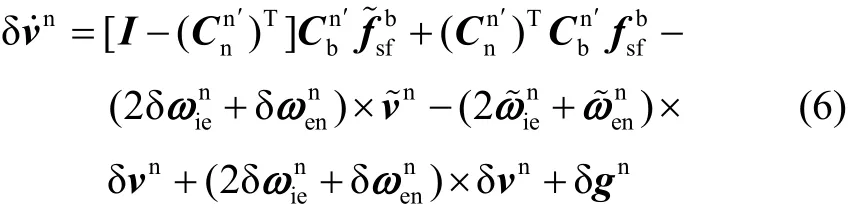
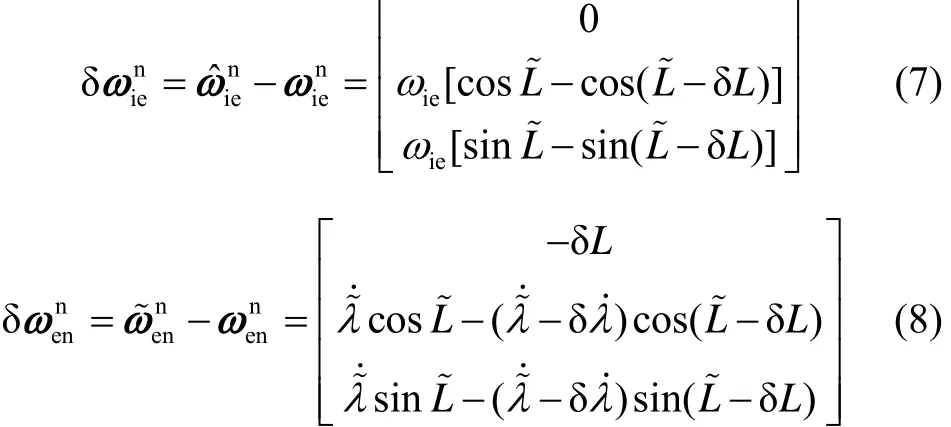
1.3 SINS大方位失准角初始对准误差模型

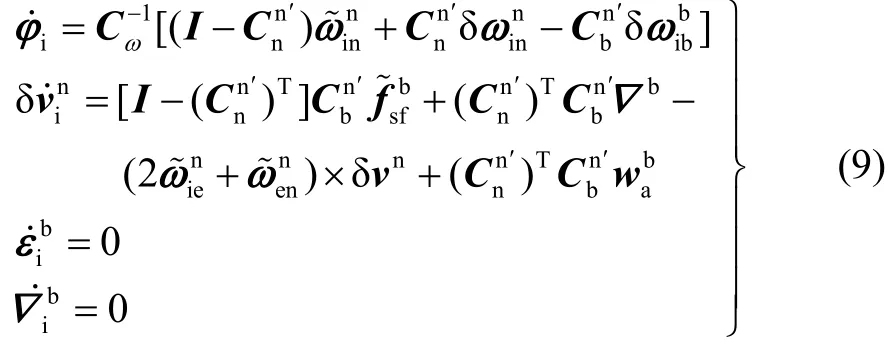
状态向量取

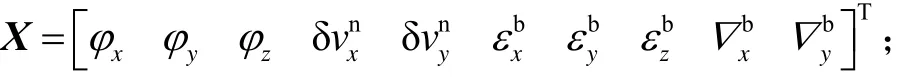
噪声向量取

2 UPF和自适应UPF

2.1 UPF算法

1）初始化：k=0。从初始的前验概率分布p(x0)中进行N个粒子的采样，即

2）加权粒子的预测、采样：k = 1, 2, …。利用无迹粒子滤波对粒子进行预测更新并计算 Sigma点，

时间更新为

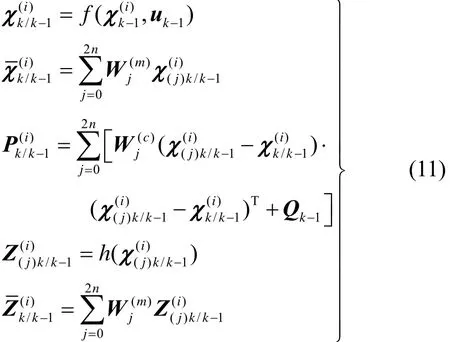
量测更新为

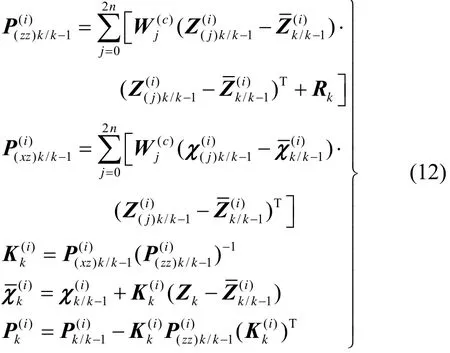
3）根据权值更新公式

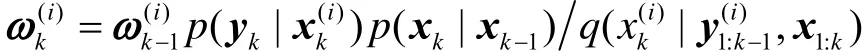
对N个粒子相应的权值进行计算并做归一化处理。

2.2 本文自适应UPF算法

基于强跟踪滤波的的思想，采用时变渐消因子削弱陈旧数据对当前滤波值得影响，实时调整状态预测误差的协方差以及相应的增益矩阵来达到。这在一定程度上能够减缓UPF粒子退化的现象，并且加快粒子滤波的收敛速度。

本文采取的自适应措施是对滤波器的协方差进行判断，具体判断公式如下[10]：式中：S为设定的调整系数，一般取为系统的残差序列

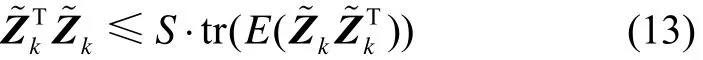
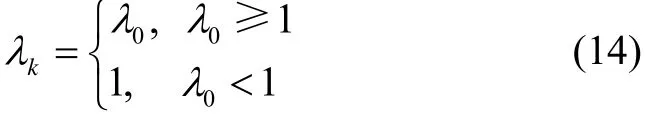
修正公式为

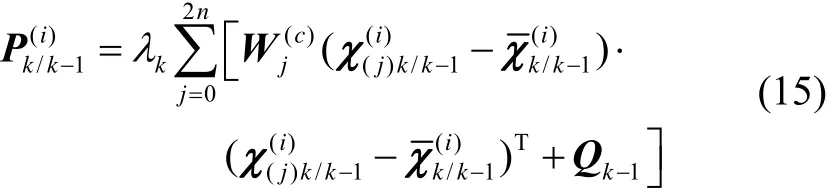
式中，

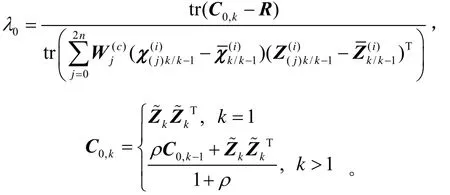
本文自适应UPF的实现步骤如下：

1）初始化：k=0。从初始的前验概率分布p(x0)中进行N个粒子的采样，即

2）预测更新

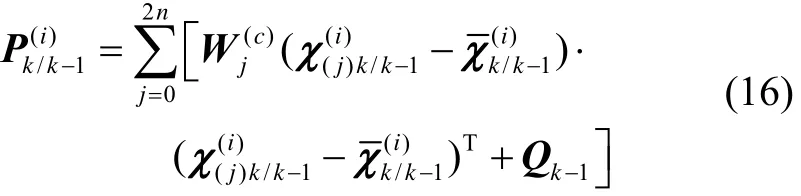
3）判断式(13)是否成立，如果成立则跳至步骤5，否则按照式(15)对进行修正；

4）量测更新

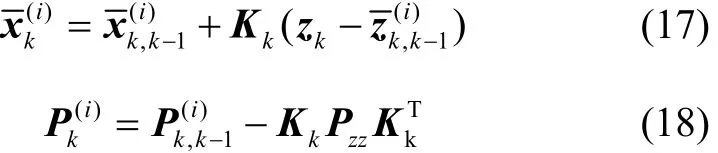
5）根据权值更新公式

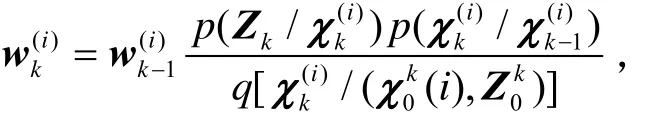
对N个粒子相应的权值进行计算并做归一化处理。

6）通过重采样算法计算重采样的粒子及其权值，

3 UPF滤波影响因素分析——重要性概率密度函数对UPF精度的影响

重要性概率密度函数的选择集中体现在粒子的权重更新部分，即[10]

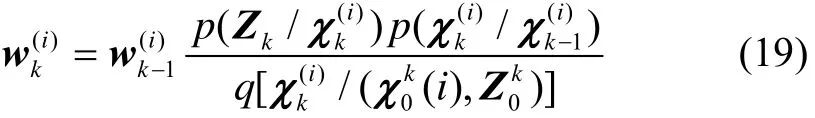
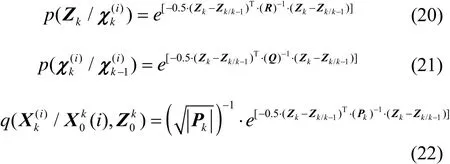
4 仿真及分析

4.1 仿真条件

在静基座条件下：陀螺仪的常值漂移为0.01 (°)/h，随机漂移为；加速度计零偏为100 µg (g = 9.8 m2/s)，随机偏差为50 µg；当地地理纬度为32.37°，经度为118.22°，仿真时间为2000 s。

4.2 仿真结果与分析

1）实验1

按照建立的方位大失准角误差模型，在噪声统计特性确定的情况下分别采用两种滤波算法进行了仿真实验。现选取初始失准角在使用两种滤波算法的情况下。仿真过程中不进行反馈修正，对准误差的仿真结果如图1、图2所示。

图1 大方位失准角对准误差Fig.1 Alignment errors of large azimuth misalignment angles

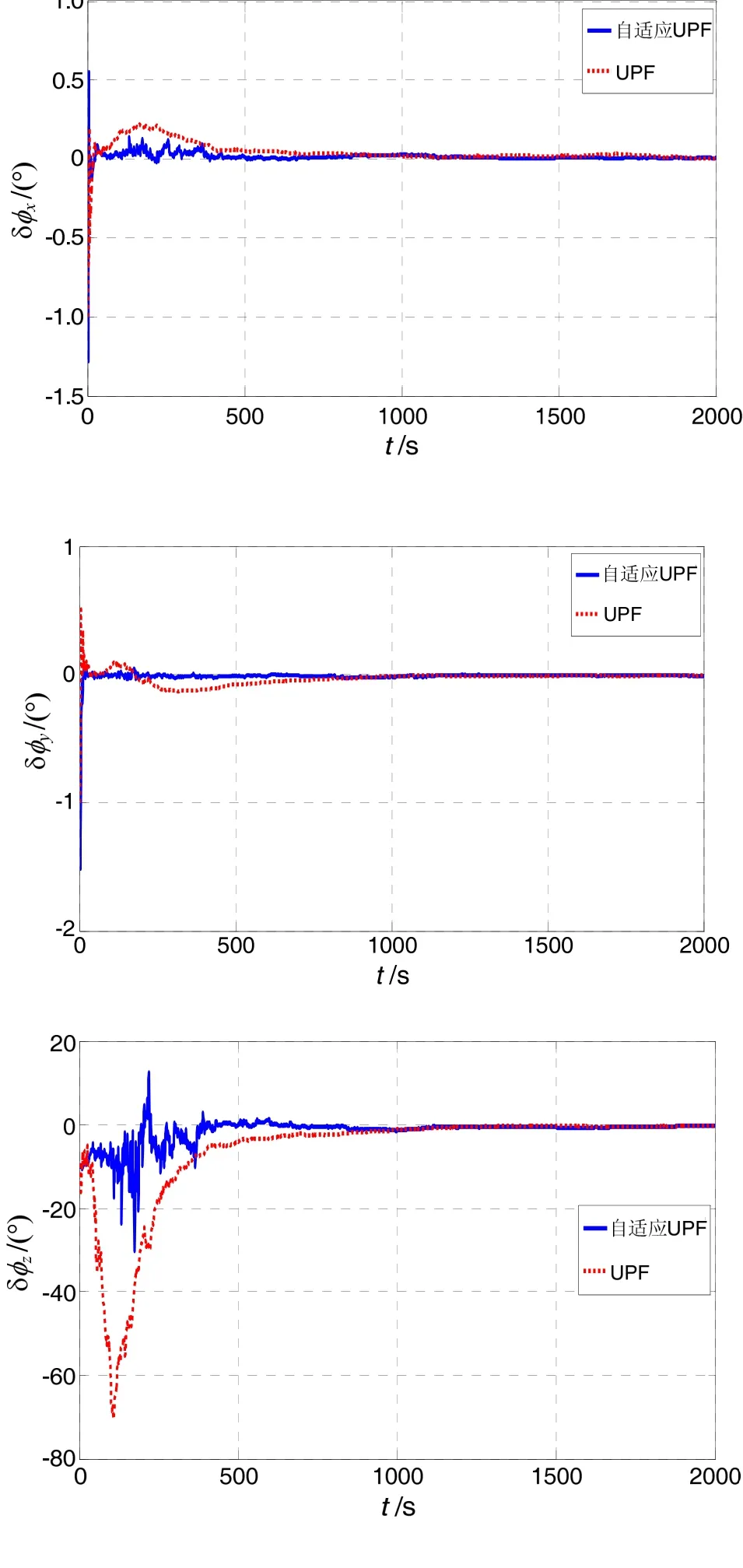
图2 大失准角对准误差Fig.2 Alignment errors of large misalignments angles

表1 确定性噪声下滤波性能对比Tab.1 Comparison on filtering performances when with deterministic noise

表2 不确定性噪声下滤波性能对比Tab.2 Comparison on filtering performances when with uncertain noise

通过图 1 可以看出，基于大方位失准角的 SINS误差模型，当初始失准角为时，采用自适应UPF，水平对准所需时间小于200 s，方为对准所需时间小于450 s。采用UPF，水平对准所需时间约为400 s，方位对准约为600 s。自适应UPF的对准时间明显优于UPF，但两者的对准精度相当。通过表1的统计结果可以看出，在一定程度上采用自适应UPF比UPF的对准精度更高。

2）实验二

为了验证两种滤波方法在具有不确定噪声情况下时的滤波性能，特意在三个方向的加速度上增加了均值为 0.02，方差为 0.02的噪声，进行实验分析。取

通过图 2可以看出，当增加观测噪声后，采用UPF，水平方向上的对准会有一个大幅度的震荡，对系统可能造成一定的影响。水平对准时间大约600 s，方位对准时间大约900 s。采用自适应UPF后，水平对准时间明显优于UPF，约200 s，且误差曲线平滑。方位对准需要450 s，对准时间明显优于UPF。通过表2的统计结果表明，采用自适应UPF的对准精度明显优于UPF。

5 结论

本文通过仿真比较了UPF和自适应UPF在捷联惯导系统大方位失准情况下噪声统计特性固定及噪声统计特性不固定的初始对准，在噪声统计特性确定时使用自适应UPF比普通UPF具有更快的对准速度，对准精度优势不明显。当系统噪声的统计特性不确定时，采用自适应UPF与普通UPF相比，对准速度和对准精度具有明显的优势。

（References）：

[1] 孙枫, 唐李军. 基于CKF的SINS大方位失准角初始对准技术[J]. 仪器仪表学报, 2012, 33(2): 327-335. Sun Feng, Tang Li-jun. Initial alignment of large azimuth misalignment angle in SINS based on CKF[J]. Chinese Journal of Scientific Instrument, 2012, 33(2): 327-335.

[2] Dini D H, Mandic D P, Julier S J. A widely linear complex unscented Kalman filter[J]. IEEE Signal Processing Letters, 2011, 18(11): 623-626.

[3] Donovan G T. Position error correction for an autonomous underwater vehicle inertial navigation system (INS) using a particle filter[J]. IEEE Journal of Oceanic Engineering, 2012, 37(3): 431-445.

[4] Rigatos G G. Nonlinear Kalman filters and particle filters for integrated navigation of unmanned aerial vehicles[J]. Robotics and Autonomous Systems, 2012, 60(7): 978-995.

[5] 薛丽, 高社生, 赵岩. 权值自适应调整 Unscented 粒子滤波及其在组合导航中的应用 [J]. 中国惯性技术学报, 2012, 20(4): 459-463. Xue Li, Gao She-sheng, Zhao Yan. Unscented particle filtering with adaptive adjusted weight and its application in integrated navigation[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 459-463.

[6] 严恭敏, 严卫生, 徐德民. 简化UKF滤波在SINS大失准角初始对准中的应用[J]. 中国惯性技术学报, 2008, 16(3): 253-264. Yan Gong-min, Yan Wei-sheng, Xu De-min. Application of simplified UKF in SINS initial alignment for large misalignment angles[J]. Journal of Chinese Inertial Technology, 2008, 16(3): 253-264.

[7] Gustafsson F, Hendeby G. Some relations between extended and unscented Kalman filters[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 545-555.

[8] Vaccarella A, De Momi E, Enquobahrie A, et al. Unscented Kalman filter based sensor fusion for robust optical and electromagnetic tracking in surgical navigation[J]. IEEE Transactions on Instrumentation and Measurement, 2013, 62(7): 2067-2081.

[9] Zhou J, Yang Y, Zhang J, et al. Applying quaternionbased unscented particle filter on INS/GPS with field experiments [C]//Proceedings of the ION GNSS. Portland, 2011: 1-14.

[10] 李昱辰, 李战明. 噪声未知情况下的自适应无迹粒子滤波算法[J]. 吉林大学学报(工学版), 2013, 43(4): 1439-1445. Li Yu-chen, Li Zhan-ming. Adaptive unscented particle algorithm under unknown noise[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(4): 1439-1445.

Initial alignment of large azimuth misalignment in SINS based on adaptive unscented particle filter

SUN Jin1, XU Xiao-su1, LIU Yi-ting1, ZHANG Li-bin2

(1. Key Laboratory of Micro-inertial Instrument and Advanced Navigation Technology of Ministry of Education, School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China; 2. School of Electronic and Electrical Engineering, Changzhou College of Information Technology, Changzhou 213164, China)

An initial alignment method for Strapdown inertial navigation system (SINS) when with large azimuth misalignment angle is proposed based on an adaptive unscented particle filter (UPF). Inspired by strong tracking filter, a memory attenuation factor is introduced in this adaptive UPF to effectively correct the system by the current information residual. This adaptive UPF can help reduce the influence of the simplified model and the uncertain statistical properties’ noise on the system. Meanwhile, this filter could retard the particle degenerating which often occurs in the particle filter. When the statistics of the system noise is certain, the level alignment time of adaptive UPF is about 200 s less than that of UPF, the azimuth alignment time is about 150 s less; while after the alignment, the pitching, rolling and heading error mean of the adaptive UPF are -0.018°, 0.0074° and -0.8609° respectively, and the corresponding values of UPF are 0.0209°, 0.0189° and 1.0983° respectively. When the statistics of the system noise is uncertain, the level alignment time of adaptive UPF is about 400 s less than that of UPF, the azimuth alignment time is about 450 s less; while after the alignment, the pitching, rolling and heading error mean of the adaptive UPF are 0.0105°, 0.0122° and -0.7304° respectively, and the corresponding values of UPF are 0.0454°, 0.0278° and 2.8174° respectively. Simulation results show that the adaptive UPF can improvethe alignment accuracy and speed of the SINS, no matter the statistical properties of the noise be sure or not.

strapdown inertial navigation system; large misalignment angle; initial alignment; unscented particle filter; adaptive UPF

U666.1

1005-6734(2016)02-0154-06

10.13695/j.cnki.12-1222/o3.2016.02.003

2015-12-28；

2016-03-17

国家自然科学基金项目（61473085，51175082，51375088，61273056）

孙进（1988—），男，博士研究生，从事组合导航研究。E-mail: sunjin8607986@126.com

联系人：徐晓苏（1961—），男，教授，博士生导师。E-mail: xxs@seu.edu.cn