立方星剩磁在轨辨识与主动补偿技术
2016-04-13王群仰
李 烨,郁 丰,王群仰
(1. 航天恒星科技有限公司,北京 100086;2. 南京航空航天大学 航天学院,南京 210016)
立方星剩磁在轨辨识与主动补偿技术
李 烨1,郁 丰2,王群仰1
(1. 航天恒星科技有限公司,北京 100086;2. 南京航空航天大学 航天学院,南京 210016)
立方星的姿态测量与控制系统常采用磁测磁控结合偏置动量轮的方案,整星剩磁干扰力矩是影响姿态控制精度的重要因素之一。提出了一种利用磁强计实现剩磁矩在轨辨识与利用磁力矩器实现剩磁矩主动补偿的新方案:基于磁强计输出和卫星姿态动力学建立了剩磁矩在轨辨识模型,并利用采样滤波器(UKF)提高单磁强计条件下的辨识效果;把控制对象简化成线性定常系统,分析了剩磁干扰力矩对姿态的影响数学模型,并针对磁力矩器和磁强计分时工作的特点,基于叠加性原理提出了基于角速度的剩磁矩主动补偿算法。仿真研究表明,在1000 s内剩磁矩在轨辨识精度为0.001 A·m2量级,主动补偿后,偏航角、滚动角与俯仰角控制误差分别从4.3°、4.6°与2.1°均减少至0.4°以内。提出的方法为类似配置卫星减少剩磁干扰力矩的影响提供了一种新思路。
剩磁;姿态测量与控制系统;在轨辨识;剩磁补偿
立方星是一种质量与体积都极小的低成本卫星,大量采用商用器件,具有很高的功能密度,在国际上广泛应用于航天科学研究与大学教育[1-2]。随着技术的进步,近几年立方星已经呈现出实用化的趋势,如行星实验室公司研制的鸽群对地成像星座。立方星由于质量与功耗极其苛刻的限制,姿态测量与控制系统常选用能易于小型化的磁强计、偏置动量轮和磁力矩器作为星上的敏感器和执行机构,甚至将磁强计复用成定轨敏感器,以提高卫星的功能密度[3-4]。
但是卫星在轨工作时,整星内部会形成一个基本稳定的磁场,称之为剩磁。剩磁不但对某些载荷有影响[5],而且剩磁矩与地磁场相互作用形成剩磁干扰力矩,会严重影响姿态控制的精度。为了减少剩磁对星体扰动的影响,通常在地面开展整星磁补偿实验,即首先利用多台标准磁强计测量并反演出卫星的剩磁矩,然后用小型永磁体安装在星体内部抵消剩磁矩,最后再次测量确认磁补偿的效果。文献[6]利用该方法在转子上安装一个与定子永磁体方向相反、大小相同的永磁体,降低了飞轮的剩磁矩,但是该方法会增加卫星研制过程中的各种成本,并且剩磁控制水平存在限度,不是非常适合立方星。
在轨磁补偿是一种利用磁力矩器来抵消星体剩磁矩的技术方案,能够避免地面复杂的标定和补偿过程,在一些场合具有明显优势。SNAP-1卫星在入轨后才发现星体存在较大剩磁,严重影响了姿态确定与控制系统的正常工作。地面设计了一个二步迭代的方案用于估计星体剩磁矩[7],它首先利用星上估计的角速度作为观测值估计了剩磁矩,但是该角速度测量值也受剩磁矩的影响,所以利用估计出的剩磁矩再对角速度估计做修正,获得更精确的角速度估计值作为下次计算的输入。实际操作中共进行了3次迭代,使用了3天中的3组数据,估计精度大约在0.01 A·m2量级。利用磁力矩器补偿剩磁矩时采用直接扣除方法,没有考虑磁力矩器与磁强计分时工作带来的问题,补偿后的姿态控制精度提高至5°~7.5°。
本文针对磁测磁控结合偏置动量的姿态测量与控制方案,提出了一种仅利用磁强计和磁力矩器实现整星剩磁矩在轨辨识与主动补偿的新方案。它基于磁强计和卫星姿态动力学建立了剩磁矩在轨辨识模型,并利用 UKF算法提高单磁强计条件下的辨识精度和速度;针对磁强计和磁力矩器分时工作的特点,把控制对象简化成线性定常系统,分析剩磁干扰力矩对姿态影响数学模型,基于叠加性原理提出了基于角速度的剩磁矩主动补偿算法。研究表明,本文方法具有所需器件少、不依赖地面辅助等优势,并且剩磁矩辨识精度高、速度快,主动剩磁补偿使得控制误差能小于0.4°,综合效果良好。
1 剩磁矩对控制系统的影响分析
某型立方卫星的姿态确定与控制系统采用磁强计作为姿态敏感器,以偏置动量轮和三轴磁力矩器为控制执行机构。其中,-Y轴安装的偏置动量轮常速旋转,实现星体的被动稳定,X和Z轴磁力矩器控制卫星俯仰通道的姿态,Y轴磁力矩器实现章进动控制。
值得指出的是,由于立方星体积小,磁强计与磁力矩器之间的安装距离很近,磁力矩器工作时产生的磁矩会影响磁强计测量地磁场,所以星上的磁强计和磁力矩器是分时工作的,即在一个控制周期内的一小段时间中,磁力矩器不工作,此时磁强计完成对当地地磁场的测量。

式中,m是卫星剩磁矩,B是地磁场在星体坐标系中的磁感应强度。
该剩磁干扰矩会对卫星的姿态控制产生较为严重的扰动,在立方星上表现得更明显,主要原因是立方星动量轮的质量和尺寸受到严格限制,所以动量轮的角动量普遍偏小,抗干扰能力更差,严重影响了立方星姿态控制精度的提高。
因为立方体卫星部件不可避免地使用磁性元件,并且星上电路中的电流也会激发磁场,所以卫星在轨运行时,立方体卫星本体会存在一个大小、方向未知的剩余磁矩[8]。如果星上工作模式不变,该剩磁场一般较稳定,所以微小卫星除受自身的控制力矩作用外,本体的剩磁矩与地磁场相互作用的形成剩磁干扰力矩[9],
2 剩磁矩在轨辨识技术
为有效减小星体剩磁矩对姿态控制的扰动影响,需要通过估计算法将星体剩磁矩在轨辨识出来。显然,剩磁矩最终影响的是卫星姿态,所以本文建立了一种与姿态耦合的剩磁矩在轨估计算法。
卫星的姿态动力学方程为
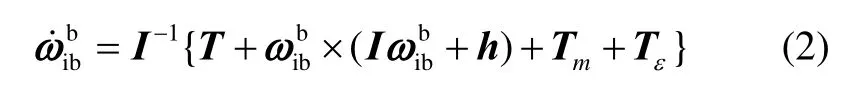
磁强计经过地面标定与在轨标定后,可以认为得到较准确的测量值[10],所以本文选用的磁强计测量模型为

式中,Bc是磁强计输出,B是卫星本体坐标系中地磁场强度的真实值,Bε是磁强计的测量噪声。
将式(1)代入式(2)中,并将式(3)代入式中,则考虑了剩磁干扰的姿态动力学方程为
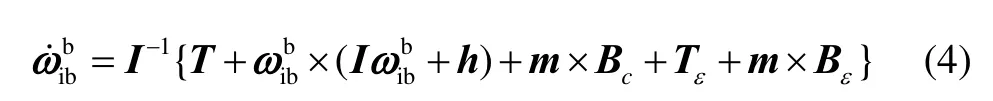
式中,m×Bε表示是由磁强计测量噪声引起的建模不确定度,Tε+m×Bε是系统噪声。剩磁矩在短时间内变化很小,所以建模成

卫星的姿态用四元数q表示,四元数微分方程为

另一方面,在卫星本体坐标系中的磁感应强度B和地心惯性坐标系中的磁感应强度Bi之间的关系为

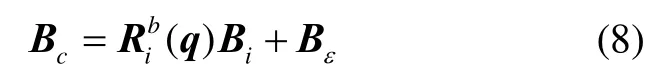
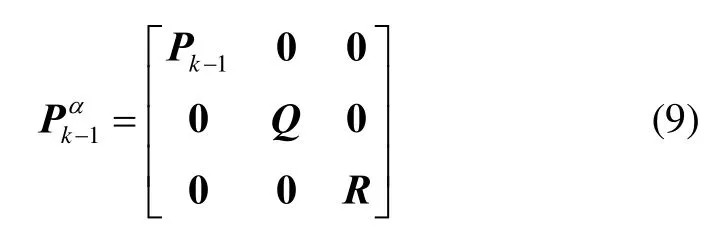
式中:Pk-1是k-1时的状态协方差阵;R=BεB是量测噪声阵;Q是系统噪声阵,计算式为
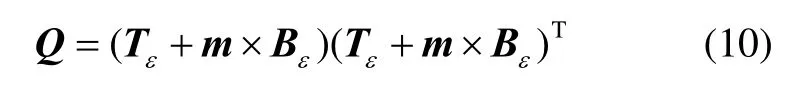
由于式(10)中的m是待估量,在实际滤波中可以采用m当前的估计值来代替,并考虑到Tε和Bε是两个独立的随机分布,则Q的具体计算式为


式中:n是状态量的维数;λ=α2(n+k)-n,是采样比例因子,其中的α来决定采样点的分布,通常取为一个很小的正值,k≥0。
滤波器的时间更新为

滤波器的量测更新为
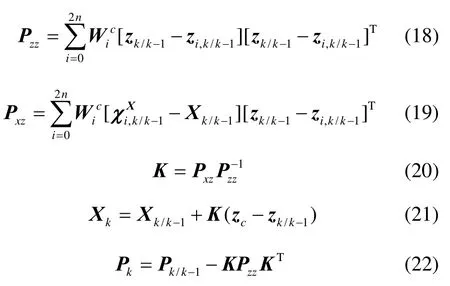
3 剩磁矩在轨主动补偿技术
本节主要论述利用磁力矩器补偿剩磁矩对星体扰动的方法。由于星上的磁力矩器和磁强计采用分时工作方案,所以在一个控制周期内,磁力矩器仅工作部分时间,但是卫星的剩磁矩是和地磁场每时每刻相互作用的,所以磁力矩器不能简单地施加一个与剩磁矩大小相等的反向补偿磁矩。把控制周期的时长记为t,在一个控制周期内磁力矩器的有效时间为t˜。
一般来说,卫星在三轴对地稳定工作模式时,有效载荷正常工作,所以该模式下对卫星姿态控制精度的要求较高,所以剩磁矩在轨补偿算法主要针对三轴对地稳定模式来设计。此时偏置动量卫星的姿态动力学解耦成俯仰通道和滚动偏航通道,分别为

式中,ωx、ωy和ωz是卫星角速度的三轴分量,φ和Ψ是卫星的滚动角和偏航角,ω0是轨道角速率,Ix、Iy和Iz是卫星的三个主转动惯量,Tx、Ty和Tz是控制力矩的三轴分量。
从上述两个微分方程的形式上看,卫星三轴对地稳定时,俯仰通道和滚动偏航通道的姿态动力学方程是线性定常的,所以该系统满足叠加性原理。
因此在分析一个控制周期内的剩磁矩补偿方法时,可以不用考虑控制系统正常的控制过程,所以首先单独考虑考虑剩磁干扰力矩对卫星姿态与角速度的扰动情况。利用第2节方法估计出的剩余磁矩计算剩磁干扰力矩:

因此在一个控制周期末端,俯仰通道产生的扰动角速度为

俯仰通道产生的扰动角度为
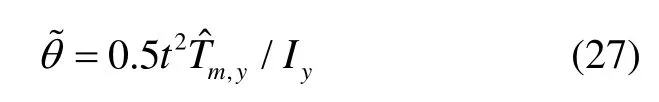
将式(24)离散化,滚动偏航通道在一个控制周期内产生的扰动姿态及其变化率为

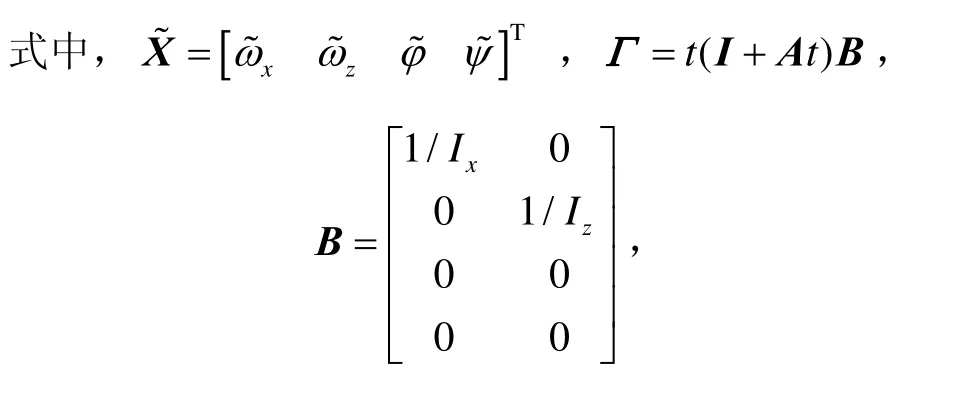
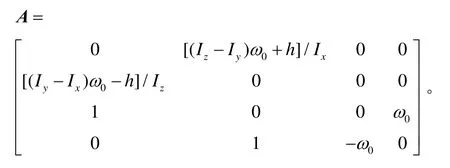
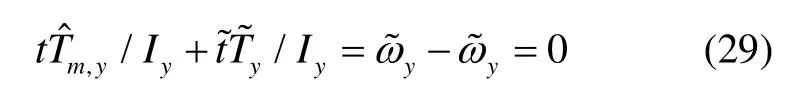
则俯仰通道的补偿磁力矩为

在滚动偏航通道有

则滚动偏航通道的补偿磁力矩为
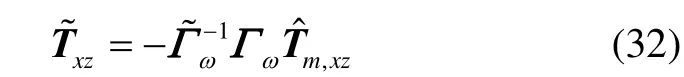
计算出一个周期内的补偿力矩后,利用测量得到的磁场强度 Bc,计算出对应补偿磁矩。记补偿磁力矩为,则补偿磁矩为
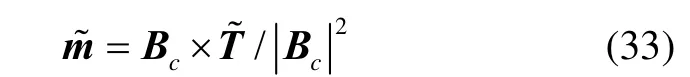
4 仿真与分析
利用数学仿真来验证上述方法的有效性。设定3U立方星运行在高度为 500 km的圆轨道上,轨道倾角42°;三个主轴惯量为[0.0375 0.0375 0.0075] kg·m2,整星质量 4.5 kg;卫星在三轴对地稳定时的角动量指向轨道法向,大小为0.004 Nms;磁力矩器单轴的最大控制磁矩为0.18 A·m2;假定磁强计经过均值处理后的测量噪声为 10 nT(1σ);假定磁强计经过标定后残留的零偏为[100 -8060]nT ;大气密度为 6 ×10-13kg·m3,剩余磁矩矢量设定为[0.01320.01320.0132] A·m2,即整星剩磁矩的模为0.023 A·m2。卫星控制系统的控制周期是 2 s,一个控制周期内磁力矩器的有效作用时间是1.6 s,剩余的0.4 s是磁力矩器的休眠时间。
让卫星原有的控制系统正常工作,并运行于三轴对地稳定状态,仿真时间为8000 s,得到卫星的姿态、角速度等参数如图 2~4所示。在仿真时间内,X、Z两轴的角速率在 0附近,最大角速率误差小于 0.05 (°)/s,Y轴的角速率是轨道角速率;在剩磁等环境干扰力矩作用下,角速度控制误差存在一定变化,这在姿态角控制误差曲线上更为明显,在仿真时间内,偏航角最大误差小于4.3°,滚动角误差小于4.6°,俯仰角误差小于2.1°。滚动偏航通道的控制误差要大于俯仰通道,这是因为俯仰通道时刻有较好的控制能力,而滚动偏航通道的控制能力与在轨地磁场的分布有关,所以更容易受到环境力矩的干扰。从另一方面评价滚动偏航通道的控制效果,绘制角动量与轨道法向的夹角,如图4所示,该夹角最大误差约为5.3°。
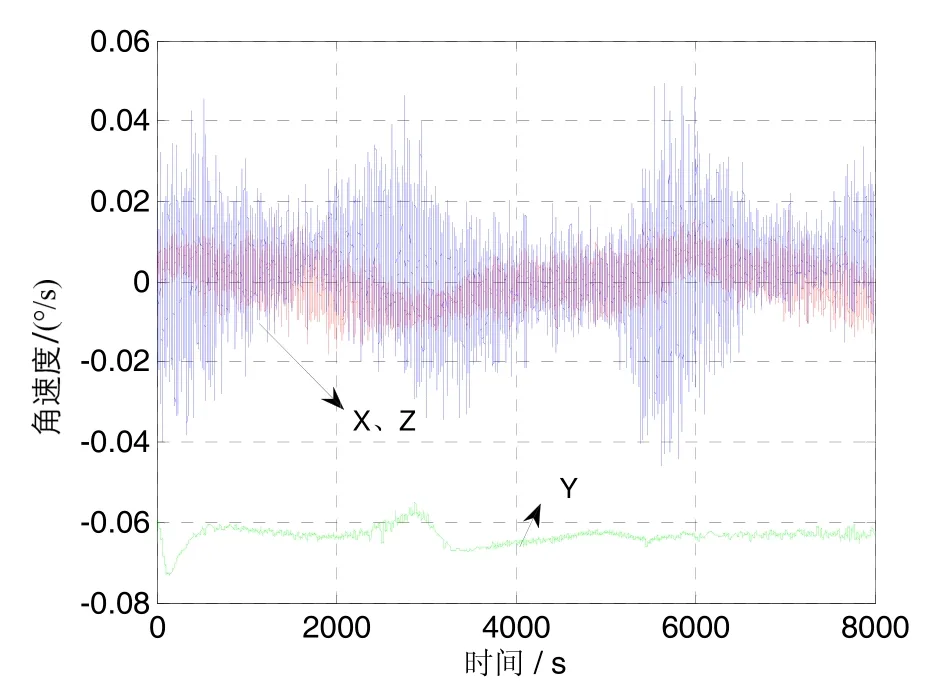
图2 角速度Fig.2 Angular velocity

图3 姿态角Fig.3 Attitude angle
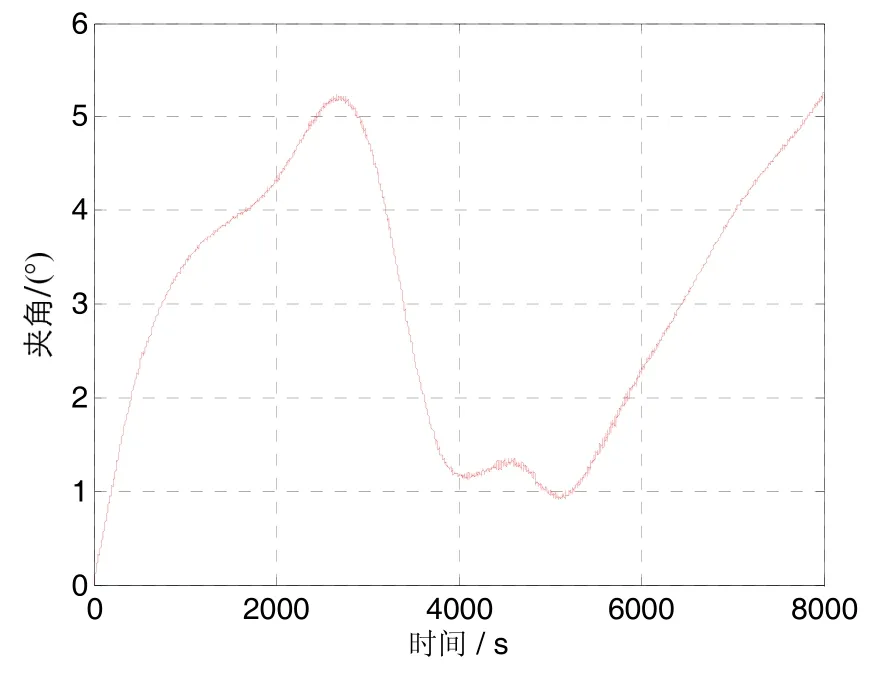
图4 角动量与轨道法向的夹角Fig.4 Angle between angular momentum and the normal of orbit
然后,再次运行该控制软件,同时执行剩磁矩在轨辨识算法模块,运行EKF和UKF两个滤波器,系统噪声阵为 diag(1× 10-10, 1×1 0-10, 1× 10-10)Nm2,测量噪声阵为 diag(400,400,400)nT2,状态误差协方差阵的初值设为 diag[(5°)2,(5°)2,(5°)2,(0.1°/ s)2,(0.1°/s)2, (0.1°/s)2,(0.01A·m2)2,(0.01A·m2)2,(0.01A·m2)2],剩余磁矩估计值初值设为 0;UKF设置的其余参数有α= 0.005, k=0, β=3。EKF和UKF算法对三个轴向的剩磁矩估计误差如图5和6所示。
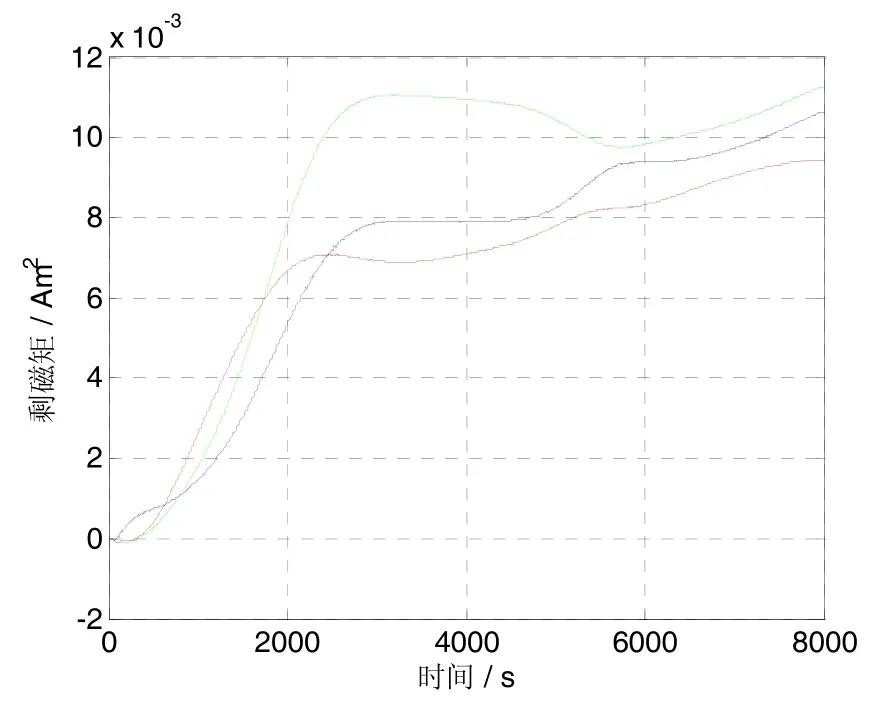
图5 EKF剩余磁矩估计值Fig.5 Remanence estimation using EKF
由上述两个仿真图对比得出,利用单磁强计完成三轴剩磁矩的估计,采用UKF的收敛速度和估计精度都比EKF的效果更佳,EKF算法经过3000 s才完成明显的收敛过程,并且后面的估计曲线仍有较大幅度的波动;UKF在1000 s内就完成了收敛,估计精度也明显提高。在1000s时,UKF对剩磁矩的估计值为[0.0122 0.0119 0.0133] A·m2,相应的估计误差是[-0.0010 -0.0013 0.0010] A·m2;对1000~8000 s内的估计值统计分析,估计均值为[0.0122 0.0124 0.0129] A·m2,估计均方差为[0.00018 0.00016 0.00022] A·m2。
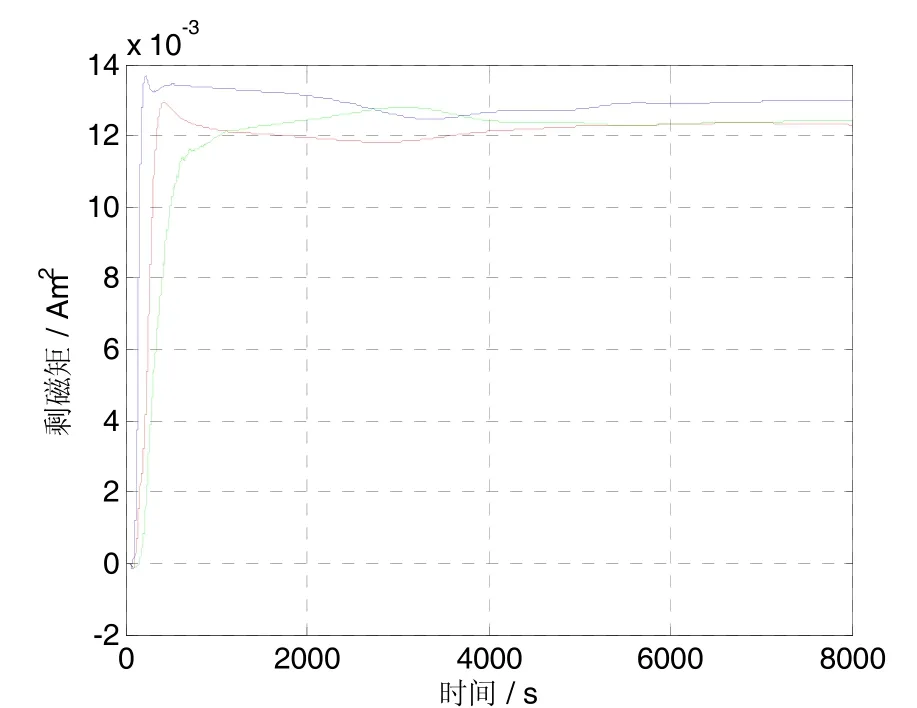
图6 UKF剩余磁矩估计值Fig.6 Remanence estimation using UKF
最后,再一次运行该控制软件,执行UKF剩余磁矩在轨辨识算法模块1000 s,利用1000 s时的辨识结果对剩磁矩分别进行角速度补偿,将补偿值叠加到原控制系统的磁力矩器输出中。
基于角速度补偿算法的结果如图7~图9所示。在仿真时间内,X、Z两轴的角速率在0附近,最大角速率误差仍小于0.05 (°)/s;Y轴的角速率在1000 s后出现了一个扰动,这是由于剩磁补偿加入后产生的。对比图2和图7,在3000 s区域附近,采取主动剩磁补偿措施后的Y轴角速率比补偿前平稳。图8显示,主动磁补偿技术的效果在姿态角控制误差曲线上更为明显,主动磁补后滚动角、偏航角和俯仰角均逐渐减小,在4000 s后可以认为基本收敛稳定,在仿真时间内控制误差小于0.4°,对比图3能够说明基于角速度的剩磁补偿方案的有效性。类似地,角动量与轨道法向的夹角如图9所示,该图描述了在剩磁补偿后,卫星在章进动控制作用下滚动偏航通道的收敛过程。
与文献[5]比较,本文算法取得了更好的效果,其原因有多个方面:1)文献[5]采用了角速度作为观测值,而对比图2和图7,以及图3和图8,可以发现剩磁干扰力矩很小,对角速度扰动影响较小,但是经过长期作用,姿态参数会产生更明显的偏差,所以本文算法通过磁强计输出作为观测值,相当于间接引入了姿态作为观测值,更利于估计剩磁矩;2)UKF算法具有更好的估计性能;3)文献[5]算法采用了二步迭代估计,在角速度估计中不考虑剩磁的影响,在剩磁估计中未考虑角速度误差,如果迭代次数不够多,还是会影响估计精度;4)本论文磁补偿算法推导了较精确的数学模型。为说明本文主动磁补偿算法的性能,采用同样的剩磁矩辨识值,利用文献[5]中的剩磁矩直接补偿方法的控制结果如图10~12所示。

图7 角速度Fig.7 Angular velocity
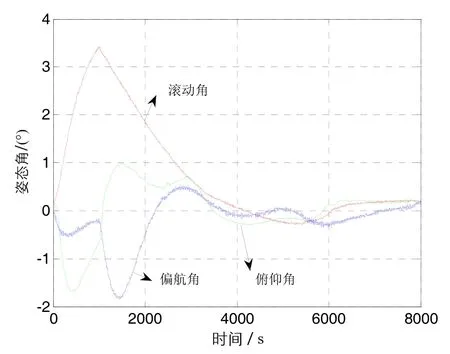
图8 姿态角Fig.8 Attitude angle
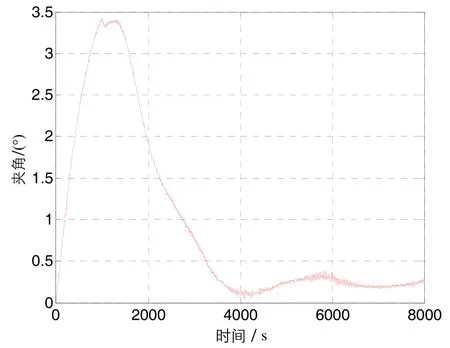
图9 角动量与轨道法向的夹角Fig.9 Angle between angular momentum and the normal of orbit
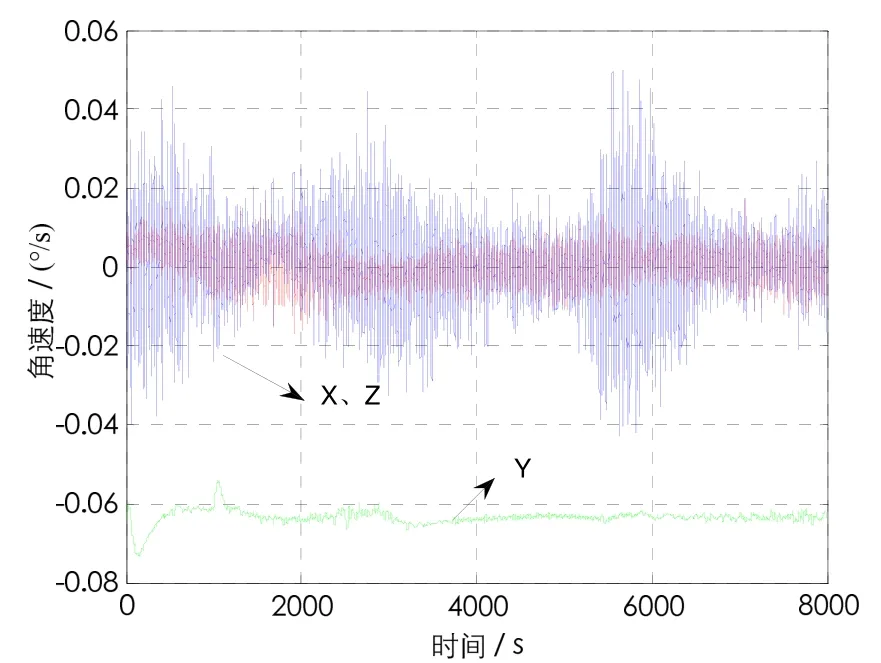
图10 角速度Fig.10 Angular velocity

图11 姿态角Fig.11 Attitude angle
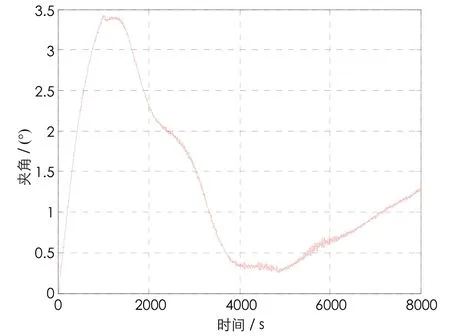
图12 角动量与轨道法向的夹角Fig.12 Angle between angular momentum and the normal of orbit
比较图8与图11以及图9与图12的控制效果,两者的区别仅仅是剩磁补偿方法不一样,虽然已有文献的补偿方法较原系统也有较明显的效果,但是姿态精度比本文方法有明显下降,补偿后的滚动角和偏航角误差已达到1°左右,角动量与轨道法向的夹角在仿真时间内达到了1.3°,这充分说明了本文提出的主动剩磁补偿方案的有效性。
5 结 论
本文提出了一种利用单磁强计实现剩磁矩在轨辨识与利用磁力矩器实现剩磁矩主动补偿的新方法。本方法所需器件少,不依赖地面辅助,并且剩磁矩辨识精度在0.001 A·m2量级,收敛速度小于1000 s,主动剩磁补偿使得控制误差能小于0.4°,综合效果良好。所提方法可以作为类似配置卫星在轨消除剩磁干扰的一个借鉴和参考。
(References):
[1] Boshuizen C R, Mason J, Klupar P, et al. Results from the planet labs flock constellation[C]//The 28th AIAA/USU Conference on Small Satellites, Utah, USA, 2014: 1-8.
[2] 廖文和. 立方体卫星技术发展及其应用[J]. 南京航空航天大学学报, 2015, 47(6): 792-797. Liao Wen-he. A survey of Cubesat technology development and applications[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(6): 792-797.
[3] 郁丰, 华冰, 吴云华, 等. 基于自适应卡尔曼滤波的简化地磁定轨[J]. 中国惯性技术学报, 2014, 22(4): 519-524. Yu Feng, Hua Bing, Wu Yun-hua, et al. Simplified geomagnetic orbit determination based on adaptive Kalman filter[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 519-524.
[4] Wang Xin-long, Zhang Qing, Li Heng-nian. An autonomous navigation scheme based on starlight, geomagnetic and gyros with information fusion for small satellites[J]. Acta Astronautica, 2014, 94: 708-717.
[5] 楚中毅, 任善永. 带柔性伸杆小卫星振动控制的半物理仿真实验[J]. 宇航学报, 2013, 34(6): 748-754. Chu Zhong-yi, Ren Shan-yong. Semi-physical simulation on vibration control of small satellite with flexible manipulators[J]. Journal of Astronautics, 2013, 24(6): 748-754.
[6] 乐韵, 房建成, 汤继强, 等. 磁悬浮反作用飞轮剩磁矩分析与补偿方法研究[J]. 航空学报, 2011, 32(5): 881-890. Le Yun, Fang Jian-cheng, Tang Ji-qiang, et al. Research on analysis and compensation method of remnant magnetic moment for magnetically suspended reaction flywheel[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(5): 881-890.
[7] Steyn W H, Hashida Y. In-orbit attitude performance of the 3-axis stabilized SNAP-1 nanosatellite[C]//The 15th AIAA/USU Conference on Small Satellites. Utah, USA, 2001: 1-10.
[8] Yan Liang, Liu Delong, Jiao Zongxia. Magnetic field modeling based on geometrical equivalence principle for spherical actuator with cylindrical shaped magnet poles [J]. Aerospace Science and Technology, 2016, 49: 17-25.
[9] Lee D, Springmann J C, Spangelo S C, et al. Satellite dynamics simulator development using lie group variational integrator[C]//AIAA Modeling and Simulation Technologies Conference. Portland, Oregon, 2011: 547-566.
[10] Zhang Zhen, Jin Jin, Xiong Jian-ping. Research on attitude determination of micro-satellite with impact of remanence [C]//2013 International Conference on Optical Instruments and Technology: Optical Sensors and Application. Beijing, China, 2013: 1-10.
On-orbit estimation and compensation for CubeSats remanence
LI Ye1, YU Feng2, WANG Qun-yang1
(1. Space Star Technology Co. Ltd., Beijing 100086, China; 2. Nanjing University of Aeronautics and Astronautics, College of Astronautics, Nanjing 210016, China)
A CubeSat usually utilizes magnetometer, magnetorquer and momentum wheel to determination and control its attitude, and the remanence disturbance torque is one of factors that influence the performance of the attitude determination and control system. A new method for realizing the remanence’s on-orbit estimation and compensation is proposed which only utilizes data from the magnetometer and the magnetorquer. First, a remanence on-orbit estimation model is derived by employing the magnetometer outputs and satellite attitude dynamics, and an unscented Kalman filter is utilized to improve the estimation with a single magnetometer. Second, after simplifying the system into a linear time-invariant system, the remanence disturbance which affects the satellite attitude is mathematically modeled according to the superposition principle, and then a remanence compensation method with the criterion of removing angular velocity disturbance is presented in consideration of time-sharing between magnetometer and magnetorquer. Finally, simulations are made which show that the remanence’s estimation accuracy is better than 0.001 A·m2in 1000 s, and the heading, roll and pitch angles are reduced from 4.3°, 4.6° and 2.1° respectively to within 0.4°. The proposed method is a new way to reduce the remanence disturbance for satellites.
remanence; attitude determination and control system; on-orbit estimation; remanence compensation
V448.22
:A
2016-03-23;
:2016-05-28
国家自然科学基金资助项目(61203197)
李烨(1973—),男,高级工程师,从事导航、通信技术研究。E-mail: liyeal@sina.com
联 系 人:郁丰(1980—),男,副研究员,从事微小卫星技术、组合导航技术研究。E-mail: yufeng@nuaa.edu.cn
1005-6734(2016)03-0342-07
10.13695/j.cnki.12-1222/o3.2016.03.012
