基于光纤陀螺的桥梁微小形变检测技术

甘维兵，胡文彬，张 瑶，刘 芳，李 盛，符晶华

（1. 武汉理工大学 光纤传感技术与信息处理教育部重点实验室，武汉 430070；2. 武汉理工大学 光纤传感技术国家工程实验室，武汉 430070）

基于光纤陀螺的桥梁微小形变检测技术

甘维兵1,2，胡文彬2，张 瑶2，刘 芳2，李 盛2，符晶华2

（1. 武汉理工大学 光纤传感技术与信息处理教育部重点实验室，武汉 430070；2. 武汉理工大学 光纤传感技术国家工程实验室，武汉 430070）

桥梁是现代交通运输业最重要的组成部分，形变又是评价桥梁结构健康状况最重要的指标之一。考虑到传统形变检测技术存在诸多不足，为了实现桥梁微小形变的快速、连续检测，准确直观地定位桥跨最大下挠处，提出了基于光纤陀螺（FOG）的微小形变检测新方法，设计出了基于 FOG的桥梁连续线形检测系统（CDMS）。通过对标定路段和大型跨江桥梁结构线形进行测试，并辅以水准仪进行数据比对，结果表明：对于100 m的标定路段，检测精度可以达到5 mm；对于跨径为400 m的跨江大桥，检测精度可以达到2 cm。基于FOG的线形检测系统在桥梁结构测试过程中，无需封路，不影响交通，具有方便、快捷、测量点连续、精度高等特点，尤其是在大跨桥梁的微小形变检测中具有传统技术无可比拟的优势。

桥梁工程；微小形变；光纤陀螺；连续线形；最大下挠

桥梁是现代交通运输业最重要的组成部分。桥梁结构在外力作用下会产生形变，而各种病害如裂缝、预应力损失等最终也将导致桥梁结构发生形变，因而形变是评价桥梁结构健康状况最重要的指标之一[1]。目前形变检测的主要方法有采用光学仪器建立水准控制网进行测量、连通管测试系统、激光测量系统、光电图像式测量系统以及GPS法等新型测试方法。

利用水准测量方法实现对大跨度预应力混凝土箱梁桥挠度变形的监测已经沿用到现在，然而水准控制网的建立过程较为复杂，耗时长，受环境影响较大。王安元[2]在重庆菜园坝长江大桥桥梁荷载试验过程中使用了连通管测试技术，该系统通过测量各测点与基准点的液面压力差来得到各测点的挠度值，不仅需要预铺水管，而且在使用过程中存在着响应时间慢，施工及维护成本高等缺点。熊友谊[3]等人采用激光扫描的方法对桥梁形变进行检测，并辅以精密水准测量进行对比。杨小森、Yan Yu[4-5]等人提出了一种基于倾角仪和振型分解法的桥梁结构挠度测试方法。激光测量系统和光电图像式测量系统主要是通过光学系统捕捉光斑或成像的位置变化得出光源的相对位置变化，这两种测量系统都必须在桥上安装固定设备作为参考点，当设备移动后无法获得最初的测量基准状态，无法满足长期测量要求，而且不同气候条件对测量均有影响。刘浩、Ting-Hua Yi[6-10]等人采用GPS技术对大跨度桥梁结构的承载力进行检测，对形变部位的坐标值进行残差修正补偿，减小转化坐标误差对测量的影响，并提出了采用CFRP加固方法进行数据修复。GPS技术通过接收导航卫星的载波相位差分数据来实时测定站点的三维坐标，是一种新型的实时测量技术。GPS受外界环境影响小，可以在暴风雨中进行监测，可以实现三维坐标的自动监测。然而该技术在测量高程上精度较差，无法达到桥梁结构高精度形变测量要求，且成本较高，易受桥塔或斜拉索的干扰，无法展开大规模应用。

综上所述，传统测量方法均存在检测周期长，实施成本高，测量点不连续等特点，很容易遗漏结构存在的潜在病害部位，难以满足桥梁结构对微小形变检测的快速、连续、精准需求。王立新[11]等人最早于2002年就提出了将光纤陀螺用于工程结构形变测量，张卓敏[12]等人也于2014年提出了将光纤陀螺用于大跨桥梁连续线形检测，两者均采用的是结构形变测量的近似算法，测量误差较大，精度很难得到保证。本文根据光纤陀螺（FOG）对角速度敏感的特性，结合载体运行时提供的高分辨率里程信息，采用微小形变检测新算法推导了FOG用于形变测量的基本原理和方法，设计出了基于光纤陀螺的桥梁连续线形检测系统（CDMS），并将该系统应用于试验段小型拱桥和大型跨江桥梁结构线形测试，其检测精度较高，测试效果良好。

1 光纤陀螺用于形变检测的原理及算法

1.1 光纤陀螺用于形变测量的近似算法

利用光纤陀螺可精确测量载体运动姿态角的特点。采集当载体运动时陀螺仪和加速度计相对惯性空间的转动角速度和线加速度沿运载体坐标系分量，结合里程仪的输出信息，采用捷联矩阵及积分运算方法即可推导出载体的运动轨迹[13-15]。具体描述如图1所示。

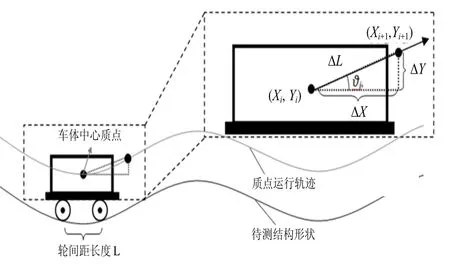
图1 光纤陀螺用于形变测量的基本原理Fig.1 Principle of deformation detection based on FOG

假设运载体从i点运动到i+1点，根据积分极限相似理论，当其运行时间间隔t极限小时，第i+1点的坐标(Xi+1,Yi+1)可以近似表示为：

其中，运载体的线速度为 Vi+1，角速度为 ωi+1，运载体与结构表面的初始夹角为θi。假设载体前后轮间距L是可以忽略不计的，将运载体视为一个质点，根据式(1)和(2)建立的递推函数关系,即可开展运载体沿待测结构表面运行时连续线形轨迹的计算，质点运行的轨迹即为待测结构表面形变曲线。

1.2 光纤陀螺用于微小形变检测的改进算法

在检测结构微小形变时，将载体视为一个质点，用质点运动的轨迹来代替结构表面形变将会给测量带来较大偏差。在实际测量时，运载体承载平台与待测结构表面曲线的位置关系如图2所示，B、A分别为运载体前、后车轮与待测曲线的接触点，前后车轮间距AB为L。当载体沿着结构表面运行时，陀螺的输出与割线AB倾斜角变化直接相关，前、后轮里程计分别记录B、A两点行进的距离。

图2 运载体与待测曲线的位置关系Fig.2 Position relationship between the carrier and the curve

假定A、B两点在曲线f(x)上运动，A、B两点属于刚性连接，在运动过程中距离保持恒定。i时刻A、 B两点在处，i + 1时刻A、 B两点运动到从i到 i+1时刻，B、A两点行进的距离分别为 Δsb、Δsa，其中AiBi与Ai+1Bi+1的夹角为 θi，其输出模型为：

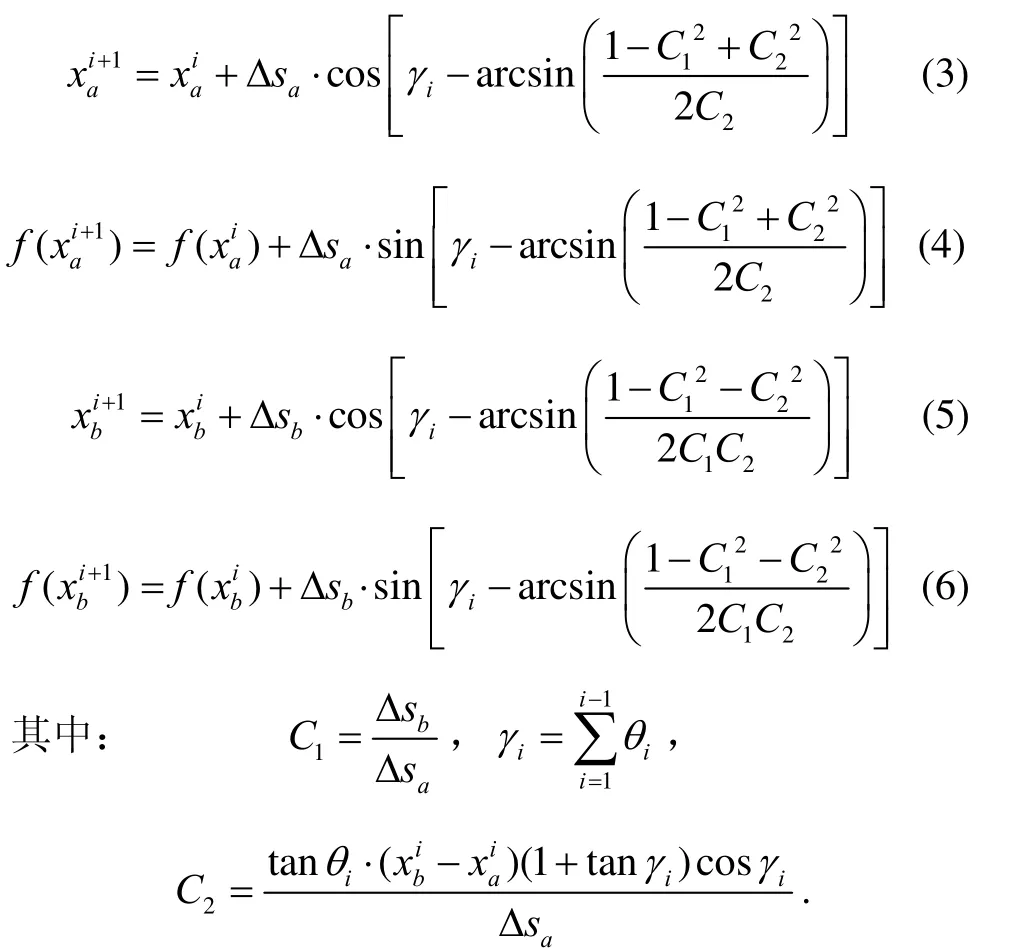
由以上输出模型可知：相比将运载体视为一个质点的近似算法，新算法中的运载体与曲线接触点A、B更好地把握了系统与待测曲线在实际运动中的位置关系，客观地采用割线AB倾斜角的变化反映陀螺的输出，无需考虑割线AB是否近似为切线的问题，其测量结果更加真实、准确，特别适合结构微小形变的精确测量。

2 系统构成及检测精度分析

2.1 系统构成

基于FOG的桥梁连续线形检测系统主要由刚性四轮小车（运载体）、数据采集系统、里程仪及接口电路、蓄电池、光纤陀螺五大部分构成，如图3所示。

图3 基于光纤陀螺的桥梁连续线形检测系统Fig.3 Line-shape detection system for based on FOG

光纤陀螺用来敏感载体运动时的角速度变化，前、后轮高分辨率里程仪用来实时记录载体运行时的里程信息，辅助加装的位置传感器用于修正边界点，减振器用来缓解路面不平整带来的颠簸，便携式计算机用来实时采集和分析来自车体的相关信息。采用刚性四轮小车将以上各种传感器、装置及FOG集成于一体，即可构成基于FOG的桥梁连续线形检测系统。其解算基本思路是将光纤捷联惯导系统及里程计的输出信息进行解算和航位推算就可以得到载体运行的轨迹，再利用起始点位置信息对姿态角误差、里程计标度因数误差进行补偿，就可以确保系统的检测精度。

2.2 检测精度的分析

在实验室水平地面放置一座结构对称的刚性桥模，已知检测小车的几何尺寸长1 m、宽0.6 m，载重30 kg，考虑到检测小车自重对刚性桥形变测试的影响，特在刚性桥底部增加刚性支撑以确保小车自重对形变的影响可忽略不计，从而有效开展形变检测的研究。将检测小车沿其表面推行，其实验系统以及刚性桥模的结构线形、解析式如图4所示，小车运行的轨迹即可表征刚性桥表面线形。

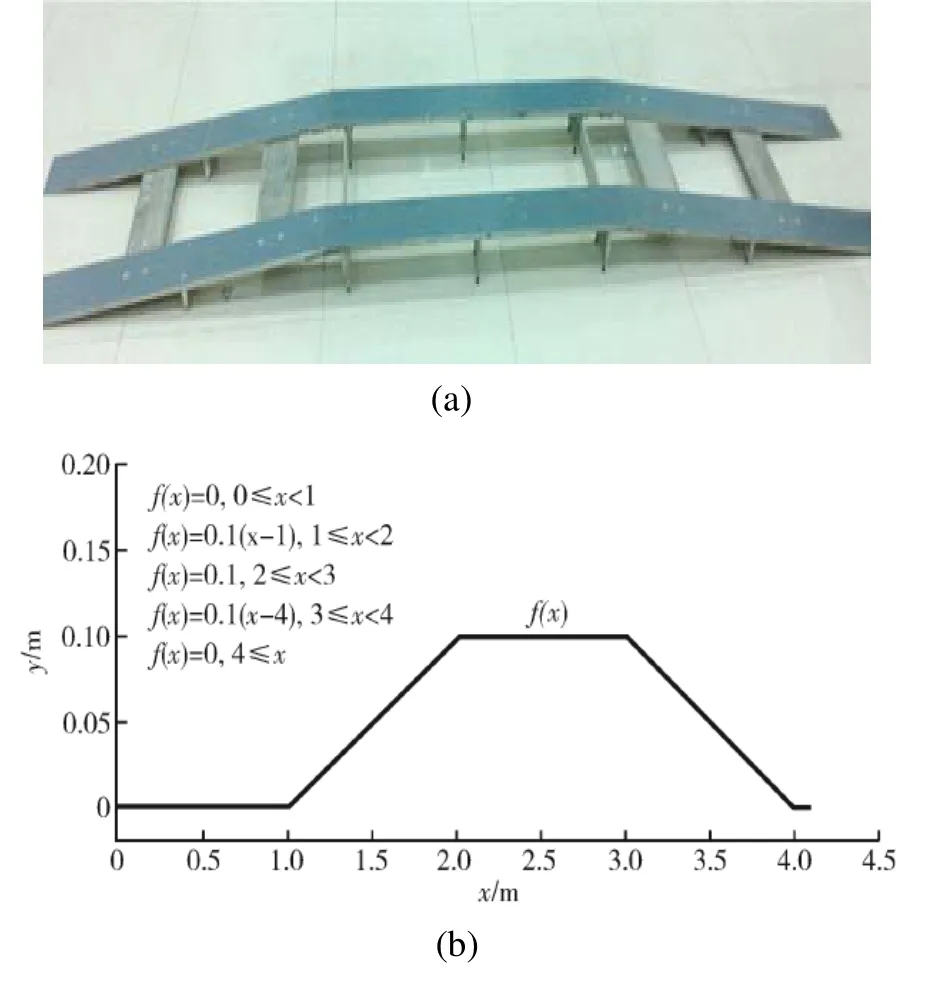
图4 线形检测系统实验Fig.4 Experiment of line-shape detection system

以刚性桥解析式f(x)及基于光纤陀螺形变检测原理为基础进行仿真，可以解算出基于近似、改进算法的线形检测系统经过f(x)时的输出曲线。在改进算法中，将B、A两点行进的距离Δsb、Δsa和AiBi与Ai+1Bi+1之间的夹角θi代入式子(3)至(6)进行积分推演，可得到如图5所示的黑实线，其线形与刚性桥表面的结构线形高度吻合。

在近似算法中，假设运载体的前、后车轮间距L是可调的，从0.8 m逐渐减小到0.05 m，每一个L值均可对应得到一组陀螺输出值，根据光纤陀螺线形检测的原理即可推演出其相应的线形曲线，记为g(x)。该线形曲线表征了系统通过刚性桥f(x)时所测得的结构表面线形，其测量结果如图5所示的散点线。由图5可知：随着运载体前、后车轮间距L逐渐减小，系统解算出的线形曲线g(x) 整体上越来越接近f(x)，当L=0.05 m时，g(x) 与f(x) 基本吻合。

图5 不同结构尺寸的运载体线形检测曲线Fig.5 Detection curves for different sizes of vehicles

由此可知：对于结构微小形变的检测，切不可采用光纤陀螺形变检测近似算法，这样会给测量带来较大偏差；载体前、后轮间距大小与检测精度密切相关，轮间距越小，测量的线形曲线越接近真实值，更加能反映结构的微小形变；改善算法充分考虑了运载体前、后轮行走的距离和割线倾斜角的变化，其测量结果更加真实、准确。

2.3 保障检测精度重要条件

与惯性导航领域中的长距离轨迹测量相比, 基于FOG的桥梁连续线形检测系统在检测过程中具有以下特殊性：1）待测桥梁距离较短，可进行多次重复测试，提高测量精度；2）检测过程耗时较短，环境温度变化小，可忽略时漂、温漂等因素对光纤陀螺自身的影响；3）待测桥梁结构尺寸已知，可利用边界条件对线形数据进行修正。

在测试过程中，光纤陀螺的角速度变化保持在5 (°)/s 以内，陀螺标定因素非线性大约为10-4，对线形的影响非常小。与此同时，考虑到系统误差及陀螺的随机游走误差，系统还采取了初始对准、首尾约束以及已知点校准的方法，从而确保其检测精度。

3 系统的标定与测试

3.1 试验场景

如图6所示，该标定路段为某省道的重要组成部分，双向四车道，设计时速60 km/h，于2012年建成通车，路段全长100 m，路面宽15 m，如图7所示。在标定路段设置6个等距离的标志性坐标，以便线形检测系统与水准测量方法进行数据比对。

图6 标定路段试验场景Fig.6 Test scenario of calibration road

图7 参考点坐标分布Fig.7 Coordinate distribution of reference points

3.2 测试方法

采用水准仪按照图7所示的位置对以上6个标志点进行闭合式测量，计算出其相对起点的高程值。然后，在标定路段两端分别放置位置传感器作为检测小车运行的起点和终点，小车每次测试均从起点开始，终点结束，沿着马路旁边的白直线推行，其运行总里程为100 m。

在线形系统检测前，将检测小车对准即将运行的方向约120 s，采集静态数据以便消除地球自转及系统本身带来的误差；小车检测过程中始终沿着路边白直线推行从而确保轨迹的一致性；通过参考水准仪测试的起点、终点坐标进行校正，减少陀螺的随机游走和发散性误差；沿途设置若干位置传感器准确定位各已知点物理位置，以便检验线形检测系统在各已知点的测量精度。

3.3 标定实验

让检测小车沿着同一路径在标定路段表面空载运行8趟，通过对8趟数据的分析和整理，可知该系统的重复性如图8所示。

从图8可知，横坐标表示起点到终点之间的里程距离，纵坐标表示相对起点的路面标高。从以上8趟数据曲线可以看出：该系统的一致性较好，基本能够反映路面的结构线形；路面微小的不平整度也有所体现；多趟数据的发散性控制在1 cm以内，是因为采用了首尾数据约束的处理方法，从而控制了终点数据的发散性，使得中间里程的数据看起来离散型较大。

考虑到每趟人为推行检测小车带来的不确定性误差，将线形系统（CDMS）在各已知点检测的8趟数据进行平均处理，然后与水准仪测试的数据进行比对，可知该系统的检测精度如表1所示。

由表1可知，线形检测系统处理后的平均值与水准仪测试的数据十分接近，最大误差为5 mm。

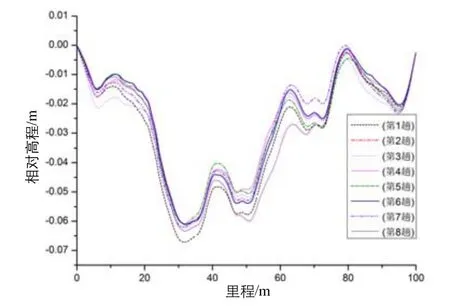
图8 线形系统重复性测试Fig.8 Repeatability of the CDMS

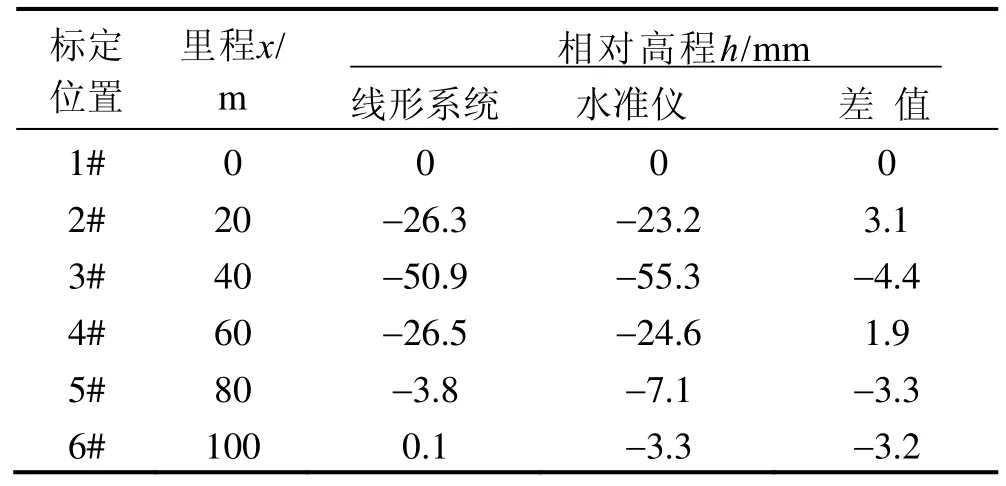
表1 线形检测系统与水准仪测试的数据对比Tab.1 Comparison of CDMS and level gauge

3.4 实验小结

由图8可知，系统在测试100 m路段的形变时，其重复性良好，最大偏差在1 cm以内，且能够检测到路面微小不平整度；由表1可以看出：采取多趟数据平均和首尾约束的处理方法可以大大提高系统的检测精度；检测的速度很快，100 m的待测路面大约在8 min左右完成，基本上可以不考虑温度漂移对光纤陀螺的影响；其检测精度较高，满足结构工程测量对精度的要求。

4 实桥测试

4.1 工程概况

某跨江大桥是长江上第一座特大型预应力混凝土斜拉桥，是国家“八五”期间重点建设项目。大桥全长4407.6 m，主桥为双塔双索面钢筋混凝土斜拉桥，跨径为180 m +400 m +180 m，宽26.5 m，设6车道，H型主塔高153.6 m，高强平行钢丝斜拉索。该桥日通车能力50 000辆，于1995年6月通车，如图9所示。

图9 某跨江大桥概貌Fig.9 Overview of a river-crossing bridge in China

4.2 主桥连续线形测试

为了进一步验证线形系统在实际桥梁应用中的可靠性和检测精度，利用该系统完成某跨江大桥主体桥梁结构连续线形检测工作，且在部分区域采用水准仪对控制点相对高程进行复核，其主体桥梁连续线形曲线如图10所示。

由表2可知，两者在各控制点的相对误差控制在1.5 cm以内，相对于主跨径（11#和12# 墩之间）为400 m 的斜拉索桥，其检测精度已经达到了较高的水平。

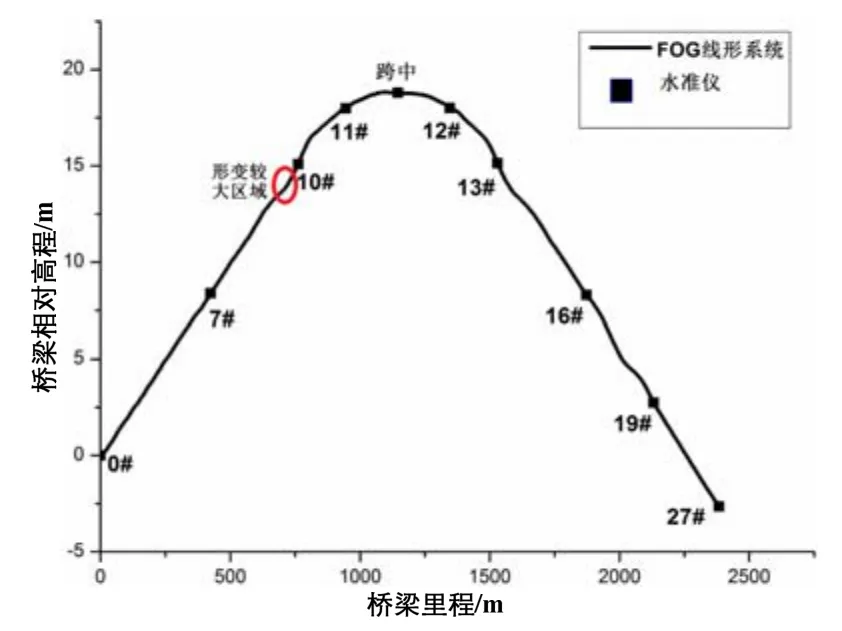
图10 主体桥梁连续线形曲线Fig.10 Major bridge’s continuous line-shape curve

表2 CDMS与全站仪在各控制点的相对高程对比值Tab.2 Comparison on CDMS and indicator

4.3 最大下挠处定位

由于CDMS采用连续测量方法，运载体所经过之处，其结构线形随即输出。通过对桥梁主体结构线形进行观察、分析，发现9#~10#墩之间存在变形较大区域，我们将该段数据进行精细化处理、分析，发现两跨之间的最大变形区域并非跨中，而是偏离跨中23 m左右，如图11所示。通过采用水准仪对该点进行重新复核，验证了该系统的可靠性和准确性。

图11 桥梁结构最大下挠处的准确定位Fig.11 Precise locate the maximum deflection of bridge structure

4.4 试验小结

从图10可知，沿桥纵向主梁形变是对称的，与桥梁结构对称的特性是相符的；由表2可知，线形系统测得的相对高程值与高精度全站仪最大偏差为 1.5 cm；由图 11可知，线形系统能够准确的定位桥梁结构最大下挠处，不会遗漏结构存在的任何病害处。对于400 m 跨径桥梁而言，当相对高程差达到米级时，该测量精度满足工程测量要求。

5 结 论

基于光纤陀螺的连续线形检测系统借助运载平台对结构表面进行移动式检测时，待测结构表面无需安装任何传感器，在检测过程中无需封路，不影响交通，具有方便、快捷、测量点连续、精度高等特点；该系统使用便捷、移植灵活，对于中小型桥梁可以选择小推车作为运载体进行检测，对于大跨度桥梁可以采用小汽车作为载体进行检测；该检测系统具有测量点连续的特点，能够准确定位桥跨最大下挠处，不遗漏任何病害部位，尤其是在大跨桥梁的微小形变检测中具有传统技术无可比拟的优势。

该技术已经在30多座大、中型桥梁结构线形测量中得到推广使用。与此同时，该技术同样适合高速公路路面不平整度的检测、机场轨道和高速铁路轨道不平顺性测试以及煤矿巷道形变检测，值得推广应用。

（References）：

[1] JTG/T J21-2011. 公路桥梁承载能力检测评定规程[S].北京: 人民交通出版社, 2011. JTG/T J21-2011. Specification for inspection and evaluation of load-bearing capacity of highway bridges[S]. Beijing: People's Communication Press, 2011.

[2] 王安元, 陈县伟, 张强. 桥梁荷载试验挠度测量方法的运用[J]. 工程与试验, 2012, 52(1): 31-33. Wang An-yuan, Chen Xian-wei, Zhang Qiang. Application of defection measurement methods to bridge loading test[J]. Engineering & Test, 2012, 52(1): 31-33.

[3] 熊友谊, 陈宜金, 冯志新, 等. 基于地面激光扫描的三山南桥载荷变形监测研究[J]. 测绘与空间地理信息, 2012, 35(8): 26-29. Xiong You-yi, Chen Yi-jin, Feng Zhi-xin, et al. The research on load-generated deformation monitoring of Sanshan South Bridge based on terrestrial laser scanning[J]. Geomatics ＆Spatial Information Technology, 2012, 35(8): 26-29.

[4] 杨小森, 闫维明, 陈彦江, 等. 基于倾角仪的桥梁挠度测试方法研究[J]. 土木工程学报, 2010, 43(增): 106-111. Yang Xiao-sen, Yan Wei-ming, Chen Yan-jiang, et al. Bridge deflection testing method based on utilization of inclinometers[J]. China Civil Engineering Journal, 2010, 43 (Supplement): 106-111.

[5] Yu Yan, Liu Hang, Li Dong-sheng, et al. Bridge deflection measurement using wireless MEMS inclination sensor systems[J]. International Journal on Smart Sensing and Intelligent Systems, 2013, 6(1): 38-57.

[6] Roberts G W, Cosser E, Meng Xiaolin, et al. High frequency deflection monitoring of bridges by GPS[J]. Journal of Global Positioning Systems, 2004, 3(1): 226-231.

[7] Yi Ting-Hua, Li Hong-Nan, Gu Ming. Experimental assessment of high-rate GPS receivers for deformation monitoring of bridge[J]. Measurement, 2013, 46(1): 420-432.

[8] 刘浩, 王婷婷. 大跨度桥梁结构的承载力检测及加固方法研究[J]. 科技通报, 2013, 29(7): 204-207. Liu hao, Wang Ting-ting. The bearing capacity of the large span bridge structure detection and strengthening methods[J]. Bulletin of Science and Technology, 2013, 29(7): 204-207.

[9] Meng X, Dodson A H, Roberts G W. Detecting bridge dynamics with GPS and triaxial accelerometers[J]. Engineering Structures, 2007, 29(2): 3178-3184.

[10] 谭庆. GPS在铁路工程测量中的应用探讨[J]. 黑龙江交通科技, 2014(10): 70-71. Tan Qin. Discussion on the application of GPS in the measurement of the railway engineering[J]. Heilongjiang Traffic Science and Technology, 2014(10):70-71.

[11] 王立新, 胡文彬. 光纤陀螺应用于轨迹测量的实验研究[J]. 武汉理工大学学报, 2002, 24(8):50-52. Wang Li-xin, Hu Wen-bin. Experimental study of trajectory measurement used with fiber optical gyro[J]. Journal of Wuhan University of Technology, 2002, 24(8): 50-52.

[12] Zhang Zhuo-min, Hu Wen-bin, Liu Fang, et al. Vibration error research of fiber optic gyroscope in engineering surveying[J]. Telkominka-Indonesian Journal of Electrical Engineering, 2013, 11(4): 1984-1955.

[13] 戴洪德, 柳爱利, 卢建华, 等. 舰船波浪中航行时的变形分析及其IMU实时测量方法[J]. 中国惯性技术学报, 2014, 22(3): 327-332. Dai Hong-de, Liu Ai-li, Lu Jian-hua, et al. Deformation analysis and IMU-based real-time measuring method for big ship sailing in wave[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 327-332.

[14] Zheng J, Qin S, Wang X, et al. Influences of gyro biases on ship angular flexure measurement[C]//Proceedings of 2011 Symposium on Photonics and Optoelectronics. Wuhan, China, May 16-18, 2011: 1-4.

[15] Yang Yun-tao, Wang Xing-shu, Huang Zong-sheng, et al. Compensation for observed coupling effect in measuring angular deformation of ship hull by laser gyroscope units[J]. Journal of Chinese Inertial Technology, 2014, 22(5): 561-566.

Detection technique for bridge’s micro-deformation based on FOG

GAN Wei-bing1,2, HU Wen-bin2, ZHANG Yao2, LIU Fang2, LI Sheng2, FU Jing-hua2
(1. Key Laboratory of Fiber Optic Sensing Technology and Information Processing of Ministry of Education, Wuhan University of Technology, Wuhan 430070, China; 2. National Engineering Laboratory for Fiber Optic Sensing Technology, Wuhan University of Technology, Wuhan 430070, China)

Bridge is an important part of modern transportation systems, and the deformation is a key index for bridge’s safety evaluation. Considering that the traditional deformation detection technology has many shortcomings, a continuous deformation measurement system (CDMS) based on fiber optic gyroscope is presented and validated to rapidly achieve the curve measurement of long-span bridge and to timely and accurately locate the bridge’s maximum deflection. Experiments on the structure profiles of the calibration road and the solid bridge are made, aided by data comparison with leveling instruments. The results show that the detection accuracy can reach 5 mm for 100 m model bridge, and the detection accuracy can reach 2 cm for the solid bridge with the span of 400 m. The CDMS has no influence on the testing process, which has the advantages of convenient, fast, continuous measurement and high accuracy, especially in large-span bridges.

bridge engineering; micro deformation; fiber optic gyroscope; continuous linear; maximum deflection

U666.1

：A

2016-01-26；

：2016-05-16

国家自然科学基金资助项目（61402345）；国家科技支撑计划课题任务书（2014BAG07B01）；

中央高校基本科研业务费专项资金资助项目（WUT: 2014-II-012 , WUT: 2014-IV-009）

甘维兵（1978—），男，博士，副教授，从事光纤传感应用研究。E-mail: ganweibing@whut.edu.cn

1005-6734(2016)03-0415-06

10.13695/j.cnki.12-1222/o3.2016.03.025