考虑防御系统延迟使其预测误差最大的突防弹道设计

齐乃明 ，周 啟航,2，崔乃刚，董 程,3

（1. 哈尔滨工业大学 航天学院，哈尔滨 150001；2. 北京宇航系统工程研究所，北京 100076；3. 北京航天新风机械设备有限责任公司，北京100854）

考虑防御系统延迟使其预测误差最大的突防弹道设计

齐乃明1，周 啟航1,2，崔乃刚1，董 程1,3

（1. 哈尔滨工业大学 航天学院，哈尔滨 150001；2. 北京宇航系统工程研究所，北京 100076；3. 北京航天新风机械设备有限责任公司，北京100854）

对中段多脉冲机动突防弹道的设计问题进行了研究。采用的原理与方法有别于成熟的航天器多脉冲变轨，而是基于路径规划的思想对弹道设计问题简化。考虑敌方防御系统延迟，改进多脉冲点火模型,并基于变射面的思想对关机点参数进行了设计及优化。然后，从使敌方预测误差最大的角度提出评价函数，并利用遗传算法进行优化。最后，给出了一种同时满足导弹机动突防与打击精度要求的多脉冲弹道设计方法。从模型的可行性，方法的有效性、灵活性、迭代效率及精度等方面进行了仿真验证分析。在PC机仿真中，20 s内就设计出一条保证打击精度的中段突防弹道。结果表明，建立的模型是可行的，提出的突防弹道设计方法是快速有效的。

多脉冲；预测误差；系统延迟；变射面；机动突防

导弹防御系统可在弹道导弹的中段对其进行多次拦截与毁伤评估[1]，所以大部分拦截策略都以中段拦截为研究对象。传统弹道导弹打击目标时，关机后弹道固定，极易在中段被敌方防御系统探测与拦截。因此，中段突防对弹道导弹极为重要，直接决定导弹打击任务的成败[2]。中段机动突防可以有效提高导弹的突防能力，但是需要考虑打击精度问题，限制了机动突防能力的充分利用。多脉冲机动可以快速有效地改变及修正弹道[3-4]，缩短敌方预警时间，增加敌方预测误差，从而提高导弹的突防能力。在保证打击精度的前提下，如何利用多脉冲机动使导弹的突防能力最大化成为了研究热点。

文献[5]提出了在弹道最高点利用单脉冲点火变轨的突防策略，但只考虑了单脉冲变轨的情况；文献[6]基于hp-伪谱法的对大气层内的飞行器轨迹进行了设计与优化，但没考虑突防的问题；文献[7-8]提出了利用多脉冲增加敌方探测系统预测误差的突防策略，但脉冲机动后如何保障打击精度则没有考虑；文献[9-10]提出了中段脉冲轴向机动变轨的突防策略，给出了详细的弹道设计方法与仿真算例，但是文献[9-10]中给出了的脉冲变轨方程组不封闭的，需要额外给出封闭条件，此外也没有考虑最优变轨点问题[12]。

为了克服上述多脉冲弹道设计方法的局限性，本文借鉴路径规划的思想，提出了一种新的多脉冲点火模型，将弹道设计问题转变成变步长搜索的路径规划问题，提出了一种能保证提高导弹机动突防能力的弹道设计方法。通过数值仿真验证了多脉冲点火模型可行性、弹道设计方法的有效性。

1 弹道设计问题描述

目前，成熟的航天器多脉冲变轨原理和方法大部分是以卫星或飞船为研究对象得到的，但是导弹脉冲变轨与卫星脉冲变轨不能等同而论[9-10]。

1.1 问题分析

本文需要解决的问题是：给出快速精确且同时满足导弹机动突防与打击精度要求的多脉冲弹道设计方法。采用文献[9-10]中的假设条件：

1）不考虑地球自转、空气阻力，视其为匀质球体[8-11]；

2）敌方防御系统确定来袭导弹的弹道需要的最短时间为τ（一般4~6 min），称之为防御系统延迟[8]；

3）假设每次脉冲点火后，有一“虚拟导弹”沿着点火前的弹道继续飞行，其飞行弹道为“虚拟弹道”。

根据以上假设，从以下方面对弹道进行设计：

1）为了降低被敌方防御系统确定和拦截的概率，导弹在时间τ内完成脉冲变轨，使敌方防御系统对弹道的预测误差无法收敛，从而无法满足拦截的条件。导弹发射前，初始关机点参数已基于“变射面思想”进行优化。使导弹在初次关机时，其落地点为一个与真实目标有较大差距的虚拟目标，从而缩短敌方预警时间。

2）将由机动造成的敌方预测误差Ri作为点火前后弹道差异的量化指标。通过优化使Ri最大，从而使弹道对敌方的迷惑及缩短其预警时间的效果达到最大。在脉冲变轨的同时完成弹道修正，使导弹逐步逼近直至最后击中目标[3-4]。

弹道设计的具体步骤如下：

1）根据真实的打击目标选取参考弹道，得到其关机点参数。依据点火次数n，将多脉冲弹道分解成n+1段子弹道，提取点火间隔、点火参数等优化变量。

2）视点火点为搜索扩展的节点，每段子弹道的飞行距离为搜索步长。将多脉冲弹道设计问题转化成变步长的路径规划问题。以Ri最大化为优化目标，采用智能算法对弹道进行优化。

1.2 问题转化

将脉冲点火点看成节点，以子弹道的射程角fi（对应飞行时间ti）为搜索的步长。多脉冲弹道设计如图1所示。

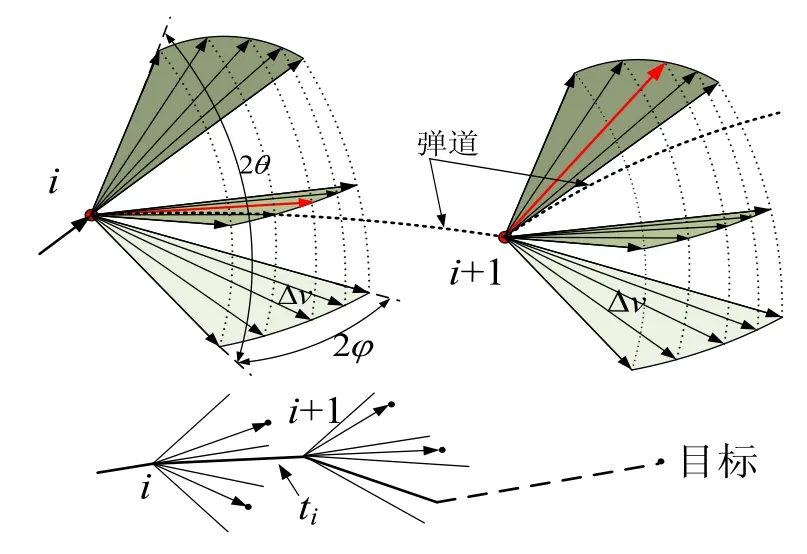
图1 多脉冲弹道节点搜索示意图Fig.1 Schematic for searching the multi-pulse ballistic node

图1中i、1i+为点火点，Δv为脉冲增量，2θ、2φ为发动机喷管弹道面及垂直弹道面两个方向上允许调节的最大角度。脉冲点火时，Δv被限制在一个由四棱锥和球面所包围的区域内。四棱锥在顶点的纵向张角等于2θ，在垂直于弹道平面的张角等于2φ，球面半径等于 vΔ ，其中θ、φ、vΔ 由点火点脉冲增量决定。弹道设计时，将这个区域分成M个扇面，并将每个扇面分成N个扇区。在每个点火点选择一个扇区，通过n次选择得到一条弹道，最后形成弹道集合。在弹道设计中，只需要保证搜索步长ti小于敌方防御系统延迟τ就可以满足导弹突防要求。采用上述方法将多脉冲弹道设计问题转化为路径规划问题，如图2(c)所示。

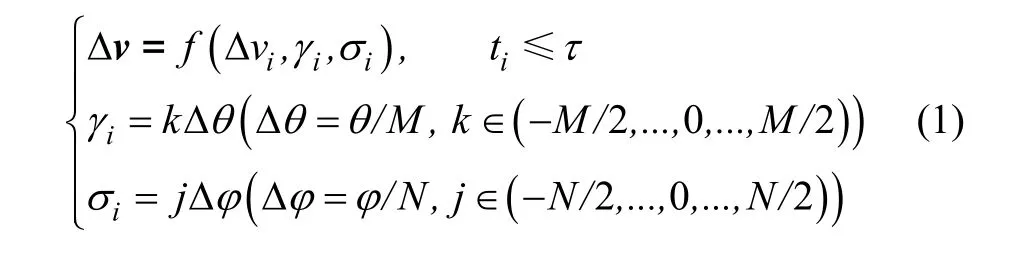
式中：σi为Δv在xoz面投影与x轴的夹角，γi为Δv与平面xoz的夹角，σi、γi表示第i次点火时选择扇形区域的位置，M、N为正的偶数。

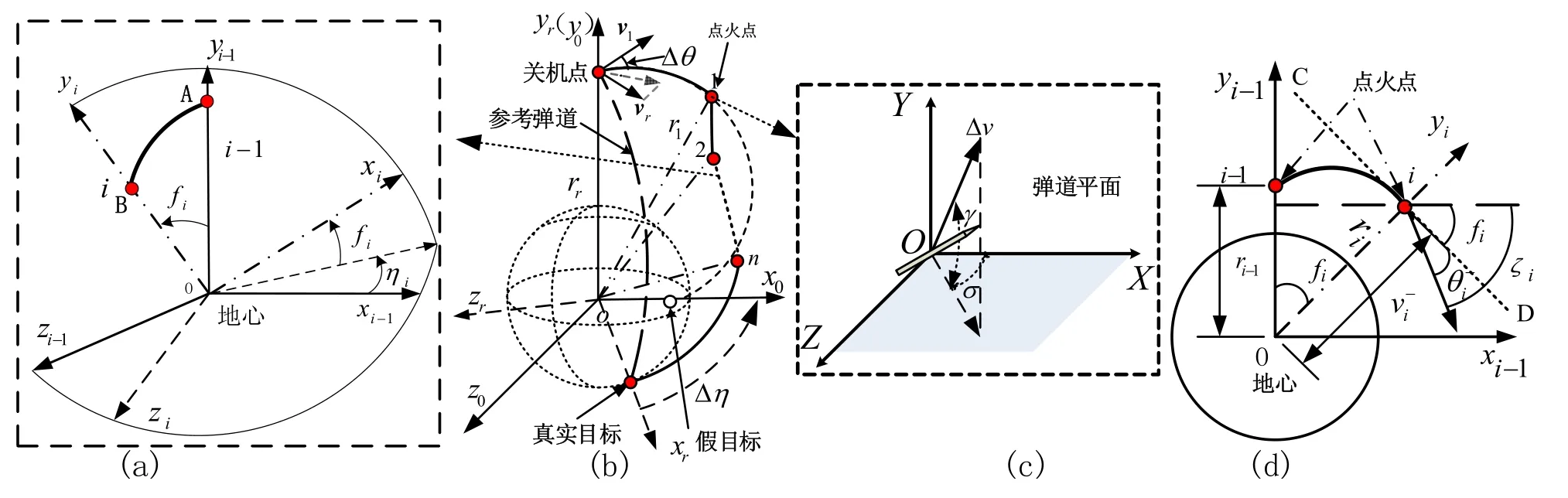
图2 多脉冲弹道示意图Fig.2 Schematic of multiple-pulse ballistic trajectory

2 动力学模型

2.1 基本定义

2.1.1 坐标系定义

基本坐标系定义（如图2(a)所示）如下：

参考坐标系(G(r) :o- xryrzr)：以地心为原点，地心与参考弹道的关机点的连线为yr轴，在参考弹道面内过球心且垂直yr轴指向实际目标点的直线为xr轴，按照右手定则确定zr轴；

子坐标系(G(i):o- xiyizi)：以地心为坐标原点，地心与点火点连线为 yi轴，在当前弹道平面内过地心并且垂直 yi轴指向当前虚拟目标的直线为 xi轴，按照右手定则确定 zi轴；o - x0y0z0的 y0轴为脉冲弹道的初始关机点与地心的连线。

2.1.2 弹道约定

本文选取由关机点到真实目标点之间的能量最省弹道为参考弹道，如图2(b)中虚线所示。其关机点的极半径、速度、弹道倾角、方位角记为(rr,vr,θr,ηr)。

图2(b)中实线部分为多脉冲弹道，1、2、…、n为脉冲点火点。令多脉冲弹道与参考弹道在关机点处二者的极半径、速度等参数相同，弹道倾角与方位角等参数不同，即：

式中：Δ θ 、Δη 分别为多脉冲弹道与参考弹道在关机点处弹道倾角与方位角的差值。

虚拟目标与真实目标之间的差距由 Δθ 、Δ η 决定。基于变射面的思想对 Δθ 、Δη 进行优化，使虚拟目标与真实目标差距最大，从而缩短敌方预警反应时间，提高导弹的突防能力。

相邻两次点火点i、i +1之间的弹道为子弹道（如图2(a)所示）。导弹在 i-1次点火后，以点火点A作为关机点，在 G (i -1)中按照开普勒轨道定律飞行。飞行到B点时，进行第i次点火，此时点火点极半径为 ri，该段弹道的射程角为 fi，飞行时间为 ti，点火前后弹道面的夹角为 ηi。从 G (i)到 G (i -1)的转换矩阵Li（fi,ηi）为：

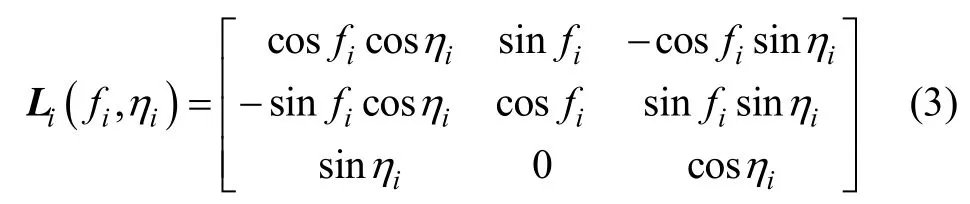
同理， G (r)到 G (0)转换矩阵为 L0（Δη）。

2.2 脉冲点火模型

以子弹道的飞行时间 ti为核心，建立模型。通过ti，将τ导入到所建立的模型中：

1）依据点火次数将弹道分解成 n+1段子弹道,将其分解到 n+1个共原点的子坐标系中。在每个子坐标系内都将点火点视作子弹道的关机点，以点火后的弹道参数作为关机点参数来计算该段子弹道；

2）通过计算坐标系之间的转换关系得到点火前后弹道参数的关系。

图2(d)表示导弹第i-1次点火后在 G(i-1)中的子弹道，[ri-1,vi-1,θi-1]表示关机点的极半径、速度、弹道倾角。第i次点火前，v与yi-1的夹角为 ζi，弹道倾角为θi-。i-1次点火后导弹的参数：

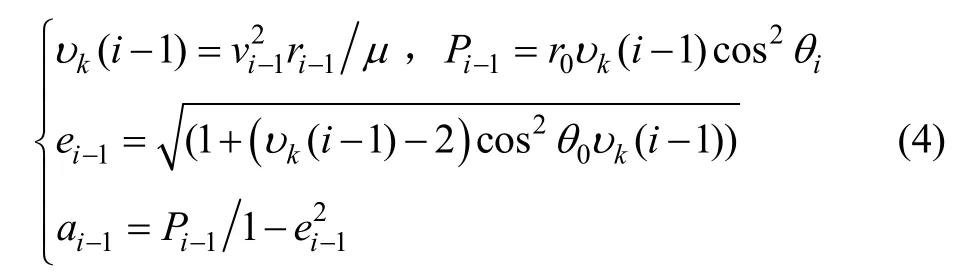
导弹飞行 ti后，偏近点角为 E-1，极半径、速度、弹道倾角分别为。第i次点火前，导弹的位置速度：

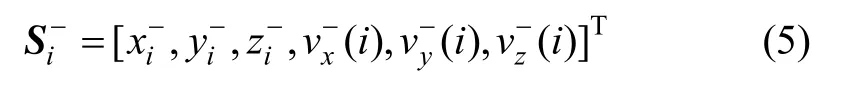
第i次点火时，脉冲增量为 Δvi，点火角度为σi,γi。点火后导弹在 G (i -1)中速度为：

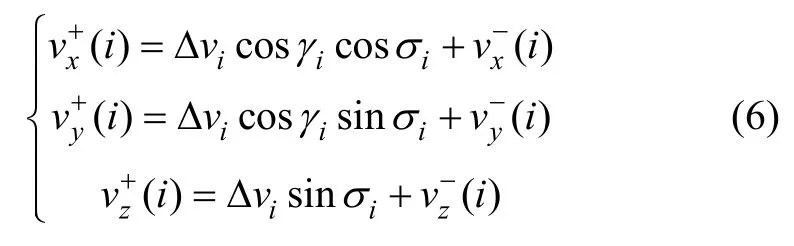
点火前后弹道面的方位角差值为：

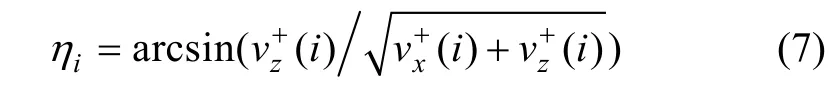
G (i)中的 yi轴为点火点与地心的连线，yi轴垂直当地水平面，即 xi轴与当地水平面平行，所以点火后当地弹道倾角为：

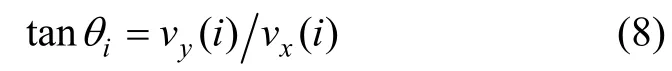
在 G (i)中将 Si、θi作为关机点参数计算第 i+1次点火前的子弹道。

G (r)到 G (i)的转换矩阵 Ci为：

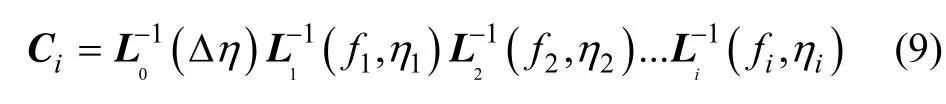
经过n次点火，导弹在G(r)中的落地点坐标为(xtf,ytf,ztf)。

3 多脉冲弹道优化

3.1 优化变量

选取多脉冲弹道与参考弹道在关机点处弹道倾角差值Δθ、方位角差值Δη、子弹道的飞行时间 ti、脉冲作用方向 γi、σi作为优化变量。假设一共点火n次，则变量个数为3n+2，即：

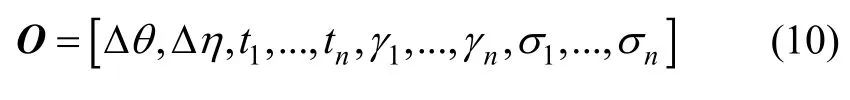
3.2 优化约束

3.2.1 优化变量约束条件

根据前面分析，导弹要突防成功必须保证每段子弹道的飞行时间小于敌方防御系统的延迟时间，即：

多脉冲弹道与参考弹道在关机点的弹道倾角差值及方位角差值的取值范围为：

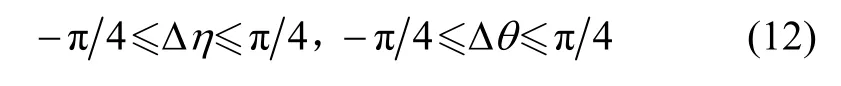
3.2.2 边界约束条件

弹道设计中的边界约束为初始及终端约束。初始约束为参考弹道关机点参数(rr,vr,θr,ηr)，终端约束为目标坐标（xt,yt,zt）。

非线性约束转化为等式约束 Ei及不等式约束C：

式中，R为地球半径。

3.3 优化指标

在多脉冲变轨问题中，通常以时间和燃料作为优化指标。本文除了考虑飞行时间最优以外，还考虑脉冲弹道对敌方探测系统造成的预测误差 Ri。通过 Ri对弹道的突防能力进行量化的评价，寻找使其突防能力最大的最优变轨点。

3.3.1 “虚拟弹道法”

“虚拟弹道”表示敌方防御系统依据导弹点火前的弹道数据对点火后导弹位置的预测。在下次点火或落地时，导弹与“虚拟导弹”的距离为 Ri(预测误差)。如图3中所示，1,2,…,i,…n代表脉冲点火点， n+1代表最终落地点，2’,...,i’,n’代表点火后τ时刻“虚拟导弹”所处位置，R1,R2,...,Ri,...Rn表示两者之间的距离。

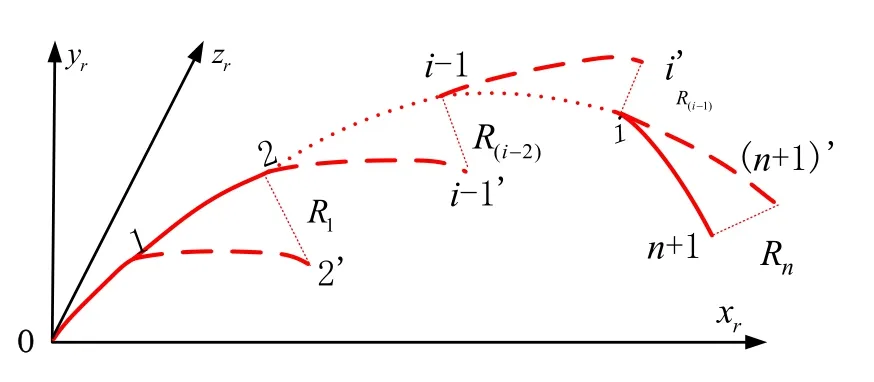
图3 虚拟弹道示意图Fig.3 Schematic of virtual ballistic trajectory

3.3.2 性能指标函数选取

防御系统对导弹的弹道预测都是基于前面弹道观测的结果，其对τ时刻后导弹位置的预测值在导弹变轨前的椭圆弹道上。如果每次点火时导弹的实际位置与“虚拟导弹”的位置距离Ri越大，说明点火前后弹道之间的差别越大，那么敌方探测系统丢失目标概率及拦截器没有足够的机动能力进行拦截的可能性就越大。因此，本文将每一段弹道的Ri作为优化指标，相应的指标函数如下：

式中： Tt为总飞行时间； wi为权值，且都大于零；U为惩罚系数。

4 仿真验证与结果分析

4.1 仿真参数

本文选取文献[10]中多脉冲弹道设计的例子进行仿真，并以此作为对比。导弹关机点参数为：rr=6491 km，vr=5.137 km/s， Tt(r)=1407 s， θr=45.51°。打击距其关机点4666 km的目标。采用遗传工具箱进行优化，仿真参数见表1。

表1 仿真参数Tab.1 Parameters of simulation

4.2 仿真结果及设计方法有效性分析

基于上述参数设计多脉冲弹道并进行优化。取脉冲增量300 m/s、500 m/s例子进行分析，其优化结果如表2所示。对每一个速度增量，取优化成功30次中指标函数最小的那一组作为最优值输出。

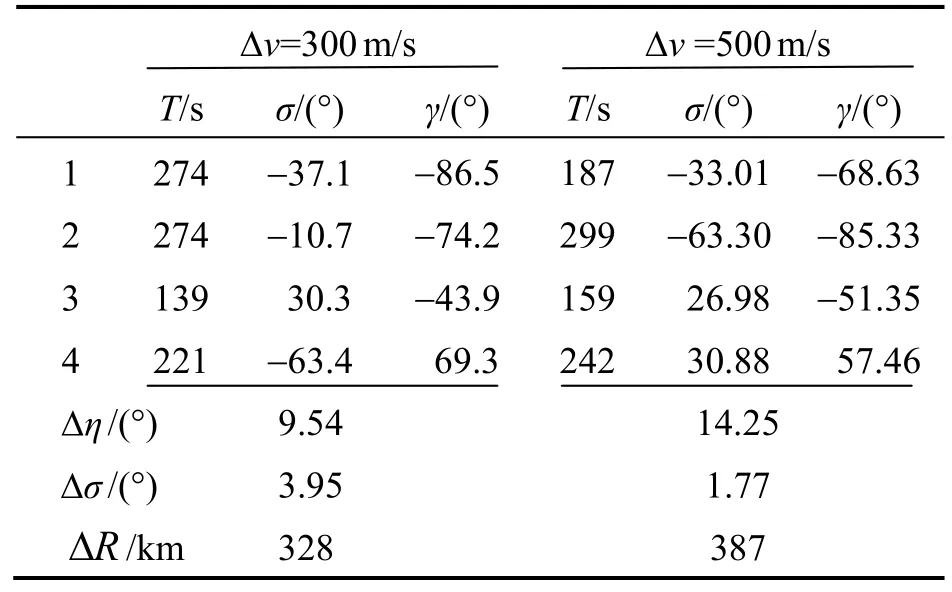
表2 优化结果Tab.2 Optimization results

导弹飞行轨迹如图4所示，从图中可以看出，由于脉冲的作用，弹道由5段异面弹道组成，点火前后弹道有很大差别。

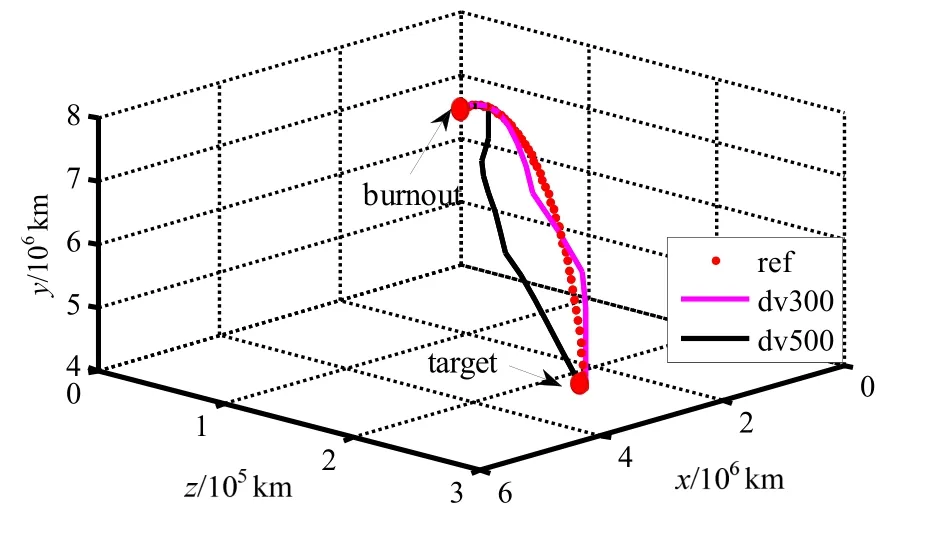
图4 多脉冲弹道轨迹图Fig.4 Multi-pulse ballistic trajectory

根据上面仿真结果，有如下结论：

1）敌方导弹防御系统根据点火前的弹道数据确定的落地点与点火后的落地点有很大区别。敌方防御系统必须重新采集导弹点火后的数据并确定其新的弹道。直到导弹最后一次点火结束，敌方才能确定其真实落点即敌方预警时间被大大缩短。

2）每段子弹道的飞行时间都小于τ，敌方无法完全确定导弹的弹道，导弹能够成功突防。导弹在脉冲点火变轨的同时也完成了弹道修正，使其逐步逼近直至最后击中目标。

综上所述，本文提出的弹道设计方法是有效的，且能同时满足导弹突防与打击精度的要求。

表3中例1为采用本文提出的设计方法得到的弹道。例2为采用文献[9]中的弹道设计方法得到的弹道。

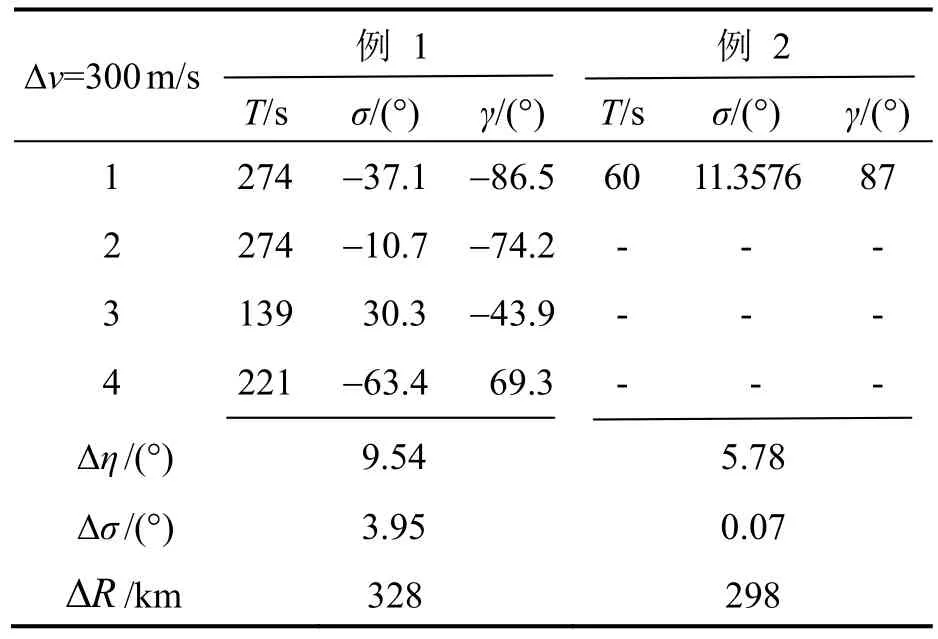
表3 对比结果Tab.3 Optimization results

例1中的弹道点火前后的平均距离为328 km。根据本文对 Ri的定义，Ri为真实导弹与“虚拟导弹”落地前的距离，所以点火前后弹道的落地点的平均距离要远大于328 km。例2中点火前后的弹道的落地点距离为298 km，小于例1中的弹道。在初始关机点，例1中Δη、Δθ比例2中大，说明例1的弹道对敌方更具有迷惑性，突防能力更强。这说明本文新提出的设计方法及评价函数是正确有效的。

文献[9]提出的设计方法需要通过指定中间弹道的落地点对求解方程组进行封闭，该值在可行解范围内随机选取，没有考虑变轨最优的问题。而本文提出的设计方法不仅不需要预先给定中间弹道的落地点，还从使敌方预测误差最大的角度对弹道进行了优化。因此，综合以上原因，本文建立的模型及提出的设计方法是有效的，且更加简洁方便，得到弹道的突防效果更好。

4.3 可行性、迭代效率及精度的分析

发动机比冲 ve=2500~3000 m/s，导弹的速度增量范围为100~500 m/s，根据齐奥尔科夫斯基火箭方程：

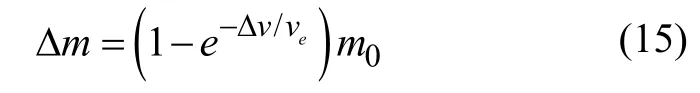
式中： m0为每次点火前导弹的质量， Δm 为每次点火消耗的质量。当 ve= 3000m/s 时，每次脉冲消耗燃料占点火前的弹头总质量的3.28%~15.35%，四次点火消耗燃料质量约占初始弹头总质量的12.80%~55.01%，五次点火为15.975%~68.31%。

以上分析说明本文采用四次脉冲点火的突防方法在工程上是可行的。

为了验证模型可行性及弹道设计方法的效率与迭代精度，将本文采用的方法（下文称为case1）与笛卡尔坐标下的数值积分方法[6]（下文称为case2）作对比。表4为计算结果的统计情况。

图5表示两者之间的迭代效率曲线，纵坐标表示非线性约束，横坐标表示迭代时间。可以看出，case1迭代效率远远高于case2。根据图6可以看出，case2的全局最优解大于case1的全局最优解。但是在将两者迭代100次后，选取优化指标最小的一组，两者大小接近。

表4 优化结果对比Tab.4 Planning contrast to the situation

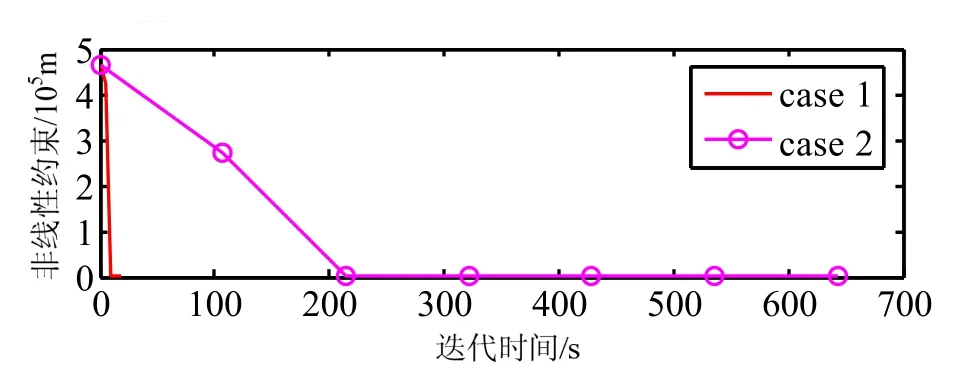
图5 迭代效率Fig.5 Iterative design process efficiency

图6 预测误差随迭代变化情况Fig.6 Prediction error with iterative changes

通过上述对比与分析，说明本文建立的多脉冲点火模型是可行的，提出的弹道设计方法是有效的，且在工程上都是能实现的。此外，设计优化时间不到20 s，说明设计优化一条弹道耗时短。该方法可以根据瞬息变化的战场情况，做出有针对性的快速反应。

5 结 论

本文研究了弹道导弹中段多脉冲突防弹道的设计问题，建立了新的脉冲点火模型，提出了新的设计方法与评价函数。结论如下：

1）将弹道设计问题转化成路径规划问题的方法是可行的。以此为基础建立的多脉冲点火模型、提出的弹道设计方法及评价体系是简单有效的。设计出的弹道可以有效地迷惑敌方防御系统，缩短其预警时间。其采用逐步逼近法，在机动变轨同时完成弹道修正，保证了导弹的打击精度。

2）该设计方法在 20 s内设计出一条中段突防弹道。可以根据最新的情报信息迅速做出反应，规划一条突防概率最大的弹道。设计方法具有很高的灵活性，很难被敌方反制。

（References）：

[1] Corbett M. A new approach to ballistic missile defense for countering antiaccess/area-denial threats from precision guided weapons[J]. Air & Power Journal, 2013: 83-106.

[2] Qihang Z, Cheng D, Qifan Z, et al. The trajectory of anti-ship ballistic missile design and simulation [C]//2015 Fifth International Conference on Instrumentation and Measurement, Computer, Communication and Control. IEEE, 2015: 373-377.

[3] Gao M, Zhang Y, Yang S. Firing control optimization of impulse thrusters for trajectory correction projectiles[J]. International Journal of Aerospace Engineering, 2015: 1-11.

[4] Gao M, Zhang Y, Yang S, et al. Trajectory correction capability modeling of the guided projectiles with impulse thrusters[J]. Engineering Letters, 2016, 24(1): 7-19.

[5] Druckmann E, Ben-Asher J Z. Optimal in-flight trajectory modifications for ballistic missiles and free rockets [J]. Journal of Guidance, Control, and Dynamics, 2012, 35(2): 462-470.

[6] 夏红伟, 李秋实, 李莉, 等. 基于hp自适应伪谱法的飞行器再入轨迹优化与制导[J]. 中国惯性技术学报, 2015, 23(6): 818-823. Xia H W, Li Q S, Li L, et al. Trajectory optimization and guidance for reentry craft based on hp-adaptive pseudospectral method[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 818-823.

[7] Guo Y, Yao Y, Wang S, et al. Maneuver control strategies to maximize prediction errors in ballistic middle phase[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(4): 1225-1234.

[8] Guo Y, Yao Y, Wang S ,et al. Maneuver strategy of evader considering detection system[C]//AIAA Guidance, Navigation, and Control Conference. Portland, Oregon, 2011: 143-156.

[9] 张广明, 高普云, 唐乾刚. 弹道导弹在被动段突防的脉冲式异面变轨方法[J]. 宇航学报, 2008, 29(1): 89-94. Zhang G, Gao P, Tang Q. The method of the impulse trajectory transfer in a different plane for the ballistic missile penetrating missile defense system in the passive ballistic curve[J]. Journal of Astronautics, 2008, 29(1): 89-94.

[10] 高普云, 张广明, 冯志刚, 等. 基于脉冲点火弹头空间机动的被动段弹道设计方法和数值仿真[J]. 宇航学报, 2009, 30(3): 884-889. Gao P, Zhang G, Feng Z, et al. The method of the trajectory design and numerical stimulation of the missile maneuvers in space based on the impulse firing in the passive curve[J]. Journal of Astronautics, 2009, 30(3): 884-889.

Penetration trajectory design based on defense system delay and maximum prediction errors in ballistic midcourse

QI Nai-ming1, ZHOU Qi-hang1,2, CUI Nai-gang1, DONG Cheng1,3
(1. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China; 2. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China; 3. Beijing Aerospace Xin Feng Machinery Equipment Limited Liability Company, Beijing 100854, China)

This paper investigates the midcourse maneuver penetration trajectory design of ballistic missile, which is converted into path planning for simplification, and whose principle and method are different from the widely used ones. Considering the delay of the enemy’s defense system, a multi-pulse ignition model is developed, and the parameters of the burnout are designed and optimized based on the idea of the changeable launching plane. Then a developed evaluation function is adopted to maximize the prediction error of the enemy. The trajectories are further optimized by using the genetic algorithm. Meanwhile, a method of multi-pulse trajectory design is given, which satisfy the penetration and accuracy. The model, design and evaluation methods are verified through simulation from the aspects of feasibility, validity, flexibility, efficiency and precision. The PC simulation shows that an effective trajectory can be designed within 20 s, and this method is effective and efficient.

multi-pulse; prediction errors; system delay; changeable launching plane; maneuvering penetration

V412.1

：A

2016-01-25；

：2016-04-22

上海航天科技创新基金（SAST201312）

齐乃明（1962—），男，教授，博士生导师，主要研究航天器飞行动力学控制与仿真、地面半实物仿真技术研究、月球车系统设计与自主制导导航控制技术等三个领域。E-mail: zhou0204022@126.com

1005-6734(2016)03-0409-06

10.13695/j.cnki.12-1222/o3.2016.03.024