基于模式能量流法的互联电网功率振荡能量解析与主振荡路径识别

刘 铖，蔡国伟，杨德友，孙正龙

基于模式能量流法的互联电网功率振荡能量解析与主振荡路径识别

刘 铖1，蔡国伟2，杨德友2，孙正龙2

(1.华北电力大学电气与电子工程学院, 北京 102206；2.东北电力大学电气工程学院，吉林 吉林 132012)

针对互联电力系统的功率振荡现象，为了能够深入剖析，构建了模式能量流函数，对互联电力系统的功率振荡进行网络模式能量的求取，并进行能量解析。在此基础上，利用所建立的基于广域量测信息的模式阵型指标，判别系统功率振荡发电机分群情况，同时根据所建立的主振荡路径判别指标对系统主振荡路径进行辨识，得到系统能量交互的主振荡路径。通过对4机两区和8机36节点算例进行仿真，验证了所提出的互联电力系统功率振荡能量解析与主振荡路径识别方法的有效性。

互联电力系统；功率振荡；主振荡路径；模式能量解析；矩阵束

0 引言

功率振荡是现代大型互联电网稳定运行主要威胁之一。系统中某处的扰动通常会波及到离故障地点很远的区域，引起系统中大量元件动态运动，发生功率振荡。为此需要研究互联电网功率振荡的物理本质及传播功率[1-8]。

目前学者们已从多个角度对互联电网功率振荡引起的因素和机理进行了研究[1-6]，研究方法主要有以特征值分析法、频域分析法[1]等为代表的线性分析方法、以时域仿真法为代表的非线性分析方法、基于信号的方法[6]等。但是这些方法都具有一定局限性，适用环境和揭示问题有限，不能全面揭示功率振荡信息，针对功率振荡过程中存在的两个关键问题：

1) 哪些机组发生振荡，机组参与程度如何；

2) 振荡主要传播路径如何。

现有很多方法仍未较好解决上述问题。能量函数法在暂稳领域得到了广泛的应用[9-10]，但在功率振荡上应用尚属起步阶段。学者们从能量角度分析低频振荡正成为热点，且已取得一定成果[11-14]。目前基于能量函数法低频振荡分析主要根据能量函数进行强迫功率振荡扰动源辨识[11-14]，取得了较好效果，但是研究仅针对强迫功率振荡问题，对较为普遍的弱、负阻尼引起的功率振荡现象并未很好揭示。

此外，互联电网中不同因素引起的功率振荡，振荡模式与各发电机参与程度不一，文献[15]利用模式动能表征发电机参与程度，但未揭示能量在网络中的传播过程，而主振荡传播途径在不同振荡模式下差别可能非常显著，并且找到主振荡路径能够获得更为详细的能量交互过程。这表明，有效选择能量传播路径是十分重要的问题。

当大规模电网受到扰动发生功率振荡，现今抑制功率振荡的方式多数从振荡源头(发电机组或负荷)，又或者在联络线上施加控制，确实起到对功率振荡的抑制效果；但是在抑制过程中，也可能激发其他新一轮振荡事故。若找到低频振荡过程中的主振荡路径，并基于该路径制定合适的控制策略，就能快速并有效地抑制功率振荡。

目前只有少数学者研究低频振荡的路径辨识问题，如文献[16]已经证实存在主路径，但其辨别主振荡路径主要应用电压、电流灵敏度方法，不足处在于计算较为复杂。为此，针对上述方法不足，本文从全新角度揭示互联电网功率振荡的本质，建立了基于广域量测信息的模式能量流函数，得到全网各支路的模式能量分布，对全网进行能量解析，同时通过建立的主振荡路径指标得到系统能量交互的主振荡路径。所提方法可揭示功率振荡过程中的能量交互情况和主路径，相比传统主路径识别方法，获得信息丰富，且直观准确。所提方法的有效性通过算例仿真得以验证。

1 基于振荡能量流的互联电网功率振荡能量解析

1.1 功率振荡的传播路径

互联电网发生功率振荡时，不同区域的能量交换对象(发电机，输电线路，控制器等)在振荡过程中进行能量交换，存在能量交互通道[15]。在不同的振荡模式下，能量交互路径不同，但其振荡路径，包含该模式的丰富信息，尤其对于区间模式，其振荡频率低，影响范围广泛，可以考虑把该模式下的振荡通道作为主振荡路径，即区间模式下不同元件间进行能量交互的主要通道就是需要重视的主振荡路径[15]。

振荡路径中含有丰富的模式信息，而且客观性好，如果能够得到系统的主振荡路径，对电网的能量流动解析和功率振荡抑制具有重要意义。

1.2 模式振荡能量流函数

根据功率振荡相关理论，通过计算全网支路势能变化及分布，实现互联电网的能量解析，功率振荡下电网的支路势能函数为[6]

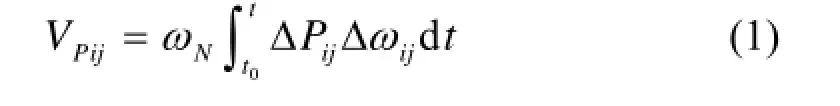
由式(1)可知，电网支路势能是全网势能总的外在表现，通过该式计算的势能是各种模式能量的综合表现，虽然该势能函数体现系统振荡时的能量分布，但不能有效获得系统网络振荡在各个模式下的能量分布信息，难以利用传统支路势能进行模式阵型确定与主振荡路径辨识。

在小扰动下，由于电网中电气量可用各个模式线性叠加表示，同时难以通过解析表达式获得网络量的模式表示，所以为了解决上述难题，本文在前人研究基础上[9,15-16]，利用矩阵束理论对表征功率振荡过程较为明显的两个电气量，即线路功率Pij或线路角频率差ijw进行辨识，提取功率振荡的不同模式分量，如式(2)、式(3)所示。

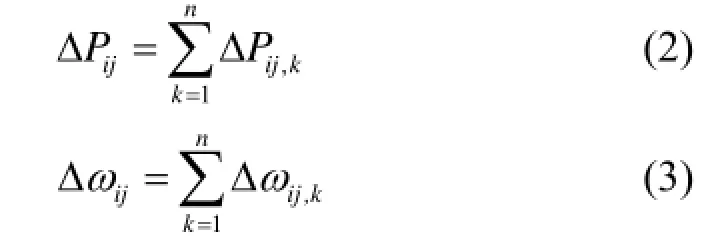
式中，n为小扰动下不同模式成分个数。

对不同模式成分分别建立对应模式成分的网络支路势能函数，实现不同模式下的能量解析，交互模式成分一般成分较小，不作考虑，只考虑对应项频率成分，定义各支路模式振荡能量流函数如式(4)所示。

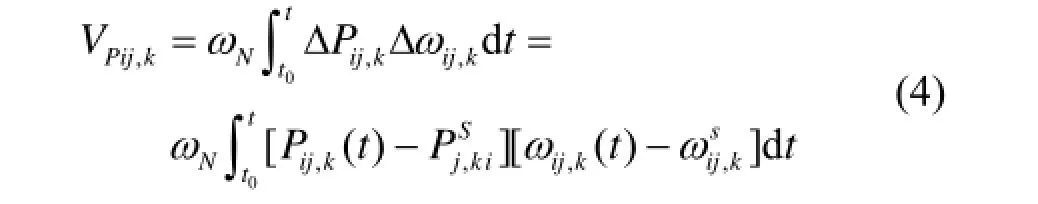
式中：Pij,k为模式k下线路Li-j的有功功率；为模式k的线路Li-j有功功率的稳态值；为模式k下的线路Li-j两端的角频率差；为模式k下的线路Li-j两端的角频率差的稳态值。

通过对广域量测获取的网络线路功率和线路角频率差信号进行矩阵束辨识，并计算得到不同模式下的能量流分布，借此可对互联电网功率振荡进行能量解析，该支路的能量函数包括电网的模式信息，可以有助于揭示系统功率振荡下的能量交互本质。

2 互联电网功率振荡的主振荡路径辨识

2.1 互联电网功率振荡主振荡路径指标计算

互联电网发生功率振荡，不同机群间能量具有交互转换关系，以两群振荡为例，能量在两群通过主要通道进行能量交互。

根据1.2节建立的模式振荡能量函数，可以求出不同模式的网络能量分布，以此为基础，定义模式阵型指标(Mode shape index, MSI)为

式中，Vp,k,i为模式k下各支路i的振荡能量。互联系统发生功率振荡，呈现两群振荡的两部分支路MSI指标正负相反。可根据式(5)的MSI指标正负进行分群，说明两群发电机之间进行功率振荡。根据MSI指标可判定系统功率振荡阵型情况并确定振荡的区域。

此外，由于发电机出口支路势能与发电机动能能量交换显著，可用发电机出口支路的势能表征各发电机参与振荡的程度。所以为了能够表征系统功率振荡过程中各发电机的参与振荡程度，类比小干扰分析中参与因子的作用，定义发电机参与度评价指标(participation factor index，PFI)为

式中， Vp,k,i为模式k下发电机各支路j的振荡能量。可见，参与度指标是根据发电机出口支路的模式能量指标大小进行评价。

本文将振荡的两群机组内交互能量最为剧烈的两台发电机之间的连接线路作为主振荡路径，对主路径的辨识可以有效地揭示能量交互本质，且可为基于网络的阻尼控制提供理论依据。

下面定义主振荡路径判别指标(main oscillation path index, MOPI)为

根据MOPI大小排序，同时结合是否构成连接闭合路径确定主振荡路径。

2.2 功率振荡主振荡路径识别的实现方法及步骤

2.2.1 矩阵束算法

对任意时刻含噪平稳振动信号为

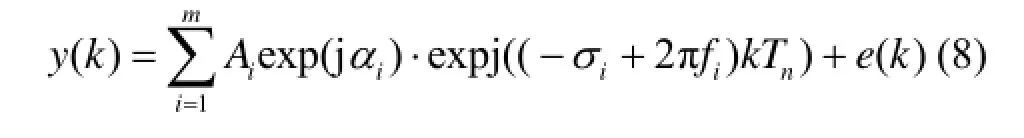
则：

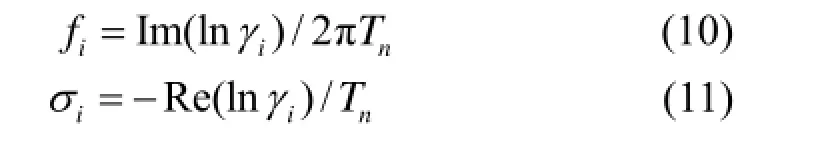
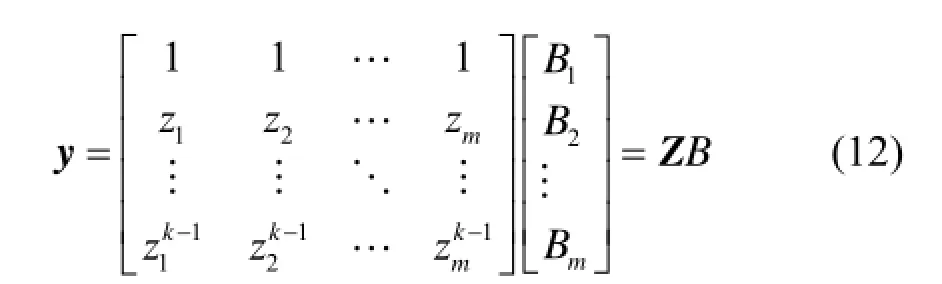
通过最小二乘法求解：

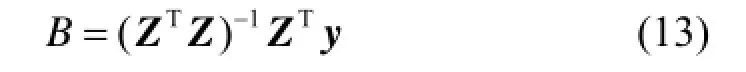
得到各振动分量的振幅和相位。

2.2.2 主振荡路径定位的计算步骤

准确识别功率振荡临界机群是判断功率振荡主振荡路径的前提条件。基于上述所提指标，说明基于网络能量的主振荡路径辨识步骤。主振荡路径的识别步骤如下：

1) 首先，量测网络各支路有功功率和线路两端角频率差。

2) 利用矩阵束辨识各支路 Lij的有功功率和线路两端角频率差的各模式成分，获取线路 Lij各机电模式的和

模式变化量。

3) 求取线路Lij的能量，可得到不同模式的全网能量分布，对全网能量解析，也可对关心模式进行能量分布获取。

4) 计算MSI判别功率振荡阵型，计算PFI判断不同振荡区域各发电机参与度，确定各自区域临界发电机，最后计算MOPI，且对MOPI绝对值从大到小排序。

5) 根据 MOPI的排序结果，依次添加 MOPI绝对值大的支路，直到系统是连通图，那么该路径就是主振荡路径；如果系统依旧是非连通图，那么依次从大到小添加支路，直至系统成为连通图。

通过本文建立的基于MOPI的功率振荡主振荡路径辨识方案，可以快速寻找到主振荡路径。

3 算例分析

3.1 四机两区系统算例

以四机两区域算例系统为例[13]，如图1。

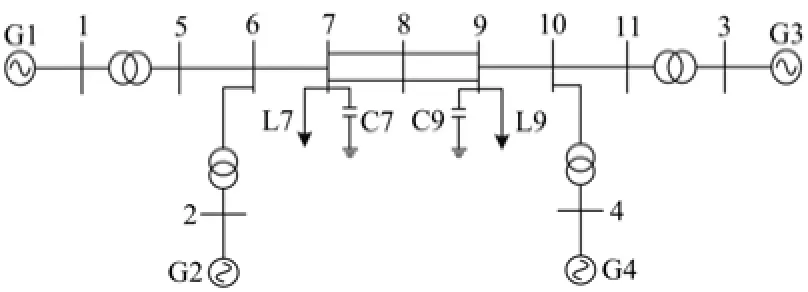
图1 四机两区系统图Fig. 1 4 machine 2-areas system

为深入分析本文提出的功率振荡主振荡路径辨识方案的有效性，下面对不同模式能量分布及主振荡路径进行研究。根据表1的小干扰结果，模式1为区间模式。首先通过传统能量函数法可得到各支路势能分布如图2所示。

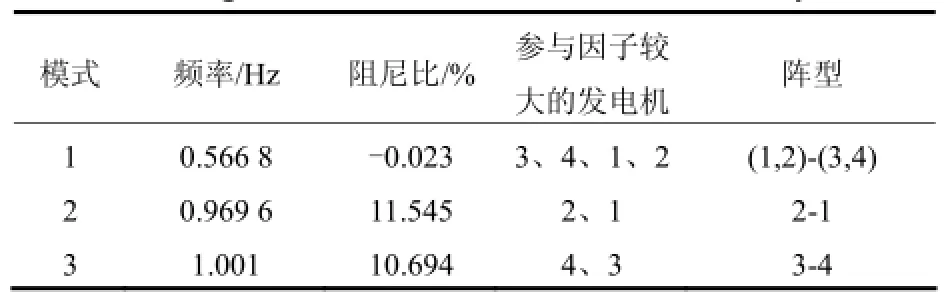
表1 4机算例特征值计算结果Table 1 Eigenvalue results of 4-machine 2-area system

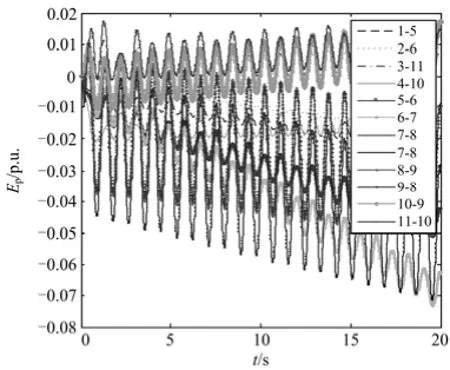
图2 传统能量函数法得到的各支路势能曲线Fig. 2 Each branch potential energy curves obtained by traditional energy function method

可知，传统方法系统各支路势能分布规律不明显，难以区分振荡机群及各发电机参与程度。

采用本文算法可得模式1能量流如图3所示。可知，模式 1下各支路的能量流明显分成正负两群，G1，G2与G3、G4进行能量交换，与该模式下小干扰所得区域间模式1的0.566 8 Hz阵型一致。

可见本文方法能得到不同模式下的模式能量流分布图，可分层了解不同模式下的能量振荡情况，对网络振荡进行解析，同时由图3所示的区间模式能量分布可知，在整个振荡过程中模式1的区间振荡模式始终振幅较大，为主导振荡模式。

图3 模式1的能量流分布Fig. 3 Energy distribution under mode 1

此外，计算模式1的MSI，如图4所示。 可知，通过MSI可得到系统阵型，与模式1的小干扰结果及能量分布一致。在判别振荡能量交互模式后，计算MOPI，如表2所示。首先通过MSI可知，系统为两群振荡模式，发电机出口支路PFI可表征发电机的参与因子，比较4个发电机支路PFI大小，可知G1、G3分别为区域1和2中参与因子较大的发电机。系统在 G1与 G3间振荡较为剧烈，根据MOPI大小排序，同时连接相关支路可知整个系统的主振荡路径如图5所示，G1与G3振荡交互能量，且是两区域中参与因子大的两台机。

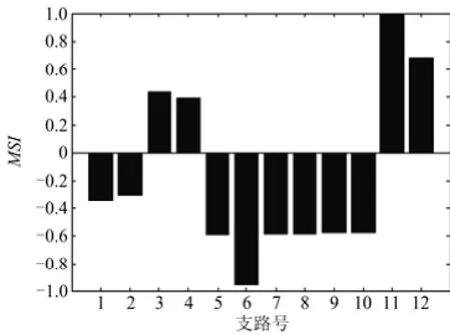
图4 模式1的各支路MSIFig. 4 MSI of each branch under mode 1

3.2 8机系统算例

以8机算例系统为例如图6，通过本文方法计算支路模式能量，本文列举其中两个模式如图7、图8所示。

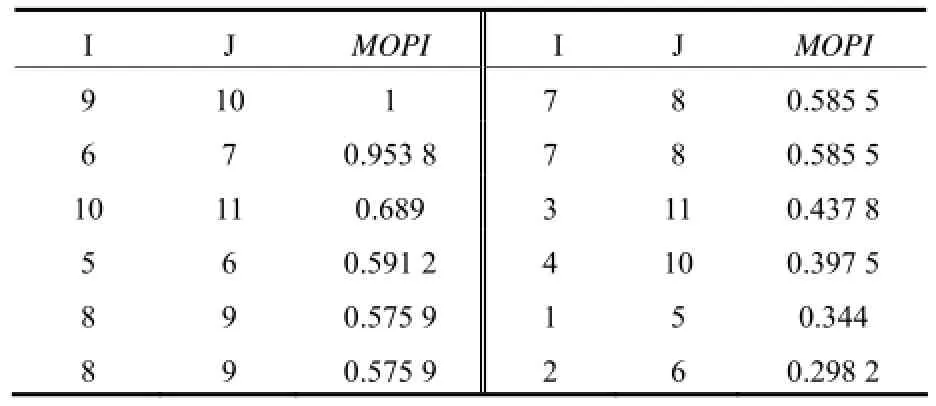
表2 四机系统MOPI计算结果Table 2 MOPI calculation results of 4-machine system

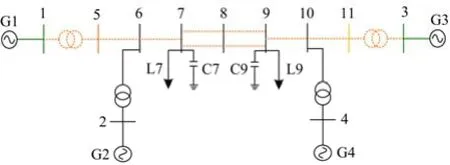
图5 四机系统的主振荡路径Fig. 5 Main oscillation path of four machine system

可知模式 1、2的模式能量流分布情况与表 3所示阵型一致。同时MSI指标如图9所示，所得结果与表 3所示特征根结果一致。根据图 9和图 10所示MSI正负可知，模式1与模式2下系统呈现两群振荡。

由图 11可知，G1与 G3振荡并进行能量交换，由小干扰及MSI结果可知两者均是各自区域参与因子较大的发电机。所以振荡主要发生在G1和G3之间，两者间所连路径即为模式1的振荡路径。

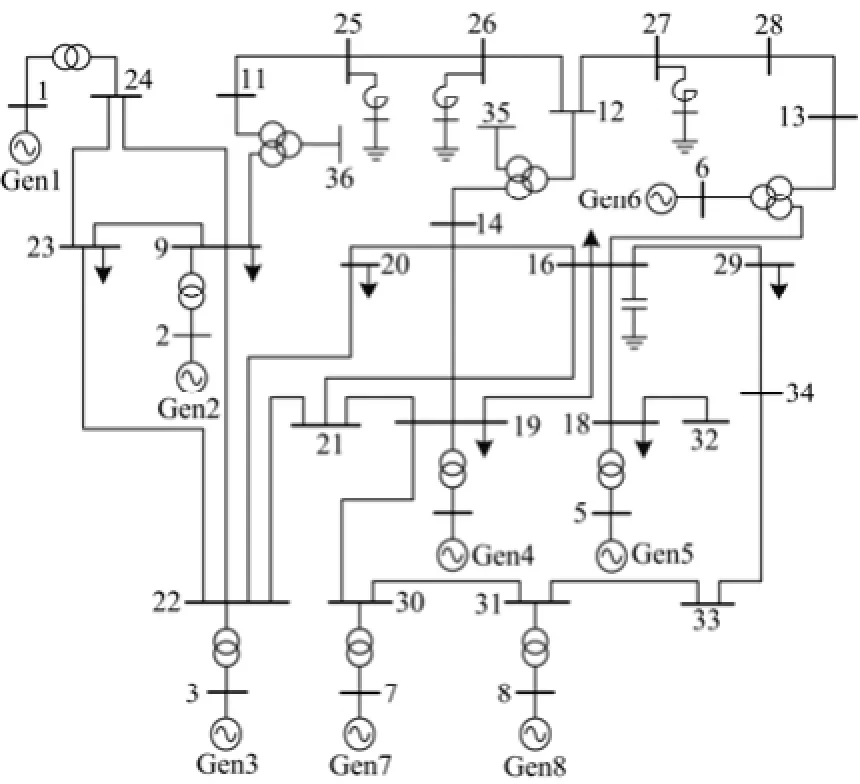
图6 8机系统图Fig. 6 8 machine system

图7 模式1的能量流分布Fig. 7 Energy distribution under mode 1

表3 8机特征值计算结果Table 3 Eigenvalue calculation results of 8-machine system

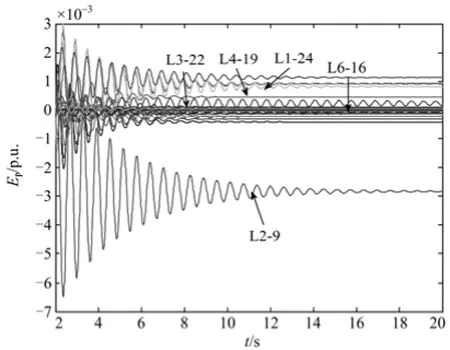
图8 模式2的能量流分布Fig. 8 Energy distribution under mode 2

根据表4所示的模式1的MOPI指标可知，系统模式1的路径如图11所示。

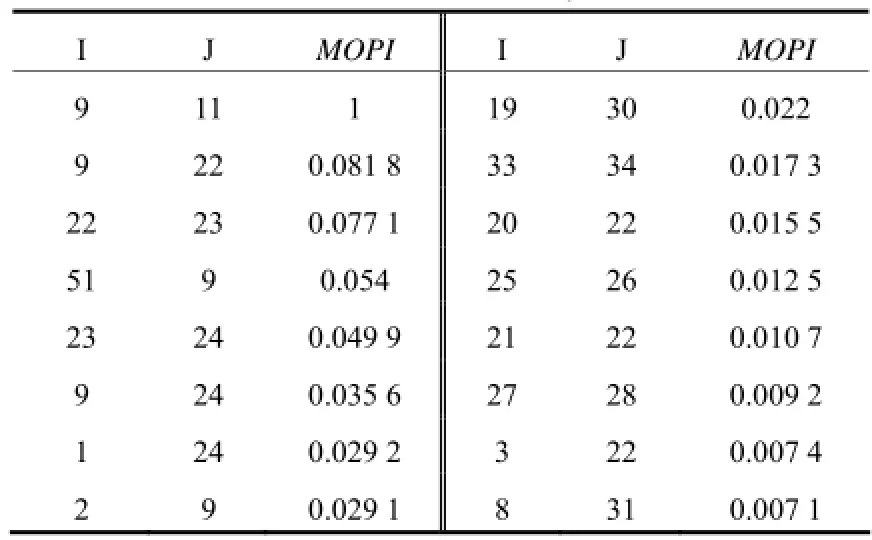
表4 8机模式1的MOPI计算结果Table 4 MOPI results of 8-machine system under mode 1

图9 模式1的MSI指标Fig. 9 MSI of each branch under mode 1

同理，根据如表5所示的模式2的MOPI指标，可以得到模式2的主振荡路径如图12。

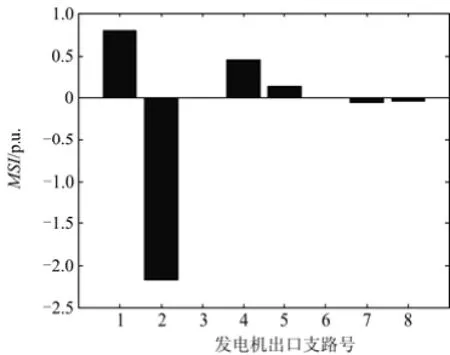
图10 模式2的MSI指标Fig. 10 MSI of each branch under mode 1

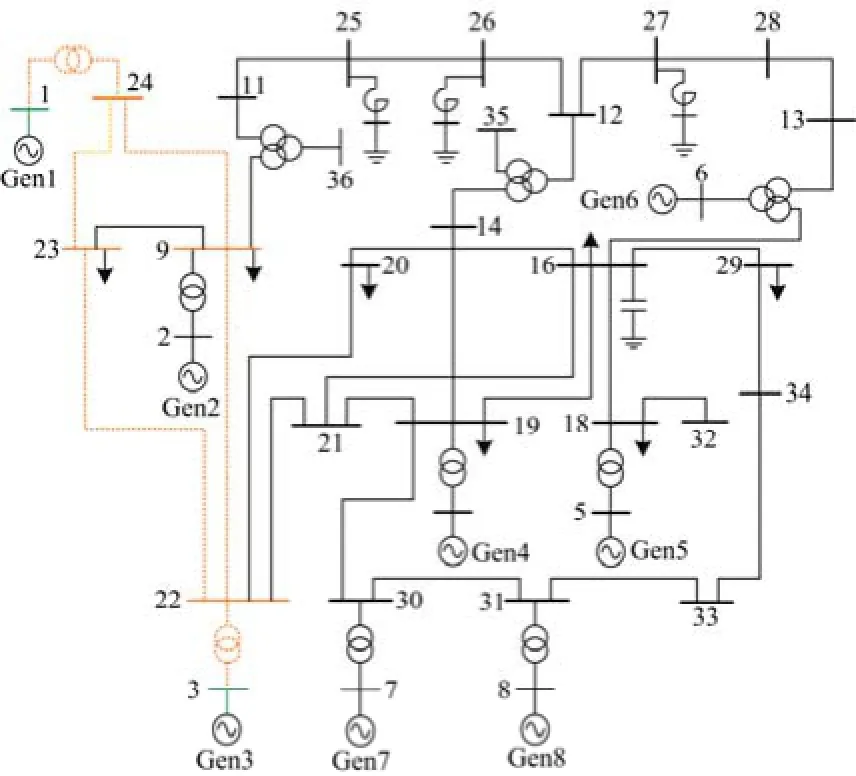
图11 模式1的振荡路径Fig. 11 Main oscillation path of mode 1

可见振荡主要发生在G2与G1间。模式2下系统振荡能量主要通过G1和G2间主振荡路径进行能量交换，G1与G2分别是振荡两群内参与度较大的发电机，且该振荡对应模式2的本地振荡。观察不同模式能量可知模式1模式能量较为明显，呈现主导振荡趋势，所以模式1的振荡路径为该运方下的主振荡路径，可见本文方法可以有效从广域量测数据对功率振荡进行能量解析与路径辨识。

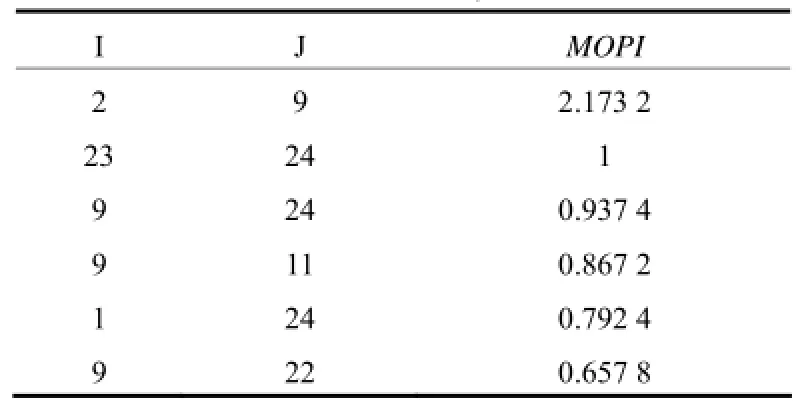
表5 8机模式2的MOPI计算结果Table 5 MOPI of 8-machine system under mode 2

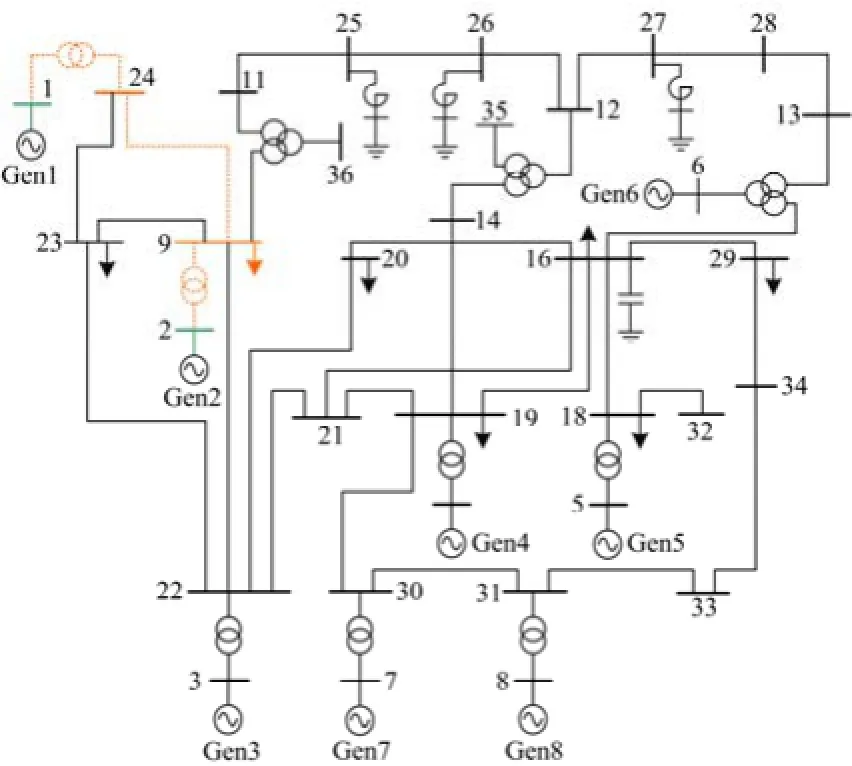
图12 模式2的振荡路径Fig. 12 Main oscillation path of mode 2

4 结论

本文通过求取基于网络的广域量测模式能量流，对互联电网功率振荡进行模式能量解析，可得到系统功率振荡的振荡交互阵型，同时通过建立的MSI指标可快速判别功率振荡阵型及各发电机参与度，本文方法得到的振荡模式是从能量角度分析得到，更为细致地揭示系统振荡本质，显示也较传统方法更为直观，在此基础上，利用MOPI

指标可判别系统主导振荡路径，进一步揭示系统功率振荡的能量交互通道，这部分内容可为后续基于网络的阻尼控制的反馈信号选取、控制器选址和设计提供理论依据。

[1] 耿天翔, 张竹竞, 项丽, 等. 基于起振特性的强迫振荡扰动源定位及解列方案[J]. 电力系统保护与控制,2015, 43(6): 98-103.

GENG Tianxiang, ZHANG Zhujing, XIANG Li, et al. A locating and splitting scheme for disturbance source of forced power oscillation based on the propagation characteristic[J]. Power System Protection and Control, 2015, 43(6): 98-103.

[2] 李阳海, 黄莹, 刘巨, 等. 基于阻尼转矩分析的电力系统低频振荡源定位[J]. 电力系统保护与控制, 2015, 43(14): 84-91.

LI Yanghai, HUANG Ying, LIU Ju, et al. Power system oscillation source location based on damping torque analysis[J]. Power System Protection and Control, 2015, 43(14): 84-91.

[3] 姚致清, 张茜, 刘喜梅. 基于 PSCAD/EMTDC的三相光伏并网发电系统仿真研究[J]. 电力系统保护与控制, 2010, 38(17): 76-81.

YAO Zhiqing, ZHANG Qian, LIU Ximei. Research on simulation of a three-phase grid-connected photovoltaic generation system based on PSCAD/EMTDC[J]. Proceedings of the CSEE, 2010, 38(17): 76-81.

[4] 赵红生, 刘源, 陈伟彪, 等. 互联电力系统联络线功率波动机理及其扰动概率分析[J]. 电力系统保护与控制, 2015, 43(14): 1-9.

ZHAO Hongsheng, LIU Yuan, CHEN Weibiao, et al. Fluctuation mechanism of tie-line active power of interconnected power system and its oscillation probability analysis[J]. Power System Protection and Control, 2015, 43(14): 1-9.

[5] HAO Zhenghang, YAO Zhiqing, LI Shaohua, et al. The contribution of double-fed wind farms to transient voltage and damping of power grids[J]. Tehnicki Vjesnik, 2015, 22(1): 43-49.

[6] 赵妍, 李志民, 李天云. 电力系统低频振荡监测的Duffing振子可停振动系统法[J]. 电工技术学报, 2015, 30(20): 159-167.

ZHAO Yan, LI Zhimin, LI Tianyun. Duffing oscillator order stopping oscillation system method for monitoring of low-frequency oscillation in power system[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 159-167.

[7] 李从善, 刘天琪, 刘利兵, 等. 直流多落点系统自抗扰附加阻尼控制[J]. 电工技术学报, 2015, 30(7): 10-17.

LI Congshan, LIU Tianqi, LIU Libing, et al. An auto-disturbance rejection controller of multi-HVDC[J]. Transactions of China Electrotechnical Society, 2015, 30(7): 10-17.

[8] 陈恩泽, 刘涤尘, 廖清芬, 等. 多重扰动下的跨区电网低频振荡研究[J]. 电工技术学报, 2014, 29(2): 290-296.

CHEN Enze, LIU Dichen, LIAO Qingfen, et al. Research on low frequency oscillation of interconnected power grid based on multiple disturbances[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 290-296.

[9] 蔡国伟, 穆钢, CHAN K W, 等. 基于网络信息的暂态稳定性定量分析—支路势能法[J]. 中国电机工程学报, 2004, 24(5): 2-5.

CAI Guowei, MU Gang, CHAN K W, et al. Branch potential energy method for power system transient stability assessment based on network dynamic variables[J]. Proceedings of the CSEE, 2004, 24(5): 2-5.

[10] PAI M A. Energy function analysis for power system stability[M]. Boston, MA: Kluwer, 1989: 20-35.

[11] 李颖, 沈沉, 刘锋, 等. 基于Hamilton实现的电力系统振荡源设备级定位[J]. 电力系统自化, 2012, 36(23): 6-11.

LI Ying, SHEN Chen, LIU Feng, et al. Oscillation source location in control devices of generators based on Hamilton realization[J]. Automation of Electric Power Systems, 2102, 36(23): 6-11.

[12] 余一平, 闵勇, 陈磊, 等. 基于能量函数的强迫功率振荡扰动源定位[J]. 电力系统自动化, 2010, 34(5): 1-6.

YU Yiping, MIN Yong, CHEN Lei, et al. Disturbance source location of forced power oscillation using energy function[J]. Automation of Electric Power Systems, 2010, 34(5): 1-6.

[13] CHEN Lei, MIN Yong, HU Wei. An energy-based method for location of power system oscillation source[J]. IEEE Transactions on Power Systems, 2012, 28(2): 828-836.

[14] 李颖, 沈沉, 刘锋, 等. 基于Hamilton实现的电力系统振荡源设备级定位[J]. 电力系统自动化, 2012, 36(23): 6-11.

LI Ying, SHEN Chen, LIU Feng, et al. Oscillation source location in control devices of generators based on Hamilton realization[J]. Automation of Electric Power Systems, 2102, 36(23): 6-11.

[15] JING C, MACALLEY J D, KOMMATEDDY M. An energy approach to analysis of inter-area oscillation on power system[J]. IEEE Transactions on Power Systems, 1996, 11(2): 734-740.

[16] CHOMPOOBUTRGOOL Y, VANFRETTI L. Identification of power system dominant inter-area oscillation paths[J]. IEEE Transactions on Power Systems, 2012, 28(3): 1-10.

[17] HUA Y B, SARKAR T K. Matrix pencil method for estimating parameters of exponentially damped sinusoids in noise[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1990, 38(5): 814-824.

(编辑 周金梅)

Power oscillation energy analysis and the main oscillation path identification of interconnected power systems based on the mode energy flow

LIU Cheng1, CAI Guowei2, YANG Deyou2, SUN Zhenglong2
(1. School of Electrical Engineering, North China Electric Power University, Beijing 102206, China; 2. School of Electrical Engineering, Northeast Dianli University, Jilin 132012, China)

As to power oscillation phenomenon of the interconnected power systems can be further revealed, mode energy flow function is proposed. Then network mode energy is calculated, and the power oscillation of interconnected power grid is analyzed by oscillation energy. Thus, mode shape index based on the wide-area measurement information is constructed to judge power oscillation generator groups. At the same time, the main oscillation path index of power system is set up to identify main oscillation path, and in order to get the energy interaction main oscillation path. Through simulation of four machine two area and 8-machine 36 node examples, the effectiveness of proposed power oscillation energy analysis and the main oscillation path identification method is validated. This work is supported by National Natural Science Foundation of China (No. 51377017).

interconnected power grid; power oscillation; main oscillation path; mode energy analysis; matrix pencil

2015-11-18；

2016-01-03

刘 铖(1985-)，男，通信作者，博士研究生，助教，研究方向为电力系统稳定分析与控制；E-mail: 05dylc@ 163.com

蔡国伟(1968-)，男，博士，教授，研究方向为电力系统稳定分析与控制；

杨德友(1983-)，男，博士，研究方向为电力系统稳定分析与控制。

10.7667/PSPC152013

国家自然科学基金资助项目(51377017)；国家电网公司大电网重大专项资助项目(SGCC-MPLG012-2012)