一种基于智能改进算法的定制电力设备优化配置策略

冯兴田，孙添添，马文忠

一种基于智能改进算法的定制电力设备优化配置策略

冯兴田，孙添添，马文忠

(中国石油大学(华东)信息与控制工程学院，山东 青岛 266580)

为了更好地治理配电网谐波污染、低功率因数以及电力系统电压波动所带来的敏感负荷不能正常工作问题，研究了配电网多种定制电力设备的优化配置。综合考虑电能质量治理目标以及投资费用建立了优化配置数学模型，并提出一种将遗传算法与内点法有机结合的混合优化策略用于多种定制电力设备的优化配置。该混合策略利用遗传算法锁定各装置的最优安装位置并求得近似最优安装容量，将近似容量设为内点法初值寻找更加精确更优的安装容量。此外，分别基于约束越限和预判自适应对遗传算法和内点法做出改进，提高了寻优速度。理论分析和仿真结果表明，该混合算法比单独的遗传算法稳定性更高、寻优结果更加精确。

遗传算法；内点法；优化配置；电能质量；定制电力设备

0 引言

配电网在运行过程中存在各种各样的电能质量问题，诸如配电网谐波问题、电压的波动与闪变、低功率因数等等。既影响用户设备的正常运行，加大供电端负担，又会对公用电网造成污染。定制电力设备能够经济有效地改善电能质量问题，目前已得到广泛应用。有源滤波器(APF)、配电网静止同步补偿器(D-STATCOM)和动态电压恢复器(DVR)是目前研究技术成熟、实际应用中最为常见的配电系统定制电力设备[1-3]。在配电网中安装多种定制电力设备时，若能合理选择各装置的安装位置和容量既可保证电能质量达到相关要求，也能避免设备容量的浪费，减少投资成本。

在电能质量改善装置的选型及定容定址问题上，运用较多的是遗传算法、免疫算法等智能算法[4-10]。例如，文献[4-5]利用遗传算法对输电网中多种电能质量补偿装置进行了优化配置，提高了输电系统的带载能力并节约了投资成本。文献[6]利用遗传算法研究了多台动态电压恢复器在配电网的优化配置问题，实现了配电网中多台不同电压等级的DVR的优化配置。文献[7]利用免疫算法对配电网中的无源滤波器进行了优化配置，与遗传算法相比可以避免陷入局部最优。文献[8]采用了一种基于变焦佳点集和种群熵的改进多目标引力搜索优化算法对柔性输电设备的位置及容量组合进行优化配置，取得了不错的效果。但是智能算法虽然有其特有的优势，如鲁棒性强，易于处理非线性、离散问题，但在求解精确度上却没有传统数值算法高[9-11]。另外，内点法因为存在无法处理离散变量、对初始点的要求高等缺陷而无法在此类优化配置问题上单独使用。因此将智能算法与传统非线性规划方法融合，结合各自优势并互补不足，理论上可以取得优于智能算法的效果。

本文提出一种将遗传算法与内点法有机结合的混合改进算法处理定制电力设备的优化配置问题。首先，利用遗传算法同时处理配置问题中的离散变量和连续变量，得各装置最优安装位置和容量。将所求安装位置锁定，设备参数输出作为内点法初值，运用内点法对安装容量这一连续变量做进一步寻优。此外，本文遗传算法在随机赋值生成初始种群的基础上，根据约束是否越限加入扩展调整环节，提高了遗传算法在该优化配置问题的寻优速度；运用内点法时，提出一种基于预判迭代次数的自适应取值方法确定中心参数，一定程度上加速了内点法在本文优化配置的收敛速度，保证了所求结果的可行性。通过算例仿真，证明了该算法在定制电力设备优化配置问题上的可行性，与遗传算法相比，稳定性更高、寻优结果更加精确。

1 优化配置数学模型

本文优化配置主要针对APF、D-STATCOM和DVR三种典型定制电力设备。配电网多种定制电力设备的优化配置是一个多变量、多约束的非线性规划问题[12]。数学模型可以表示为

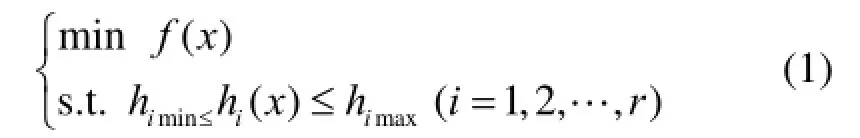
式中：x是一组包括 APF参数、DVR参数以及D-STATCOM参数的N维列向量；r为不等约束个数。目标函数f (x)为初期新增设备总投资最小。

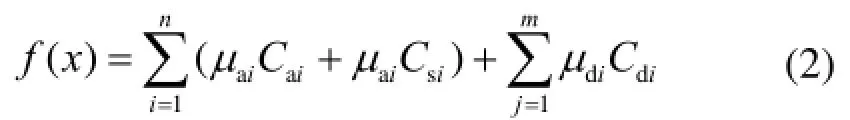
式中：n为配电网节点数；m为配电网总支路数；Ca、Cs、Cd分别为单台 APF、D-STATCOM以及DVR的投资费用。m为设备安装系数，值为1表示相应母线或线路上安装该设备，值为0则表示不安装。h(x)为不等约束约束，考虑了配电网谐波治理目标、功率因数、各负载正常工作电压范围及设备安全运行的容量限制，如式(3)~(7)所示。

式中：THDhi和 THDui分别为配电网公共接入点(PCC节点)的电流和电压总谐波畸变率；为 PCC节点功率因数；CT和CH分别为规定的总谐波畸变率的限值；Ihi和I1i分别为节点i的h次谐波电流分量和基波电流分量；Uhi和U1i分别为i节点h次谐波电压分量和基波电压分量；jC为规定的用户功率因数下限；Ui为节点 i的电压，Uimin和 Uimax分别为各节点电压上下限，敏感负荷在系统电压发生跌落、暂降等故障时候也需满足该约束，其他负荷在稳态时需满足此约束；S为各装置实际输出容量；SN为各装置额定容量列向量；ks为各装置容量过载系数。

2 定制电力设备优化配置智能混合算法

单纯的遗传算法在一些大规模计算问题上，局部搜索能力差，容易陷入“早熟”，在进化后期搜索效率低，往往不能找到问题最优解而是次优解。在本文优化配置问题上，单纯运用遗传算法进行寻优时设备安装位置的多次寻优结果是一致的，但相应设备参数的多次寻优结果有出入，虽然相差不大，但在实际应用中仍会造成比较大的损失。为寻找更精确更优秀的设备参数，本文将遗传算法与非线性内点法结合[13]提出智能混合算法用在定制电力设备的优化配置中。算法流程如图1所示，可概括为以下几个步骤。

(1) 利用遗传算法同时处理优化问题中的连续变量和离散变量，从各装置候选安装位置中找到满足约束的最优安装位置，并得到相应位置处设备参数的近似最优解。

(2) 将遗传算法所得最优安装位置锁定，将最优安装位置处设备参数(有效连续变量)输出作为内点法初值。

(3) 利用内点法对设备参数作进一步优化，一系列迭代后可得各装置最优设备参数。

图1 智能混合算法流程图Fig. 1 Flow chart of intelligent hybrid algorithm

2.1 遗传算法优化过程

遗传算法首先对变量进行编码并产生初始种群，根据适应度值的大小决定个体优劣。通过选择、交叉和变异操作向着适应度值增大的方向不断进化，最终求得最优解[14]。本文遗传算法中几个重要环节如下所述。(1) 采用图2混合编码方式，每条染色体由参数基因和控制基因两部分构成，每部分又包括了APF编码区、D-STATCOM编码区和DVR编码区。控制基因采用二进制编码，“ 1”表示该候选位置安装此类设备，“0”表示不安装。参数基因采用十进制编码，从左到右依次决定了对应位置处APF各次谐波电流补偿度、D-STATCOM输出无功功率和DVR输出补偿电压。

(2) 种群规模设置为70代，交叉概率为0.7，变异概率为0.1。收敛判据为最优个体可行，且目标函数连续30代不变，最大迭代次数为100次。

(3) 约束惩罚

对不等约束的处理，采用在目标函数中引入惩罚项来处理，如式(8)。

式中： ()f x为加入惩罚项后的目标函数；Φ为各约束越限量总和，Φ=0表示该个体可行。

图2 遗传算法编码及基因结构Fig. 2 Coding and genetic structure of genetic algorithm

2.2 原-对偶内点法优化过程

对式(1)所描述的非线性规划问题，先将不等式约束转化为等式约束，并把由此引入的松弛变量设成障碍项引入目标函数，形成增广拉格朗日函数[15-16]。

式中：e为各元素都是1的r维列向量，S=diag(s1, s2,L, sr)；Z=diag(z1, z2,L, zr)。运用牛顿迭代求解，化为矩阵相乘形式可得式(11)。

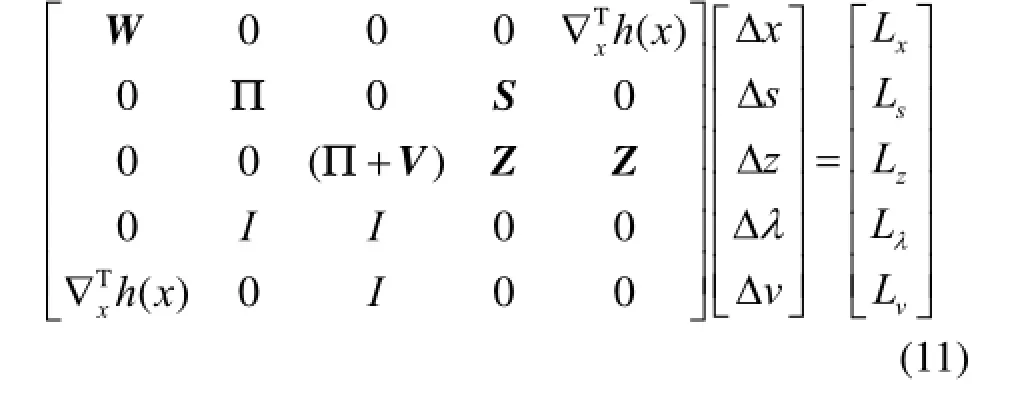
求解式(11)就可以求得原、对偶变量的变化量，选择合适的迭代步长即可不断更新、对偶向量，直到满足收敛条件。若迭代过程不满足收敛判据则按式(13)修改障碍参数。

3 智能混合算法改进

本文针对进智能混合算法进行了以下改进，提高了前半段采用遗传算法的寻优速度，也在一定程度上提高了后半段内点法的寻优速度，保证了所求结果的可行性。

3.1 基于约束越限的初始种群生成方法

大量仿真结果显示，采用随机赋值产生初始种群效率很低，随机产生的个体很难同时满足多个约束。因此本文在随机赋值的基础上，根据约束是否越限加入扩展调整环节，大大加速了初始种群的生成效率。

采用随机赋值方式产生一个个体，如果该个体不满足式(3)~式(5)不等约束，则进行扩展调整。以不满足式(3)为例，式(3)是PCC节点处的电流总谐波畸变率，该值主要取决于染色体APF编码区。因此需要对APF编码区进行扩展调整。判断APF控制基因是否全为“0”，若全为零表示配电网没有APF接入，需重新赋值控制基因直到不全为零；若不全为“0”，则按式(14)进行APF参数基因扩展调整。

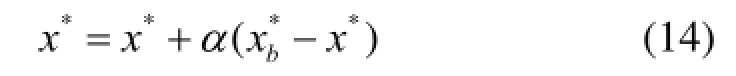
式中：*x表示染色体中APF编码区某一个或多个值为“1”的控制基因所对应的参数基因部分；为 APF参数基因取值上限，即补偿度 100%；a为扩展系数，。

不断重复这个过程就可得到含有一定数量可行个体的初始种群。

3.2 基于预判迭代次数的自适应取值方法

内点法中心参数的取值至关重要，若取值不当会导致收敛速度过于缓慢或造成寻优结果不可行。本文提出一种基于预判迭代次数的自适应s取值方法。首先给s赋较小初值，使r能以较快速度收敛，但这对解的可行性不利。因此，在每次迭代完成时对剩余迭代次数l进行预判断，当l小到一定值后需增大s。仿真过程中发现，r每次迭代近似以相同系数l减小，因此l可表示为

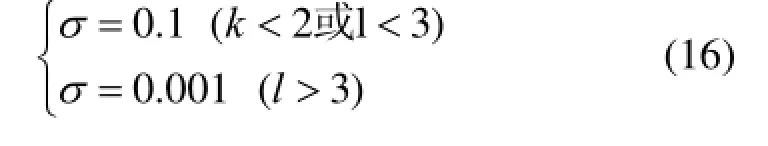
4 仿真算例

以图3所示15节点配电网为例，系统基准电压为12.6 kV，基准容量为10 MVA。节点3、11、14处有谐波负荷，节点6、9、13处有无功负荷，节点5、7、12处有敏感性负荷。配电网PCC节点电流总谐波畸变率为13.49%，总电压畸变率为8.88%，功率因数为 0.779，系统电压发生 30%暂降时，节点5、7、12处线电压有效值分别降至8.53 kV、8.48 kV和8.72 kV。因此需要进行电能质量改善，要求改善后，PCC节点总电流畸变率降到5%以下，总电压畸变率降至3.2%以内，功率因数达到0.9以上。此外，敏感负荷节点电压始终维持在 %5± 以内。

图3 15节点配电网网络拓扑图Fig. 3 Topology structure of distribution network with 15 nodes

根据实际工程经验，选择各装置候选安装位置在谐波源、无功负荷、敏感负荷所在节点以及同类负荷的共同馈出节点。例如图3中，若节点6、15都带有谐波负荷，则候选安装位置为4、6、15。按照这种规则，APF候选安装位置为节点2、3、11、14；D-STATCOM候选安装位置为节点2、3、6、9、13；DVR候选安装位置为线路2、4、6、11。

采用遗传算法求解，可以从图4寻优过程图看出，遗传算法在迭代42次后完成收敛，目标函数降至154.955万元，继续迭代目标函数已经不能继续减小。

采用智能混合改进算法，将遗传算法寻优结果中最优安装位置对应的设备参数输出，化成列向量形式。将其设为内点法初值x(0)，松弛变量和拉格朗日乘子初值分别为。收敛判据为互补间隙，进一步寻优设备参数。从图4可看出，内点法在遗传算法基础上又进行了多次迭代，最终将目标函数减小到150.19万元。

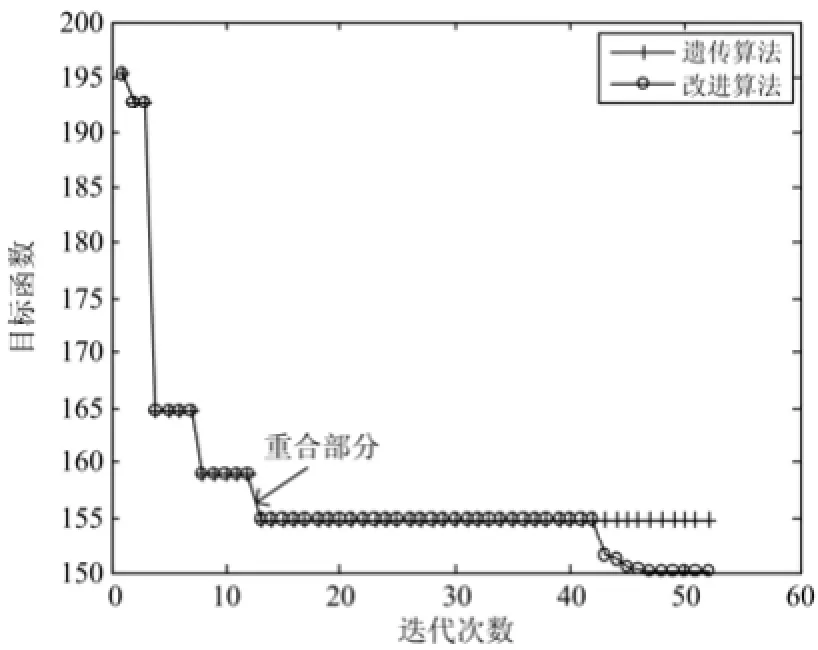
图4 遗传算法与改进寻优过程比较Fig. 4 Comparison of optimization by genetic algorithm and improved algorithm

智能混合改进算法和遗传算法的对应优化结果见表1和表2。由表1可知，智能混合改进算法和遗传算法得到的最优安装位置是一致的，但混合算法求得最优安装容量更小，得到了进一步的优化。由表2可以看出本文采用的智能混合改进算法，在满足电能质量改善要求的前提下，得到了更加满意的投资费用，比遗传算法优化结果小了 3.08%，这在实际应用中会节约很大资本。

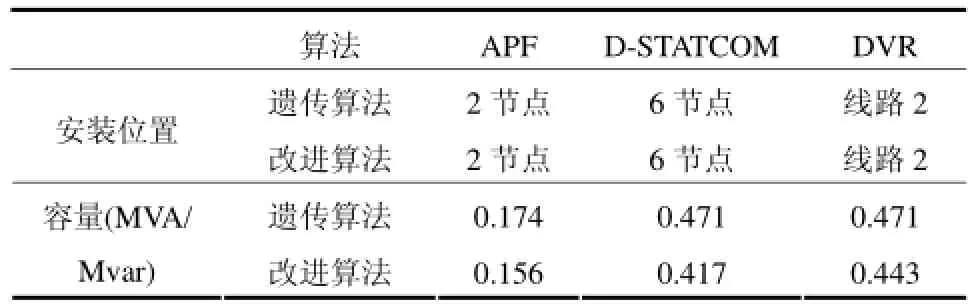
表1 优化结果比较Table 1 Comparison of optimization results

表2 电能质量优化结果Table 2 Simulation results of power quality

另外，本文运用遗传算法进行了大量仿真发现，得到优化结果存在差异，输出目标函数在 152~163万元之间，波动幅度为 7.24%，证明遗传算法寻优稳定性较差，容易陷入局部最优的缺陷。而采用智能混合改进算法后，多次寻优结果都在 150.2±0.2万元以内，波动幅度仅为0.266%，这说明改进算法有很好的稳定性，计算结果比遗传算法更为精确可靠。

5 结论

本文所用智能混合改进算法结合了遗传算法全局搜索能力强、易于处理离散变量以及非线性内点法局部搜索能力强、计算结果精确的优势，解决了遗传算法过早收敛且稳定性较差的缺陷。在定制电力设备的优化配置中运用该算法，在满足电能质量改善目标前提下，将设备投资降至更低。算例仿真验证了改进算法的可行性和优越性，为电能质量改善装置的优化配置问题提供了参考，有一定的实际应用价值。

[1] 田培涛, 黄金海, 吴庆范, 等. 直流滤波器保护关键问题的研究[J]. 电力系统保护与控制, 2015, 43(18): 144-149.

TIAN Peitao, HUANG Jinhai, WU Qingfan, et al. Study on the key problems of DC filter protection[J]. Power System Protection and Control, 2015, 43(18): 144-149.

[2] 文维娟. STATCOM 的控制方法与主电路研究[D]. 镇江: 江苏大学, 2008.

WEN Weijuan. Study on the control method and the main circuit of STATCOM[D]. Zhenjiang: Jiangsu University, 2008.

[3] 周静, 韦统振, 赵艳雷, 等. 低压配电网中单相动态电压恢复器与电力系统之间的能量流动[J]. 电力自动化设备, 2010, 30(4): 26-30.

ZHOU Jing, WEI Tongzhen, ZHAO Yanlei, et al. Energyflow between power system and single-phase DVR in low-voltage distribution system[J]. Electric Power Automation Equipment, 2010, 30(4): 26-30.

[4] ESMAEIL G, INNOCENT K. Optimal placement of multiple-type FACTS Devices to maximize power system loadability using a generic graphical user interface[J]. IEEE Transactions on Power Systems, 2012, 28(2): 764-778.

[5] OMID G, VAHID R, IMAN N. Power system security improvement with optimal placement of FACTS devices using genetic algorithms[C] // 2011 International Conference on Computer Applications and Industrial Electronics.Penang, Malaysia: IEEE, 2011: 126-131.

[6] 盛晓光, 韦统振, 马明, 等. 配电网中多台动态电压恢复器的优化配置研究[J]. 电网技术, 2013, 37(10): 2991-2996.

SHENG Xiaoguang, WEI Tongzhen, MA Ming, et al. Optimal configuration of multiple DVRs in distribution network[J]. Power System Technology, 2013, 37(10): 2991-2996.

[7] 王艳松, 刘军, 李中树. 配电网无源滤波器的优化配置[J]. 高电压技术, 2010, 36(9): 2324-2328.

WANG Yansong, LIU Jun, LI Zhongshu. Optimal configuring of passive filters in distribution network[J]. High Voltage Engineering, 2010, 36(9): 2324-2328.

[8] 上官海洋, 向铁元, 张巍, 等. 基于智能优化算法的FACTS设备多目标优配置[J]. 电网技术, 2014, 38(8): 2193-2199.

SHANGGUAN Haiyang, XIANG Tieyuan, ZHANG Wei, et al. Intelligent optimization algorithm based multiobjective optimal configuration for FACTS equipments[J]. Power System Technology, 2014, 38(8): 2193-2199.

[9] 冯兴田, 孙添添, 马文忠. 配电网电能质量调节装置集散配置策略[J]. 电力系统保护与控制, 2015, 43(24): 33-39.

FENG Xingtian, SUN Tiantian, MA Wenzhong. Centralized and dispersed allocation strategy of power quality regulating devices in distribution network[J]. Power System Protection and Control, 2015, 43(24): 33-39.

[10] 韩璐, 李凤婷, 周二雄, 等. 基于成本-收益的微网分布式能源优化配置[J]. 电工技术学报, 2015, 30(14): 388-396.

HAN Lu, LI Fengting, ZHOU Erxiong, et al. The distributed energy optimization configuration of micro-grid based on cost-benefit[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 388-396.

[11] 陈洁, 杨秀, 朱兰, 等. 基于遗传算法的热电联产型微网经济运行优化[J]. 电力系统保护与控制, 2013, 41(8): 7-15.

CHEN Jie, YANG Xiu, ZHU Lan, et al. Genetic algorithm based economic operation optimization of a combined heat and power microgrid[J]. Power System Protection and Control, 2013, 41(8): 7-15.

[12] 刘振国, 胡亚平, 陈炯聪, 等. 基于双层优化的微电网系统规划设计方法[J]. 电力系统保护与控制, 2015, 43(8): 124-133.

LIU Zhenguo, HU Yaping, CHEN Jiongcong, et al. A planning and design method for microgrid based on two-stage optimization[J]. Power System Protection and Control, 2015, 43(8): 124-133.

[13] 丁晓群, 王艳华, 臧玉龙. 基于内点法和改进遗传算法的无功优化组合策略[J]. 电网技术, 2008, 32(11): 45-49.

DING Xiaoqun, WANG Yanhua, ZANG Yulong. A combination strategy for reactive power optimization based on predictor-corrector interior point method and improved genetic algorithm[J]. Power System Technology, 2008, 32(11): 45-49.

[14] 雷德明, 严新平. 多目标智能优化算法及其应用[M].北京: 科学出版社, 2009: 23-26.

[15] 聂永辉, 杜正春，李崇涛. 考虑风电接入的大型电力系统多目标动态优化调度[J]. 电工技术学报, 2014, 29(10): 286-295.

NIE Yonghui, DU Zhengchun, LI Chongtao. Multiobjective dynamic optimal dispatch for large-scale power systems considering wind power penetration[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 286-295.

[16] YAN Xihui, VICTOR H. Improving an interior-pointbased OPF by dynamic adjustments of step sizes and tolerances[J]. IEEE Transactions on Power Systems, 1999, 14(2): 709-717.

冯兴田(1978-)，男，博士，讲师，主要研究方向为电力系统电能质量分析与控制技术；E-mail: topfxt@163.com

孙添添(1991-)，女，硕士研究生，主要研究方向为电能质量改善装置控制策略研究与分析；

马文忠(1968-)，男，博士，教授，主要研究方向为电力电子技术与电机拖动控制、分析与设计。

(编辑 姜新丽)

Optimal configuration strategy of custom power devices based on intelligent improved algorithm

FENG Xingtian, SUN Tiantian, MA Wenzhong
(College of Information and Control Engineering, China University of Petroleum (East China), Qingdao 266580, China)

In order to solve power quality problems more effectively such as harmonic pollution, low power factor as well as the sensitive loads not to work properly because of voltage sags, flickers and so on. The optimal configuration of custom power devices is studied. By considering power quality improving goals and total investment cost, a mathematical model is proposed for optimization. Besides, a mixed optimization algorithm that combines genetic algorithm and interior-point method is proposed for the optimal configuration of multi-type custom power devices. This mixed strategy uses genetic algorithm to find the optimal location and approximate optimal capacity of each device. Then the approximate capacity will be set as the initial value of the interior-point method, and more accurate capacity can be calculated through interior-point method. Besides, some improvements are made in the process of genetic algorithm and interior-point method. These improvements can speed up the convergence. Theoretical analysis and simulation results indicate that this mixed algorithm has better stability, and more accurate results can be obtained than through traditional genetic algorithm. This work is supported by National Natural Science Foundation of China (No. 51477184 and No. 61271001) and Fundamental Research Funds for the Central Universities (No. 14CX02085A).

genetic algorithm; interior-point method; optimal configuration; power quality; custom power devices

2015-10-27；

2016-01-01作者简介：

10.7667/PSPC151893

国家自然科学基金项目(51477184，61271001)；中央高校基本科研业务费专项资金项目(14CX02085A)