基于Karhunen-Loeve变换的GPS弱射频干扰检测
2016-04-12陈鹏飞孙克文
陈鹏飞, 孙克文
(合肥工业大学 计算机与信息学院,安徽 合肥 230009)
基于Karhunen-Loeve变换的GPS弱射频干扰检测
陈鹏飞,孙克文
(合肥工业大学 计算机与信息学院,安徽 合肥230009)
摘要:干扰是无线电通信系统最大的威胁之一,干扰检测对于全球导航卫星系统(Global Navigation Satellite System,GNSS)信号非常重要。为了检测GPS(Global Positioning System)信号中射频干扰,文章提出了一种新型的基于Karhunen-Loeve变换(KLT)射频干扰(RFI)的检测算法。通过GPS信号模拟器生成GPS L1信号,并在射频前端叠加射频干扰;再利用KLT对其数字中频信号进行分析和处理,得到相关矩阵(Toeplitz矩阵)的特征值,通过特征值重建干扰信号。经过仿真验证,该算法能够成功地检测出干扰信号,包括微弱的干扰信号。
关键词:干扰检测;全球导航卫星系统;Karhunen-Loeve变换;特征值
0引言
近年来,GPS(Global Positioning System)卫星导航被广泛应用于军事、商业和民用等各个领域,起着不可或缺的作用[1-3]。随着新的全球导航卫星系统(Global Navigation Satellite System,GNSS)的出现,如欧盟的伽利略(Galileo)系统、中国的北斗(BD)系统、美国的现代化GPS系统以及俄罗斯格洛纳斯(Glonass)系统,将有越来越多的无线电卫星导航信号发射出去[4]。这些信号在传播过程中容易受到各种干扰,包括射频干扰(RFI)、电离层干扰、多径效应等,其中对射频干扰最为敏感。干扰的存在直接影响卫星导航信号的准确性,导致GNSS接收机定位不准确,严重影响卫星导航系统在日常生活中的应用。
目前,射频干扰的检测与抑制是一个非常热门的研究方向,已经有许多众所周知的方法与算法。对于GNSS软件接收机的干扰检测,常用的分析信号算法有快速傅里叶变换(FFT)和短时傅里叶变换(STFT),它们都可以进行干扰检测且使用方便[5-6];但基于傅里叶变换(FT)的方法主要以傅里叶级数(FS)为基础,必须采用一组确定的正交三角函数系来对信号进行分解,因此有一定的局限性,降低了干扰检测成功的可能性。并且FFT、STFT和FT这3种方法几乎都不能检测微弱的射频干扰信号。
本文运用了一种新的分析信号的数学工具——Karhunen-Loeve变换(KLT),它类似于FT,但不受FT的条件限制[7-8],能够很好地检测出射频干扰信号,即使是非常微弱的射频干扰信号[8]。在利用Matlab软件进行KLT算法仿真过程中,首先利用GPS信号模拟器产生出GPS L1频段的信号,并在射频端叠加线性调频干扰。然后利用KLT对数字中频的GPS信号进行正交展开,其展开系数是随机变量,展开基函数是相关矩阵(或者协方差矩阵)的特征向量(特征函数);其中相关矩阵的特征值λn与特征函数Φn(t)相对应,代表相关特征函数的投影值,而且对于KLT的干扰检测和滤波性能具有重大意义。最后通过对特征值数目和大小的分析,划分出干扰子空间信号空间,以实现干扰信号的检测。
1KLT描述
KLT可以把(0,T)时间内的观测信号利用一组标准正交函数系展开成一个特殊的级数,这组正交函数系由待分析的信号确定,展开系数为随机变量。但是KLT也存在一定的缺陷,即在实际运算过程中计算量很大。而随着计算机硬件技术的快速发展以及研究人员的努力,KLT正在得到广泛使用。
KLT是一个信号的正交变换,应用KLT处理一个随机过程X(t),它的基本离散展开式为:
(1)
X(t)的KLT展开式与傅里叶级数类似,其中,X(t)为待分析的或待分解的信号;Zn为随机变量,相当于傅里叶级数的系数;Φn(t)为信号的特征向量或特征函数,相当于傅里叶级数的三角函数。在向量空间中使用特征函数是一个常用的分解过程,而且在理论上有很多的分解形式。必须要指出的是,傅里叶级数中的三角函数系和KLT展开式中特征函数都必须正交。然而,KLT的特征函数Φn(t)的类型一般是未知的,要根据被处理的信号确定,这与傅里叶级数必须是正弦和余弦函数不同。在KLT方法中,待处理信号通常是一个有限区域,因此KLT不仅适用于周期信号,也适用于非周期信号。同时随机过程X(t)的展开系数Zn是随机变量,反映待分析数据的随机特性,即
(2)
KLT展开式的系数Zn的方差即为特征值,用变量λn描述。特征值λn与特征函数Φn(t)一一对应,代表相关特征函数的能量值,同时特征函数和信号的自相关函数E{XkXl}有如下关系:
(3)
其中,E{XkXl}为一个N×N阶的托布利兹(Toeplitz)自相关矩阵。(3)式可以采用矩阵特征值求解方法进行特征值与特征向量的求解,特征值表示相应的特征向量的能量,并且对于KLT干扰检测非常重要[9-10]。
2KLT干扰检测分析
2.1KLT实现射频干扰检测整体流程
KLT分析的数据是经过采样和量化的数字中频信号,其中信号由GPS信号、高斯白噪声和线性调频干扰3部分组成,KLT的检测对象是射频干扰即高动态干扰信号,所以选用线性调频干扰[11]。在对随机信号进行KLT分解时,实现无限分解是不可能的,也是不必要的,因为KLT是可用于消除干扰、具有最小均方误差的一种最优变换,所以可以选择前N项进行分析。KLT实现GPS信号中线性调频干扰检测的整体流程如图1所示。
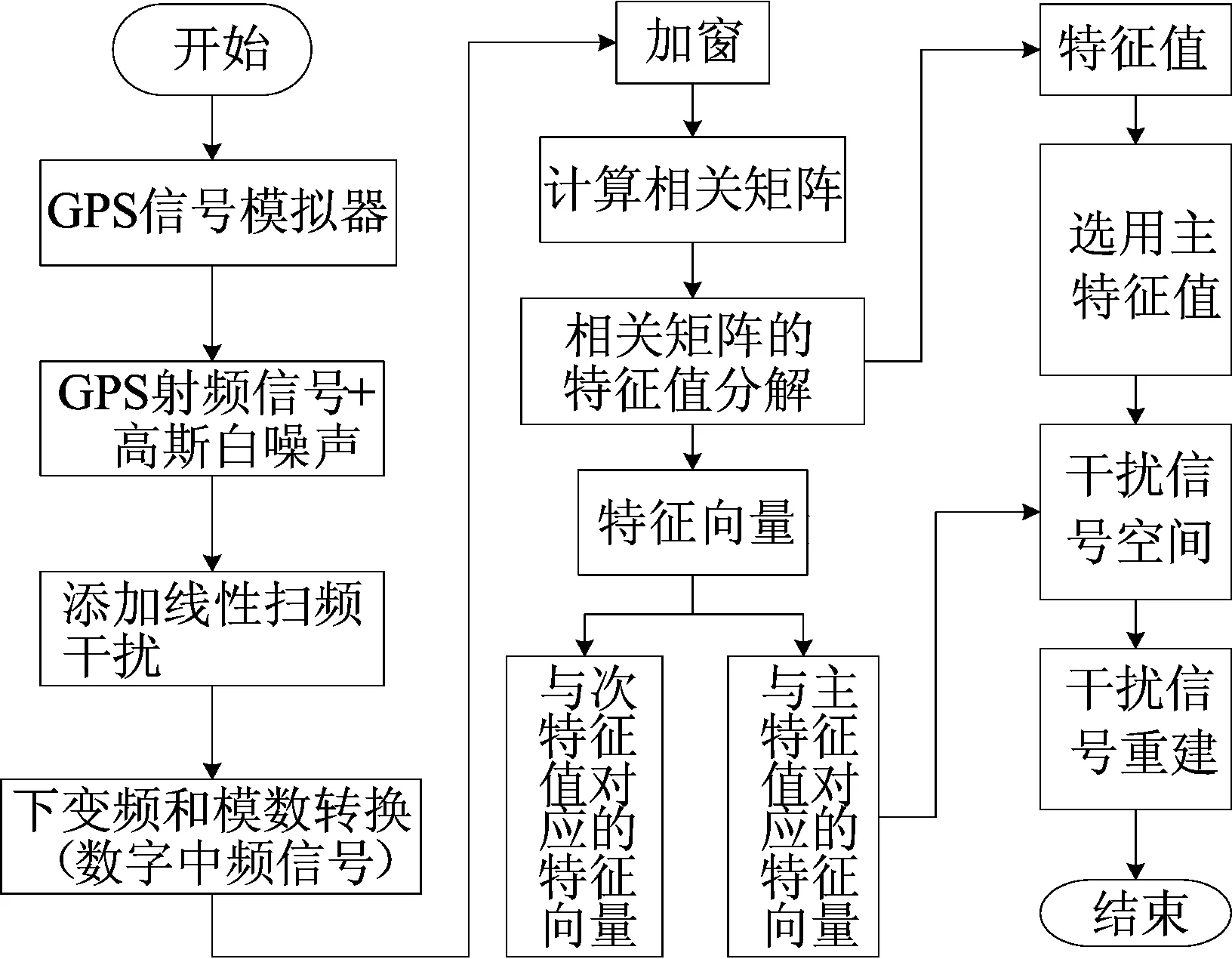
图1 KLT实现射频干扰检测整体流程
KLT实现干扰检测的基本思想是对待分析数据序列求解相关矩阵(Toeplitz矩阵)。首先对相关矩阵进行特征值分解,求出特征值和特征向量;然后对特征值进行分析和处理,求出主特征值(较大的特征值)与次特征值(较小的特征值),主特征值对应射频干扰的随机特性;最后依据相应特征值对应的特征向量,实现对射频干扰的检测和干扰信号重建。
2.2特征值与特征向量分析
在数学意义上,把矩阵所表示的空间进行正交分解,特征向量就是矩阵在每一维空间上的基函数。在信号处理过程中,特征值代表相应特征向量的能量。在离散时间的KLT中最重要的是特征值和特征向量。特征值序列总是收敛的,无论分析的数据是什么,只要求解相关矩阵或者协方差矩阵的特征值序列,那么特征值序列一定收敛。例如,对于一个最简单的正弦信号,其特征值序列最终趋于0,前面几个主特征值代表了信号的主要能量。正弦函数的相关矩阵特征值序列如图2所示,其中前面4个明显较大的特征值即主特征值,代表信号的主要能量。根据特征值的特性,选用主特征值及其对应的特征向量即可进行干扰信号重建。

图2 正弦函数的相关矩阵特征值序列
同样地,GPS信号和线性调频干扰的相关矩阵或者协方差矩阵的特征值序列也是收敛的,最终趋于0。只是在进行GPS信号的干扰检测中,分析数据量太大,依据特征值序列总是收敛的特性,只需要对前面的M个特征值进行分析,因此没必要显示所有的特征值。
2.3特征值序列与干扰子空间和信号子空间
特征值是信号子空间和噪声子空间各维能量的一种反映,根据特征值分布的差异情况,结合信号与干扰和噪声可能存在的特性,利用特征值区分信号子空间和噪声子空间。在基于MUSIC算法的信号子空间与噪声子空间中,将相关矩阵的特征值从大到小排列,则信号子空间对应的是主特征值即前面几个明显较大的特征值,而噪声子空间对应的是次特征值即剩下的较小特征值。由于GPS信号的特性与高斯白噪声的非常类似,而且检测的目标是高动态干扰信号——线性调频信号,因此在特征值序列中主特征值对应的是线性调频干扰即射频干扰,而次特征值序列对应GPS信号空间。
对于射频信号,前几个比较大且变化较大的特征值反应了目标信号即线性调频干扰信号,而其余较小且较为平缓的特征值反应的是GPS信号本身。信噪比C/No=50、干噪比JNR=0.1的GPS信号特征值序列的分布(只显示了部分的特征值)如图3所示。由图3可以看出,前3个特征值明显大于后面的特征值,而且差距很大,因此,可以认为前3个特征值对应着线性调频干扰的干扰子空间。

图3 GPS信号的相关矩阵特征值序列
3实验仿真
下面研究分析KLT信号处理算法的性能,通过Matlab软件仿真验证基于KLT的GPS射频干扰检测。试验中所用射频干扰信号为chrip信号,又称为线性调频信号(linear frequency modulation,LFM),所以主要的干扰检测对象是线性调频干扰,LFM干扰信号模型为:
(4)
其中,A为信号幅度;f=f1+Kt,f1为线性调频的起始频率,K=B/T为调频斜率,B为调制带宽,T为扫频时间。
首先需要将线性调频干扰按照要求添加到GPS卫星射频信号中,近似模拟实际环境中GPS信号受射频干扰影响的情景;然后对天线接收的信号进行下变频和模数转换,变成数字中频信号;最后对此数字中频信号利用KLT算法进行干扰检测和干扰滤除。
常见的GPS信号模拟器产生的都是数字中频信号[12-14],方便后续硬件处理或者计算机仿真算法研究的实现。GPS信号模拟器产生的没有噪声与干扰的GPS信号时域图、频谱图和功率谱密度图如图4所示。

图4 无噪声与干扰GPS信号模拟器产生的GPS信号
GPS信号通常混有高斯白噪声,因此选用信噪比C/No=50的GPS信号。在进行线性调频干扰叠加时,需要考虑信号与干扰的相对强弱来衡量信号质量,同时也可以用来分析KLT检测算法的性能。信号与干扰的衡量指标通常有干信比(jamming-to-signal ratio,JSR)和干噪比(jamming-to-noise ratio,JNR)。JSR是目标接收机处的干扰功率与信号功率之比,其意义同信噪比(signal-to-noise ratio,SNR)类似,表示信号的质量状况,其定义如下:

(5)
其中,PJ为干扰信号功率;PS为信号功率。与SNR不同,JSR越小越好,JSR越小表明信号的功率越强、质量越好。JNR是借助于SNR来表示干扰与信号的相对强弱的,其定义如下:
(6)
在添加干扰时对JNR进行设置,根据C/No和SNR求出噪声功率,利用(6)式求出干扰信号的功率及幅值,确定要加入的线性调频干扰信号。当C/No和SNR固定时,JNR越大即线性调频干扰越强;JNR越小,线性调频干扰越弱。本实验中JNR=0.3表示强干扰,JNR=0.01表示弱干扰。
选用C/No=50的信号,分别设定JNR=0.3和JNR=0.01,用FFT对其进行谱估计,得到功率谱密度图如图5所示。由图5a可以看出,在强干扰下FFT可以容易地检测出射频干扰;由图5b可以看出,在弱干扰下FFT几乎检测不到干扰,只能看到一些噪声存在。

图5 强、弱干扰下FFT谱估计
采用KLT对弱干扰信号进行检测,设定JNR=0.01,C/No=50,按照图1所示的KLT实现射频干扰检测整体流程,对待分析数据序列求解相关矩阵(Toeplitz矩阵),然后对特征值进行分析和处理,求出主特征值与次特征值,得到的相关矩阵特征值序列如图6所示。主特征值对应射频干扰的随机特性,依据相应特征值对应的特征向量,实现对射频干扰的检测和干扰信号重建。

图6 JNR=0.01,C/No=50相关矩阵特征值序列
图6中,前2个特征值为主特征值,利用主特征值和其对应的特征向量进行干扰信号重建。在时频平面上可以清楚、直观地观察到重建后的扫频干扰信号,重建的弱扫频干扰信号的三维图如图7所示。

图7 重建的弱扫频干扰信号的三维图
通过以上实验可知,在弱扫频干扰的情况下KLT可以检测出GPS信号中的扫频干扰,而基于FFT的谱估计则未检测出来。
4结束语
本文提出了一种新型的基于Karhunen-Loeve变换(KLT)的射频干扰(RFI)检测算法,它所用的基函数可以是任何形式,能够对信号实现更好的分解,是一种更灵活的变换;通过对比可知,KLT能够有效地检测出GPS接收机中的微弱干扰信号,具有FFT不具备的优点。虽然KLT处理信号需要很大的计算量,但是随着计算机技术的发展,KLT这种高性能的数学工具,在未来的信号分析和处理中将会发挥越来越大的作用。
[参考文献]
[1]谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2012:1-40.
[2]Kaplan E D,Hegarty C J.Understanding GPS principles and applications[M].Artech House,2005:1-19.
[3]谢钢.全球导航卫星系统原理:GPS、格洛纳斯和伽利略系统[M].北京:电子工业出版社,2013:116-161.
[4]Sun K,Liu W,Xu H,et al.Interference detection based on time-frequency analysis for GNSS receivers[C]//Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation.Institute of Navigation,2013:3577-3585.
[5]Sun C,Jan S.GNSS interference detection and excision using time-frequency representation[J].Proceedings of the International Technical Meeting of the Institute of Navigation,2011,8034(6):365-373.
[6]刘伟,孙克文,陶帅.基于时频分析的GNSS连续波干扰检测[J].合肥工业大学学报:自然科学版,2014,37(9):1089-1092.
[7]Maccone C.Mathematical SETI:statistics,signal processing,space missions[M].Berlin:Springer,2012:411-448.
[8]Maccone C.Deep space flight and communications:exploiting the sun as a gravitational lens[M].Berlin:Springer,2009:91-95.
[9]Szumski A,Eissfeller B.The Karhunen-Loève transform as a future instrument to interference mitigation[C]//Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation.Institute of Navigation,2013:3443-3449.
[10]Ai X H,Li W B V.Karhunen-Loeve expansions for them-th order detrended Brownian motion[J].Science China:Mathematics,2014,57(10):2043-2052.
[11]刘前刚,刘宏立.GPS接收机抗射频干扰技术研究[J].计算机测量与控制,2009,17(7):1353-1355.
[12]李成军,陆明泉,冯振明.GPS中频信号模拟器的数学模型及实现[J].清华大学学报:自然科学版,2008,48(10):1582-1585.
[13]王金刚.GPS数字中频信号仿真及捕获验证[J].重庆邮电大学学报:自然科学版,2010,22(2):252-256.
[14]赵钧,张其善,寇艳红.基于Matlab的数字中频GPS信号生成模型[J].信号处理,2005,21(3):300-303.
(责任编辑胡亚敏)
Weak radio frequency interference detection of GPS based on Karhunen-Loeve Transform
CHEN Peng-fei,SUN Ke-wen
(School of Computer and Information, Hefei University of Technology, Hefei 230009, China)
Abstract:Interference is one of the biggest threats to radio-communication system. Therefore, interference detection is greatly important for Global Navigation Satellite System(GNSS). In order to detect radio frequency interference(RFI) in Global Positioning System(GPS) signal, a novel RFI algorithm based on Karhunen-Loeve Transform(KLT) is proposed in this paper. GPS L1 signal is generated through GPS signal simulator and RFI is added to RF front-end. Then, by using KLT analysis and processing of their digital IF signal,the correlation matrix(Toeplitz matrix) eigenvalues are obtained, which can reconstruct interference signals. The simulation results show that the proposed algorithm can successfully detect the interference signal, even a weak signal.
Key words:interference detection; Global Navigation Satellite System(GNSS); Karhunen-Loeve Transform(KLT); eigenvalue
中图分类号:TN967.1
文献标识码:A
文章编号:1003-5060(2016)02-0194-05
Doi:10.3969/j.issn.1003-5060.2016.02.010
作者简介:陈鹏飞(1989-),男,安徽庐江人,合肥工业大学硕士生;孙克文(1979-),男,安徽马鞍山人,博士,合肥工业大学教授,硕士生导师.
收稿日期:2014-12-30;修回日期:2015-03-02
