大直径桩在三维黏弹性土体中瞬态振动数值计算

张　健,　刘东甲,　卢志堂,　姜　静,　耿　笑,　高子杰

(1.合肥工业大学 资源与环境工程学院,安徽 合肥　230009; 2.同济大学 地下建筑与工程系,上海　200092)



大直径桩在三维黏弹性土体中瞬态振动数值计算

张健1,刘东甲1,卢志堂2,姜静1,耿笑1,高子杰1

(1.合肥工业大学 资源与环境工程学院,安徽 合肥230009; 2.同济大学 地下建筑与工程系,上海200092)

摘要:为了更加深入地进行桩基低应变数值模拟计算,文章将桩土均视为黏弹性体,建立了三维条件下桩-土系统瞬态振动计算模型;利用交错网格有限差分法求解三维黏弹性波动方程,引入吸收边界,得到了完整桩在瞬态竖向激振力作用下的动力响应;通过对比不同黏弹性参数作用时三维(3D)条件下桩顶振动速度响应,对桩土黏弹性参数进行了分析;对桩顶不同拾振位置曲线进行模拟,求得了黏弹性条件下大直径桩的最佳拾振位置,直观地反映了波在桩中的传播特点,对工程实践具有一定的指导意义。

关键词:黏弹性体;有限差分法;三维桩土模型;吸收边界;最佳拾振位置

桩基础广泛应用于工程实践中,是一种十分重要的基础形式,对桩基础质量的快速检验是十分必要的。随着大直径桩越来越广泛地使用,传统的一维杆模型已经不能完全真实地反映实际三维情况,并且实际存在的缺陷比较复杂,又由于三维效应的干扰,使得曲线分析难度加大,因此对三维桩基振动的数值模拟计算研究十分必要。对于桩-土系统的瞬态激振问题,文献[1]利用有限差分法对完整桩进行了瞬态纵向振动的数值模拟计算,取得了良好的应用效果;文献[2]在三维条件下,通过差分法对三维直角坐标系下大直径桩完全弹性模型进行了模拟计算,直观地反映了波在桩中传播特点;文献[3]在三维条件下,通过变步长交错网格有限差分法对三维桩基弹性波动方程进行了数值计算,在保证计算精度的前提下提高了计算效率;文献[4]通过对承台-桩系统进行三维数值计算,对比分析了不同吸收边界下桩-土系统的振动特点;文献[5]对在考虑土体三维波动效应时黏性阻尼土中桩的耦合作用进行了研究,揭示了桩纵向振动特性;文献[6]分析桩-土相互作用的黏弹性土中管桩的纵向动力阻抗,讨论了桩周土和桩芯土剪切模量比、黏滞阻尼系数比和管桩内外半径比对管桩竖向动力阻抗的影响;文献[7]通过理论试验研究,提出了简单确定Kelvin模型黏弹性材料参数的实验方法;文献[8]对三维非均质土中黏弹性桩-土纵向耦合振动响应进行了研究,通过分析桩土参数对桩顶动力响应的影响,得到了桩顶频域和时域响应的规律。已有研究将黏弹性桩当做一维杆,对桩-土系统进行模拟,但是当桩径较大时,一维杆并不能完全反应实际情况。

在已有的三维桩研究中,为了研究和求解的简便,常常将桩、土都视为完全弹性体,但由于天然土层一般成层分布,土粒之间的孔隙中存在着空气和水,具有黏滞性质,因此为了更加符合实际,本文将桩、土均视为黏弹性介质,建立三维黏弹性桩土模型来研究大直径桩的振动响应。

1三维桩土模型及定解问题

建立桩土模型。假定桩、土为各向同性的线性黏弹性介质,λ1和μ1为弹性部分的胀缩和剪切特性;λ2和μ2为黏性部分的胀缩和剪切特性,黏弹性本构模型采用Kelvin-W. Voigt模型,结构模型由弹性模型和黏滞模型并联而成,如图1所示。

图1　黏弹性本构模型

动力本构表达式为:

(1)

其中,σd1为弹性部分的应力;σd2为黏性部分的应力;εd为应变;弹性和黏性应变相等,E和C分别为弹性模量、黏滞系数。

已知桩长为L，桩径为D，桩身密度、拉梅常数和黏滞系数分别为ρp、λp、μp、Cp,对桩顶施加一个作用半径为r0的纵向激振力P(t)。桩周土的密度、拉梅常数和黏滞系数分别为ρs、λs、μs、Cs；桩底土的密度、拉梅常数和黏滞系数分别为ρb、λb、μb、Cb。三维桩土模型示意图如图2所示。

图2　三维桩土模型示意图

低应变测试时,假设桩土不分离,同时不考虑体力,将桩身、桩周土和桩底土看作各向同性的线性黏弹性体。桩-土系统振动的黏弹性波动方程可以表示为:

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

其中,vx、vy、vz分别为质点振动的速度分量;σx、σy、σz、τxy、τxz、τyz分别为正应力分量和剪应力分量;ρ为密度;λ1、μ1和λ2、μ2分别为弹性部分和黏性部分的拉梅常数。

纵向激振力P(t)的表达式为:

(11)

其中,I、t0分别为激振力冲量和作用时间。

对于初始条件的设置,由于桩顶在未受激振力作用时,三维桩-土系统处于完全静止,故整个桩-土系统中质点的速度分量与应力分量均为0。

对于边界条件的设置,在桩顶位置处,纵向激振力所取参数为:

(12)

在波动方程的数值计算过程中,由于计算机内存和计算时长的限制,需要对桩-土系统的计算区域进行截取,保证数值计算能在有限的区域范围内得到实现。本文采用Higdon吸收边界条件[9],对桩土模型边界处的速度和应力分量进行吸收处理,以x方向边界为例,吸收边界条件表示为:

(13)

(13)式的差分算子可以用有限差分近似表示为:

(14)

其中,αj为吸收入射角;c为传播速度;m为吸收边界条件的阶数。本文采用二阶吸收边界和盒式差分法,因此m=2,a=0.5,b=0.5。

2定解问题的差分离散

采用交错网格[10]进行差分离散,把速度分量和应力分量分别定义在2套不同的网格上,这样不仅保证了计算精确度,又保证了速度和应力的连续性。利用交错网格有限差分公式对(2)～(10)式进行差分离散,假定差分算子为：

得到的差分方程如下:

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

对于桩周土六面体边界,采用吸收边界进行处理。在桩-土柱面边界处,波动方程中黏弹性体的密度和拉梅系数都是变化的量,需进行如下的离散取值,即

(24)

(25)

(26)

其中,ρl、ρr、ρt、ρbo、ρf、ρba的下标分别表示采样点相邻的左、右、上、下、前、后的单元。

同理,对于方程(18)～(23)式中μ1、μ2的取值按如下格式得出:

(27)

(28)

(29)

通过这样处理,对不均匀介质的波动方程,只需调整对应界面处的材料参数值,即可保证速度和应力连续,且差分格式保持不变。

3工程实例与数值计算对比

对合肥工业大学某模型桩场地1#完整桩进行数值模拟,1#桩是混凝土灌注桩。根据勘察报告,相关数据为:桩身密度ρ=2 600 kg/m3,桩长L=7.0 m,桩直径D=0.8 m,泊松比υ=0.28,弹性模量E=35 GPa,土的黏滞系数Cs=40 kPa·s,桩的黏滞系数为Cp=65 kPa·s,激振力冲量I=1 N·s，时间t0=1 ms,土参数见表1所列。

表1　三维模型中的土参数

三维桩土模型尺寸为1.8m×1.8m×8.0m,其中桩周土厚度为0.5m,桩底土厚度为1.0m,网格尺寸为Δx=Δy=0.02m,Δz=0.04m。分别利用三维黏弹性模型和完全弹性模型对1#桩进行数值模拟,得到相应的数值模拟响应,如图3所示。

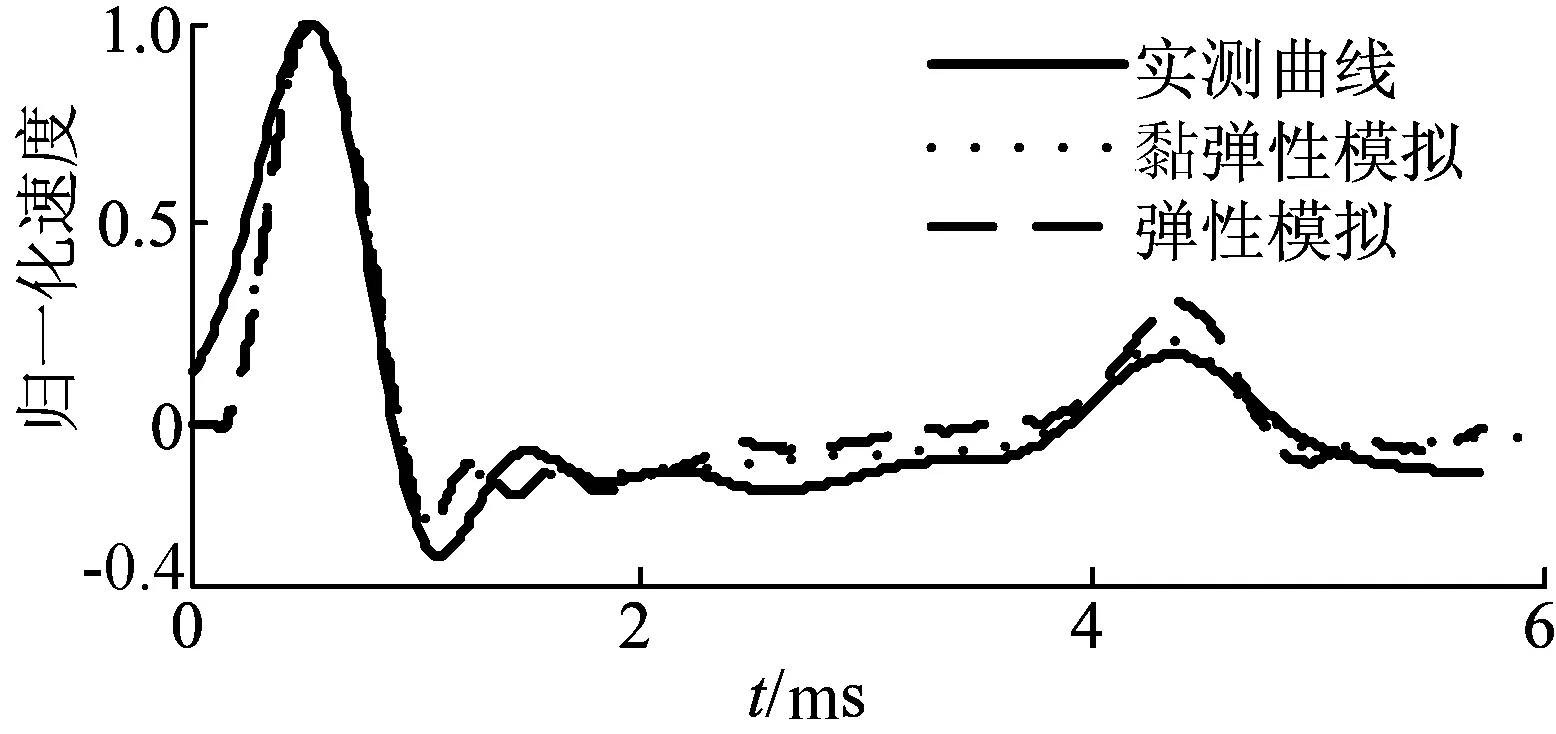
图3　理论曲线与实测曲线对比

由图3可知,数值模拟曲线和实测曲线形态基本吻合,入射波和桩底反射波到时和峰值也比较吻合。由于黏弹性模型把桩土视为三维黏弹性体,与实际更加符合,因此拟合精度比完全弹性模型要好,同时也说明了黏弹性模型交错网格差分计算方法具有良好的计算效果,可以较准确地反映实际情况。

4数值模拟

建立三维桩土模型,桩长L=4.0 m,桩直径D=0.8 m,其他桩土参数同上述模型桩,采用中心激振、0.55R处拾振[11]的方式,模拟桩土在不同黏弹性参数作用下的桩顶振动响应。

4.1桩存在不同黏性时数值模拟

设土黏滞系数Cs=0,桩的黏滞系数分别取Cp1=7 kPa·s,Cp2=70 kPa·s,Cp3=150 kPa·s,模拟得到的理论曲线如图4所示。

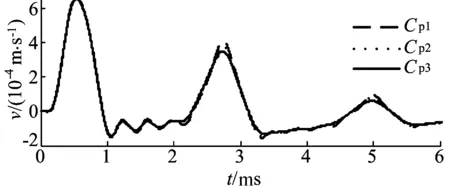
图4　桩存在黏性时的速度对比图

从图4可以看出,随着桩身黏性增大,桩底第1次反射波和第2次反射波振幅峰值出现略微下降,但是反射波到达时间基本一致,并且入射波与反射波之间的干扰震荡变得稍微平缓,说明只有当桩存在黏性时,对波的传播能量造成微小的衰减,并不改变桩顶的振动特性。

4.2土存在不同黏性时数值模拟

设桩黏滞系数Cp=0,土的黏滞系数分别取Cs1=5 kPa·s,Cs2=50 kPa·s,Cs3=100 kPa·s,模拟得到的理论曲线如图5所示。

图5　土存在黏性时的速度对比图

从图5可以看出,随着土的黏性增大,桩周土的黏滞效应对桩的振动作用加强,导致桩底第1次反射波和第2次反射波峰值有所下降。从桩底的第1次反射波可以看出,波的到达时间还基本一致,但是波的振动幅度变宽,到第2次桩底反射波时,波的到达时间出现滞后,幅度变得更宽。

4.3桩、土均有不同黏性时数值模拟

当桩、土都当做黏弹性体,桩、土黏滞系数分别取Cp1=7 kPa·s,Cs1=5 kPa·s;Cp2=50 kPa·s,Cs2=70 kPa·s;Cp3=150 kPa·s,Cs3=200 kPa·s，模拟得到的理论曲线如图6所示。

图6　桩、土都存在黏性时的速度对比

由图6可以看出,在桩、土都具有黏性的情况下,桩底反射波特性有了明显变化,主要是随着桩、土黏性的增大,在桩底第1次反射波就出现了波峰值降低,峰值点到达时间有所延后,并且桩底反射波振动幅度变宽；由于波在桩底传播时程变长,导致第2次反射波变化更为明显；当黏性变得较大时,桩底反射波曲线变得平缓,微小震荡变弱,振动幅度变得很宽。

由以上数值模拟可以得出,桩周土的黏性是造成反射波幅度变宽、振幅变小的主要原因,桩身黏性增大会增强这种影响,但是没有桩周土影响明显。对桩顶拾振点的横向剖面AB进行时间上的连续采样,如图7所示,得到的速度波场图如图8所示。

图7　桩顶拾振点横向剖面示意图

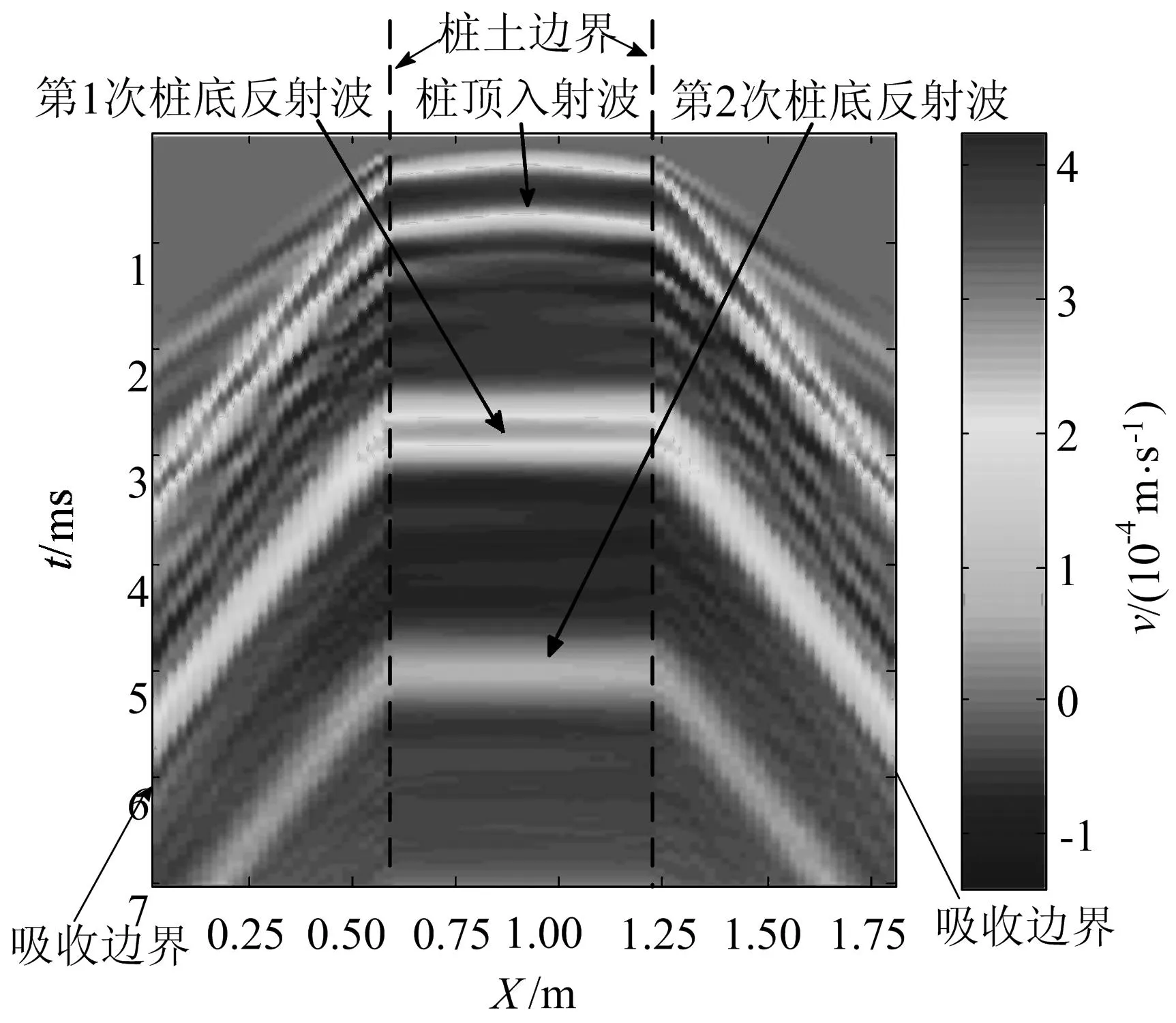
图8　桩顶0.55R处拾振时横向剖面的速度波场图

图8中心处为桩,两边为桩周土。当在中心处激振时,桩顶中点产生较大峰值,随后激振力能量逐渐向周边扩散,达到拾振剖面时传感器接收到较大能量的入射波,随后继续向外传播,当能量到达桩土边界时,会产生一定的反射与透射。最后传到最外层吸收边界处,能量大部分没有发生反射而直接被吸收,从而确保了在较小的桩周土模型下取得比较精确的解,节省了计算机计算时间和计算机内存。当桩底反射波重新回到桩顶时,速度波场图的能量又会增强,从图8中可以清晰地看到在t=2.8 ms左右和t=5.1 ms左右出现了桩底的第1次和第2次反射波,这与实际情况相符,说明了黏弹性模型采用吸收边界具有良好的计算效果。

5中心击振桩顶最佳拾振位置研究

把大直径桩当做三维体来研究,会出现一维杆没有的三维现象,最典型的就是三维效应,即在中心点进行低应变激振时,会在不同拾振点得到不同的桩顶速度响应曲线。本文对三维黏弹性模型下桩-土系统进行研究,找寻最佳拾振位置。

建立三维桩土模型,桩长L=7.0 m,桩直径D=0.8 m,桩土参数取值与第3节相同,桩土黏滞系数分别取Cp1=60 kPa·s,Cs1=50 kPa·s。拾振点分别取在距桩顶中心0.2R、0.5R、0.9R处,模拟得到的理论曲线如图9所示。

图9　桩顶不同拾振位置的速度对比

对图9所示的时域曲线进行傅里叶变换,得到的振幅谱对比图如图10所示。

图10　桩顶不同拾振位置的振幅谱对比图

从图9中可以看出，在中心点激振时,速度响应所受到的三维干扰,先变小后变大。当拾振点在距桩顶中心0.2R处的时候,所受到的三维干扰较大,这主要由于拾振点距离激振点很近,在中点激振时,桩顶中心产生较大峰值,随着激振力消失,桩顶迅速回弹,因此会在拾振处即时产生较大的负向反射,随着拾振位置距桩顶距离变大到0.5R时,三维干扰明显减弱。当距离继续增大到0.9R时,由于靠近桩周土,来自土的扰动变大,三维干扰又有所增强。从图10的振幅谱曲线也可以看出,在0.2R位置处曲线所受到的干扰较大,随着拾振位置变大至0.5R时,干扰变小。

再分别对距桩顶中心0.4R、0.5R、0.7R处拾振,将图形放大,得到的理论曲线如图11所示。

图11　桩顶0.5R处附近速度对比图

从图11可以看出,在0.5R处三维干扰最小,波的振荡也最平缓,说明在此位置拾振会最大限度地排除干扰,提高信噪比。这与文献[11]提出的在三维轴对称模型下拾振位置在0.55R处所受到的三维干扰最小基本一致,说明了桩土的黏弹性对桩顶最佳拾振位置的选取影响不大。

6结论

(1) 本文通过建立三维黏弹性桩土模型,利用交错网格有限差分法计算了三维直角坐标系下桩-土系统的振动问题,得到了瞬态纵向激振力作用下的桩顶低应变数值模拟响应,通过与实测曲线对比,证明了三维黏弹性桩土模型与实际较吻合,取得了良好的应用效果。

(2) 三维黏弹性桩土模型可以有效反映桩土在不同黏弹性参数下的桩顶速度振动响应。随着桩土黏性的增大,桩底反射到达时间会出现滞后,反射点峰值降低,反射波幅度变宽。

(3) 对三维大直径桩最佳拾振位置进行了研究,证明了弹性条件下桩顶最佳拾振位置在0.5R左右处所受到的三维干扰较小,波形较平缓。

(4) 引入吸收边界,对三维黏弹性模型边界处的反射波进行吸收处理,使计算模型的尺寸减小，同时又保证计算机运算的精度。

[参考文献]

[1]刘东甲.完整桩瞬态纵向振动的模拟计算[J].合肥工业大学学报:自然科学版,2000,23(5):683-687.

[2]卢志堂,刘东甲,龙丽丽,等.基桩低应变检测三维问题的数值计算[J].合肥工业大学学报:自然科学版,2011,34(6):905-909.

[3]刘华瑄,刘东甲,卢志堂,等.桩基三维弹性波动方程变步长交错网格有限差分数值计算[J].岩土工程学报,2014,36(9):1754-1760.

[4]Jiang J,Liu D J,Lu Z T,et al. A study on low strain integrity testing of platform-pile system using staggered grid finite difference method[J]. Soil Dynamics and Earthquake Engineering,2014,67:345-352.

[5]阙仁波,王奎华. 考虑土体三维波动效应时黏性阻尼土中桩的纵向振动特性及其应用研究[J]. 岩石力学与工程学报,2007,26(2):381-390.

[6]骆文和,闫启方.考虑桩-土相互作用的粘弹性土中管桩的纵向动力阻抗分析[J]. 昆明理工大学学报:理工版,2010,35(5):28-32,36.

[7]李魁彬,王安稳,胡明勇,等. 确定Kelvin模型粘弹性材料参数的一种实验方法[J]. 海军工程大学学报,2007,19(6):26-29.

[8]杨冬英,王奎华,丁海平. 三维非均质土中粘弹性桩-土纵向耦合振动响应[J]. 土木建筑与环境工程,2011,33(3):80-87.

[9]Higdon R L. Absorbing boundary conditions for difference approximations to the multi-dimensional wave equation[J]. Mathematics of Computation,1986,47(176):437-459.

[10]段军,刘东甲,程晓东,等.桩的一维纵向振动问题的交叉网格有限差分法数值计算[J].工程地球物理学报,2008,5(1):54-59.

[11]柯宅邦,刘东甲.低应变反射波法测桩的轴对称问题数值计算[J].岩土工程学报,2006,28(12):2111-2115.

(责任编辑胡亚敏)

Numerical calculation of transient vibration of large diameter integrate pile in three-dimensional viscoelastic soil

ZHANG Jian1,LIU Dong-jia1,LU Zhi-tang2,JIANG Jing1,GENG Xiao1,GAO Zi-jie1

(1.School of Resources and Environmental Engineering, Hefei University of Technology, Hefei 230009, China； 2.Dept. of Geotechnical Engineering, Tongji University, Shanghai 200092, China)

Abstract:In order to conduct low strain numerical simulation of pile, the pile-soil is considered to be viscous-elastic, and a three-dimensional pile-soil system transient vibration calculation model is established. The staggered grid finite difference method is used to solve three-dimensional viscous-elastic wave equation, and the absorbing boundary is introduced, then the dynamic vibration of complete pile under transient vertical excitation force is achieved. Pile-soil viscous-elastic parameters are analyzed by comparing the vibration velocity responses at pile top while different viscous-elastic parameters are given under three-dimensional conditions. The curves of different pick-up positions on pile top are simulated to get the best pick-up location of large diameter pile under viscous-elastic conditions, which reflect the characteristics of wave propagation in the pile directly and have guiding significance to engineering practice.

Key words:viscoelastic material; finite difference method; three-dimensional pile-soil model; absorbing boundary; best pick-up position

中图分类号:TU473.16

文献标识码：A

文章编号：1003-5060(2016)02-0211-06

Doi:10.3969/j.issn.1003-5060.2016.02.013

作者简介：张健(1991-),男,陕西蒲城人,合肥工业大学硕士生;刘东甲(1957-),男,安徽枞阳人,合肥工业大学教授,硕士生导师.

基金项目：广东省公路管理局资助项目(粤公研2011-21)；安徽省高速公路控股集团有限公司资助项目(AHGS2013-3)

收稿日期：2014-11-26；修回日期：2015-01-09