运营环境下输电导线径向温度分布模拟

周华敏，肖　凯，陈志为，刘永斗，李鹏云

( 1．广东电网公司电力科学研究院，广东广州510080; 2．厦门大学建筑与土木工程学院，福建厦门361005)



运营环境下输电导线径向温度分布模拟

周华敏1，肖凯1，陈志为2*，刘永斗2，李鹏云1

( 1．广东电网公司电力科学研究院，广东广州510080; 2．厦门大学建筑与土木工程学院，福建厦门361005)

摘要:细致分析运营中输电导线的温度场，对于实现提高输电线路载流量的目标具有重要意义．本文基于二维稳态热传导控制方程形成一套求解运营中输电导线径向温度分布的新方法，该方法考虑了导线的主要热源和散热途径，以及影响导线径向温度分布的多项因素．通过钢芯铝绞线的数值算例，验证了导线径向温度差的真实存在且不可简单忽略，并讨论了载流量、对流条件和铝绞线接触状态等因素对运营中输电导线径向温度分布的影响．

关键词:输电导线;运营环境;径向温度;数值模拟

随着我国经济的快速发展，生活和工业用电量激增，电网输电能力不足的问题日益突出．目前提高高压架空输电线路载流量主要是通过静态提温增容或动态监测增容技术实现［1－4］．由于导线的温度会影响其热膨胀变形，进一步会影响到允许载流量值，准确掌握运营环境下输电导线的温度，是该研究的关键也是难点．一方面，导线温度除了受电流载流量，还受日照、对流、辐射等众多外界因素的影响［5－7］;另一方面，大量的室内外实验测量了通电负载时张拉状态下导线的径向温度［8－12］，结果表明导线内部温度并非均匀分布．Douglass等［8］的试验结果表明导线的径向温度差高达5～15℃，导线中心与表面的温度差约为导线从周围环境温度温升的10%．IEEE规范［13］对导线内存在的径向温度差也进行了讨论，发现当电流密度小于1 A/ mm2时，导线径向温度差通常不会超过5℃;若电流密度更大时，特别是具有三或四层铝绞线的导线，径向温度差可达10～25℃．此外，钢芯铝绞线内存在的温度差较同尺寸全铝或全铜导线的温度差更大［9］．

20世纪末，已经开展了典型导线径向温度场的相关研究［14－15］，但它们在计算分析时，对模型做了较多简化，例如建立导线模型时，Black等［14］和Morgan［15］不计绞合导线内部每股钢芯和铝绞线层间的距离，假设芯体和外铝层分别为均质圆柱体和均质中空圆柱体，两层之间紧密接触，仅仅通过设置有效径向热导率来综合考虑复杂的导线内部结构的影响．因此，该类方法计算结果的准确性很大程度上依赖于有效热导率的取值合理与否，但是有效热导率的推荐值波动较大，合理范围可在0．5～4 W/( m·s)之间［13－16］．近年来，随着有限元技术的完善和计算机能力的提高，涌现了一些基于有限元模拟导线径向温度场的新方法［17－19］．但现有的数值模型过于简化，没有考虑铝绞线夹层中的空气对整体温度场的影响;同时，铝绞线整体与外界空气的热交换系数是铝绞线温度和环境温度的函数，文献中对该部分的影响讨论较少．目前，鲜有导线径向温度场研究综合考虑截面内空隙分布、铝绞线间接触以及空气对流条件等的影响．

因此，本文基于二维稳态热传导方程，提出一套模拟运营环境下输电导线径向温度分布的新方法，该方法不仅考虑了电流发热、日照发热、对流散热、辐射散热等影响导线平均温度的因素，同时还分析了导线内部各股铝绞线的外观、层数分布和铝绞线间接触面积等因素对导线径向温度分布的影响．首先，讨论了影响运营中输电导线平均温度和径向温度差异的主要因素;然后，基于二维稳态热传导控制方程，考虑了输电导线主要的热源和散热途径，形成一套准确的输电导线径向温度场数值求解方法;最后，以特定型号的钢芯铝绞线为例，研究载流量、铝绞线接触状态、对流条件等因素对运营中输电导线径向温度分布的影响．

1　输电导线径向温度场的数值求解方法

1. 1二维稳态热传导控制方程

求解输电导线径向温度场时，假定导线电流、周围环境等因素在一段有限长度的导线内保持不变，故可以认为导线温度沿导线纵向方向保持不变．因此，可以将导线的温度分布由更复杂的三维问题简化成导线横截面内的二维问题，重点研究导线内不同股铝绞线的温度分布规律．根据上一节中关于影响运营中输电导线径向温度的主要因素的分析，在求解中考虑的因素包含电流发热、外界吸热与散热，以及铝绞线间的接触状况和空气间隙的分布．

由于输电导线内各股铝绞线间以及铝绞线与空气间隙的传热符合二维稳态热传导控制方程，故可建立导线在整个横截面区域Ω内的热平衡方程［19］

以及在导线边界Γ的散热平衡方程［19］

其中: T，xx、T，yy、T，x、T，y分别表示导线内二维温度场T对坐标x、y的二阶导和一阶导; k为金属或空气的导热系数，假定为各向同性;η是单位体积的发热率，在导线不同区域内可不同; qn是沿着导线外表面法线方向n的散热率; nx和ny为法线方向n沿x、y方向的分量;α为复合散热系数; Tsur、Ta分别表示导线表面温度和环境温度．

运用虚功原理，对式( 1)分部积分，引入式( 2)的边界条件可得:

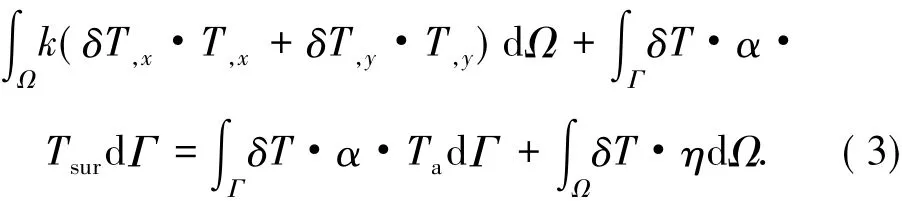
对式( 3)中铝绞线横截面的温度场根据形函数进行差值，将连续的热平衡方程进行空间离散，求解后可得到每个有限元单元节点上的温度值．

1. 2输电导线的热源与散热计算

钢芯铝绞线由于载电量大且性能稳定，被广泛应用于现有的输电线路［19］．鉴于不同导线的主要热源

和散热途径存在区别，本文以钢芯铝绞线为例，讨论导线的发热、散热和径向传热．图1为钢芯铝绞线的剖面图，导线外层采用铝绞线，内层采用钢芯材料．

图1钢芯铝绞线剖面图Fig．1 Cross section of steel－cored aluminium strands

钢芯铝绞线的热量来源由电流产生热量与吸收太阳能量两部分组成．钢芯位于导线内层，不直接受太阳光照射，故热量来源仅考虑电流发热．因钢芯和铝绞线的热量来源有所不同，式( 1)的单位体积发热率应分别计算．钢芯的单位体积发热率表示为

其中，Ast是钢芯的总截面面积; P是电流发热的总发热率，为导线载流量、导线平均温度和综合电阻率的函数［20］．单位长度的钢芯和铝绞线的电压相同，电流大小与电阻成反比，电阻的大小与导线截面积成反比，与电阻率成正比［21］．故钢芯电流Ist与铝绞线电流Ial的比值

其中，Aal是铝绞线的总截面面积，ρst和ρal分别是钢芯和铝绞线的电阻率．位于外层的铝绞线需考虑太阳光的辐射能［18］，故铝绞线单位体积发热率

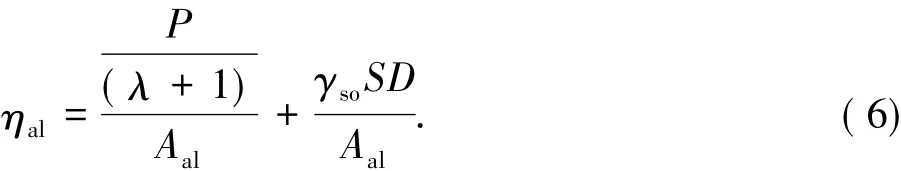
公式右端第2项是考虑太阳光辐射部分，其中: S为光照强度; D是导线的直径;γso为导线对光照的吸收率，取值在0．27～0．95，通常可取0．50．

根据体积散热率不变的原则，确定式( 2)中导线表面的复合散热系数［20］

其中:对流散热Pc和辐射散热Pr是导线最主要的2种散热方式; Tsur是导线表面平均温度; A是单位长度铝绞线的侧表面积．

1. 3径向温度场求解的计算流程

径向温度场求解的基本公式(式( 1)～( 2) )中的多个关键参数，如空气导热系数、钢芯和铝绞线的单位体积发热率、复合散热系数，均与导线平均温度或表面温度有关，故求解过程需先拟定温度初值，通过反复迭代稳定，方可确定导线径向温度场的真实值．该数值迭代求解的主要流程如下:

1)建立导线横截面的有限元几何模型;

2)设定导线温度场初始值Tin( n=0) ;

3)利用第n步的导线温度场Tin，求截面平均温度和边界平均温度;

4)求空气导热系数、单位体积发热率和复合散热系数;

5)引入自然边界条件(见式( 2) )，求第n+1步的温度场Tin+1;

2运营中输电导线径向温度分布的影响因素

2. 1钢芯铝绞线的有限元建模

以LHA2/LB1A－227/10型钢芯铝绞线为例，该导线由1根钢芯和2层18根铝绞线组成，图2( a)是导线的标准剖面图．根据该型号导线的几何参数(详见表1)，建立如图2( b)所示的导线有限元模型图．采用三角形实体单元划分模型网格，单元最大尺寸0．3 mm，整个模型共有11 236个单元，5 889个节点．

2. 2载流量对导线径向温度分布的影响

为了研究载流量因素对通电导线径向温度场的影响，选择LHA2/LB1A－227/10型钢芯铝绞线，同样处于自然对流条件(无风的理想条件)，逐渐改变通电导线的载流量．导线的交流电载流量从160 A逐步增加到660 A，电流增量为100 A．设置基本计算参数如下:钢芯和铝绞线的电阻率分别为ρst= 20×10－8Ω·m 和ρal=3．253×10－8Ω·m;钢芯导热系数kst= 80 W/ ( m·℃)，铝绞线导热系数kal= 237 W/( m·℃) ;光照强度S = 300 W/m2．还有一些参数与导线平均温度或表面温度相关，例如空气导热系数、钢芯和铝绞线的单位体积发热率、复合散热系数，需要通过1．3节中的数值方法迭代求解确定．

在自然对流条件下，载流量为360 A，LHA2/ LB1A－227/10型钢芯铝绞线的径向温度分布如图3所示．结果显示:导线最高温度出现在钢芯和里层铝绞线，外层铝绞线的温度较低，最高、低温度差约为4℃．其原因主要有: 1)铝绞线外层与空气对流边界直接进行热交换，故散热效率高，且该层温度较导线里层更低; 2)该型号导线的钢芯和铝绞线单线直径相同，热量能很好地通过金属间传递，故钢芯和里层铝绞线的温度基本一致．

图2 LHA2/LB1A－227/10型钢芯铝绞线(单位: mm)Fig．2 LHA2/LB1A－227/10 type steel－cored aluminium strand( unit: mm)

表1 LHA2/LB1A－227/10型钢芯铝绞线的几何参数［21］Tab．1_ Geometry parameters of LHA2/LB1A－227/10 type steel－cored aluminium strand［21］

__227．0　 12．6　 239．6　 18　1　4．0　4．0　4．0　 20．0

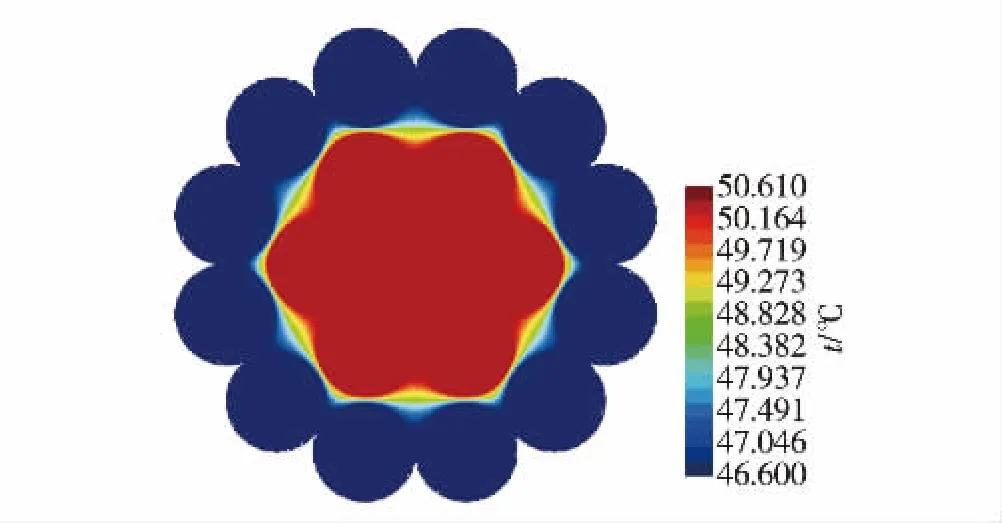
图3自然对流下LHA2/LB1A－227/10型导线径向温度分布Fig．3 The temperature of LHA2/LB1A－227/10 type steel－cored aluminium strand under natural convection

为了得到自然对流下导线径向温度分布的关键参数与载流量之间的关系，计算载流量从160 A逐步增加到660 A，研究的关键参数包括钢芯层和铝绞线层的单位体积发热率、复合散热系数、最高温度、最低温度和温度差，将所有结果整理列于表2用于比较．从表中可发现: 1)在不同载流量下，铝绞线层的单位体积发热率均明显大于钢芯层，这主要是由于2种材料金属有不同的面积和电阻率导致; 2)随着载流量的增加，电流发热的热量更多地在导线内积聚，导线温度(最高温度和最低温度)整体上升，并且由于与环境温度间的温度差增大，引起复合散热系数也相应增大; 3)随着载流量的增加，导线径向的最大温差有显著增长趋势，当载流量660 A时，温差甚至达到13．38℃．温差显著增大的原因一方面是载流量增加导致导线表面温度与环境温度的差距加大;另一方面是导线内部存在空气间隙等热不良导体，传热效率低且不均匀．

2. 3对流条件对导线径向温度分布的影响

自然对流和强制对流是导线2种主要的对流散热方式．在自然对流(风速vw= 0)下，被加热的空气上升并带走热量;在强制对流(风速vw≠0)下，热量主要是被流动的风所带走．真实运营环境下的输电导线需要考虑风所带来的空气流动的影响．为了研究不同的对流条件对导线径向温度分布的影响，保持温度场计算的其他计算参数不变，取强制对流条件下的风速vw= 0．6 m/s，风向δ= 30°．努赛尔数是空气动力学中反映对流传热强弱的无量纲数，因自然对流与强制对流条件下的努赛尔数取法不同，本研究考虑风向修正后的风速确定强制对流条件下的努赛尔数．

根据径向温度场的求解计算流程，得到不同的载流量在强制对流条件下导线径向温度分布的关键参数(见表3)，与自然对流条件下的结果(表2)相比较可以发现:强制对流条件下的复合散热系数明显高于自然对流条件下的结果，并导致前者的导线温度(最高温度和最低温度)明显低于后者．图4分别比较了2种对流条件下对应不同载流量的最高温度、最低温度和最大温差．从结果可以发现: 1)无论是在自然对流还是强制对流下，随着载流量的增大，导线的最高温度、最低温度以及最大温差都呈非线性增长，且增长速度逐渐加快; 2)强制对流降低了导线的整体温度，载流量越大，趋势越明显，但是对最大温差影响很小，2种对流条件的最大温差基本保持一致．

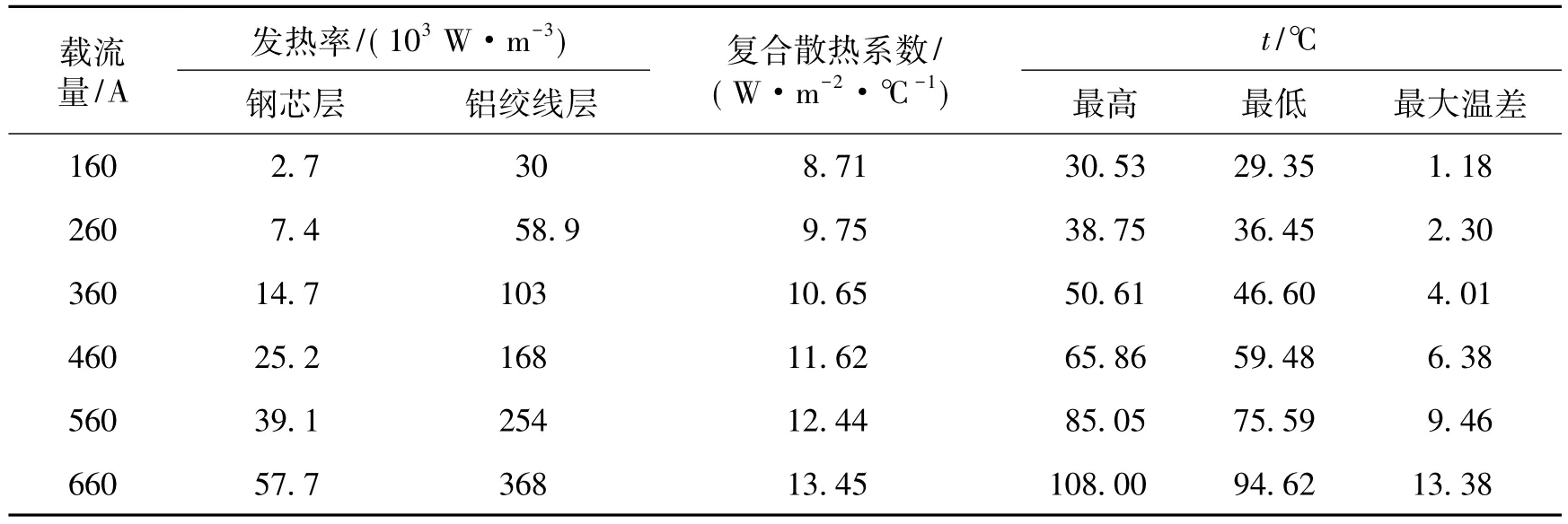
表2自然对流下导线径向温度分布的关键参数与载流量关系Tab．2 Relationship of radial temperature distribution parameters in natural convection and ampacity

2. 4绞线接触状态对导线径向温度分布的影响

为了讨论导线内各股绞线间的接触状况对导线径向温度分布的影响，以JL/LB1A300/50型钢芯铝绞线为例开展研究．图5是该型号钢芯铝绞线的标准剖面图，导线由中间2层7根钢芯和外面2层18根铝绞线组成，钢芯和铝绞线的单线直径分别为2．99和3．85 mm，导线的其他几何参数见表4．相比LHA2/ LB1A－227/10型导线，JL/LB1A300/50型导线内各股铝绞线的接触状况更复杂，首先钢芯和铝绞线各有2层，另外钢芯和铝绞线有不同的单线直径．

表3强制对流下导线径向温度分布的关键参数与载流量关系Tab．3 Relationship of radial temperature distribution parameters in forced convection and ampacity

图4导线温度与载流量的变化规律Fig．4 Relationship between conduct temperature and ampacity

图5 JL/LB1A300/50型钢芯铝绞线的标准剖面图(单位: mm)Fig．5 Cross section of JL/LB1A300/50 type steel－cored aluminium strand ( unit: mm)

同样基于上述通电导线径向温度场的求解流程，计算导线在自然对流条件下的径向温度分布．输入的基本参数包括:交流电载流量Iac=500 A，直流电阻Rdc=0．091 6 Ω/km，钢芯和铝绞线的电阻率为ρst= 20× 10－8Ω·m和ρal=2．8×10－8Ω·m，钢芯导热系数kst= 80 W/( m2·℃)，铝绞线导热系数kal= 237 W/( m2·℃)，光照强度S=900 W/m2．程序反复迭代稳定后，得到图6( a)所示导线径向温度分布图．进一步研究载流量、对流方式与JL/LB1A300/50型导线温度场分布的关系，可得到与上述2．2节和2．3节类似的结论．由此表明不同型号的钢芯铝绞线，虽截面尺寸、内部组成结构不同，但其温度分布规律一致，结论具有一定的普遍性．除此之外，还发现导线最高温度出现在内层铝绞线，使最里层的钢芯温度次之，最低温度出现在外层铝绞线．原因主要有: 1)铝绞线的单位体积发热率远大于钢芯，故热量相对较高，并有一部分热量传递给里层的钢芯; 2)最里层的钢芯离空气对流边界较远，再加上导线内存在空气间隙等热不良导体，故散热较慢，温度也相对较高; 3)铝线外层虽产生较多热量，但由于与空气对流边界直接进行热交换，故温度最低．另外，从图中还发现铝绞线外层不同股绞线间有明显的温度差异，主要原因是导线内各股铝绞线间的实际接触情况不同，导致局部有不同的孔隙率和孔隙分布，这会影响到传热路径与传热效率．实际上，各股铝绞线间实际接触位置与接触面积的变化对径向温度场会产生一定影响．为了研究该影响，保持其他条件不变，若将最外层铝绞线顺时针旋转180°，将导致里外2层铝线的接触点发生变化．新状态下的导线模型径向温度分布图绘于图6( b)．综合图6( a)、( b)结果，当相邻2层铝绞线间孔隙较小或紧密接触时，有利于热量及时从内层传递到外层，否则热量将集聚在内层，导致该层某根铝绞线局部温度较高．

表4 JL/LB1A300/50型钢芯铝绞线的几何参数［21］Tab．4 Geometry parameters of steel－cored aluminium strand ( JL/LB1A－300/50)［21］

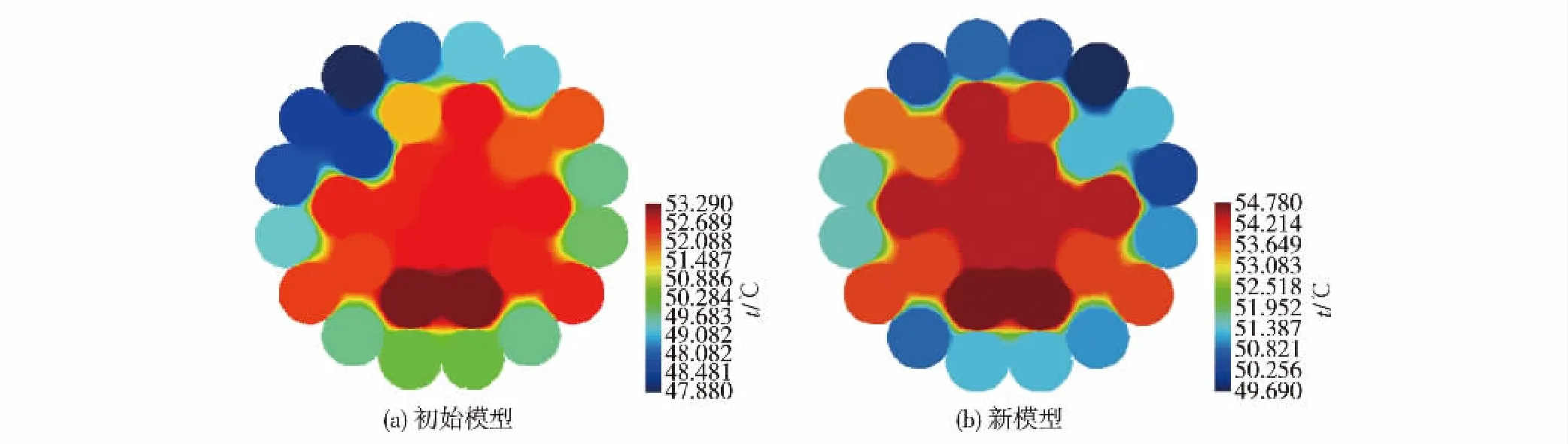
图6 JL/LB1A300/50型导线径向温度分布图Fig．6 Radial temperature distribution of JL/LB1A300/50 type steel－cored aluminium strand: ( a) original model; ( b) new model

3结论

本文基于二维稳态热传导控制方程形成一套求解运营中导线径向温度分布的方法，考虑了导线主要热源和散热途径，以及影响导线径向温度分布的多项因素．并且通过钢芯铝绞线的数值算例，讨论了载流量、对流条件和绞线接触状态等因素对运营中输电导线径向温度分布的影响，得到适用于钢芯铝绞线的主要结论:

1)随着载流量的增大，导线的最高温度、最低温度以及最大温差都呈非线性增长，且增长速度加快;

2)相比自然对流，强制对流并没有改变导线径向温度分布规律，但对流风更有利于导线散热，故导线整体温度会明显下降;

3)各股铝绞线间实际接触位置与接触面积的变化对径向温度场会产生一定影响．当相邻两层铝绞线间孔隙较小或紧密接触时，有利于热量及时从内层传递到外层，否则热量将集聚在内层，导致该层某根绞线局部温度较高．

参考文献:

［1］林玉章．高压架空输电线路载流量和温度计算［J］．南方电网技术，2012，6( 4) : 23－27．

［2］张辉，韩学山，王艳玲．架空输电线路运行载流量分析［J］．电网技术，2008，32( 14) : 31－35．

［3］任丽佳，盛戈皞，李力学，等．动态确定输电线路输送容量［J］．电力系统自动化，2006，30( 17) : 45－49．

［4］金珩，王之浩．输电线路动态监测增容技术［J］．华东电力，2005，33( 7) : 30－31．

［5］徐青松，季洪献，候炜，等．监测导线温度实现输电线路增容新技术［J］．电网技术，2006，30( S1) : 171－176．

［6］彭向阳，周华敏，郑晓光．架空运行线路现场载流温升试验研究［J］．南方电网技术，2008，2( 6) : 62－83．

［7］彭向阳，林一峰．环境风速对架空输电线路载流及温升影响试验研究［J］．广东电力，2012，25( 3) : 20－25．

［8］DOUGLASS D A，KIRKPATRICK L A，RATHBUN L S．AC resistance of ACSR－magnetic and temperature effects［J］．IEEE Trans on Power Apparatus and System，1985，5( 6) : 1578－1584．

［9］MORGAN V T．Rating of Bare conductors for continuous currents［J］．Proceedings of the Institution of Electrical Engineers，1967，114( 10) : 1473－1482．

［10］MORGAN V T．A theoretical and experimental analysis of the factors which determine the thermal behavior of a cylindrical current－carrying conductor［D］．London: University of London，1971．

［11］DOUGLASS D A．Radial and axial temperature gradients in bare stranded conductor［J］．IEEE Trans on Power Delivery，1986，1( 2) : 7－15．

［12］FOSS S C，LIN S H，CARBERRY R．Significance of the conductor radial temperature gradient within a dynamic line rating methodology［J］．IEEE Trans on Power Delivery，1987，2( 2) : 502－511．

［13］IEEE Power Engineering Society．IEEE standard for calculating the current－temperature relationship of the bare overhead conductor［M］．New York: The Institute of Electrical and Electronics Engineers Inc．，2013．

［14］BLACK W Z，COLLINS S S，HALL J F．Theoretical model for temperature gradients within bare overhead conductors ［J］．IEEE Trans on Power Delivery，1988，3( 2) : 707－715．

［15］MORGAN V T．The radial temperature distribution and effective radial thermal conductivity in bare solid and stranded conductors［J］．IEEE Transaction on Power Delivery，1990，5( 3) : 1443－1452．

［16］STEPHEN R，PIROVANO G，TUNSTALL M J．The thermal behaviour of overhead conductors，section 1: mathematical model for evaluation of conductor temperature in the steady state［J］．Electra，1997，22( 12) : 107－116．

［17］ZUNEC M，TICAR I．Determination of current and temperature distribution in overhead conductors by using electromagnetic－field analysis tools［J］．IEEE Transactions on Power Delivery，2006，21( 3) : 1524－1529．

［18］赵成运，郑良华．66 kV架空输电线路温度场的数值研究［J］．电网技术，2007，31( S2) : 34－36．

［19］梁盼望，何整杰，李震彪．输电线温度及载流量的ANSYS计算方法［J］．浙江电力，2010( 8) : 1－5．

［20］CIGRÉ．The thermal behavior of overhead conductors［R/ OL］．1992: 107－125．［2015－01－20］．http:∥www．e－cigre．org/Publications/file．asp．

［21］中华人民共和国国家质量监督检疫总局．圆线同心绞架空导线: GB/T 1179—2008［S］．北京:中国标准出版社，2008．

·研究简报·

Numerical Simulation on Radial Temperature Distributions of Operational Transmission Conductors

ZHOU Huamin1，XIAO Kai1，CHEN Zhiwei2*，LIU Yongdou2，LI Pengyun1

( 1．Guangdong Power Grid Corporation Co．Ltd．，Guangzhou 510080，China; 2．School of Architecture and Civil Engineering，Xiamen University，Xiamen 361005，China)

Abstract:Because we desire to increase the ampacity of operational transmission line，it is critical to accurately analyze temperature fields of conductors．This study proposes a new method for radial temperature distribution analyses of operational transmission conductors based on 2－D steady－state heat conduction control functions．In addition to main heat gains and heat losses of conductors，this method also considers key factors which influence radial temperature distributions．Numerical cases of aluminum conductor steel reinforced ( ACSR) conductor are studied，and we have proved that the existence of temperature differences in radial direction of conductors cannot be simply neglected．Furthermore，effects of ampacity，convection condition，and contact condition among strands on radial temperature distribution of operational transmission conductors are also discussed．

Key words:transmission conductor; operational environment; radial temperature; numerical simulation

*通信作者:cezhiwei@ xmu．edu．cn

基金项目:广东电网公司科技项目( K－GD2014－0596002－001)

收稿日期:2015－02－22录用日期: 2015－09－29

doi:10．6043/j．issn．0438－0479．2016．01．026

中图分类号:TM 751

文献标志码:A

文章编号:0438－0479( 2016) 01－0137－07

引文格式:周华敏，肖凯，陈志为，等．运营环境下输电导线径向温度分布模拟［J］．厦门大学学报(自然科学版)，2016，55( 1) : 137－143．

Citation: ZHOU H M，XIAO K，CHEN Z W，et al．Numerical simulation on radial temperature distribution of operational transmission conductors［J］．Journal of Xiamen University( Natural Science)，2016，55( 1) : 137－143．( in Chinese)