双驱双向AGV机器人运动学分析及仿真
2016-04-12KinematicsanalysisandsimulationofdoubledriveanddoubledirectionAGVrobot
Kinematics analysis and simulation of double-drive and double-direction AGV robot
王殿君1,关似玉1,陈 亚1,彭文祥1,王超星2
(1.北京石油化工学院 机械工程学院,北京 102617;2.北京化工大学 机械工程学院,北京 100029)
WANG Dian-jun1, GUAN Si-yu1, CHEN Ya1, PENG Wen-xiang1, WANG Chao-xing2
双驱双向AGV机器人运动学分析及仿真
Kinematics analysis and simulation of double-drive and double-direction AGV robot
王殿君1,关似玉1,陈亚1,彭文祥1,王超星2
(1.北京石油化工学院 机械工程学院,北京 102617;2.北京化工大学 机械工程学院,北京 100029)
WANG Dian-jun1,GUAN Si-yu1,CHEN Ya1,PENG Wen-xiang1,WANG Chao-xing2
摘要:针对双驱双向AGV机器人采用两个驱动模块的构型特点,利用四轮差速原理建立AGV机器人在转弯过程的运动学模型,运用ADAMS仿真软件对AGV机器人进行运动学仿真,并利用MATLAB软件对AGV机器人运动学模型进行数值分析,通过对比机器人理论计算和仿真结果的偏差,验证了运动学理论分析的正确性,为继续优化机器人结构设计、轨迹规划以及控制系统设计奠定了基础。
关键词:双驱双向AGV机器人;运动学模型;虚拟样机
0 引言
自动导引车(Automated Guided Vehicle,简称AGV)是智能搬运机器人的种,它主要依靠电磁、激光或磁条等导引装置,无需操作人员驾驶就能沿预定轨迹或导引路径行进,实现物料的智能搬运[1~3]。在自动化物流系统中,最能充分地体现AGV的自动化和柔性,实现高效、经济、灵活的无人化生产。同时,随着AGV性能的不断完善,其应用范围大为扩展,不仅将在工业、农业、国防、医疗、服务等行业中得到广泛的应用,而且将在搜索、救援、辐射和空间领域等有害与危险场合得到很好的应用。
1 双驱双向AGV机器人运动学模型的构建
1.1三维模型的建立
双驱双向AGV机器人的机械本体是由车体、驱动模块、牵引模块以及辅助运动模块等组成。采用UG软件建立了AGV的维模型如图1所示。AGV的行走机构由四个向轮、两个驱动模块组成,按中心对称布置,每个驱动模块包括两个驱动轮。机器人的直线和转弯行走主要通过驱动模块来实现,AGV机器人可以按照预设的轨迹路线进行作业,实现在不同复杂工况下的预设搬运任务。

图1 双驱双向AGV机器人三维模型
1.2运动学模型的建立
在对双驱双向AGV机器人进行运动学建模之前,先作如下假设:
1)AGV由刚性构架组成;
2)运动平面平整光滑,且只作无滑移纯滚动运动;
3)车轮与地面摩擦小到不足以影响车轮沿自身旋转轴线转动。
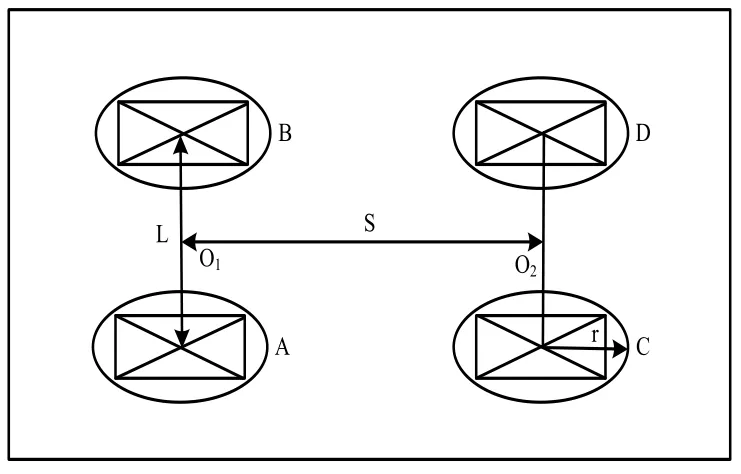
图2 双驱双向AGV机器人结构简图
当AGV机器人沿着铺设的磁条直线行走时,两个驱动模块的四个驱动轮速度相等;当AGV机器人转弯行走时,要通过两个驱动模块的协调以及AGV机器人自动循迹运动来实现。将双驱双向AGV转弯过程抽象为个阶段,如图3所示。

图3 转弯过程运动简图
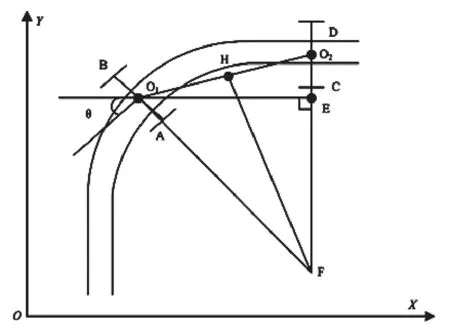
图4 转弯第一阶段
O1点速度为:


由图4可知,在ΔFHO2中,,进步化简得:
综上所述,双驱双向A G V最小转弯半径为Rmin=737mm/1.414=521mm。
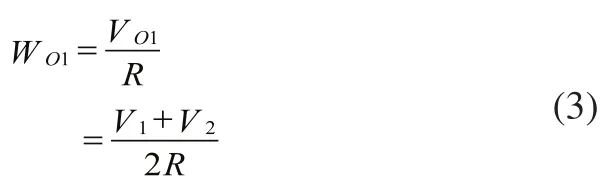
由于刚体运动时刚体上各点角速度相等,则O2点角速度为:

设t1时刻两个驱动模块瞬时运动半径为R',O2点瞬时速度为:

在ΔFO1O2中,,在ΔFHO2中,,代入公式(5)可得:

由于第二个驱动模块沿着磁条做直线运动,可以得出C、D轮速度为:

2)AGV转弯第二阶段

图5 转弯第二阶段
设t2时刻两个驱动模块瞬时运动半径为磁条的铺设半径R,由式(3)~式(5)可以得出O2点速度为:
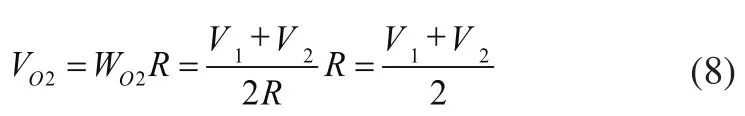
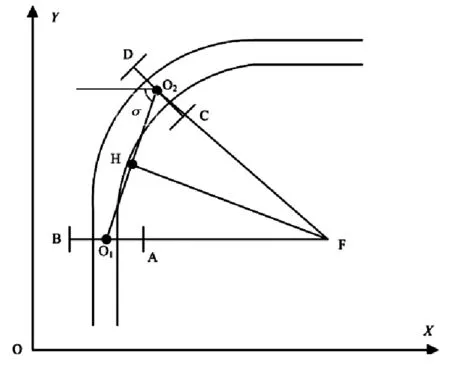
图6 转弯第三阶段
设经过时间t3,第二个驱动模块转过的角度与X轴夹角为D轮走过的弧长为,C轮走过弧长为,则C轮和D轮走过的弧长差为:
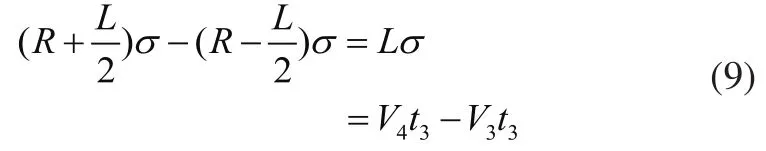
设t3时刻两个驱动模块的瞬时半径为R'',在ΔFO1O2中,则在ΔFHO1中:

此时C轮速度为V3,D轮速度为V4,则O2点速度为:

第二个驱动模块沿着磁带做圆周运动,则O2点角速度为:

两个驱动模块组合成刚体运动,刚体运动时角速度处处相等,则O1点角速度为:

O1点瞬时速度为:

联立式(10)、式(13)与式(14)可知O1点瞬时速度为:
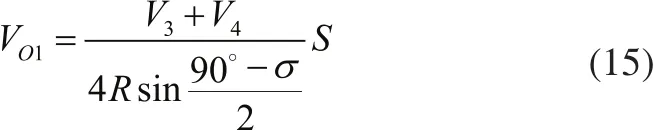


表1 AGV转弯过程各驱动轮瞬时速度
2 双驱双向AGV机器人运动学仿真
2.1仿真方案的确定
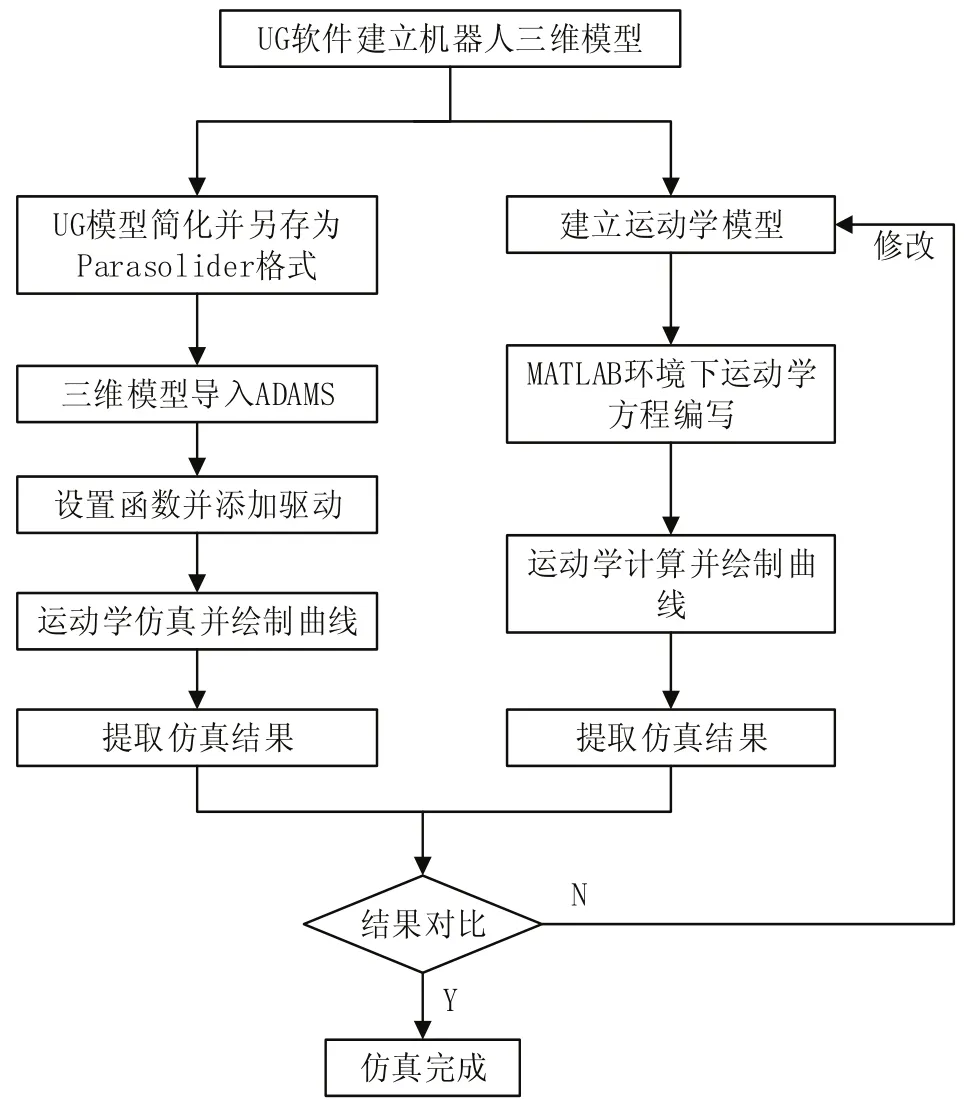
图7 运动学仿真技术方案
2.2虚拟样机的建立

图8 ADAMS中的双驱双向AGV机器人虚拟样机
模型导入后首先将不需要仿真的AGV部件运用固定副连接起来使之不能相对运动,然后对四个向支撑轮和四个驱动轮创建旋转副,并把剩余的部件运用相应的运动副连接起来,最后在各个车轮和地面之间建立接触。
将虚拟样机中的各个部分连接好后,需要在四个驱动轮上添加驱动。由于驱动模块上有个弹簧提供给驱动模块正压力,所以还需要在驱动模块和车架之间添加弹簧,然后将弹簧系数设置为15N.mm,并添加预紧力[8~10]。经过上述操作,使得AGV虚拟样机能够在设置的平面上顺利行走。
2.3运动学仿真与分析
为了完整地仿真AGV的行走特性,设定AGV的行走过程为:先让AGV走段直线,控制AGV左转弯,然后再让AGV走段直线,再左转弯,反复运动,AGV共完成四个弯道。将AGV仿真过程分为四部分,每个部分包括直线行走以及转弯行走个阶段,共16个运动阶段,每个驱动轮需要编写16个STEP函数,根据AGV各个驱动轮瞬时速度方程,计算各个阶段临界点速度,编写四个驱动轮的STEP函数。
在图10中,每个驱动模块的位移曲线在X、Z方向的同步变化反应了AGV的行走状态。两个驱动模块的位移曲线在X或Z方向的大小与趋势几乎没有偏差,说明AGV的两个驱动模块运行时轨迹重复,不会发生脱离磁条的情况。
2.4理论计算与仿真分析的对比
根据所推导出的AGV机器人运动学模型,采用ADAMS仿真中初始驱动轮的瞬时速度值及临界点的速度值,利用MATLAB编程并求解出AGV机器人第个驱动模块和第二个驱动模块中心点在X、Z方向的位移,将数据提取出来,再与ADAMS仿真得出的轨迹点绘于同图中,如图11~图14所示。

图9 双驱双向AGV虚拟样机行走轨迹
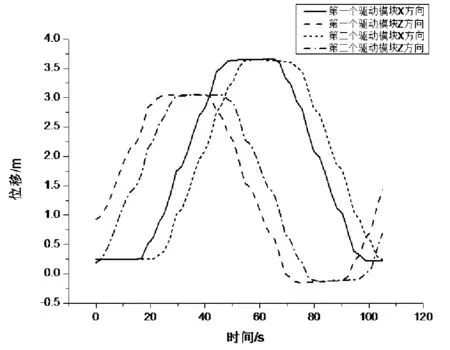
图10 ADAMS仿真中X、Z方向的位移曲线
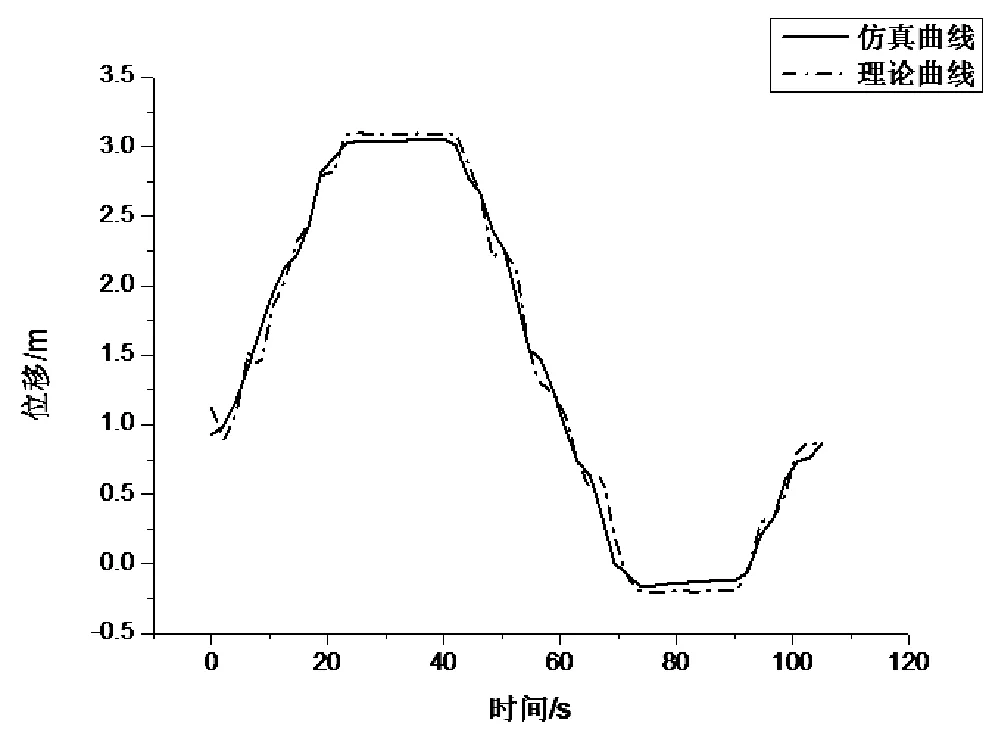
图11 第一个驱动模块中心在Z方向的位移

图12 第一个驱动模块中心在X方向的位移

图13 第二个驱动模块中心在Z方向的位移
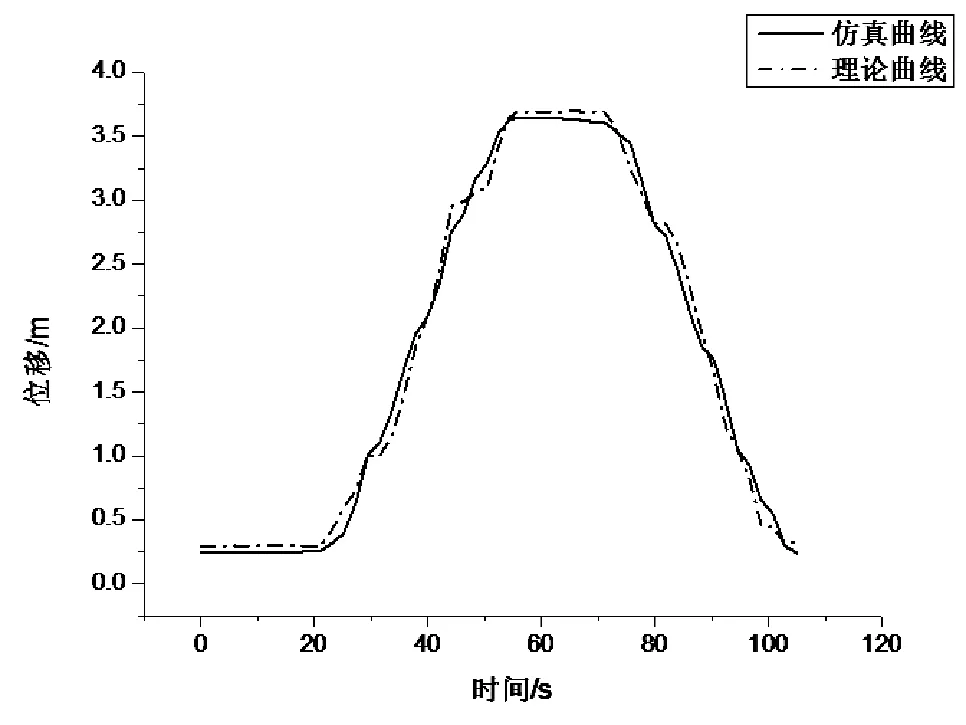
图14 第二个驱动模块中心在X方向的位移
通过仿真曲线与理论曲线的对比可知,AGV机器人的位移曲线存在偏差。这是由于AGV在转弯时受到诸多不确定因素的影响,如车体受到横摆角速度、侧倾力
【】【】
的影响,车轮侧偏角的不确定性等。但是偏差较小,平均偏差小于0.14m,在合理范围之内。同时,两者的曲线变化趋势大体相同,证明了双驱双向AGV机器人的理论计算和仿真分析的合理性及正确性。
3 结论
2)基于ADAMS软件仿真AGV机器人的直线与转弯过程,得到了相关运动参数的仿真曲线。基于MATLAB软件对运动学模型进行理论分析,得出理论曲线。
3)将AGV运动学模型的理论数据和仿真数据进行对比,其平均偏差较小,在合理范围内,说明了运动学理论分析的正确性。
4)本文所进行的运动学分析为双驱双向AGV机器人的结构优化设计、工作空间轨迹规划、通过性能分析等方面提供了重要的参考价值。
参考文献:
[1] 丁森,瞿文燕.双驱动AGV转弯分析与优化[J].计算机光盘软件与应用,2013,(04):203-204.
[2] 唐文伟.AGV在物流领域中的应用前景分析[J].物流技术,2001, 108(3):7-8.
[3] 李季.磁导引AGV的设计[D].济南:山东大学,2013.
[4] 王聪,王帅.AGV运动学模型及原理探析[J].科技资讯,2012, (07):67-69.
[5] 常勇,马书根,王洪光,等.轮式移动机器人运动学建模方法[J].机械工程学报,2010,46(5):30-36.
[6] 倪振.激光导引四轮差动全方位移动AGV关键技术研究[D].重庆:重庆大学,2013.
[7] 周驰东.磁导航自动导向小车(AGV)关键技术与应用研究[D].南京:南京航空航空大学,2012.
[8] 李进,陈无畏,李碧春,王檀彬.自动导引车视觉导航的路径识别和跟踪控制[J].农业机械学报.2008,39(02):20-24.
[9] 尹晓红.自动引导车运动分段控制技术研究[D].合肥:合肥工业大学,2011.
[10] 贺丽娜.AGV系统运行路径优化技术研究[D].南京:南京航空航天大学,2011.
作者简介:王殿君(1973 -),男,教授,博士,研究方向为机器人技术。
基金项目:北京石油化工学院URT项目(2014J00087)
收稿日期:2015-10-08
中图分类号:TP242.2
文献标识码:A
文章编号:1009-0134(2016)03-0042-05
