双臂喷釉机械手运动特性分析

Kinematics characteristics analysis of dual-arm glaze spraying manipulator

冯　浩，詹勇军

（景德镇陶瓷学院，景德镇 333403）

FENG Hao,　ZHAN Yong-jun



双臂喷釉机械手运动特性分析

Kinematics characteristics analysis of dual-arm glaze spraying manipulator

冯浩，詹勇军

（景德镇陶瓷学院，景德镇 333403）

FENG Hao,ZHAN Yong-jun

摘要：针对自主设计的双臂喷釉机械手，应用D-H法建立两个手臂局部坐标系，通过局部坐标系与全局坐标系的转换建立双臂机械手的运动学模型。提出以几何法为基础结合逆变换联合求解的方法，求解双臂喷釉机械手的运动学正逆解。在MATLAB环境中运用定步距角法对双臂机械手的工作空间进行求解。用Robotics Toolbox工具箱对机械手进行正逆运动学仿真，同时将各关节转角代入运动学方程进行求解并对比分析，从而验证机械手设计的合理性和运动学解的准确性, 为进一步研究奠定理论基础。

关键词：喷釉机械手；运动学正逆解；工作空间；定步距角法；Robotics Toolbox

0　引言

上世纪九十年代以来，喷釉机械手的研究和应用发展迅速，通过不断地技术革新，已经实现了工业化应用。例如：ABB公司开发出的五自由度喷釉机械手，同时结合旋转工作台组成喷釉系统；美国Nutro公司将直角型喷漆机械手造成适用于自动喷釉的生产线；意大利生产的喷釉机器人能快速的进行喷釉，并提高坯体的釉浆实际附着率等。与手工喷釉设备相比，机械手的生产效率更高，喷涂质量更稳定，同时还能有效的降低生产成本[1]。根据调查，目前的喷釉工序需要重复数次才能完成，导致单件产品的工时过长，不利于进步提高喷釉效率。由现有的文献资料可知，当前的研究主要集中于单臂喷釉机械手[2]，对双臂喷釉机械手的相关研究甚少，而双臂喷釉机械手在提高生产效率、双臂协作配合和数据通信等方面有着巨大的优势[3]，因此对双臂喷釉机械手的研究具有很强的现实意义。喷釉机械手的运动特性是其动力学分析、双臂协作、误差分析和离线编程等的基础，也是机械手研究和应用的重要内容。

1　双臂喷釉机械手结构简介

机械手的结构形式包括直角坐标型、关节型、圆柱坐标型和球坐标型[4]，其结构形式的选择取决于其工作范围、负载能力、精度要求和灵活性等。在这四种结构形式中，关节型机械手具有手臂活动范围大、空间姿态调整速度快、工作环境要求低和灵活性好等优势，因此是目前应用最广泛的结构形式。本文针对自主设计的关节型双臂喷釉机械手进行运动学分析，其结构主要由底座、立柱、顶部支撑回转机构、大臂回转机构、小臂回转机构、腕部旋转机构和喷枪等组成，左右手臂结构完全对称。机械手的两个手臂均具有5个旋转自由度，其中3个手臂自由度实现手臂的位置调整，另外2个手腕自由度实现机械手末端喷枪的姿态调整。

2　双臂喷釉机械手运动学分析

2.1D-H坐标系建立

为描述机械手相邻杆件间的位姿关系，文献[4]提出了D-H坐标法，其基本原理是为机械手每个关节处的杆件都建立个坐标系，然后用4×4的齐次变换矩阵来表示与前个杆件的位姿关系，通过齐次变换建立机械手的运动学方程，从而得出机械手末端在全局坐标系下的位姿。结合本文所分析的机械手参数和静止时的关节角度，建立双臂机械手的D-H坐标系如图1所示，其中每个关节的回转轴线均与Z轴重合，因此可以得出关节1轴线与立柱轴线平行，关节1和关节2的轴线垂直，关节3和关节4的轴线均与关节2平行，关节5与关节4垂直。机械手连杆参数如表1所示。

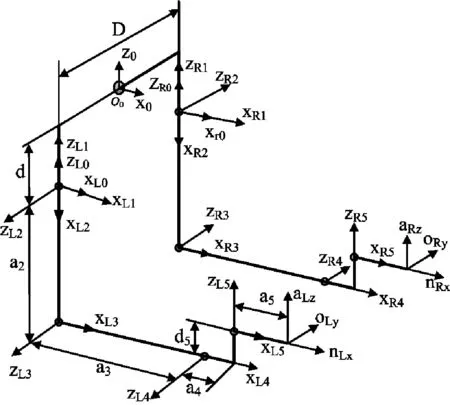
图1　双臂机械手D-H坐标系

表1　双臂机械手D-H参数表

在图1中，（x0, y0, z0）表示全局坐标系，（xL0,yL0,zL0）和（xR0,yR0,zR0）分别表示左、右手臂局部坐标系，其坐标原点均位于关节1与关节2轴线的交点上，两臂的局部坐标系相对于全局坐标系对称；参数D（D=600mm）为左、右臂之间的距离；ai表示机械手各连杆的长度，其中a2=1000mm，a3=760mm ，a4=83mm，a5=175mm；di表示相邻两连杆的偏移距离，其中d5=137mm。在表1中αLi、αRi分别表示左、右臂中相邻两坐标系的Z轴间的关节扭转角，θ1～θ5分别为对应关节的旋转角度。

2.2正运动学求解

机械手的正运动学问题是在已知各个关节转动角度和机械手杆件参数的前提下，求解机械手末端在全局坐标系中的位姿，其实质是运动学方程的建立和求解[5]。在机械手的实际应用中，般是已知机械手末端位姿反求每个关节的角位移，也就是机械手逆运动学问题。机械手正逆运动学之间的关系如图2所示。

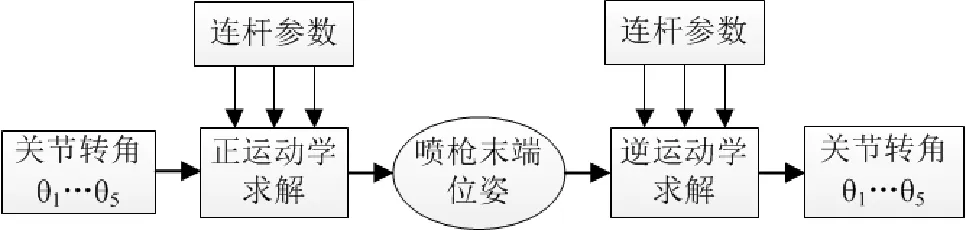
图2　正逆运动学关系

本文所研究的机械手关节均为转动关节，所以在运动学求解中用矩阵Ai表示机械手相邻杆件间的位姿关系，其Ai的转换通式为：

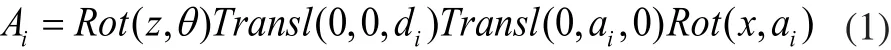
将式(1)展开得：

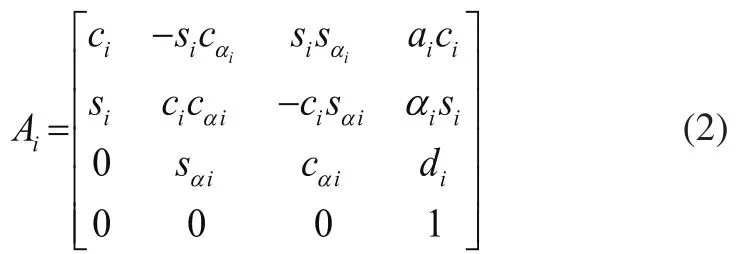
在正运动学求解过程中，任意杆件相对于机械手末端的位姿坐标关系可表示为：

现以求左臂的正运动学求解为例，将表1中的参数代入式(2)，由此可以推导得到每个连杆的变换矩阵：

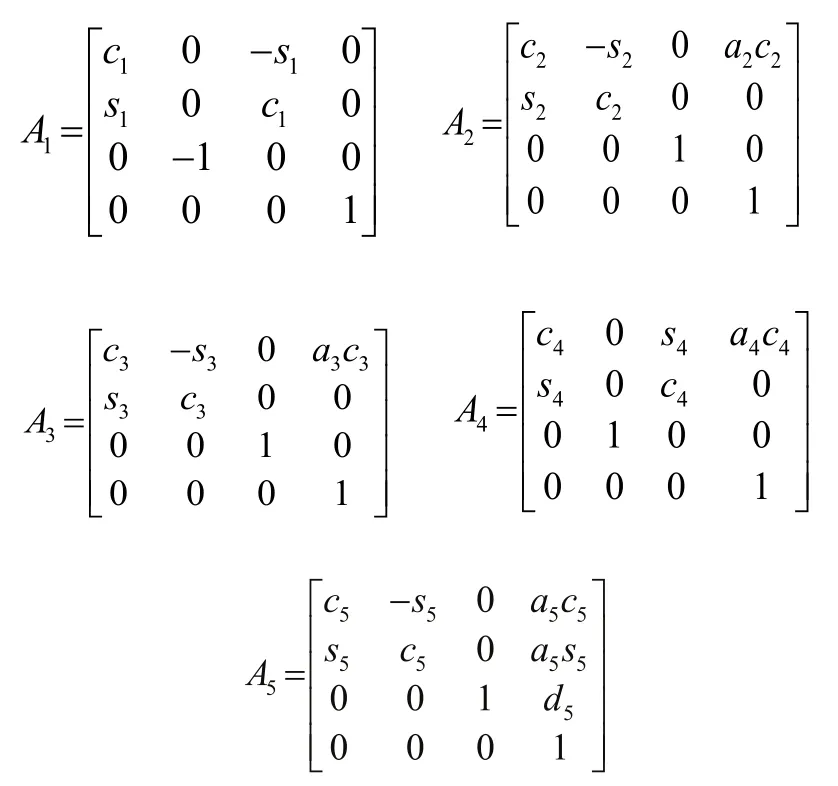
将连杆1到连杆5的齐次变换矩阵依次相乘得到其运动学方程如式(4)所示。

又：

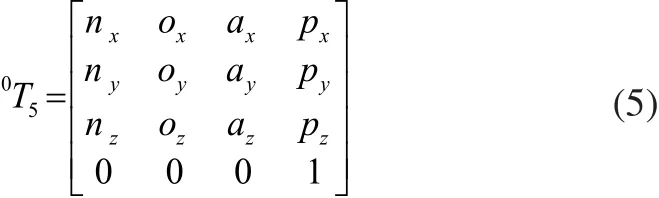
将各关节参数代入式(5)得到机械手左臂的正运动学解，同法可以求出机械手右臂的正运动学解。

2.3逆运动学求解

根据坐标变换，可以由机械手末端位置坐标[px,py,pz]求出关节5的坐标[p5x,p5y,p5z]，即：

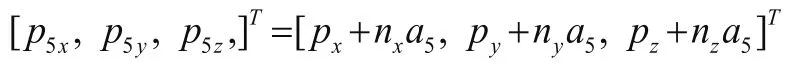
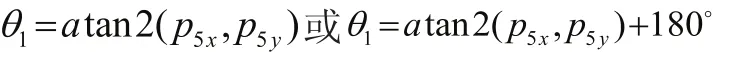
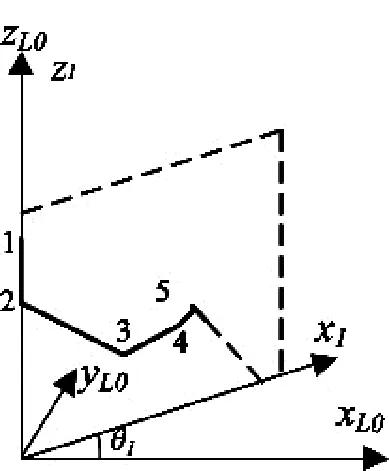
图3　连杆空间位置

在用几何法求得θ1的基础上，再利用反变换法求解θ2、θ3、θ4和θ5。首先求出每个关节的齐次变换矩阵的逆矩阵其次在运动学方程(4)的两边依次左乘得：

通过等式左右对应相等可以依次求出：

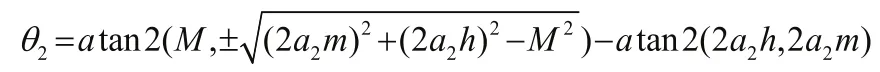
由上式可知θ2在45°～135°的范围内有两个不同的解。

其中：

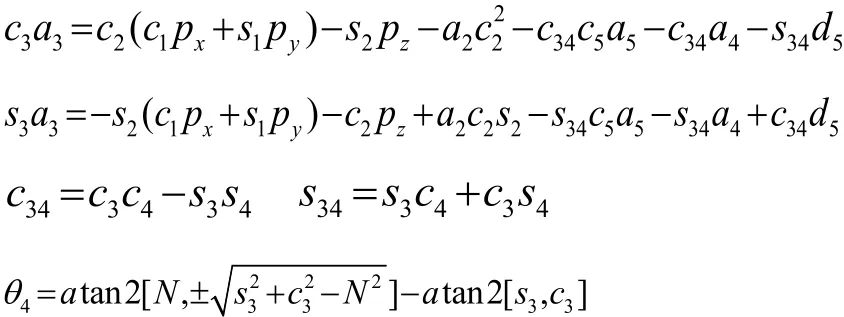
在高职院校的发展过程中，为了可以更好的培养学生的工匠精神，院校还应该对结合自身发展现状，对课程内容、课程设计等进行合理革新。

由上式可知θ4在-120°～120°的范围内有两个不同的解。

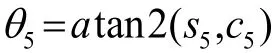
至此，我们就得到了关节1～5的运动学逆解。在求解过程中可得机械手存在多组解，根据机械手的实际需求，按照路径最短原则选择出最优解。

3　局部坐标系与全局坐标系转换

在双臂机械手的D-H坐标系中，其左右手臂的局部坐标系与全局坐标系的位姿关系如图1所示，根据坐标变换可以得出左右手臂的局部坐标系到全局坐标系的变换矩阵为，即：

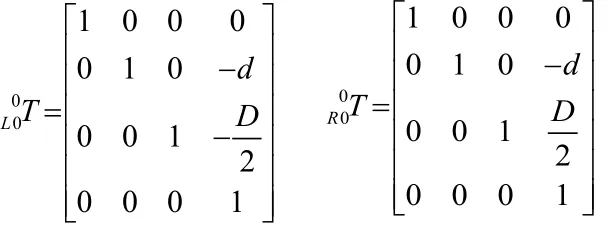
双臂喷釉机械手在执行喷釉任务时必须确定喷枪在全局坐标系下的位姿，因此须在手臂局部坐标系的基础上再次左乘。这样就可以在全局坐标系中确定喷枪的位姿，再根据逆运动学求解方法得出手臂的每个关节的转角。

4　机械手工作空间分析

工作空间是机械手的最大活动范围，是衡量机械手工作性能的重要指标。其研究方法主要包括数值法、图解法、解析法及仿真法等[7]。其中基于随机理论的蒙特卡洛法运用最为广泛，但其取值无规律，且只能在工作空间内部产生，因此不能清晰和完整的展现工作空间的边界轮廓。本文采用的定步距角法[8]，它在工作空间范围内按定规律取值，所求得的坐标点分布均匀，且其边界清晰完整。其求解步骤是：

根据求得的机械手正运动学解，求出机械手末端在全局坐标系下的位置坐标；

将所有的关节变量代入到式(5)，求出机械手末端喷枪相应的位置矢量值；

在实际应用中，机械手左右臂的工作空间有重叠，在重叠区内机械手双臂的运动会发生干涉，因此需要在重叠区对机械手进行协调规划来防止发生干涉。本文为了使仿真模型更为简化，在进行左右臂运动仿真时，将机械手的工作空间划分为左右对称的两个区域，左右臂各自在相应区域内进行仿真。

5　MATLAB仿真实验

在进行运动学仿真时，根据D-H参数表建立双臂机械手的仿真模型。通过Larm.teach()和Rarm.teach()就可以在Robotics Toolbox中显示双臂机械手的维模型，通过调节控制面板上的五个角度值，就可以自动计算出该手臂在其全局坐标系下的笛卡尔坐标位置和方向，并且驱动手臂的运动。

5.1手臂正运动学仿真验证

正运动学仿真过程就是在给定所有关节的转动角度前提下，通过仿真来求出喷枪末端的位姿。为验证正运动学分析的正确性，设计了通过角度值代入计算和利用Robotics Toolbox仿真进行对比的方案，通过对比分析能够更好的验证正运动学分析的正确性。逆运动学仿真分析过程与正运动学过程相反，其中正运动学仿真验证的流程如图4所示。

图4　正运动学仿真验证的流程图

本文以对机械手进行点到点的仿真为例，取机械手静止时的位姿作为初始位置，左臂的起点关节角为AL（0 ,pi/2, -pi/2, 0, 0），终点为BL（pi/4, pi/3,- pi/3,-pi/10,-pi/4）；右臂起点关节角为AR（0 ,pi/2, pi/2, 0, 0），终点为BR（-pi/4, pi/3,- pi/3,-pi/10,pi/4）。将左臂BL关节角代入正解位姿矩阵，求出左臂末端的位姿矩阵PL式(6)和右臂末端的位姿矩阵PR；同时在MATLAB中运用Robotics Toolbox进行正运动学仿真，仿真得到左臂末端位姿矩阵TRL如式(7)所示，左臂末端位姿矩阵TRR。现以左臂的仿真结果为例，对比两个矩阵，可以看出矩阵中元素存在的偏差约为4.1‰，同样可以得出右臂的偏差在4.4‰，从而验证了运动学正解的准确性。

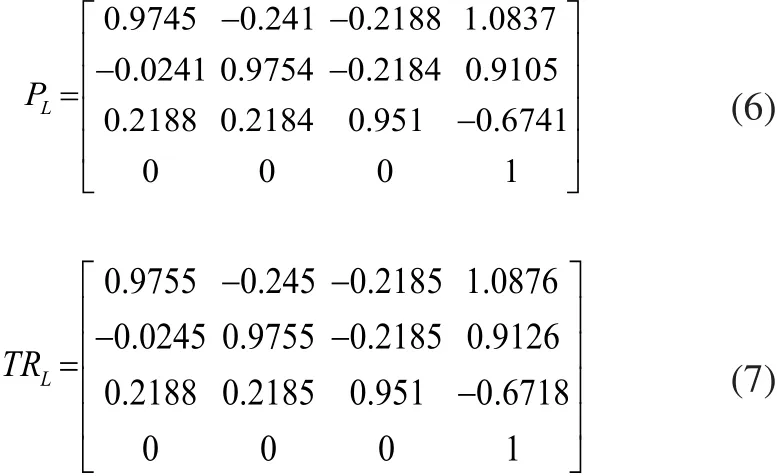
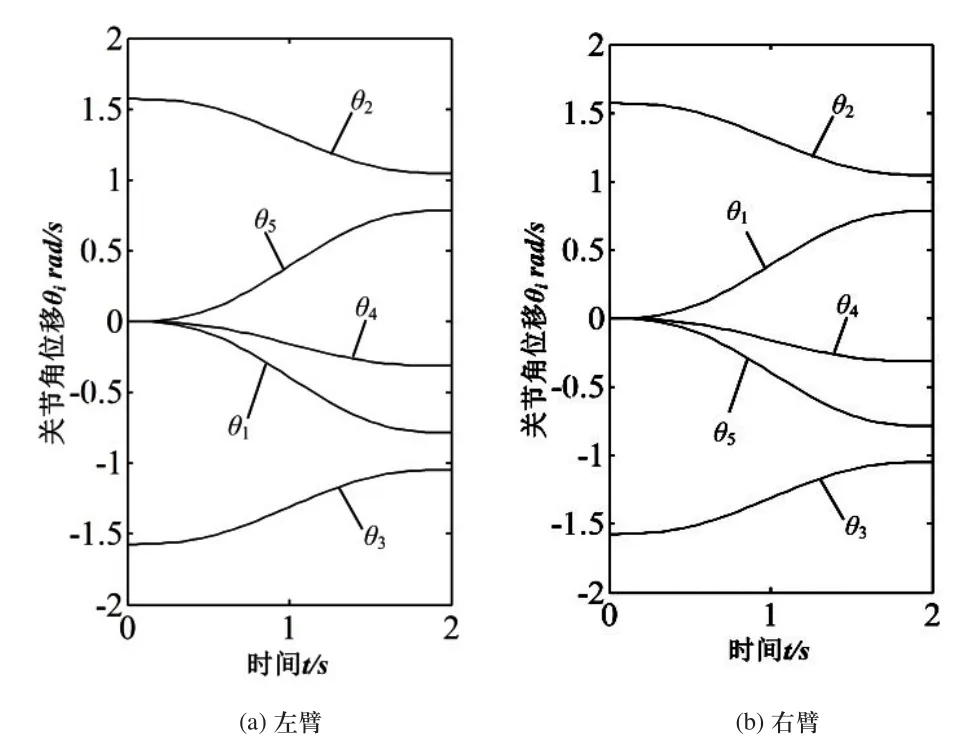
图5　双臂正运动学仿真关节角位移

由图5可知左右手臂在点到点的运动过程中角位移曲线平滑，可知运动平稳且相邻两杆没有错位，由此验证了机械手连杆设计的合理性和正解算法的准确性。

5.2逆运动学仿真分析

在逆运动学分析时，取左臂在正运动学仿真时的终点位置坐标AL（1087.6,912.6,-671.8）作为起点，取正运动学起点坐标BL（1018,0,-863）作为终点；同法取右臂的起点位置坐标AR（1087.6,-912.6,-671.8），以终点位置坐标BR（1018,0,-863）为例进行逆运动学仿真。用ctraj()函数来规划机械手末端的轨迹，并运用ikine()函数来规划各个关节的关节角位移，仿真间隔0.05s，时长2s，左右臂的关节角位移如图6所示。

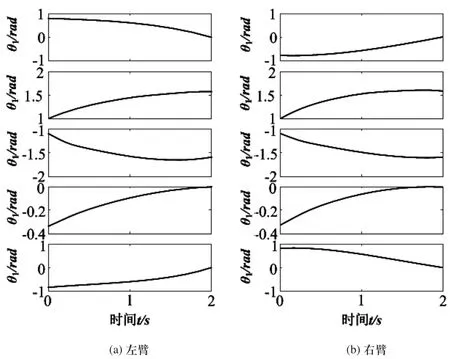
图6　双臂逆运动学仿真关节角位移

由图6可知，左臂由AL点运动到BL点所对应的关节角为（pi/4,pi/3,-pi/3,-pi/10,-pi/4），右臂AR点运动到BR点所对应的关节角为（-pi/4,pi/3,-pi/3,-pi/10,pi/4），而这两个关节角正好和正运动学分析时的关节角相等，验证了逆运动学求解的正确性，同时也验证了结构设计的合理性。对比图5和图6还可以得出，在正逆运动仿真中机械手关节的角位移变化过程不相同，这说明机械手逆运动学解具有不唯性。

6　结论

本文针对自主设计的双臂喷釉机械手，对其进行运动学建模和正逆运动学问题求解。在MATLAB环境中对双臂机械手的工作空间进行分析，并对双臂仿真时的工作空间进行划分。利用Robotics Toolbox工具箱对机械手进行运动学仿真，同时将各关节转角代入运动学方程进行求解，通过对比验证了正逆运动学求解的准确性和机械手设计的合理性。为机械手后续的动力学分析、双臂协作、误差分析以及离线编程等奠定理论基础，并对具有相似结构参数的机械手设计有定的参考意义。

参考文献：

[1] Schmidt D. The Use of Multiple Axes Robots in the Ceramics Industry[J].Interceram.2002,51(3):216-221.

[2] 王田苗,陶永.我国工业机器人技术现状与产业化发展战略[J].机械工程学报,2014,(9):1-9.

[3] J Lemburg,DGF José,M Eich,D Mronga,P Kampmann. AILA - Design of an autonomous mobile dual-arm robot[A]. IEEE International Conference on Robotics & Automation[C]. 2011,19(6):5147-5153.

[4] 蔡自兴.机器人学基础[M].机械工业出版社,2013(9).

[5] LU Yi , ;LI Xuepeng . Kinetostatics Analysis of a Novel 6-DOF Parallel Manipulator with Three Planar Limbs and Equipped with Three Fingers[J].Chinese Journal of Mechanical Engineering, 2014 ,(5):919-927.

[6] 赵燕江,张永德,姜金刚,邵俊鹏.基于Matlab的机器人工作空间求解方法[J].机械科学与技术,2009,12:1657-1661.

[8] 张新敏,朱学军,赵晨晨,陈官.基于MATLAB的HP20机器人运动学分析与仿真[J].制造业自动化,2014,(13):12-15.

[9] 李鹏,张凡凡,杨文权,韩恒恒,赵进.仿人机器人抬起重物的运动学仿真[J].制造业自动化,2015,(5):38-41.

[10] 刘萍,陈莹.自由度关节式机械手运动学分析及仿真[J].制造业自动化,2011,33(19):9-11.

作者简介：冯浩（1970 -），男，江西景德镇人，教授，博士，研究方向为智能机电系统设计相关理论和应用。

基金项目：国家自然科学基金项目：施釉机器人在陶瓷坯体自由曲面作业的关键技术研究（51165011）；江西省自然科学基金：复杂异形陶瓷的机器人施釉作业关键技术研究（2010GZC0090）；江西省科技支撑计划项目：机器人施釉技术的研发（20122BBE500039）；江西省高等学校科技落地计划资助项目：机器人喷釉系统的开发

收稿日期：2015-11-13

中图分类号：TP241

文献标识码：A

文章编号：1009-0134(2016)03-0020-05