基于Hilbert-Huang变换的制动意图聚类识别

唐先智，王 波，杨树军，马 雷

(燕山大学车辆与能源学院，秦皇岛 066004)

2016094

基于Hilbert-Huang变换的制动意图聚类识别

唐先智，王 波，杨树军，马 雷

(燕山大学车辆与能源学院，秦皇岛 066004)

为了进一步提高电动汽车再生制动系统对驾驶员制动意图的识别准确率，从而使电动汽车能在制动的过程中回收更多的能量，提出了基于Hilbert-Huang变换(HHT)的电动汽车制动意图聚类识别方法。建立了HHT的数学模型，基于HHT在时频域中进一步探寻中等制动和平缓制动两种制动意图下制动踏板行程信号的特征。建立了制动踏板行程信号特征提取模型，运用Hilbert局部边际能量谱得到局部特征能量，从而对信号特征进行提取，获取信号的特征向量。建立基于模糊C均值聚类算法的制动意图识别模型，并分别进行了离线实验和实时实验。结果表明所提出的基于HHT的制动意图模糊C均值聚类识别方法能更好地分辨中等制动和平缓制动意图，提高了识别准确率，并具有较好的实时性。

电动汽车；制动意图；Hilbert-Huang变换；聚类识别

前言

电动汽车制动控制策略对再生制动和机械制动在制动过程中使用比例的分配依据是驾驶员的制动意图[1-2]。驾驶员制动意图识别准确与否直接影响到电动汽车再生制动的能量回收率。因此，如何能够准确地识别驾驶员制动意图是电动汽车再生制动技术需要解决的重要问题[3-4]。国外制动意图识别技术主要应用在电动汽车再生制动系统和制动辅助系统上，研究开展较早，很多汽车企业已经把制动意图识别技术应用到量产车型中。但是，国外各大汽车企业都没有公开关于电动汽车制动意图识别的核心技术细节[5-9]。

国内学者针对电动汽车驾驶员在制动过程中的制动意图识别方法进行了相关研究。文献[10]中以制动踏板角速度、车速方差和车辆减速度作为制动意图识别的参数，利用模糊逻辑对驾驶员制动意图进行辨识。文献[11]中确定了以制动踏板角速度识别制动意图，以制动管路压力表征目标制动强度。采用模糊辨识算法进行制动意图识别。文献[12]和文献[13]中以制动踏板位移为制动意图识别的参数。文献[14]和文献[15]中以制动踏板位移及变化率并结合车速识别驾驶员的制动意图。文献[16]中以制动踏板行程及其变化率为识别参数，运用数理统计法制定识别参数的隶属函数和模糊推理规则并用神经网络对识别参数的隶属函数进行了优化，通过模糊算法可较准确地识别制动意图。由上述可见，国内制动意图识别主要是以制动踏板行程及其变化率等时域参量为识别参数，通过逻辑推断或模糊推理识别驾驶员的制动意图。这种识别方法平均识别准确率在90%左右，对于紧急制动和中等制动辩识率较高，在95%左右。但在辨识平缓制动和中等制动的过程中，驾驶员对制动踏板的操作特征不明显，若直接用制动踏板行程及其变化率等时域参数表征制动意图，则临界状态不易区分，易受到测量误差的干扰，识别准确率低于90%有时甚至低于80%。因此应对识别参数信号进行进一步挖掘，探寻识别参数更深层次的特征，提高识别分辨率。

于是，本文中提出了基于Hilbert Huang变换(Hilbert-Huang transform，HHT)的电动汽车制动意图识别方法。首先运用HHT对制动踏板行程信号在时频域内进行数据挖掘，得到制动踏板行程信号在时频域的特征，然后采用聚类识别算法对制动意图进行识别，从而进一步提高制动意图识别的分辨率和准确率。

1 Hilbert-Huang变换

对于制动踏板行程这样的非平稳数据信号，直接进行Hilbert变换得到的结果很大程度上失去了原有的物理意义。因此数据信号应首先进行经验模态分解(empirical mode decomposition, EMD),将数据信号分解为平稳的固有模态函数(intrinsic mode function, IMF)，即将信号经过经验模态分解(EMD)，使真实存在的不同尺度波动或趋势逐级分解开来，产生一系列具有不同特征尺度的数据序列，每个序列称为一个固有模态函数(IMF)。之后再进行Hilbert变换便能够得到能量在频率以及时间上的分布规律，从而表征信号的局部特征。

1.1 EMD原理与算法

IMF可以直接进行Hilbert变换得到能量在频率以及时间上的分布规律。而一般的信号往往是复杂的信号，并不满足IMF的定义。因此文献[17]和文献[18]中假设：任何复杂信号都是由许多简单的、不同的、非正弦的IMF分量(可以是线性的，也可以是非线性的)组成。根据此假设，提出了EMD算法(即Huang变换)，该算法有两个重要作用：一个是去除叠加模态，另一个是使波形更对称。这是HHT变换的关键环节。

首先找出初始信号X(t)上所有的极值点，然后分别对所有极大值点和极小值点进行三次样插差值，拟合出初始信号的上包络线Xmax(t)和下包络线Xmin(t)。取上下包络线的均值m1(t)：

m1(t)=[Xmax(t)+Xmin(t)]/2

(1)

用初始信号减去包络线均值得到h1(t)：

h1(t)=X(t)-m1(t)

(2)

如果h1(t)不满足IMF所需的条件，则将h1(t)作为初始信号，重复以上步骤得：

h11(t)=h1(t)-m11(t)

(3)

式中：m11(t)为h1(t)的上下包络线均值。若h11(t)仍不满足IMF的条件，则重复上述算法k次得：

h1k(t)=h1(k-1)(t)-m1k(t)

(4)

h1k(t)筛选过程终止判据为

(5)

式中SD为相邻两个处理结果的标准差。SD的取值不能过小也不能过大。SD过小会造成得到的IMF频率调制信号幅值恒定，失去信号特征；SD过大会使终止条件过于宽松，筛选结果无法满足IMF的条件。经验表明，要保证IMF既是线性的，又具有稳定性并且具有物理特征，SD应取0.2～0.3之间的数值比较合适。

如果式(4)中的h1k(t)符合终止判据的要求，则h1k(t)为1阶IMF，用c1(t)表示。用初始信号X(t)减去1阶IMF得到信号残差r1(t)：

r1(t)=X(t)-c1(t)

(6)

r1(t)可作为新信号再重复以上的EMD过程，经多次迭代可得所有信号残差ri(t)：

ri(t)=ri-1(t)-ci(t),i=2,3,…,n

(7)

当残差rn(t)成为单调函数时，即不可能再从中提取IMF分量时，便可终止EMD过程。可见，初始信号X(t)可由n阶IMF和残差rn(t)组成：

(8)

1.2 Hilbert变换与Hilbert谱

对式(8)中的每个IMFci(t)做Hilbert变换：

(9)

构造解析信号：

zi(t)=ci(t)+jH[ci(t)]=ai(t)ejΦi(T)

(10)

(11)

(12)

式中：ai(t)为幅值函数；Φi(t)为相位函数。

根据式(12)可求得瞬时频率：

(13)

初始信号可表示为

(14)

式中Re表示取实部。

根据式(14)可定义Hilbert谱的表达式：

(15)

式中Hilbert谱H(ω,t)描述了信号幅值随时间和频率的变化关系。

1.3 制动踏板行程信号的Hilbert-Huang变换

将制动踏板行程的数据信号输入计算机，运用MATLAB软件在计算机中编写Hilbert-Huang变换的程序。EMD算法(即Huang变换)程序流程如图1所示。Hilbert变换的流程如图2所示。

图3和图4分别为中等制动和平缓制动时制动踏板行程信号的实验数据。平缓制动时制动减速度小于1.6m/s2，制动踏板行程一般小于全行程的30%，这种制动的制动强度小，制动紧急程度也很小。对于电动汽车，在这种制动工况下要尽量使用再生制动，回收尽可能多的制动能量。中等制动时制动减速度介于1.6～3m/s2，制动踏板一般介于30%～60%，制动踏板行程变化率一般介于每秒65%～140%，这种制动的制动强度中等，制动紧急程度也为中等。电动汽车在这种制动工况下要适当加大机械制动的比例，确保制动的安全性。各截取如图3和图4狭长椭圆圈内所示的两组实验数据的一段进行Hilbert-Huang变换。所截取的实验数据如图5和图6所示。分别对截取的两段实验数据运用EMD算法进行Huang变换，分解得到的初始数据信号的固有模态函数(即IMF分量)如图7和图8所示。分别对中等制动和平缓制动数据信号的IMF分量进行Hilbert变换，得到两段数据信号的Hilbert谱，如图9和图10所示。从图9和图10可以看出，中等制动时与平缓制动时的制动踏板行程信号的幅值在频率和时间上的分布特征有明显不同。通过适当算法进行特征提取，便可对两种制动模式进行辨识。

2 特征提取与聚类识别

从前面的分析可以看出，通过对不同制动意图下制动踏板行程信号的Hilbert-Huang变换，进一步挖掘了该信号的时频域特征。下面从信号能量的角度，对中等制动和平缓制动时制动踏板行程信号的特征进行提取，并运用模糊C均值聚类算法对这两种制动意图进行识别。

2.1 特征提取

由于制动踏板行程信号为电压信号，因此可以把制动踏板行程信号的平方值当作信号的能量。对它进行Hilbert-Huang变换，便得到Hilbert能量谱，记为H2(ω,t)。根据能量守恒定律，Hilbert-Huang变换前后制动踏板行程信号能量守恒，如式(16)所示。使H2(ω,t)对时间进行积分，可得制动踏板信号的Hilbert边际能量谱，它表达了每个频率在整个时间长度内能量的累积，描述了累积的能量随频率分布的情况，如式(17)所示。同理，求出制动踏板行程信号的每个IMF分量的Hilbert能量谱Hi2(ω,t)，使Hi2(ω,t)对时间进行积分，可得到每个IMF分量的Hilbert边际能量谱，即制动踏板信号的Hilbert局部边际能量谱Ei(ω)，如式(18)所示。使Ei(ω)对频率进行积分，得到局部特征能量，如式(19)所示。由此可得制动踏板行程信号的特征向量，如式(20)所示。特征向量的每个元素为每个IMF分量的局部特征能量与总特征能量的比值。

(16)

(17)

(18)

(19)

T=[E1/E,E2/E,…,En/E]

(20)

2.2 制动意图识别

模糊C均值聚类算法的核心思想是找到样本的聚类中心，使样本到聚类中心的加权距离平方和最小。该算法的目标函数为

(21)

式中：μij为第j个样本隶属于第i类制动意图的程度；dij为样本点xj到第i类制动意图聚类中心的欧式距离，即dij(xj,zi)=‖xj-zi‖；Z为聚类中心，即Z=(z1,z2,…，zc)；m为加权指数；C为制动意图的分类数，表示将样本集{x1,x2,…,xn}分为C类制动意图；U为初始隶属度矩阵。

模糊C均值聚类算法的迭代方程如式(22)和式(23)所示，迭代终止条件如式(24)所示。

(22)

(23)

‖Z(p)-Z(p+1)‖<ε

(24)

式中：C为制动意图分类数，2≤C≤n，n为样本个数；ε为迭代停止阈值；Z(0)为初始聚类中心；Z(p)为第p次迭代的聚类中心，p为迭代次数；m为加权指数。

3 实验验证

3.1 离线验证

选取中等制动和平缓制动的制动踏板行程信号样本，均取各自的前3阶IMF分量构造特征向量。以50个标准样本特征向量中每个元素的均值为初始聚类中心，如表1所示。加权指数m取2，聚类算法迭代终止阈值为10-6。

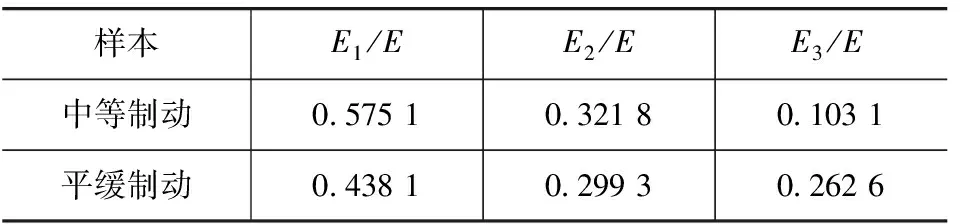
表1 样本的初始聚类中心

中等制动和平缓制动各选择10组制动踏板行程信号作为检测样本，两种制动意图共计20个检测样本。检测样本1～10为中等制动，11～20为平缓制动。在MATLAB软件环境下，对基于HHT的制动意图模糊C均值聚类识别算法进行离线验证，识别结果如表2所示。表3为基于模糊推理的制动意图识别结果，识别方法见文献[16]。

表2 基于HHT的制动意图聚类识别算法识别结果

表3 制动意图模糊推理识别算法识别结果

从表2中可以看出，识别算法将制动踏板行程信号的检测样本分别归入了两类制动意图。表中样本编号下面标记横线的样本为识别错误的样本，样本13和样本5识别错误，识别准确率为90%。从表3中可以看出，采用相同的检测样本，样本1，5，6，13和14识别错误，识别准确率为75%。

模糊推理识别法识别参数模糊化后的隶属函数如图11和图12所示。模糊推理规则如表4所示。

表4 模糊推理规则

运用模糊推理法识别正确的检测样本，如样本11，12，15，16，17，18，19和20为平缓制动样本。制动踏板行程变化率相对于制动踏板行程信号的测量难度更大，容易对识别结果产生干扰。其中样本11，12，17，18和20的制动踏板行程为“小”，这样从模糊推理规则可以看出无论制动踏板变化率为“小”、“中”或“大”，识别结果都为平缓制动。制动踏板变化率信号不会对识别结果产生负面影响，因此这5个样本相对容易识别。样本15，16和19也为平缓制动，制动踏板行程为“中”，制动踏板行程变化率为“小”并且小于0.4，此时制动踏板行程变化率很小，信号稳定，易于测量并且此时制动踏板行程变化率隶属于“小”的隶属度为100%，因此对于这3个样本模糊识别方法也能够准确识别。

对于识别错误的样本1，5和6，其制动踏板行程为“中”，制动踏板行程变化率为“小”，识别结果为平缓制动，这与实际不符。从模糊推理规则可以看出，只有制动踏板行程为“中”时，推理的结果才有可能是中等制动。由于隶属函数与模糊推理规则是通过大量的数理统计并经过反复优化得到，相对稳定，因此导致识别结果错误的原因应是制动踏板行程变化率信号测量有误，经模糊化后为“小”，实际应为“中”。可见，为更好地区分平缓制动和中等制动而引入的识别参数制动踏板行程变化率，由于其测量难度相对较大，测量值会有误差，有时反而会影响模糊推理结果。样本2，3，4，7，8，9，10，13和14的识别结果可以同理分析。文献[16]中所做的后续研究工作在文献[19]中加入了另一个识别参数车速，但仍没有解决上述问题。

基于HHT的制动意图模糊C均值聚类识别算法的识别参数只有制动踏板行程一个参数，并且易于测量。排除了制动踏板行程变化率这一不易测量准确参数的干扰，并省去了制动踏板角速度传感器，节省了成本。把对制动强度和制动紧急程度的辨识引入频域范围，在时频域内进一步挖掘制动踏板行程信号的时频特征，运用Hilbert能量谱提取信号的特征向量并进行聚类识别。识别准确率提高了15%。

基于HHT的制动意图模糊C均值聚类识别方法中的EMD算法，容易受到信号中干扰成分的影响，会导致信号极值点的偏差，从而对极值点的包络拟合也产生偏差。尤其是信号有间断或脉冲时，容易产生模式混叠现象。因此在实际对信号进行EMD分解的过程中，同一频率的成分会被分到多个IMF中，也可能在一个IMF中包含多个分量的成分。从而使每个IMF局部特征能量改变，导致特征向量和初始聚类中心的偏移，使某些识别结果产生偏差。如表2所示，基于HHT的制动意图聚类识别算法识别结果中仍有两个样本5和13识别错误。今后的工作是进一步提高EMD算法的抗干扰能力，进一步提高制动意图的识别准确率。

3.2 实时验证

实时验证采用的实验用车为解放牌混合动力公交车，其型号为CA6120URH1。制动踏板行程信号的在线采集、数据处理和制动意图的在线识别则选用与MATLAB软件兼容的通用控制器dSPACE/MicroAutoBox1401/1504。由于CA6120URH1车的CAN总线上，制动踏板行程为开关量，即其数值为0或1，不能直接用来进行制动意图识别，因此须自制制动踏板行程传感器对制动踏板行程信号进行采集，并输入到MicroAutoBox中进行在线数据处理和制动意图在线识别。在线识别之前须通过程序下载接口将基于HHT的制动意图模糊C均值聚类识别算法的程序代码下载到MicroAutoBox中。制动踏板行程实时信号如图13所示，它是通过驾驶员按要求(即一次中等制动，一次平缓制动)对制动踏板进行操作并在线采集得到的。图13中标记了制动踏板行程实时信号与其相应的制动意图。制动意图的在线识别结果如图14所示，可见该算法可以准确地在线识别驾驶员的制动意图。图15示出制动意图在线识别响应时间，可以看出，从进入制动模式到识别出第一个中等制动意图，在线识别时间为0.4s，符合中等制动意图与平缓制动意图识别的响应速度要求。

4 结论

(1)基于HHT的制动意图模糊C均值聚类识别算法可在时频域内对制动踏板行程信号的特征进行进一步的挖掘，提取其信号的特征向量，能对中等制动和平缓制动进行准确地辨识。离线实验证明，本算法相比于单纯在时域内的模糊推理算法，减少了识别参数，减小了参数测量误差对识别结果的影响，识别准确率提高了15%，进一步提高了对中等制动和平缓制动意图的分辨能力。

(2)基于HHT的制动意图模糊C均值聚类识别算法具有较好的实时性。实时实验证明，本算法可实时对制动意图进行准确的在线识别，为制动意图识别技术在电动汽车再生制动领域中更好的实时应用奠定理论基础。

[1] 初亮, 王彦波, 姚亮,等. 制动能量回收系统的制动力矩协调控制仿真[J]. 华南理工大学学报(自然科学版), 2014, 42(4):137-142.

[2] HAN J, PARK Y, PARK Y. Cooperative Regenerative Braking Control for Front-wheel-drive Hybrid Electric Vehicle Based on Adaptive Regenerative Brake Torque Optimization Using Under-steer Index[J]. International Journal of Automotive Technology, 2014, 15(6):989-1000.

[3] 赵轩, 马建, 汪贵平. 基于制动驾驶意图辨识的纯电动客车复合制动控制策略[J]. 交通运输工程学报, 2014(4):64-75.

[4] 王玉海, 宋健, 李兴坤. 驾驶员意图与行驶环境的统一识别及实时算法[J]. 机械工程学报, 2006, 42(4):206-212.

[5] WASEKURA M, WANG C, LORENZ R D. A Transient Core Loss Analysis of Multiple-gap Inductor Designed for the 2010 Prius[C].Energy Conversion Congress and Exposition (ECCE), 2014 IEEE:2177 - 2181.

[6] MILLER F P, VANDOME A F, Mcbrewster J. Honda EV Plus[M].Alphascript Publishing, 2010.

[7] HIROSE T, TANIGUCHI T, HATANO T, et al. A Study on the Effect of Brake Assist Systems (BAS)[J]. SAE International Journal of Passenger Cars: Mechanical Systems, 2009(1):729-735.

[8] SCHICK B, BÜTTNER R, BALTRUSCHAT K, et al. Evaluation Methods for the Function and Quality of Driver Assistance Systems with Active Brake Control[J]. ATZ Worldwide, 2007, 109(5):14-18.

[9] Bernhard Eichhorn M, Steffen König, Thorsten Ullrich. Electronic Brake Control for Greater Active Safety[J]. ATZ worldwide, 2014, 116(9):50-53.

[10] 孙逸神. 基于模糊逻辑的制动意图离线识别方法研究[J]. 北京汽车, 2009(6): 21-23.

[11] 张元才, 余卓平, 徐乐,等. 基于制动意图的电动汽车复合制动系统制动力分配策略研究[J]. 汽车工程, 2009, 31(3):244-249.

[12] 王英范,宁国宝,余卓平.乘用车驾驶员制动意图识别参数的选择[J].汽车工程, 2011,33(3): 213-216.

[13] 李玉芳,吴炎花.电-液复合制动电动汽车制动感觉一致性及实现方法[J].中国机械工程, 2012,23(4):488-492.

[14] 林逸,沈沉,王军,等.汽车线控制动技术及发展[J]. 汽车技术, 2005(12):1-3.

[15] 马朝永,化北,王震,等.电子制动踏板感觉模拟器研究[J].电子测量技术, 2011,34(7):28-32.

[16] 王庆年,孙磊,唐先智,等. HEV 制动意图识别的研究[J].汽车工程, 2013,35(9): 769-774.

[17] HUANG N E, SHEN Z, LONG S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 1998, 454:903-995.

[18] BATTISTA B, KNAPP C, MCGEE T, et al. Application of the Empirical Mode Decomposition and Hilbert-Huang Transform to Seismic Reflection Data[J]. Geophysics, 2007, 72(2):H29-H37.

[19] 王庆年, 王俊, 陈慧勇,等. 混合动力车辆中的加速与制动意图识别[J]. 吉林大学学报(工学版), 2014, 44(2):281-286.

Cluster Identification of Braking Intention Based on Hilbert-Huang Transform

Tang Xianzhi, Wang Bo, Yang Shujun & Ma Lei

CollegeofVehiclesandEnergy,YanshanUniversity,Qinhuangdao066004

For further enhancing identification accuracy rate on the braking intention of driver so as to make electric vehicle recover more energy, a cluster identification method of braking intention for electric vehicles is proposed based on Hilbert-Huang transform (HHT). A mathematical model for HHT is built, and based on HHT the brake pedal signal features under both moderate and gentle braking intentions are further explored in time/frequency domains. An extraction model for brake pedal travel signal feature is set up, Hilbert marginal energy spectrum is used to acquire local feature energy, and hence the signal features are extracted with corresponding eigenvectors obtained. Then the braking intention identification model is established based on fuzzy C-means clustering algorithm, and both offline and real-time experiments are performed respectively. The results show that the identification method proposed can better distinguish moderate and gentle braking intentions, raise identification rate with better real-time performance.

electric vehicles; braking intention; Hilbert-Huang transform; cluster identification

*国家自然科学基金青年基金(51505414)、河北省高等学校科学研究项目(Z2015081)和燕山大学博士基金(B794)资助。

原稿收到日期为2015年12月24日，修改稿收到日期为2016年3月3日。