一个新的超混沌耦合发电机系统及其超混沌控制

谢艳云，蔡文良

(重庆水利电力职业技术学院， 重庆　永川　402160)



一个新的超混沌耦合发电机系统及其超混沌控制

谢艳云，蔡文良

(重庆水利电力职业技术学院， 重庆永川402160)

[摘要]在三维耦合发电机系统的基础上,引入非线性控制器，构建一个新的超混沌耦合发电机系统，分析了新系统平衡点的性质、Lyapunov指数谱、吸引子的相图等动力学特性；利用线性反馈控制法，通过设计合适的反馈增益,实现了新系统的超混沌控制.理论分析和数值仿真验证了该方法的有效性.

[关键词]分数阶系统；延迟；混沌； 同步

近年来,混沌已经成为非线性科学研究领域的热点问题,混沌系统在通信、电路、经济、生物和化学等领域得到了广泛应用[1].混沌系统的复杂动力学行为特性为保密通信和图像加密提供了新思路,但用简单的混沌系统加密信息并不安全.1979年，Rossler首次给出了超混沌概念,并提出了超混沌系统[2].超混沌系统具有两个或两个以上的正Lyapunov指数,其相轨迹较一般混沌吸引子而言,具有更为复杂的动力学行为,系统的动态行为更难预测,具有更大的密钥空间.本文在前人的研究基础之上,基于耦合发电机系统[3]引入一个非线性控制器,构造一个新的超混沌耦合发电机系统,分析了系统的耗散性、Lyapunov指数与Lyapunov维数和吸引子等动力学行为.根据Routh-Hurwitz判据设计线性反馈控制器,对系统进行超混沌控制.数值模拟结果证实了该方法的有效性.

1新四维超混沌系统模型

根据文献[3]和[4],三维耦合发电机系统的状态方程表示为

(1)

当参数μ=2,a=3,ε=1时,三维耦合发电机系统处于混沌状态,混沌吸引子如图1所示.

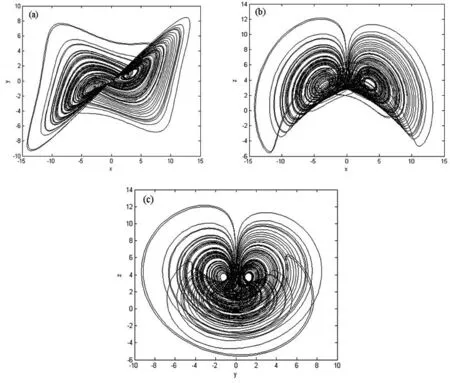
(a)x-y平面 (b)x-z平面 (c)x-w平面图1　系统(1)的混沌吸引子

根据产生超混沌吸引子的条件[5，6]，基于系统(1)的第一个方程引入一个非线性控制器w,其中m为新引入的参数，构成一个新的四维超混沌耦合发电机系统.该系统的状态方程表示为

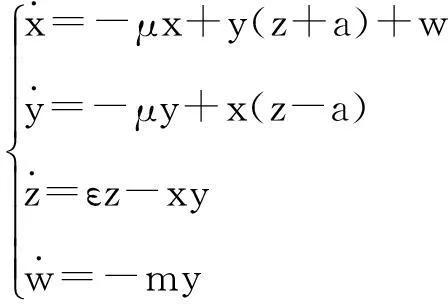
(2)

新系统(2)保证了系统的维数为4,并且含有非线性乘积项,满足了产生超混沌的必要条件.

2新超混沌系统的动力学分析

2.1耗散性

对于新系统(2),向量场的散度:

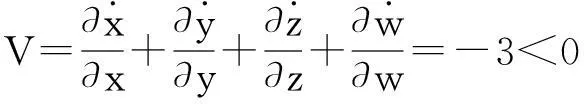
可见，新系统(2)是耗散的,并以指数形式e-3收敛.当t→∞时,包含系统轨线的每个小体积元以指数速率-3收缩到0.这说明系统的所有轨迹最终会被限制在一个体积为零的极限子集上,系统的动力学行为最终趋向于一个吸引子,说明吸引子的存在性.

2.2Lyapunov指数与Lyapunov维数

从系统的吸引子相图和时间响应图上很难区分混沌系统和超混沌系统.Lyapunov指数是定量描述轨线彼此排斥和吸引的量,通过Lyapunov指数谱图[7]可以十分清楚地区分系统所处的各个状态.一个四维连续自治系统的4个Lyapunov指数中,有2个大于0、1个等于0、1个小于0时系统处于超混沌状态;1个大于0、1个等于0、2个小于0时系统处于混沌状态;2个等于0、2个小于0时系统处于准周期状态;1个等于0、3个小于0时系统处于周期态.

当固定参数μ=2,a=3,ε=1时,变量x随参数m在[0,30]变化的Lyapunov谱图如图2(a)所示.图2(b)为图2(a)中m在[0,3]变化的放大图.由图2可以十分清楚地看到新系统(2)随参数m变化的运动情况.

当固定参数μ=2,a=3,ε=1,m=1.5时，利用Wolf方法[8]计算该四维非线性系统的Lyapunov指数为λ1=0.164 9,λ2=0.089 1,λ3=0,λ4=-3.193 1 ,其中有2个大于0、1个等于0、1个小于0,说明新系统(2)在这组参数下处于超混沌运动状态.

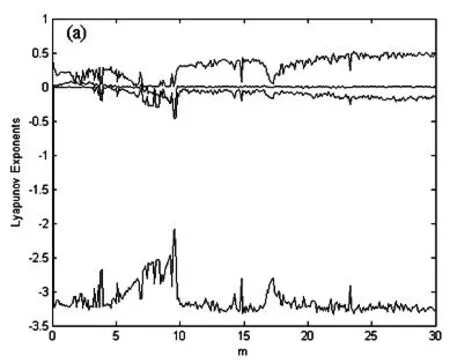
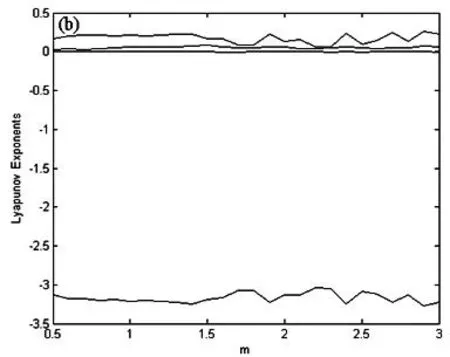
(a)m在[0,30]变化; (b)m在[0,3]变化图2　系统(2)的Lyapunov指数谱图

根据Kaplan-Yorke猜想公式,计算新系统(2)的Lyapunov维数为：

新系统(2)的维数是分数维数,进一步说明该系统在这组参数下处于超混沌状态.

在上述参数下,新系统(2)对应超混沌吸引子在各个平面上的投影如图3所示.由图3可知，新系统(2)的超混沌吸引子具有复杂的折叠和拉伸轨迹,说明超混沌系统比混沌系统具有更强的不稳定性.

2.3平衡点及其稳定性

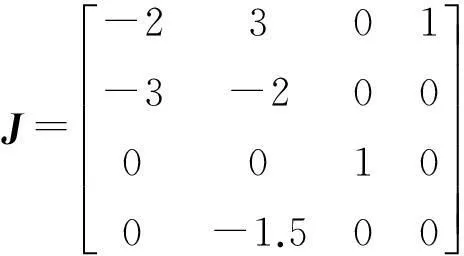
计算得到4个特征根分别是1, 0.313 5,-2.156 8+3.114 6i,-2.156 8-3.114 6i.其中有两个正值保证平衡点在某方向有排斥性,使其轨线分散.这从理论上证明了新系统(2)存在超混沌的可能性.

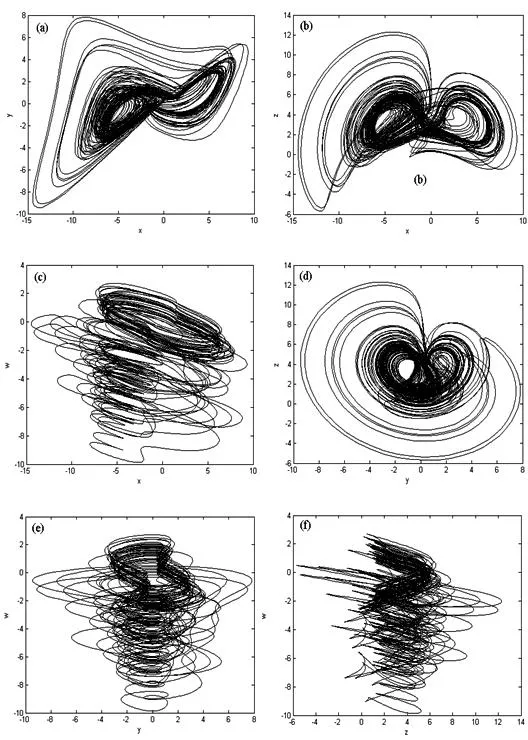
(a) x-y平面; (b) x-z平面; (c) x-w平面;(d) y-z平面; (e) y-w平面; (f) z-w平面图3　系统(2)的超混沌吸引子在各平面上的投影

3超混沌系统的线性状态反馈控制

采用线性状态反馈控制法[9],将新的超混沌耦合发电机系统(2)的超混沌运动控制到平衡点(0,0,0,0),构造如下的受控系统:

(3)

其中，k1x、k2y、k3z、k4w是线性反馈控制器,k1、k2、k3、k4是反馈系数.系统(3)在平衡点(0,0,0,0)处的Jacobia矩阵为

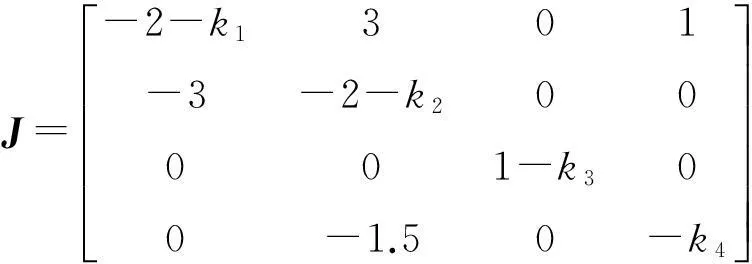
(4)

矩阵(4)的特征方程为：

(λ+k3-1)(λ3+b1λ2+b2λ+b3)=0

其中：

b1=4+k1+k2+k4

b2=13+2k1+2k2+4k4+k1k2+k1k4+k2k4

b3=13k4+2k1k4+2k2k4+k1k2k4

根据Routh-Hurwitz判据,当且仅当

k3-1>0,b1>0,b2>0,b1b2>b3

时Jacobia矩阵的所有特征值λ均具有负实部,因此只要k1、k2、k3、k4满足上式,受控系统(3)渐进稳定到平衡点(0,0,0,0).例如选取反馈系数k1=1,k2=1,k3=2,k4=1时,k1、k2、k3、k4满足Routh-Hurwitz判据,选取初始值为(1,2,3,4),步长为0.001.图4给出了受控系统(3)的时间序列图.数值仿真结果表明,新的四维超混沌耦合发电机系统(2)的4个状态变量x、y、z、w快速收敛到平衡点(0,0,0,0),说明采用线性状态反馈控制能有效地实现系统的超混沌控制.

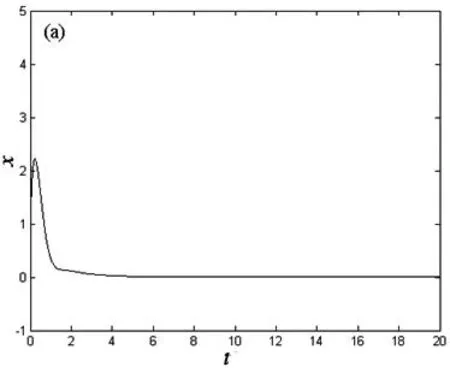
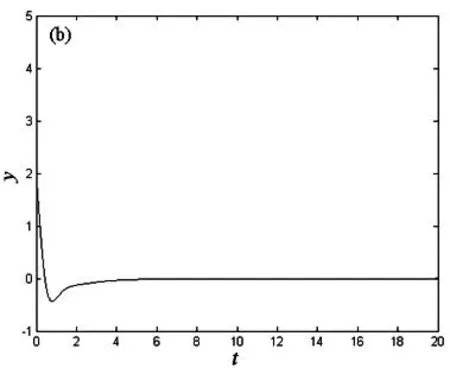
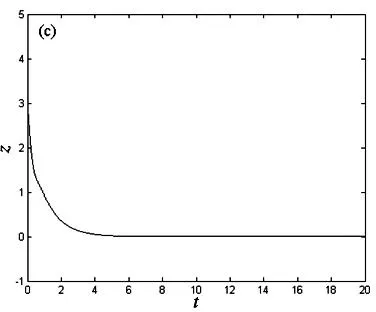
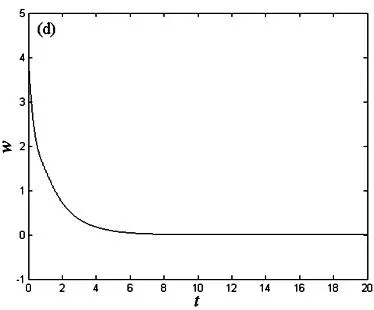
(a) t-x; (b) t-y; (c) t-z; (d) t-w图4　受控系统(3)的时间序列图

4结论

本文提出基于三维耦合发电机系统构造一个新的四维耦合发电机超混沌系统,通过理论分析和数值仿真,分析了新的四维耦合发电机超混沌系统的基本动力学行为，并基于线性反馈控制对该超混沌系统进行超混沌控制.根据Routh-Hurwitz判据，选择恰当的反馈增益,使新的四维耦合发电机超混沌系统的不稳定行为快速得到控制，而且代价小.所得结果说明：该超混沌系统具有一定的实际应用价值,值得进一步研究与推广.

[参考文献]

[1]CHEN G, DONG X. From chaos to order:Methdologies,perspectives and applications[M].Singapore: World Scientific,1998.

[2]ROSSLER O E.An equation for hyperchaos[J].Physics Ltters A,1979,71(2):155-157.

[3]LEIPNIK R B,NEWTON T A.Double strange attractors in rigid body motion with linear feedback control[J].Physics Ltters A,1981,86(2):63.

[4]王兴元,武相军.耦合发电机系统的自适应控制与同步[J].物理学报,2006,55(10):5077-5082.

[5]章秀君,吴志强,方正.超混沌系统的构造方法研究[J].计算机工程与应用,2014,50(2):92-98.

[6]吴淑花,容旭巍,屈双惠,等.超混沌耦合发电机系统的混沌同步及其电路实现[J].四川大学学报,2013,50(3):515-520.

[7]刘秉正,彭建华.非线性动力学[M].北京:高等教育出版社,2005.

[8]WOLF A,SWIFT J B,SWINNEY H L,et al.Determining lyapunov exponents from a time series[J].Physics D:Nonlinear Phenomena,1985,16(3):285-317.

[9]李瑞红,徐伟,李爽.一类新混沌系统的线性状态反馈控制[J].物理学报,2013,30(3):65-68.

(责任编辑穆刚)

A new four dimensional hyperchaotic coupled dynamos system and its hyperchaotic control

XIE Yanyun, CAI Wenliang

(Chongqing Water Conservancy and Electric Power Vocational Technology College, Yongchuan Chongqing 402160, China)

Abstract：The four dimensional hyperchaotic coupled dynamos system is built by adding a nonlinear controller to the three dimensional coupled dynamos system. Firstly, a set of parameters are identified when the system has hyperchaotic attractors. Then, the complex dynamic characteristics of the new system are analyzed, such as the dissipativity, the lyapunov exponents and lyapunov dimension, the equilibrium point. Hyperchaotic attractors is confirmed in the new system. Finally, the hyperchaotic motion of the new system is suppressed by using method of linear state feedback control. Theory and numerical simulations show the effectiveness of the method.

Key words：hyperchaotic; coupled dynamos system; lyapunov exponents’ spectrum; linear state feedback control

[中图分类号]O322

[文献标志码]A

[文章编号]1673-8004(2016)02-0019-04

[作者简介]谢艳云(1980—)，女，湖南娄底人,讲师，硕士，主要从事非线性系统理论方面的研究.

[基金项目]重庆水利电力职业技术学院院级资助项目(K201411).

[收稿日期]2015-10-26