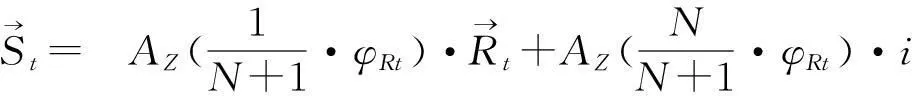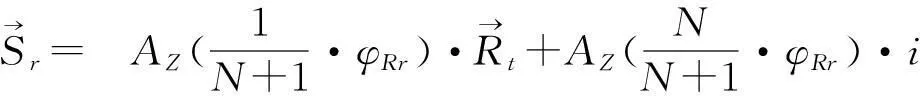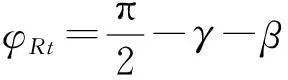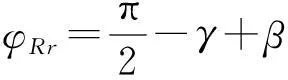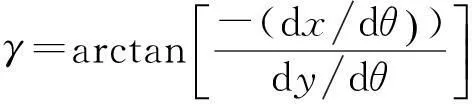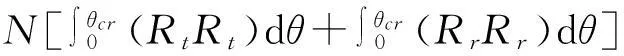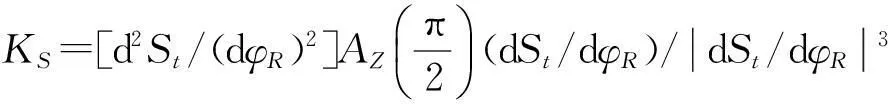螺杆钻具马达线型的优化设计

陈　欣， 赵　娜

(沈阳工业大学理学院， 辽宁　沈阳　110870)



螺杆钻具马达线型的优化设计

陈欣， 赵娜

(沈阳工业大学理学院， 辽宁沈阳110870)

[摘要]应用齿轮啮合理论原理，采用三次样条函数作为拟合曲线进行数值分析，得到离散的定子与转子共轭线型.以简单函数寻找解析解的方法为基础，扩散到以数值分析为基础寻找优化解的范围.将简单函数求解法与三次样条插值法进行比较，证明了优化方法的有效性与可行性.

[关键词]马达线型；优化；转子；定子；螺杆钻具

螺杆机械是以共轭螺旋曲面啮合为工作原理的一类高技术机械装备.单螺杆马达是一类应用非常广泛的单螺杆动力装置.它将液体(泥浆)的势能转换成转子的动能，实现对钻具转子钻头的驱动.定子和转子是螺旋机械的重要零件，线型是指单螺杆马达的转子和定子在横截面中的曲线形状.螺杆端面线型对钻具的性能影响较大，因此端面线型的设计需遵循严格的要求：密封性能佳、传动性能优、工艺性能好.

目前，在国际上排在前三名的单螺杆钻具生产制造企业是美国斯伦贝谢公司、美国贝克休斯公司和美国哈里伯顿公司.在单螺杆机械设计制造方面，这些公司的定转子线型设计一直沿用1939年法国人莫诺提出的用数学解析方程式表示的共轭曲线作为定转子廓形的传动设计理论.

从定转子的线型优化设计到螺旋曲面的成型理论及制造工艺方法，国内外学者都做了大量的理论和应用研究，但在单螺杆机械内螺旋定子截面廓形检测方面国内外没有相关报道.近期，沈阳工业大学国家科技园在单螺杆动力装置优化设计方面通过对注胶后的内螺旋定子进行检测，根据检测结果重新设计出新的转子线型，这样加工出的转子和注胶后的定子就能达到理想的啮合，大幅度提高了螺杆副的啮合精度.

本研究主要是在数控加工技术可以满足任意三维离散表面和二维曲线的成型要求，以及计算机辅助技术解决了复杂共轭啮合方程及超越函数数值求解[1]的基础上，应用啮合理论建立螺杆钻具马达线型方程，选用三次样条函数作为拟合曲线，以数值分析为基础求离散的数值优化解的范围，最终实现螺杆钻具马达线型的优化设计.

1螺杆钻具马达线型的理论基础

1.1啮合理论基础

单螺杆马达是螺杆钻具的主要动力部件，马达总成是由转子和定子两个基本部分组成的容积式动力机械.然而，转子和定子能够形成一个容积式马达应具备以下基本条件[2]：

(1)密封条件：定转子曲面应组成空间共轭封闭，即转子、定子副必须大于马达的最小长度，并具有合适的间隙值；

(2)连续下移条件：转子连续转动能导致密封腔沿轴向向下连续移动；

(3)隔离条件：转子、定子副能形成相互分隔的密封腔，即：转子在定子的任何位置时过流截面能分成确定的互不连通区域；

(4)消失条件：当转子在定子中运动时，各个区域的大小能从最大变为零.

转子、定子副在工作时，定子固定不动，而螺杆马达螺旋转子在定子内作偏心距为e的平面行星运动，定子曲面就是在这种确定的相对运动条件下转子螺杆曲面的包络曲面.

在平面行星运动中，假设转子为5头螺杆，定子为6头螺杆，转子与定子中心距为偏心距e，让定子保持不动，转子在绕自身回转中心作顺时针方向自转运动的同时，又绕定子衬套中心作方向为逆时针的公转运动.运动过程中，转子与定子在任何位置都有若干个啮合点，每个啮合点的位置连续变化，所形成的啮合线是一条连续曲线.于是，转子和定子能够啮合的条件为：

(1)转子与定子的头数比为N/(N+1)；

(2)转子与定子具有相同的偏心距e；

(3)转子与定子的导程比为N/(N+1)；

(4)转子与定子的啮合线连续.

1.2三次样条曲线

在实际生产中，端截面廓形往往不能用解析方程式的形式给出，而是通过设计、测量、实验得到离散点坐标(xi，yi)(i=0,1，…，n)进行描述.可先将离散数据点进行曲线拟合，构成端面的近似截面曲线，再形成空间螺旋面.将曲线拟合成连续曲线的方法有很多种，但由于有些实际问题要求二阶导数连续，且在节点处只给出函数值，不给出导数值，同时保证曲线光滑性较好，因此，插值方法的选取主要考虑三次样条函数[3，4].

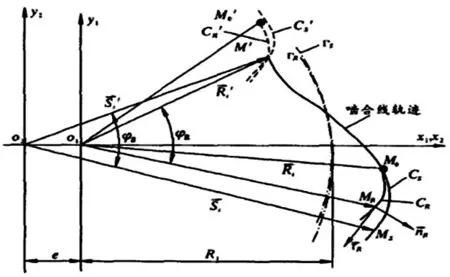
设[a，b]上有插值节点a≤x0

(i)S(x)∈C2[a，b](C2[a，b]代表[a，b]上二阶导数连续的函数集合)；

(ii)S(xi)=yi(i=0,1，…，n)；

(iii)S(x)在每个小区间[xi，xi+1](i=0，1，…，n-1)上是三次多项式；

则称S(x)为三次样条插值函数.在采用三次样条拟合螺旋曲面廓形时，需保证拟合段内曲线的横坐标x保持单调性.如果被拟合曲线的横坐标x不单调，可采用分段拟合法对每个小区间进行分段处理.

由上述定义可知，S(x)在每个小区间[xi，xi+1](i=0，1，…，n-1)内为一个三次多项式，需确定4个待定系数；共有n个小区间，故需要确定4n个系数.根据S(x)∈C2[a，b]，在节点xi(i=0,1,…,n)处应满足连续性条件：

S(xi-0)=S(xi+0)

S′(xi-0)=S′(xi+0)(i=0，1，…，n-1)

S″(xi-0)=S″(xi+0)

共有3n-3个条件，再加上S(x)满足插值条件S(xi)=yi(i=0，1，…，n)，总共有4n-2个条件.要想唯一确定S(x)还必须附加两个条件.通常在[a，b]的两端点a=x0，b=xn给出约束条件(称为边界条件)[5，6].因为螺杆转子各段齿形间是圆弧连接，所以本文采用的边界条件为：

(1)

2螺杆钻具马达共轭线型的优化设计模型

2.1螺杆钻具马达的共轭线型模型

如图1所示，设转子的齿顶曲线CR是已知的光滑连续函数，CS是与其共轭的定子曲线，M0是两曲线在初始位置的啮合点；φR、φS为独立运动参数；转子和定子自初始位置分别转过φR、φS后曲线CR和CS到达CR′和CS′的位置.此时，两曲线上必有某接触点M′是转子齿廓与定子齿廓的公共点.

图1　定子与转子的共轭啮合运动

由齿轮啮合原理，螺杆钻具马达转子与定子齿廓的共轭啮合方程[7，8]为：

(2)

定子共轭线型的通用方程[9，10]为:

θ∈[-θcr，θcr]

(3)

θ∈[-θcr,θcr]

(4)

其中：

γ是转子齿顶曲线CR上任意点的切线矢量τR与x1轴的夹角，e是定子与转子的偏心距.

p=xsinγ-ycosγ.

2.2 螺杆钻具马达线型的优化设计

在螺杆马达中，描述共轭副的基本特征的参数主要是综合曲率、过流面积和相对滑动率三项.本文以最大综合曲率、最大相对滑动率和过流面积最大为目标函数，以无曲率干涉、具备足够的齿形接触强度和共轭线型的光滑连续性为约束条件来建立优化模型.

2.2.1目标函数

minF(X)=Wρmax(ρRS)+Wηmax(ηRS)+

WA(-ASR)

式中，

这里，Wρ、Wη和WA为权重系数，Wρ+Wη+WA=1；KR、KS分别为转子曲线CR和定子曲线CS的相对曲率.

ψ=[df(θ，φR)/dφR]+ζ[df(θ，φR)/dθ]，

ξ=-(i·H)/[i(dRt/dθ)].

2.2.2约束条件

(1)无曲率干涉

转子共轭曲线CR和定子共轭曲线CS在任意啮合点的诱导曲率[11-14]KRS为：

对于啮合的转子和定子，在啮合点的邻域内无曲率干涉的充要条件是：

KRS<0，

则其约束方程应为：

M1(X)=ψ<0.

(2)具备足够的齿形接触强度

为了保证转子和定子的共轭线型具有足够的耐磨性和抗疲劳强度，令

M2(X)=[(ρRt)min/ρRt]-1≤0，

M3(X)=[ρRt/(ρRt)max]-1≤0，

M4(X)=[(ρRr)min/ρRr]-1≤0，

M5(X)=[ρRr/(ρRr)max]-1≤0，

M6(X)=[(ρSt)min/ρSt]-1≤0，

M7(X)=[ρSt/(ρSt)max]-1≤0，

M8(X)=[(ρSr)min/ρSr]-1≤0.

其中，ρRt、ρRr、ρSt、ρSr分别是转子齿顶、转子齿根、定子齿顶、定子齿根的曲率半径.

(3)共轭线型的光滑连续性

转子齿顶Rt(θ)是预先给定的光滑连续曲线，虽然它满足数学理论，但未必在实际工程应用中适用，通常存在干涉现象，需要进行几何修形.为了满足齿形的密封和啮合原理，则在分界点需满足二阶导数连续的条件，即(1)式成立.

3实例分析

假设某螺杆钻具，转子与定子的头数比是5∶6，定子与转子的偏心距e=9 mm，其转子齿根的最小直径是(ΦRr)min=86 mm，定子齿顶的最大内径是(ΦSt)max=140 mm.应用优化模型及优化设计程序，对转子与定子的共轭线型进行计算研究.表1的3种线型方案分别是：普通内摆线外等距曲线，普通渐开线曲线，三次样条离散曲线.

表1　线型优化设计结果的比较(令WH=Wη=WA=1/3)

比较表1中的各项数据，可得到如下结论：

(1)表1中的数据表明，对于几何参数相同的螺杆马达，本文采用的三次样条离散曲线方法求得的转子与定子的共轭线型的最大综合曲率和最大相对滑动率指标均最小，即啮合性能最佳.同时，其共轭线型的过流面积也比普通简单函数的线型要大，可满足低转速大扭矩螺杆钻具马达的技术性能条件.

(2)选用普通内摆线外等距曲线、普通渐开线曲线这样的简单函数作为转子齿顶廓形的生成线，都存在不同程度的打扣和曲率干涉现象，很难得到定子与转子的共轭线型，实际应用中需要进行修正.详细研究发现，干涉点均出现在分界点处，因为这两种线型在分界点处的一阶和二阶导数不光滑连续.

由此可以推论：若利用三次样条离散曲线的方法，采用分段连续的转子廓形，螺杆钻具马达将会获得啮合性能较佳和过流面积较大的定子与转子共轭线型.

4结语

(1)本文运用啮合原理，建立螺杆钻具马达共轭线型通用方程组，构造的优化设计数学模型对内啮合传动副具有普遍的适用性.

(2)本文采用优化设计方法，将采用三次样条函数作为原始廓形曲线，所求得离散的定子与转子共轭曲线和普通摆线类与渐开线类曲线相比，线型光滑连续，无干涉现象发生，啮合性能指标好，过流面积大，最大综合曲率和最大相对滑动率小，是一种很有前景的线型方案.

(3)本文以数值分析为基础，寻找离散数据点的数值优化解的范围，区别于传统螺杆钻具马达定子与转子的共轭线型的优化，为优化设计提供了新的思路和方法.

[参考文献]

[1]万邦烈.单螺杆式水力机械[M].东营：石油大学出版社，1993:111-127.

[2]易先忠,高德利,何俊松，等.螺杆马达定转子共轭线形的优化设计模型研究[J].石油矿场机械，2004,33(2):1-4.

[3]封其军,曾励.螺杆泵转子的端面型线计算与加工仿真[J].农业装备技术，2010,36(2):41-44.

[4]程光仁,施祖康,张超鹏.滚珠螺旋传动设计基础[M].北京：机械工业出版社,1987：29-31.

[5]LIWQ,LIY,SUNWL.Researchandrealizationofcomplicatedscatteredpointsreconstructionmeans[J].MachineryDesign&Manufacture, 2007(7):45-48.

[6]王金铭,陈欣,刘艳秋.数值分析[M].大连：大连理工大学出版社,2008.

[7]谢竹庄.单螺杆马达的普通线型[J].石油学报,1997,18(2):98-103.

[8]王忠杰,易先中.单头单螺杆水力机械共轭线型分析[J].石油机械, 1997,25(7):1-4.

[9]易先中,高德利,何俊松，等.螺杆马达定转子共轭线形的优化设计模型研究[J].石油矿场机械，2004,33(2):1-4.

[10]易先中,高德利,何俊松,等.螺杆马达定子与转子共轭线型的研究[J].石油机械，2003(31):16-18.

[11]常高.共轭曲面的诱导曲率与润滑角[J].沈阳工业大学学报，1998,20(4):85-89.

[12]冯忆艰.克林贝格螺旋锥齿轮的诱导法曲率[J].淮南矿业学院学报，1995，16(2)：58-64.

[13]吴序堂.齿轮啮合原理[M].北京:机械工业出版社,1982.

[14]吴大仁.微分几何[M].北京:人民教育出版社,1959.

(责任编辑穆刚)

Research of optimum design method with positive displacement motor linear

CHEN Xin, ZHAO Na

(School of Science, Shenyang University of Technology, Shenyang Liaoning 110870, China)

Abstract：The application of theory of gear meshing principle, using cubic spline function fitting curves, to the numerical analysis, the discrete conjugate linear of stator and rotor is obtained. Based on the simple function for analytical solution method, spreading to the base of the numerical analysis the range of optimized solution is obtained. Compared with the simple function solving method and cubic spline interpolation method, the effectiveness and feasibility of the optimization method are verified.

Key words：motor linear; optimization; rotor; stator; positive displacement motor

[中图分类号]O29

[文献标志码]A

[文章编号]1673-8004(2016)02-0023-04

[作者简介]陈欣(1963—)，女，山东蓬莱人，教授，博士，主要从事工程数学、复杂曲面制造技术、曲面反求理论等方面的研究.

[收稿日期]2015-06-27