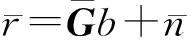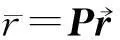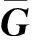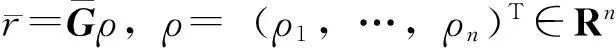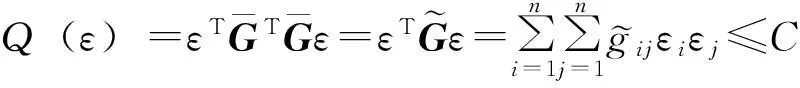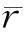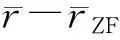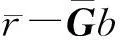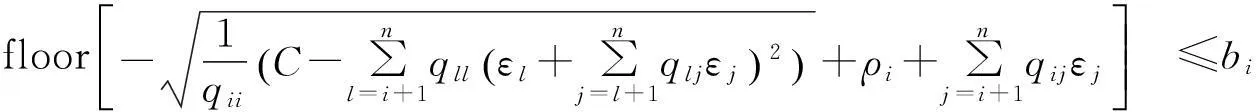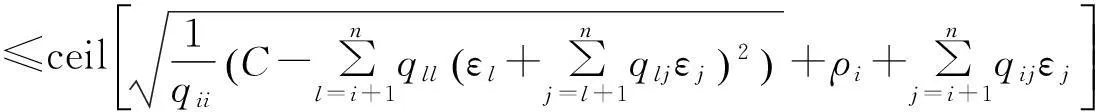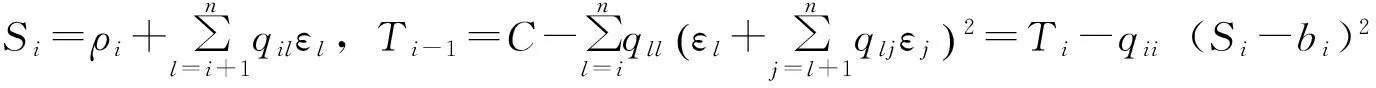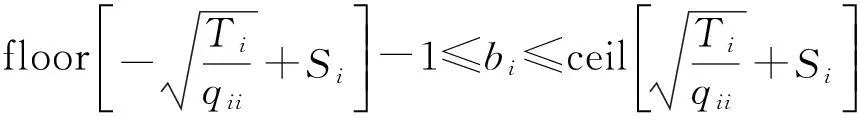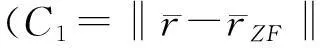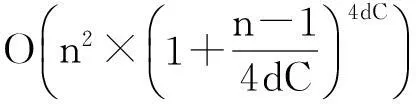一种基于MIMO系统的改进广义球解码算法
2016-04-11杨梅陈阳李满华安徽工程大学现代教育技术中心安徽芜湖241000
杨梅,陈阳,李满华 (安徽工程大学现代教育技术中心, 安徽 芜湖 241000)
一种基于MIMO系统的改进广义球解码算法
杨梅,陈阳,李满华(安徽工程大学现代教育技术中心, 安徽 芜湖 241000)
[摘要]基于球解码算法和广义球解码算法的思想,提出了一种基于MIMO系统的改进的广义球解码算法:引入一个置换矩阵,利用矩阵的正交性来简化运算;根据信噪比的特性来选择初始半径;根据Cholesky法分解格莱姆矩阵来进行格点搜索;通过求解格的二次型的最小值来确定范围的上下界。仿真结果表明,该算法有较强的抗多流干扰能力,在高信噪比的情况下性能有所改善,而且复杂度也相对较低。
[关键词]广义球解码算法;MIMO系统;复杂度
多输入多输出(Multiple-input Multiple-output,MIMO)系统采用多个收发天线,与传统的单输入单输出(Single-input Single-output,SISO)系统相比,MIMO系统在带来巨大信道容量的同时也产生极大的接收信号检测复杂度[1,2]。因此,基于信号和信道的统计特征,构建相应的检测算法以抑制多流干扰(Multi-Stream Interference,MSI)就成为提高系统性能的关键技术问题。为了解决最大似然算法[3]遍历式搜索的问题,Fincke和Pohst提出的球解码(Sphere Decoder,SD)算法[4]是将搜索的格点限制在一个合适的椭圆内,从纯数学的角度来研究最小二乘问题。Damen等[5,6]提出的广义球解码(Generalized Sphere Decoder,GSD)算法可以解决发送天线小于接收天线的非对称空时通信结构。基于球解码算法[4,7~9]和广义球解码算法[5,10,11]的思想,笔者提出一种改进的广义球解码算法。该算法由于引入一个置换矩阵可使算法变得更简单,根据信噪比的特性来选择合适的球面初始半径来缩小搜索格点的范围。该算法在高信噪比时复杂度较低。
1系统模型
考虑一个N×M的MIMO系统,该系统的发射天线数为N,接收天线数为M。将接收信号写成矢量形式为[2]:
r=Hx+n
(1)
式中,r=(r1,r2,…,rM)T是M×1维接收信号矢量;x=(x1,x2,…,xN)T是N×1维发射信号矢量;H为M×N的信道传输矩阵;n=(n1,n2,…,nM)T是M×1维加性高斯白噪声矢量;方差矩阵为2σ2IM(IM是M×M单位阵)。
最大似算法(Maximum Likelihood,ML)通过求解似然函数的最小值形成最佳信号矢量,其标准化形式为[2]:

(2)
ML算法是枚举搜索所有的待选码字,找出与接收信号r之间欧式距离最短的一个作为最优解,在N较大时,这是一个相当复杂的非多项式(Non-Polynomial,NP)问题,尽管误码率很小,但其计算复杂度在实际通信中是不能接受的。而球解码算法只考虑以接收信号向量为中心的球中的那些码字来限制可能的码字数,所以球解码算法的性能接近ML算法。
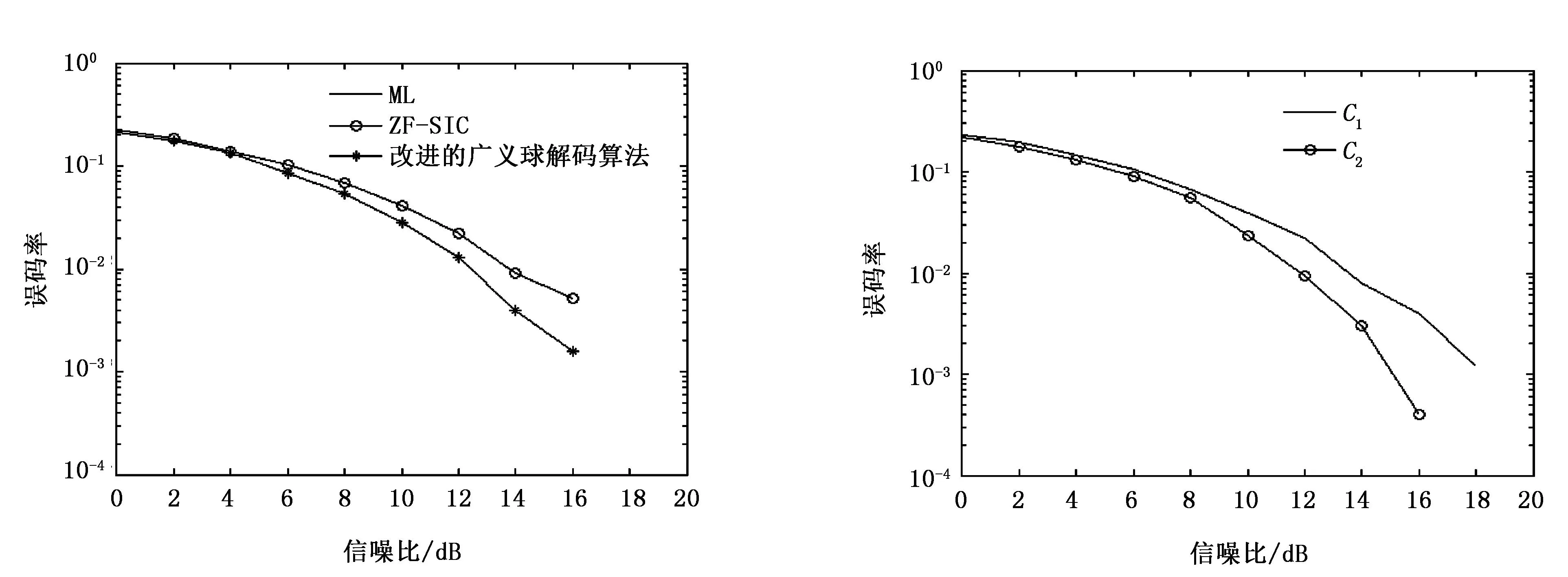
当N r′=MHu+n′ (3) 2改进的广义球解码算法 2.1引入置换矩阵P (4) 对式(4)两端同时左乘P(P为正交阵[15]),得到: (5) 2.2Cholesky法分解矩阵 (6) 该算法是把在接收信号空间的一个球内搜索发送信号映射点的问题转化为在发送信号空间中相应椭球体内搜索发送信号点的问题,从而最小化ε=ρ-b的问题可以转换为: (7) (8) 2.3初始半径的选择 (9) 算法的初始半径是根据接收信号所受信噪比的特性来选取的,接收信号与发射信号映射点的距离的平方服从卡尔方分布,即满足: (10) 式中,χ2(2N)表示自由度为2N(N为发送天线数)的卡尔方分布。 C=2ασ2N (11) 在仿真试验中,如果在以初始半径C的球内没有找到合理的点,则C按照1.2倍因子增大,即按照半径1.2C重新开始搜索。 2.4搜索最近格点 从式(8)的最后一个不等式往后递推,找出椭球体的上下界。这里首先要根据调制方式定义一个调制子集set(如4QAM,set=[-1,1],16QAM,set=[-3,-1,1,3])。首先考虑i=n项,对于任意bi(i=n,n-1,…,1)的一组可能的整数取值,根据这些固定的取值来得到bi的取值范围[6]: (12) (13) 式中,floor[a]表示取比a大的最小整数,ceil[a]表示取比a小的最大整数。 待确定上下界后,然后开始搜索。如果biset或者在该范围内没有合理的值,则相应的bi的取值应该丢弃。于是选择一组新的整数值,继续上面的搜索过程。如果bi∈set且有合理的取值,则选取一个合理的值,然后根据bi的取值,可以得到bi-1的取值范围。从i=n开始,依次计算i=n,n-1,…,1时bi的范围。 当找到球内的一个星座点时,计算该点距离球心的欧几里德距离的平方: (14) 3仿真结果和性能分析 假设一个平坦瑞利衰落中的MIMO系统,每对收发天线之间的信道衰落系数是相互统计独立的,噪声为高斯白噪声。假设信道衰落相对于信号传输速率来说变化缓慢,即能准确地估计信道的变化,且信道衰落在一个数据帧内的变化可以忽略不计。 3.1抗多流干扰能力 当MIMO系统采用4根发射天线,5根接收天线,发送端均采用16QAM调制时,ML、迫零-串行干扰抵消 (ZeroForcing-SuccessiveInterferenceCancellation,ZF-SIC)算法和改进的广义球解码算法的误码率随信噪比变化的曲线如图1所示。从图1中可以看出,ZF-SIC性能最差,改进的广义球解码算法的性能与ML算法完全相同。 图1 改进的广义球解码算法和ML, ZF-SIC算法 图2 改进的广义球解码算法在不同初始半径下 的性能比较 的性能比较 3.2复杂度 将计算机完成一次加法、乘法和一次开方为一次运算[6],用浮点数来计算算法的复杂度。Fincke和Pohst证明了当d-1是矩阵G的特征值下界时,球解码算法的复杂度为[6]: (15) 式中,n为发射天线数;C为初始球半径。当d-1=C时,其复杂度近似为O(n6)。但是在n,d一定的情况下,C越大,复杂度越高。 假设完全信道估计下,一个采用2个发射机3个接收机的MIMO系统,发射机均采用64QAM调制。在信噪比相同时,改进的广义球解码算法2种不同初始半径的大小比较,具体分析如表1所示。 表1 改进的广义球解码算法在相同信噪比下2种初始半径的大小比较 从表1可以看出,信噪比在0~20dB时,C1 4结语 将球解码算法归结为在格点中搜索,结合LLL基约减算法[13]、Fincke-Pohst枚举法[4]以及广义球解码算法[5,6]的优缺点,提出了一种改进的广义球解码算法,该算法在2个方面进行了创新:一是引入一个置换矩阵;二是根据信噪比的特性来选取初始半径。通过仿真结果可以看出,改进的广义球解码算法在高信噪比的情况下,不仅性能在一定程度上有所改善,而且复杂度也相对较低。将该算法应用到MIMO-OFDM系统的信号检测是笔者下一步的研究内容。 [参考文献] [1]Yang H. A Road to Future Broadband Wireless Access: MIMO-OFDM-Based Air Interface [J]. IEEE Commun Mag, 2005, 43(1): 53~60. [2]Jankiraman M. Space-Time Codes and MIMO Systems [M]. London: Artech House, 2004. [3]Zheng L Z, David N, Tse C. Diversity and Multiplexing: A Fundamental Tradeoff in Multiple-Antenna Channels [J]. IEEE Trans Info Theory, 2003, 49: 1073~1096. [4]Fincke U, Pohst M. Improved Methods for Calculating Vectors of Short Length in a Lattice, Including a Complexity Analysis [J]. Math of Comput, 1985, 44: 463~471. [5]Damen G, Chleif A, Belfiore J. Lattice Code Decoder for Space-Time Codes [J]. IEEE Communication Letters, 2000, 4: 161~163. [6]Damen M O, Abed-Meraim K, Belfiore J C. A Generalized Sphere Decoder for Asymmetrical Space-time Communication Architecture [J]. Electron Lett, 2000, 36(2): 166~167. [7]Damen O, Gamal H E, Caire G. On Maximum Likelihood Detection and the Search for the Closest Lattice Point [J]. IEEE Trans Info Theory, 2003, 49(10): 2389~2402. [8]Agrell E, Eriksson T, Vardy A, et al. Closet Point Search in Lattices [J]. IEEE Trans Info Theory, 2002, 48: 2201~2214. [9]Pham D, Krishna R P, Peter K W, et al. An Improved Complex Sphere Decoder for v-blast Systems [J]. IEEE Signal Proc Letters, 2004, 11(9): 748~751. [10]Damen M O. Joint Coding/Decoding in a Multiple Access System, Application to Mobile Communications [D]. ENST de Paris,1999. [11]Yang Z K, Liu C, He J H. A New Approach for Fast Generalized Sphere Decoding in MIMO Systems [J]. IEEE Signal Processing Lett, 2005, 12(1): 41~44. [12]Conway J H, Sloane N J A. Sphere Packings, Lattices and Groups [M]. New York: Springer, 1999. [13]Lenstra A K, Lenstra H W, Lovsz L. Factoring Polynomials with Rational Coefficients [J]. Math Ann, 1982, 162: 513~534. [14]Varanasi M K. Decision Feedback Multiuser Detection: A Systematic Approach [J]. IEEE Trans Info Theory, 1999, 45: 219~240. [15]程云鹏. 矩阵论 [M] .西安: 西北工业出版社, 1999. [编辑]张涛 [文献标志码]A [文章编号]1673-1409(2016)01-0007-05 [中图分类号]TN929.5 [作者简介]杨梅(1983-),女,硕士,工程师,现主要从事电子技术基础和通信信号处理方面的研究工作;E-mail: yangmei@ahpu.edu.cn。 [基金项目]安徽省教育厅省级自然科学研究一般项目(TSKJ2014B03)。 [收稿日期]2015-10-28 [引著格式]杨梅,陈阳,李满华.一种基于MIMO系统的改进广义球解码算法[J].长江大学学报(自科版),2016,13(1):7~11.